大学数学专业高年级学生数学问题解决缄默知识获得的调查研究

杨泽忠，周海银

（1．山东师范大学 数学科学学院，山东 济南 250014；2．山东师范大学 教育学院，山东 济南 250014）

1 问题提出

数学问题解决过程中的缄默知识是指那些在数学问题解决过程中用于概括条件、分析问题、选择方法和恰当地调用以前学习过的数学知识来合理地解决当前问题的知识．这部分知识对于数学问题解决至关重要，但是，这部分知识由于具有非常强的非逻辑性和非公共性[1]，因此，在当前的数学教学中老师的教和学生的学都感到非常困难．老师的教感到困难是老师常常感到不能非常清楚地解释这些知识，学生的学感到困难是学生常常不能得其要领．因此数学问题解决过程中的缄默知识的教学已成为一个难点问题[2～4]．如何解决这个难点问题？当前说法很多，仁者见仁智者见智，至今也没有统一的观点[5～8]．深入研究一下那些在数学教学中能够听懂老师的讲解，能够理解老师所介绍的数学问题解决过程中缄默知识的同学——比如大学数学专业的学生——无疑是很有价值的，这也许能帮助我们直接找到解决上述问题的办法．为此，选择了山东省3所省属高等院校数学专业的学生进行了调查．

2 调查方法与过程

2.1 调查对象

山东省 3所省属高等院校数学专业大三和大四年级本科生314人．之所以选择数学专业大三、大四的学生进行调查，原因是这部分学生相比较数学专业低年级的学生和一般的中小学生在数学问题解决方面能力更强、水平更高，在平时的数学教学中获得的数学问题解决方面的缄默知识也更多．同时，他们对于数学问题解决中的缄默知识也有着比较好的理解和认识．

2.2 调查工具

采用在初步访谈基础上形成的自编问卷——初步访谈是在其中一所高校数学专业的大四学生中进行的．问卷根据访谈的结果将数学问题解决过程中常用的缄默知识分成了7大类和13小类，然后对每一小类分别设置了一个题目，这样共13个题目．对于每个题目又根据访谈结果给出了7个选项——6个确定的和一个开放性．这些选项可以多选，也可以单选．在回答时，要求学生不仅填写选项，而且还要把每个选项的贡献量写出来．调查问卷根据专家建议修订多次，最后达到了较高的效度．问卷信度经过重测研究达到0.91．

2.3 调查过程

调查问卷由主试和被调查对象的辅导员一起组织发放．采取自由答卷的方式，一天后交回问卷．调查共发放问卷 314份，全部回收，剔除无效卷后，其中有效卷为 294份，有效率为93.63%．

3 调查结果

3.1 总体情况

对于调查问卷给出的 13个题目学生的回答多种多样．在学生的回答中，6个固定选项均有学生选择，没有学生选择开放性的选项．总体选择次数最多的是第二个选项“通过看老师的解题演示学会的”（总体被选择 3 030次），最少的是第三选项“通过听同学和朋友的讲解学会的”（总体被选择 1 614次）．贡献量平均值最大的也是第二个选项（达到25.5%），最小的是第四个选项“通过看同学和朋友的解题演示学会的”（为6.26%）．大三同学和大四同学的选项情况虽有不同但差别并不明显．

3.2 关于理解数学问题方面缄默知识的获得

数学问题理解方面的缄默知识即是在阅读数学问题时如何理解其中的文字、图形、符号和公式等方面的知识．关于这部分知识的获得，有 85.71%同学选择第五个选项“通过自己看书（文字、图形等资料）学会的”，有75.51%的同学选择了第一个选项“通过听老师的语言说明学会的”．选择这两个选项的人数是最多的．不仅如此，根据学生的回答，这两个选项对于他们的理解数学问题方面缄默知识的获得的贡献也是最大的．这两个选项的贡献量分别占到了总体的39.18%和23.06%．所有同学的选项情况如图1所示．

由图1可以看出尽管选择其它选项的人数也不少，但其对于学生缄默知识获得的贡献量都不大，尤其是第三个选项“通过听同学和朋友的讲解学会的”和第四个选项“通过看同学和朋友的解题演示学会的”．

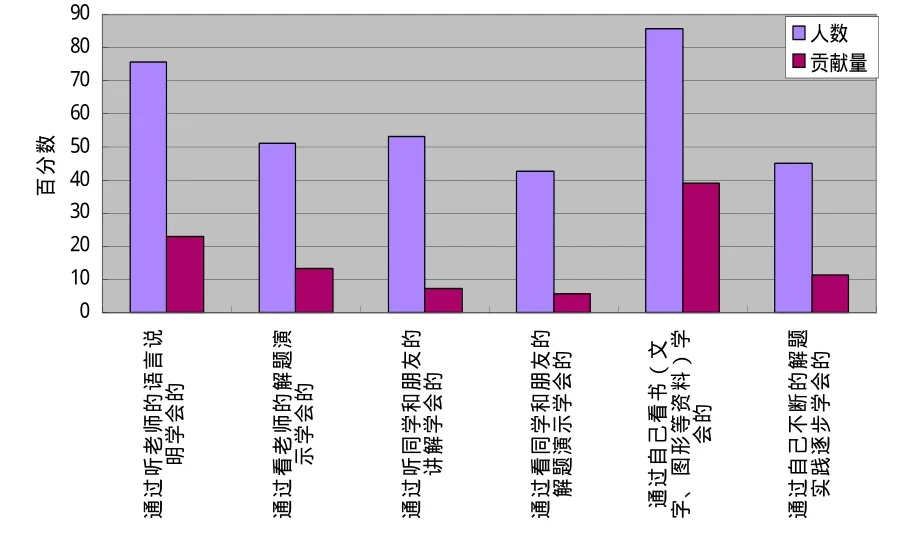
图1 学生对于阅读数学问题方面缄默知识获得的选项情况

3.3 关于整体把握数学问题方面缄默知识的获得

整体把握数学问题方面的缄默知识即是在理解了数学问题文字、图形和符号之后全面概括数学问题的内容，理解数学问题的主要意思，明确数学问题的条件、问题和关键点等方面的知识．这部分知识大体可分为两类，一类是概括问题方面的知识，一类是找出问题关键点方面的知识．对于第一类知识，有 87.76%的同学选择了第二个选项“通过看老师的解题演示学会的”，有 81.63%的同学选择了第五个选项．选择这个两个选项的人数是最高的．同时根据学生的反应，这两个选项对于他们缄默知识的获得贡献量也是最大的，分别达到了31.67%和23.33%．

对于第二类知识，有 87.76%的同学选择了第二个选项“通过看老师的解题演示学会的”，这个选项的选择比较集中．并且根据学生的反应，第二个选项对于他们缄默知识获得的贡献量也是最大的，达到了总体的41.9%．学生选项情况如表1所示．

表1 关于整体把握数学问题方面缄默知识的获得

由表1可以看出，除了上述几个选项，其它几个选项选择的人数都不是很多．但这里面比较特殊的一个是第一个选项．选择这个选项的的人数虽不是很多，但其对于学生缄默知识获得的贡献量却并不低．这也许是个值得注意的地方．

3.4 将数学问题与旧知识进行联系的缄默知识的获得

这部分知识又大体分为3类．第一类为发现数学问题与哪些旧知识有联系的知识，第二类为可将新问题归为哪类旧问题的知识，第三类为用旧知识恰当地表征新问题的知识．

对于第一类知识，有 85.71%的同学选择了第六个选项“通过自己不断的解题实践逐步学会的”．但根据学生的反应，此选项对于他们缄默知识获得的贡献量却不是最大的．最大的是第五个选项，其贡献量是 26.51%，其次才是第六个选项．学生选择情况如表2所示．

表2 将数学问题与旧知识进行联系的缄默知识的获得

由表2可以看出，对于第二类知识，有89.8%的同学选择了第二个选项，有 85.71%的同学选择了第六个选项．但贡献量最高的前二位却是第二个选项和第一个选项．对于第三类知识，有 89.8%的同学选择了第二个选项，有 83.67%的同学选择了第六个选项，有 79.59%的同学选择了第五个选项．但贡献量最高的前三位却是第二个选项、第六个选项和第一个选项．

3.5 寻找解题方法方面缄默知识的获得

这部分知识大体又分3部分，一是选择和提取旧知识应用于新问题方面的缄默知识，二是根据题目的特点和要求恰当的做辅助线、辅助函数等方面的缄默知识，三是寻找快速而简单的方法的缄默知识．对于这里的第一类知识，95.92%的同学选择了第一个选项，有 79.59%的同学选择了第二个选项．根据学生的反应，这两个选项对于他们缄默知识获得的贡献量也是最大的，分别是48.51%和17.71%．对于这里的第二部分知识，有 87.76%的同学选择了第二个选项，有85.71%的同学选择了第六个选项，有 83.67%的同学选择了第五个选项．并且这3个选项的贡献量也是最大的．对于这类的第三类知识，学生选择最多的是第二个选项和第五个选项，有 89.8%的同学选择了第二个选项，有 83.67%的同学选择了第五个选项．并且根据学生的反应，这两个选项的贡献量也是最大的．学生的选择情况如表3所示．

表3 寻找解题方法方面缄默知识的获得

3.6 问题解决过程中自我监控方面缄默知识的获得

问题解决过程中自我监控方面的缄默知识主要是指问题解决过程中解题者用于不断的调整自己的解题方向和方法，不断修正其中的错误和失误等的缄默知识．对于不断调整解题方向和方法方面缄默知识的获得，学生选择最多的是第五个选项，人数比例达到了 81.63%．学生选择第二多的是第二个选项，人数比例达到了 77.55%．但是，贡献量第一个大的却是第二个选项，第二大的才是第五个选项．对于不断修正自己的错误和失误方面缄默知识的获得，学生选择最多的是第二个选项，人数比例达到了 91.84%．并且，第二个选项的贡献量也是最大的．学生的选择情况如表 4所示．

表4 问题解决过程中自我监控方面缄默知识的获得

3.7 反思数学问题解决的缄默知识的获得

对于这部分知识的获得，多数学生选择的是第六个选项和第五个选项，人数比例分别达到了83.67%和73.47%．并且根据学生的反应，这两个选项对于学生缄默知识获得的贡献量也是最大的．学生的选择情况如图2所示．由图2可以看出，选择其它选项的人数虽不是很少，但其贡献量却明显偏低，特别是第四个选项．

图2 反思数学问题解决方面缄默知识获得的选项情况

3.8 解决实际问题方面缄默知识的获得

解决实际问题不仅要理解其中的数据和图形，而且还要理解相关的实践知识，不仅要用到一般数学问题解决的方法，而且有时候还要用到一些特殊的方法，另外，解决实际问题最后得到的结果不仅需要精确，有时候还要符合实际等．因此，解决实际问题的过程中也常常有一些缄默知识的运用．对于这些缄默知识，多数同学选择了第六个选项，人数比例达到了 85.71%．但根据学生的反应，对其缄默知识获得贡献最大的却是第五个选项，第五个选项选择的人数比例为69.39%．学生的选择情况如图3所示．

图3 解决实际问题方面缄默知识获得的选项情况

4 结 论

4.1 教学中老师关于数学问题解决过程的展示是学生获取关于问题解决缄默知识的重要来源和主要来源

由前面的调查结果可知，当问及学生其关于概括数学问题方面的缄默知识、找出数学问题关键点方面的缄默知识、将数学问题归类方面的缄默知识、用旧知识表征数学问题归类方面的缄默知识、提取旧知识用于数学问题解决方面的缄默知识、根据题目特点做辅助工作方面的缄默知识、选择快速而简单方法方面的缄默知识、调整解题方法方面的缄默知识和修正错误与失误方面的缄默知识这 9类缄默知识的来源时，绝大多数同学都选择了第二个选项“通过看老师的解题演示学会的”．并且，由学生给出每个选项的贡献量来看，第二个选项对于这九类缄默知识获得的贡献量几乎都在30%以上，有的甚至达到了47%．由此看出，教学中老师关于数学问题解决过程的展示给予了学生问题解决多方面的缄默知识，是学生数学问题解决中众多缄默知识的重要和主要来源．特别那些关于整体把握数学问题方面的缄默知识、将数学问题与旧知识进行联系方面的缄默知识、寻找解题方法方面的缄默知识和问题解决过程中自我监控方面的缄默知识等．

4.2 学生对数学问题解决的实践是学生获取问题解决缄默知识的另一重要来源

由前面的调查结果可知，当问及学生其发现数学问题与哪些旧知识联系方面的缄默知识、将数学问题归类方面的缄默知识、用旧知识表征数学问题归类方面的缄默知识、根据题目特点做辅助工作方面的缄默知识、反思数学问题解决方面的缄默知识和解决实际问题方面的缄默知识这 6类缄默知识的来源时，有大约84%的同学选择了第六个选项“通过自己不断的解题实践逐步学会的”．这个选项对于学生上述六类缄默知识获得的贡献量基本上都在 20%以上．由此看出，学生关于数学问题解决的实践是学生获得问题解决缄默知识又一个重要来源，特别是学生那些有关发现数学问题与哪些旧知识联系方面的缄默知识、反思数学问题解决方面的缄默知识和解决实际问题方面的缄默知识．这 3类缄默知识，实际上，由前面的结果可以看出，主要来源于学生关于数学问题解决的实践．因为在这3类缄默知识的获得上，选择第六个选项的人数都超过选择其它选项的人数，更远超选择第二个选项的人数．

4.3 学生对于数学问题解决相关知识的阅读理解也是其问题解决缄默知识获得的一个比较重要的来源

在上面的调查中，当问及学生其对于阅读数学问题方面的缄默知识、对于概括数学问题方面的缄默知识、根据题目特点做辅助工作方面的缄默知识、选择快速而简单方法方面的缄默知识、调整解题方法方面的缄默知识、反思数学问题解决方面的缄默知识和解决实际问题方面的缄默知识这 7类缄默知识的来源时，有75%左右的同学选择了第五个选项“通过自己看书（文字、图形等资料）学会的”．并且这个选项对于上述 7类缄默知识的贡献量也基本上都在 20%以上．由此看出，对于学生数学问题解决缄默知识来讲，其对于相关知识的阅读和理解也是一个比较重要的来源．其主要帮助了学生有关理解数学问题方面缄默知识的获得、有关寻找解题方法方面缄默知识的获得、有关反思数学问题解决的缄默知识的获得和有关解决实际问题方面缄默知识的获得．

4.4 学生的关于数学问题缄默知识有相当一部分也来源于老师在问题解决教学过程中的解释与说明

由上述调查结果可以看出，除了在问及学生关于选择和提取旧知识应用于新问题方面的缄默知识的来源时，有比较多的人选择了第一个选项，人数比例达到了 95.92%，对于其余的问题，选择第一个选项的人数都不是特别多．但是，对于每个问题选择第一个选项的人数也几乎都在 60%以上．并且根据学生的反应，第一个选项的贡献量几乎都在20%左右．因此，学生关于数学问题缄默知识的获得应该有平时教学中老师关于相关知识解释和说明的一份功劳，学生的关于数学问题的缄默知识中有相当一部分也应当来源于老师在问题解决教学过程中的解释与说明．

总之，由调查结果可以看出，日常教学中老师对于数学问题解决过程的展示、学生的数学问题解决实践、学生对于相关知识的阅读与理解和老师对于数学问题解决的解释说明是学生问题解决缄默知识获取的主要来源和重要来源．

5 思考和建议

缄默知识作为一种说不清道不明的知识，在教学中常常困难重重，原因在于其是难以编码的高度个人化的非公共知识[9～10]．鉴于此，波兰尼曾指出：缄默知识教学只能通过师傅带徒弟的方式进行，也就是由师傅操作、示范，徒弟观察、思考，然后再由徒弟模仿和总结的方式进行[11]．这种方式无疑是有效的，特别是在科学研究领域[12]．调查结果显示，数学教学中老师对于数学问题解决过程的展示与解释和学生的数学问题解决实践是学生数学问题解决缄默知识获得的主要来源和重要来源，似乎也契合了波兰尼的说法．

但是，在上述调查中也发现，有差不多一半的数学问题解决过程中的缄默知识主要来源于学生自己的学习，即学生对于相关知识的阅读和理解．在这部分知识的获得过程中虽然也有老师数学问题解决示范的影响，也有其它因素的作用，但学生对于相关知识的学习无疑起了关键作用和重要作用——否则不会有那么多学生选择第五个选项，第五个选项的贡献量也就不会那么高了．

由此看出，数学问题解决过程中缄默知识的获得方式有一般性，也有其特殊性．其一般性在于其与其它方面的缄默知识一样，学生在学习掌握的时候需要多看老师的示范，多听老师的解释，然后多模仿和多实践．其特殊性在于学生在学习这类缄默知识的时候，除了应采取的一般方法外，还需要多阅读相关的理论知识，从相应的理论知识中获取营养．

这样，在中小学数学教学中，为了使学生尽快掌握数学问题解决过程中的缄默知识，教师应：（1）改革常用的表演式的问题解决教学方式，使用师傅带徒弟一样的教学方法，多现场解题，使学生看到真实的问题解决过程．（2）问题解决教学过程中，特别重视数学问题解决的展示过程，即寻找机会多给学生展示问题解决的过程，给学生展示多种多样的数学问题解决过程，给学生展示全面而详细的问题解决过程等．（3）在给学生展示解题过程的时候，教师尽可能的把自己的思考过程和想法都告诉学生，以促进学生对问题解决的全面和深刻理解．（4）在问题解决教学中，教师应当注意指导学生仔细观察，深入思考，不断总结经验，然后在此基础上进行模仿、练习和多方面实践等．（5）教师应特别重视引导学生阅读与数学问题解决相关的知识，比如解题方法方面的知识，比如解题总结方面的知识，比如解题策略和技巧方面的知识等等，以促进学生关于数学问题解决缄默知识的全面获取和牢固掌握．

[1]波兰尼．缄默的认识[A]．瞿保奎．教育学文集——智育[C]．北京：人民教育出版社，1993．

[2]王延文，王光明．初中数学教育培养解决实际问题能力与创造能力的实验研究[J]．数学教育学报，1999，8（2）：72-75．

[3]王延文，齐建华，游安军．“问题解决”及其研究综述[J]．数学教育学报，1995，4（3）：35-39．

[4]王林全．问题解决的有关心理活动及其思考[J]．数学教育学报，2002，11（1）：36-38．

[5]石中英．缄默知识与教学改革[J]．北京师范大学学报（人文社会科学版），2001，（3）：101-108．

[6]黄晓学．缄默知识与数学教学改革[J]．徐州师范大学学报（自然科学版），2005，（1）：75-78．

[7]蒋茵．教师的缄默知识与课堂教学[J]．教育探索，2003，（9）：90-92．

[8]卢尚建．论教学中的缄默知识[J]．全球教育展望，2010，（1）：33-36．

[9]方明．缄默知识论[M]．合肥：安徽教育出版社，2004．

[10]李红梅．数学文化教育中教师的缄默知识探讨[J]．数学教育学报，2011，20（3）：19-21．

[11]波兰尼．个人知识[M]．贵阳：贵州人民出版社，2000．

[12]肖广岭．隐性知识、隐性认识和科学研究[J]．自然辩证法研究，1999，（8）：18-21．