基于录像分析背景下的优秀数学教师课堂提问能力的研究

叶立军，周芳丽

（1．杭州师范大学 理学院，浙江 杭州 310018；2．杭州经济技术开发区学正小学，浙江 杭州 310018）

1 研究背景

随着基础教育课程改革不断深入，如何有效地开展课堂教学活动进而提高课堂教学效率已经成为人们关注的热点话题．实际上，数学的多数活动与教学评价的许多程序，都是以提问为中心的．教师的课堂提问行为是课堂教学的重要一环，浓缩了教师对课堂和学生的理解，浓缩了课堂教学的艺术．而优质的提问类型和策略亦是优质教学的核心和关键，在一个充满优质问题和优质提问方式的课堂气氛中，能让学生意识到一种对他们学习所具有的共享责任感[1]．一位成功的教师总会把握这些时机，发挥提问的艺术，开启学生思维的闸门，激发学生学习的兴趣，保证教学活动顺利、高效地进行．当观察这些成功的教师时，会注意到他们在课堂上的问题似乎遵循一个特定的模式或顺序，以及他们提问或问题表达的方式也有一定的特点[2]．从一定程度上讲，教师的提问能力决定着课堂教学质量的高低[3]．文章通过录像分析探究优秀教师数学教学提问能力及其课堂教学的关系．

2 研究方法

2.1 研究目的

利用同课异构的方式，通过录像分析的方式记录两堂“合并同类项”课的教学实录，反复观看录像，对教师教学提问类型、方式以及所引发的学生的回答方式进行分类和统计，并对其进行编码分析，从而探究优秀教师数学教学提问能力以及优秀教师教学与学生参与[4]之间的关系．

2.2 被试选取

研究主要对优秀教师这一概念进行界定．借鉴已有的界定方法，采用3项标准作为斟选优秀教师的依据：一是从事教学15年以上的教师，二是具备高级职称或获得教学荣誉的教师，三是在所任教的学校有着良好的教学业绩和教学口碑的教师．

选取两名浙江省数学教学名师作为研究对象，教师 A的教龄为30年；教师B的教龄为26年，两名教师的职称都是中学高级教师，而且都是浙江省特级教师．根据界定优秀教师的标准，两位教师均符合优秀教师标准．两名老师所授课的班级都来自杭州某学校七年级两个班的学生，这些班级学生在组班之初都是由电脑随机抽选组班，因此班级学生成绩及学生素质没有太大差异．

2.3 研究材料

研究的教学内容是浙教版七年级上册“4.5合并同类项”，在这节课之前，学生已经学习了有关代数式的一些基本知识，如用字母表示数、代数式的值和整式．在此节课之后，学生将学习“4.6整式的加减”．“合并同类项”内容不仅在该章的学习中起到重要的承上启下作用，同时也是培养学生分类、抽象概括能力的重要内容[5]．

2.4 研究工具

在借鉴TIMSS Video Study的录像编码和视频案例研究后，采用了录像分析的研究方法．

3 研究过程

3.1 教师提问类型及其等候时间的编码

对每一堂课、教师每个提问类型及其所引发的学生不同的回答方式进行统计比较，其中包括对教师在不同的教学环节中各类提问类型的次数，占总提问的百分比，以及根据提问类型的不同，从而区别优秀教师对不同的提问类型所引发学生不同的回答方式的差异．

根据提问作用以及认知水平的不同层次，在 Bloom认知领域分类的6个层次：识记、理解、应用、分析、综合和评价的基础上，结合课堂实录中数学教师提问作用和目的，将Bloom的6个层次拓展为：识记、管理、提示、重复、理解和评价等6种类型[6]．

根据教师提问后所涉及的等候时间[7]，将教师提问后的等候时间归为5类：“停顿不足3秒”，“停顿3～5秒”，“停顿6秒以上”．

为了探究教师提问方式与提问后等待时间的长短是否存在相关性，将教师提问方式和等待时间看作两个变量，根据教师提问后等待时间的长短和提问认知程度不同，将 3类等待时间和6种提问类型分别赋值．

定义提问类型赋值：随着教师提问认知程度的增加，依次将教师提问类型赋值，管理性提问记为1分，识记性提问记为2分，重复性提问记为3分，提示性提问记为4分，理解性提问记为5分，评价性提问记为6分．

定义等待时间赋值：随着教师提问后等待时间的增加，给学生思考和参与机会的增多，依次将教师提问的等待时间赋值，停顿不足3秒记为1分，停顿3～5秒记为2分，停顿6秒以上记为3分．

3.2 学生回答方式的统计

根据教师所提的不同类型问题而引发学生的不同应答方式，将应答方式分为：指定某个学生回答，指定某个小组回答，全班或部分学生回答、指定多位学生回答，学生自发回答等5种类型[8]．

（1）指定某个学生回答：教师在提问前或者提出问题后，指定某一位学生作答．

（2）指定某个小组回答：教师在提问前或者提出问题后，指定某个小组的学生作答．

（3）全班或部分学生回答：教师向全班学生提问，回答时由学生自行决定是否作答．

（4）指定多位学生回答：教师在提出某个问题后，先后指定多位同学对这一问题进行回答．

（5）学生自发回答：教师在提出问题后，未指定任何学生作答，学生自发的进行作答．

4 研究结论及启示

（1）在数学课堂教学中，优秀教师在不同的教学环节所采用的提问数量和提问类型各不相同，其中以讲解新知和练习讲解环节提问的数量最多．

研究发现，两位优秀教师的课堂教学基本包括引入新课、讲解新知、例题讲解、练习讲解、小结（含点评）等环节，并且提问始终贯穿于整个教学活动中．研究者对两位优秀教师的各个课堂教学环节中的提问类型进行分类统计后发现：虽然，教师A和教师B（表中分别记为TA和TB）使用各种提问类型的次数不同，各个环节所用的各种提问类型也不尽相同，但在各个教学环节中，两位优秀教师使用各类提问情况的总体差异性并不显著．

从表1可以看出，两位教师在讲解新知和练习讲解环节提问的数量最多，是其它教学环节的3—4倍，也就是说优秀教师特别注重知识的探究和巩固．优秀教师善于根据不同的教学环节提出符合学生认知的问题，提高学生的参与度．而且两位教师在整堂课中提示性提问和理解性提问用的较多，也就是说在整个教学环节中，中国优秀数学教师善于让学生结合所学知识进行一定的思考、归纳和总结，并且根据学生回答问题的情况，进一步提出相应的问题，启发学生进一步思考．还会根据不同的教学环节、教学内容、所期望的知识水平、学习需要和兴趣来构建不同层次的提问策略．从所有教学环节中的各类提问数量分布来看，优秀教师对各种提问策略的使用也比较保守．

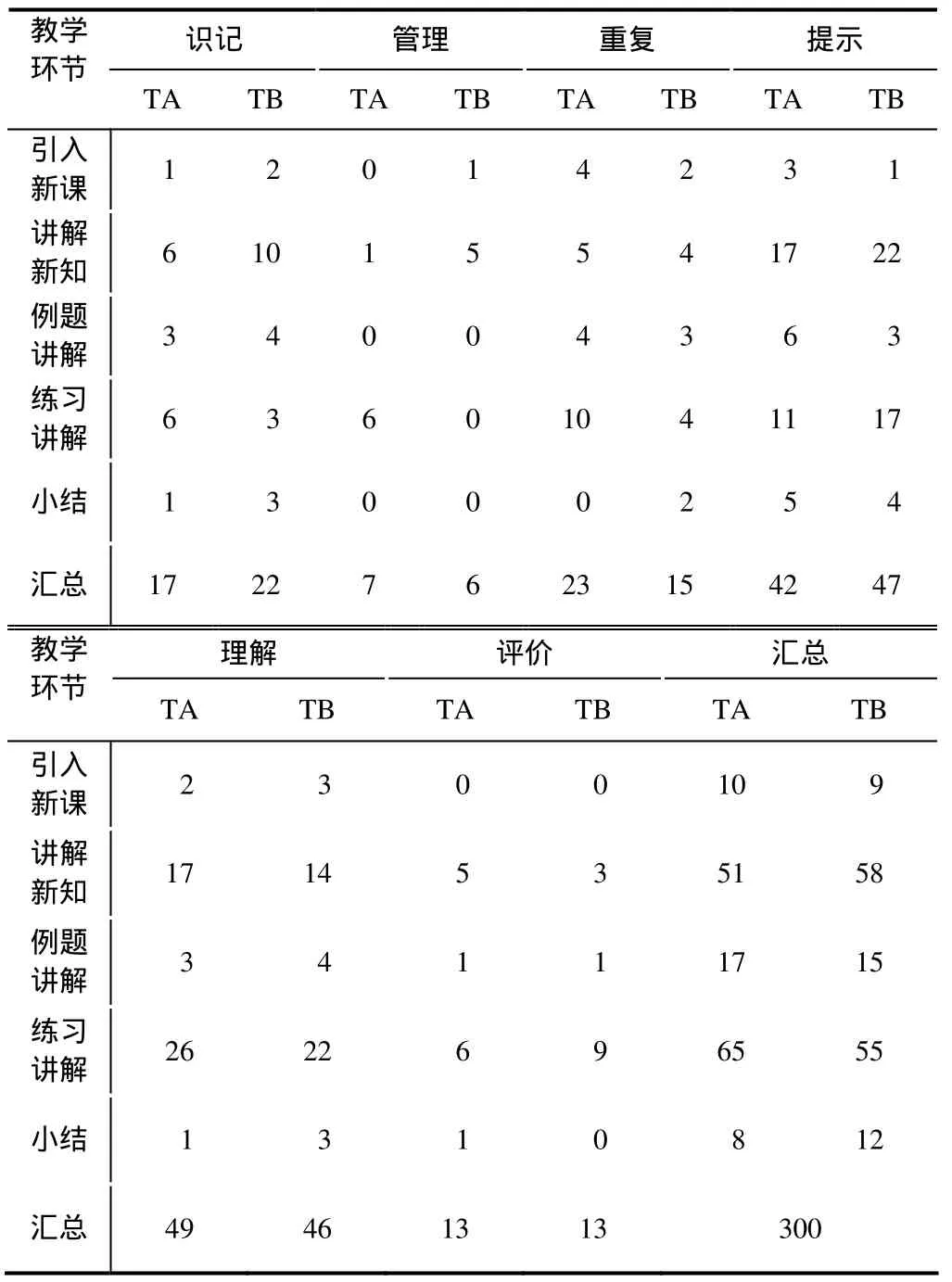
表1 两位教师在各教学环节中各类提问的数量分布

（2）从教师的提问方式上看，优秀教师善于采用大量追问，使用问题形成高效的“问题链”以提高课堂效率．

教师作为课堂教学的主导者和组织者，通常在与学生的一问一答，一问一思中把学生引向学习的内容，把学生引向问题的关键处、实质处，因此数学课堂追问是激发学生积极思维的动力；是开启学生智慧之门的钥匙；是信息输出与反馈的桥梁；是沟通师生思想认识和产生情感共鸣的纽带[9]．从表2可以看出教师A和教师B都使用了大量的追问，其中追问所占总提问数量的比例分别为35.8%和32.2%，而且参与发言的学生也占了一定的比例．优秀教师正是利用一个个“有意义的切入点”，合理地采用追问，充分发挥课堂追问的效能提高学生的参与度，激发学生的思维来传授重要内容．

表2 追问与学生参与统计表

优秀教师还具有较强的预设能力，预期到一个问题会使学生开始进行的某种智力活动，更具有较高的应变能力和思维能力，通过合理的追问引导学生积极反思，善于根据学生的回答来把握课堂教学中的问题，提高学生的参与度．

（3）优秀教师善于针对不同类型的问题引导学生采取不同的回答方式，激发学生高认知的思维．

根据6种提问类型的提问难度的不同，将教师提问分为“简单性提问”、“半简单性提问”和“复杂性提问”．简单提问包括：管理性提问、识记性提问；半简单性提问包括：重复性提问和提示性提问；复杂性提问包括理解性提问和评价性提问．

根据教师对学生5类应答方式控制水平的不同程度，将学生回答的方式归为“控制”、“部分控制”和“自由”．控制包括：指定某个学生回答和指定某个小组回答；部分控制包括：全班或部分学生回答和指定多位学生回答；自由是指学生自发回答[8]．

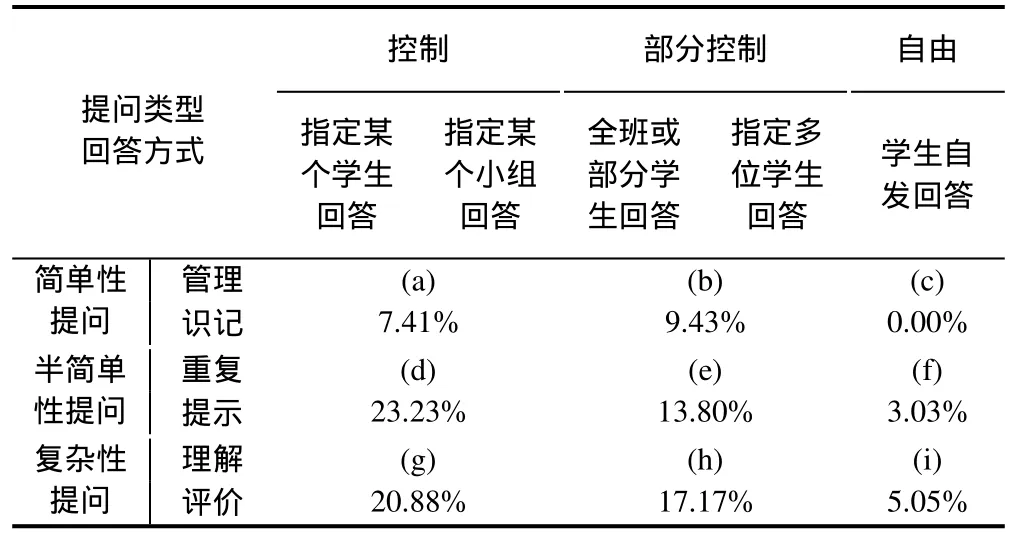
表3 师生问答情况归类分析表

研究者对师生的问答情况进行统计分析，根据教师控制回答的程度和智力激发的程度两个维度来分析优秀教师的行为倾向，从而定量地描述师生间的对话教学．从表3可以看出，两位优秀教师在（d）格和（g）格的行为所占比例较高，分别是23.23%和20.88%，其次是（h）格和（e）格的行为，分别是17.17%和13.80%，而在（c）格、（f）格和（i）格的行为所占比例较少，说明优秀教师能够很好地驾驭课堂，倾向于严格调控课堂秩序并提出半简单性问题与复杂性问题，激发学生较高认知程度的思维．对于部分复杂性的提问和半简单性提问，优秀教师也会给予学生足够的自由，鼓励并启发学生从高认知水平上回答．

随着优秀教师有针对性、高水平的提问能力，引导学生们专注、有效地思考，学生们便不再去思考他能够或被迫回答可以抵抗老师的意志、不回答问题等无效的时间，那么他就能更好的集中精力思考和学习，更好的参与到教学中来，从而创造高认知的回答[10～11]．

（4）从教师提问的策略来看，优秀教师善于针对不同的提问类型采用不同的等候策略，调动学生的思维活动，提高学生的参与度．

通过对两节课中教师提问类型和提问后的等候时间进行统计和分析，研究者发现优秀教师对不同的提问类型采用不同的等候策略，然后利用SPSS软件根据其赋值情况分别对教师A和教师B的提问类型和等候策略进行Pearson相关性分析，最后再将两节课所有提问类型和等候策略统一在一起作两个变量的Pearson相关分析，得到如下结果（如表4）：

表4 相关性分析

从表4中可以看出Sig.（2-tailed）双尾t检验值<0.05，说明两者存在显著相关关系，即两位优秀教师的提问类型与提问后等待时间的长短之间存在明显的线性关系．也就是说，教师对不同类型的问题采用不同的等候策略，对低认知水平的问题，等候的时间较短，不足3秒；对一些高认知水平的问题，等候的时间相对较长，超过6秒甚至10秒以上，这给予了学生充分的思考时间，提高学生对问题的理解层次．总而言之，优秀教师在提出问题后，善于根据不同难度的问题所引发学生的认知程度的不同，留给学生不同的思考时间，从而充分调动学生的思维活动，提高学生的思维水平和学生的参与度．

教师只有在提出的问题难易程度适当，处于学生的“最近发展区”，使学生的心理特征处于“愤”、“启”的状态，他们的思维才能最大限度地活跃起来．等待时间只有长短适中，才能既有足够的时间调动学生思维，又不至于因时间过长而在思维完成后无事可做．

[1]Jackie Acree Walsh．优质提问教学法[M]．北京：中国轻工业出版社，2009．

[2]伊凡·汉耐尔．高效提问——建构批判性思维技能的七步法[M]．汕头：汕头大学出版社，2003．

[3]白改平，韩龙淑．专家型—熟手型数学教师课堂提问能力的个案比较研究[J]．数学教育学报，2011，20（4）：16-19．

[4]斯海霞，叶立军．基于视频案例下初中数学课堂学生参与度分析[J]．数学教育学报，2011，20（4）：10-12．

[5]斯海霞，叶立军．新老教师数学抽象概括教学差异的比较研究[J]．数学教育学报，2010，19（6）：53-55．

[6]叶立军，胡琴竹，斯海霞．录像分析背景下的代数课堂教学提问研究[J]．数学教育学报，2010，19（3）：32-34．

[7]王运庆，叶立军．基于录像分析背景下数学课堂教学中“等待时间”的探析[J]．新课程研究，2010，（3）：108-110．

[8]柳夕浪．课堂教学临床指导[M]．北京：人民教育出版社，2003．

[9]孙琪斌．课堂提问统计表的设计与应用[J]．上海教育科研，2008，（2）：68-69．

[10]Wigle Stanley E. Higher Quality Questioning [J]. Education Digest, 2002, 65(4): 62-64.

[11]叶立军，斯海霞．基于录像分析背景下的代数课堂教学语言研究——以两堂《分式的乘除》课堂实录为例[J]．数学教育学报，2011，20（1）：42-44．