永磁电机在额定负载时转子温度场分析

辛建军

(牡丹江大学，黑龙江牡丹江 157011)

为了校核数值计算结果的准确性，本研究将采用具体的试验来测量电动机转子槽楔、铁心、铜片以及永磁体的温度，电动机温度的测量点分别如图1所示。

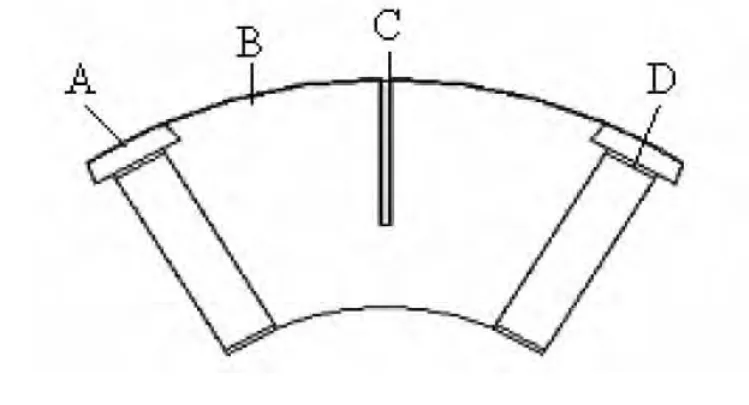
图1 电机温度的测量位置

利用确定永磁电动机电磁损耗的基本方法，在电机损耗准确计算的基础上，把所得的热源代入温度场求解程序，并采用有限元法计算电机额定负载运行时的稳态温度分布。在试验过程中，由于D点传感器故障，故未给出测量值。其余各测量点温度的计算值和实验值的比较如表1所列。此时，电动机试验环境的温度为27℃。

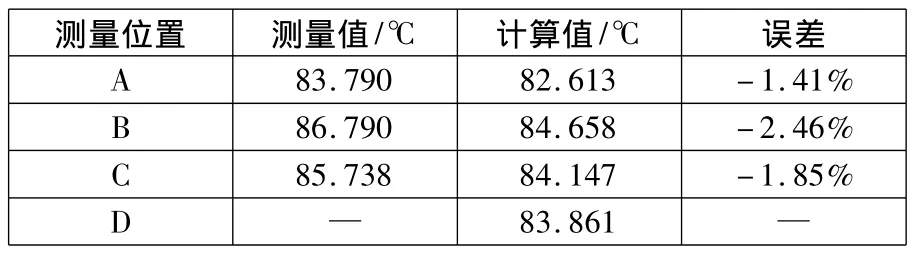
表1 温度场计算与实测结果对比

从表1可以看出，在电动机的不同温度测量位置，温度场的计算结果和实验结果比较一致，完全能够满足工程计算的要求，并且验证了转子附加损耗计算和温度场模型的准确性和工程实用性。图2为求解域的温度分布。

从图2中可以看出:

1.电动机转子温度沿着周向呈对称分布。这是由电动机的结构形成的结果，在求解域的确定过程中，由基本假设可知电动机的结构式对称的方式。

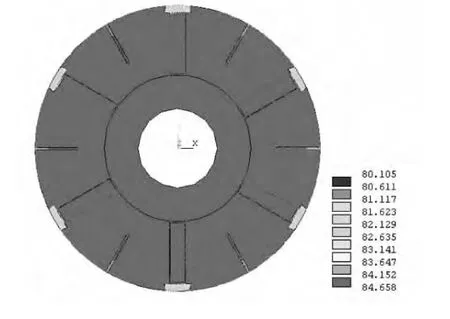
图2 求解域的温度分布(℃)

2.最高点位于铁心，其温度数值为84℃左右;槽楔处温度最低，其数值结果为80℃左右，且转子内部温差较小。由于电动机转子一个封闭的区域内运行，转子的散热仅仅依靠转子的旋转在其表面所产生的对流效应进行，而此散热系数数值较小。温度高低部分的结果则是由于电机损耗分布的特性造成。

3.从计算数值结果与实验结果的比较来看，二维温度场的数值计算结果与实际温度趋势一致，能如实反映转子各部分的温度分布。

为了进一步考察永磁电动机转子温度场的分布特性，将电动机的转子局部温度分布分别提取出来，电动机的铁心、铜片、永磁体以及槽楔等局部温度分布分别如图3、4所示。

从图3中可以看出，最高温度出现在转子铁心表面，这是由于转子附加损耗主要集中在铁心表面的缘故。由于与槽楔接触，靠近槽楔处铁心温度逐渐降低。铜片与铁心接触面积较大，而且各自的导热系数很大，故铜片与铁心温差较小。由于与气隙对流换热的影响，铜片靠近转子表面一端温度较低，随着埋入转子深度加深，温度增加。从图4可以看出，最低温度出现在槽楔处，与实验结果相吻合。永磁体上表面与槽楔接触，温度稍低。其余部分与铁心紧密结合，故而接近铁心温度。

图3 铁心和铜片的温度分布(℃)

图4 永磁体和槽楔的温度分布(℃)

1.不带风扇运行时温度场分析。

永磁材料的磁性能与永磁电机的运行性能密切相关。本文多研究的永磁电动机采用的永磁体材料为钕铁硼，它的允许工作温度为150℃。由于钕铁硼的温度系数很高，造成其磁性能热稳定性较差，因而在高温工作时可能造成不可逆退磁。为了更大限度地分析电动机的热性能，本文研究了电机不带风扇运行时，转子各部分特别是永磁体的温升情况。表2为电机不带风扇运行时，各测量点温度的计算值和实验值的对比情况，环境温度为27℃。

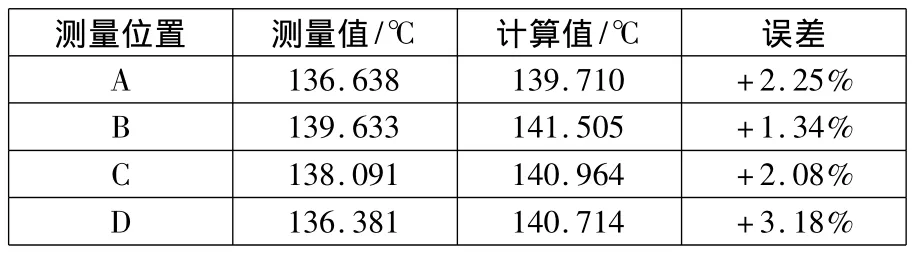
表2 温度场计算与实测结果对比

通过对以上数值计结果的分析研究可以看出:

(1)温度场的计算结果和实验结果较好吻合;

(2)由于电机不带风扇运行，机壳表面散热较慢，间接导致气隙温度升高，因此此时转子各部分温度较带风扇时显著升高;

(3)电动机永磁体实测温度为136.4℃，低于其允许工作温度，说明电机不带风扇运行时，永磁体仍然不会产生不可逆退磁，电机仍然可以正常工作。

图5为电动机不带风扇运行时求解域的温度分布，而图6、7为不带风扇运行时电动机转子局部温度分布情况。

将在此情况下的温度场数值计算的相应结果图5、6、7与以上计算的结果图2、3、4进行对比可知:该永磁电动机转子二维温度场的整体以及转子各部分的温度分布趋势以及规律与电动机带风扇运行时相一致，最高温度均出现在转子铁心部位，而电动机的最低温度均出现在转子的槽楔位置处。

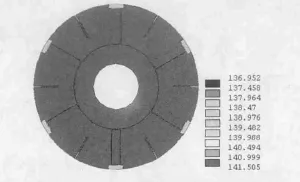
图5 求解域的温度分布(℃)

图6 铁心和铜片的温度分布(℃)

图7 永磁体和槽楔的温度分布(℃)

2.附加损耗对转子温度场的影响。

在本论文的研究中，为了进一步研究附加损耗对转子温度场的影响情况，在保持电机结构恒定不变的条件下，通过改变铁心材料参数来改变转子表面附加损耗，进而分析附加损耗的变化对转子温度分布的影响。

分别取附加损耗为电机额定负载时附加损耗的倍，对铁心和永磁体的最高温度分布进行研究。图8给出了电机转子温度随附加损耗的变化曲线，环境温度为27℃。

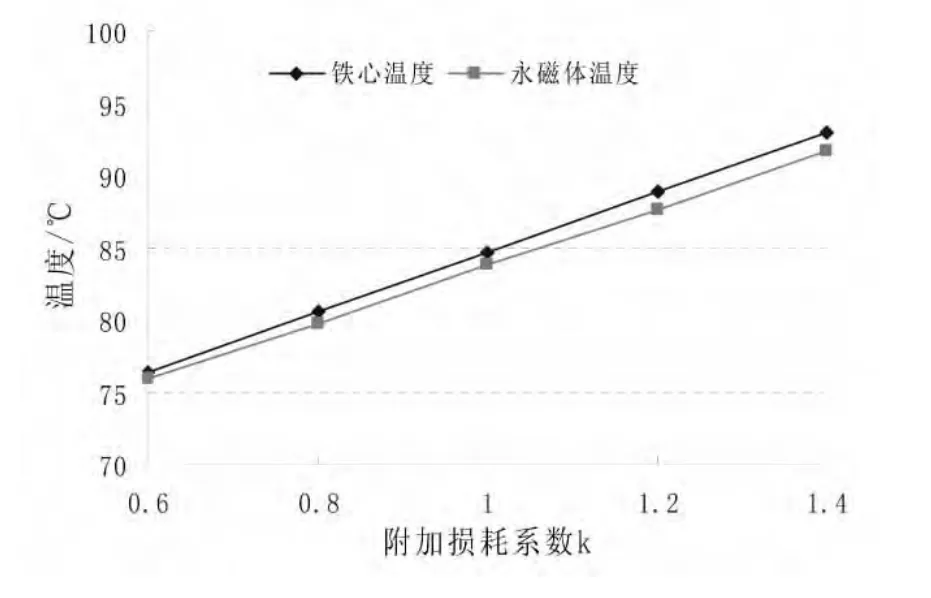
图8 附加损耗对转子温度场的影响

通过对图8的分析研究可以看出，附加损耗对转子温度影响显著，永磁体温度和铁心温度接近，且与附加损耗近似成线性变化。

综上，根据永磁电动机的结构特点，在基本假设的基础上，建立了永磁电动机转子二维温度场求解模型。通过温度场微分方程的建立以及各类边界条件的给定，特别是相应的损耗、散热系数的确定。采用有限元法对永磁电动机转子二维温度场进行了数值求解，并将数值计算结果和实验数据进行了对比研究，佐证了本论文所采用的研究方法的合理性以及求解域确定的正确性。

［1］张新波，许承千.电机三维温度场的综合分析［J］.电工技术杂志，2000(3):4～6.

［2］裴远航.汽轮发电机定子温升分布的三维有限元分析［J］.大电机技术，1992(5):24～28，31.

［3］张大为，汤蕴璆，等.大型水轮发电机定子最热段三维温度场的有限元计算［J］.哈尔滨电工学院学报，1992(3):186～194.

［4］孔祥春，付敏.水轮发电机转子中部最热段三维温度场的有限元计算［J］.哈尔滨理工大学学报，1996，1(1):53～59.