局部连续场下重力辅助导航模型构建算法

文超斌，王跃钢田 琦郭志斌左朝阳杨家胜

（1.第二炮兵工程大学 304教研室，西安 710025；2.中国人民解放军96124部队，通化 134000）

局部连续场下重力辅助导航模型构建算法

文超斌1，2，王跃钢1，田 琦1，郭志斌1，左朝阳1，杨家胜1

（1.第二炮兵工程大学 304教研室，西安 710025；2.中国人民解放军96124部队，通化 134000）

为了研究高精度的重力辅助导航模型以克服传统模型的局限，必须建立精度高且具有良好解析性质的局部重力异常场解析模型，同时考虑模型误差方程中的重力精准补偿问题。针对二维高斯样条函数逼近局部重力异常场中的局部支撑参数选择问题，通过对所涉及的系数矩阵、解误差、插值模型精度评估等问题进行分析，提出了一种新的最优局部支撑参数计算方法；基于此提出了一种高精度的基于高斯插值的重力辅助导航模型构建算法，该精准模型补偿了重力扰动矢量、标准重力值误差、厄特弗斯修正计算值对导航模型的影响。实验结果表明利用新型重力辅助导航模型构建算法，可使辅助导航系统位置精度提高1倍左右，姿态、速度精度提高1～2倍，定位误差保持在100～200 m。

重力辅助导航；高斯样条插值；重力误差补偿；导航模型

重力匹配辅助惯性导航作为一种利用地球重力场特征信息结合匹配算法对对惯性导航系统位置信息进行初次估计，而后采用导航数学模型方程结合一定的滤波算法对惯性导航系统位置信息进行进一步精准修正的新技术，近年来得到了快速的发展。目前关于重力匹配算法的研究文献较多，按照匹配算法设计原理可分为序列相关匹配方法和递推滤波方法两种，序列相关匹配方法主要包括最近等值线迭代算法（ICCP），相关极值分析算法两大类[1-5]；获取高精度、高分辨率重力异常图是进行准确匹配的关键所在。高斯样条函数具有局部支撑的良好特性，用其作为样条基函数对计算区域重力异常进行二维整体逼近，能在保证重力异常局部特性不失真的前提下获取计算区域重力异常的统一解析式等优点，近年来有关学者进行了相关应用研究。但针对该问题中涉及到的局部支撑参数计算问题分析并不多，局部支撑参数过大或过小都将导致很大的逼近误差，太大或太小均失去插值意义，有必要对其进行寻优，研究相应的寻优算法[6-7]。

目前重力辅助导航系统状态方程建模中通过地球正常重力模型得到的正常重力矢量进行重力补偿，未考虑重力异常扰动矢量、标准重力值误差（标准重力值误差由测量位置维度误差解算引起）和厄特弗斯修正计算值三类误差影响，这些误差都将引起带来导航误差，随着惯性元件精度的不断提高，惯性元件带来的系统误差与上述三类误差带来的系统误差处在同一个量级，系统误差不能被忽略，有必要采用精度更高的重力辅助导航系统状态方程模型对正常重力矢量进行补偿[8-12]。

所以，本文首先针对二维高斯样条函数逼近局部重力异常场中的局部支撑参数选择问题，通过对所涉及的插值系数矩阵可逆性进行研究给出了局部支撑参数的上限值，而后通过对插值系数矩阵解误差研究，给出了矩阵条件数和局部支撑参数定性关系，最后结合插值模型精度评估理论，提出了一种新的高斯基插值函数最优局部支撑参数计算方法，接着局部连续重力异常场提出了一种考虑重力扰动矢量、标准重力值误差、厄特弗斯修正计算值的精准重力辅助导航模型构建算法，最终为重力辅助惯性导航理论的高精度实践化应用打基础。

1 高斯基插值函数最优局部支撑参数计算

1.1 二维高斯样条优化插值数学模型

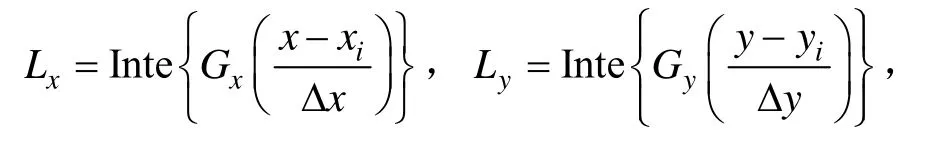
式中，Δx、Δy为格网点分辨率[7]。这样符合上述条件的xy平面二维高斯基函数可写成矩阵形式：

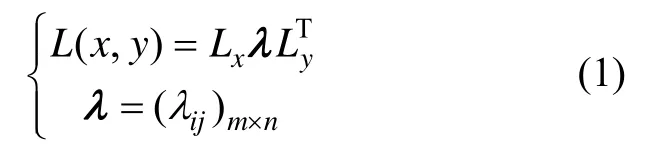
插值条件：

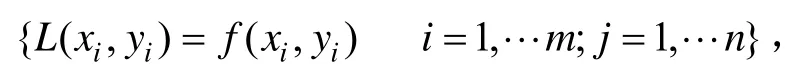
将矩阵组合则有如下线性方程成立：

可见，高斯基插值函数存在两个重要参数需要确定，第一：插值系数矩阵λ；第二：局部支撑参数a。如果X、Y均为非奇异矩阵，则式(2)有唯一解，将插值系数矩阵λ代入式(1)便得到该局部重力异常基准图二维高斯基函数逼近解析式；局部支撑参数参数a决定了X、Y矩阵求逆的具体求逆误差，应赋予局部支撑参数a值，使矩阵X、Y求逆误差较小；当a过小时，由于局部支撑区间很小，使得插值曲线刚度小，容易出现锯齿状；当a过大时，由于局部支撑区间很大，插值曲线刚度大，插值曲线过于平滑甚至使插值解析式在已知点的插值误差很大，所以a太大或太小均失去插值意义，因此有必要对参数a进行寻优，结合插值模型精度评估方法进行解算获取参数a的最优值。

1.2 插值系数矩阵可逆性和求逆误差

1.2.1 插值系数矩阵可逆性研究

设上述式(2)中高斯对称矩阵阶数K，如下示：

上述系数矩阵记为Ψ，考虑Ψ在什么条件下满足非奇异，由数值计算方法理论知只要该矩阵是严格对

角占优即可。也就是对于第i行，：

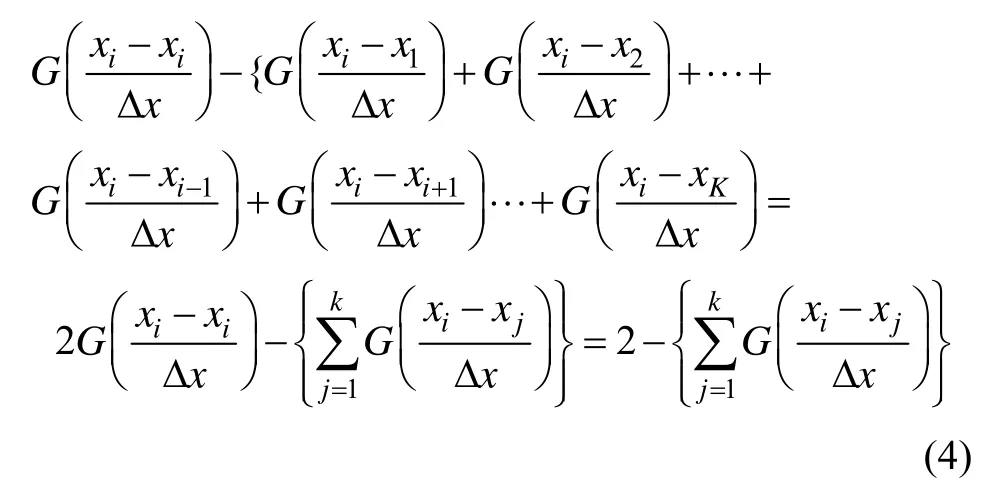
严格对角占优：

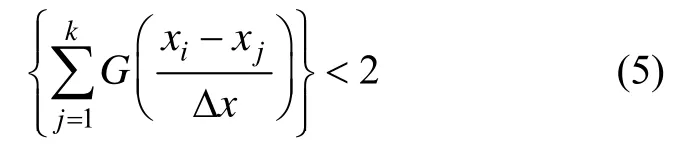
成立，上述式(5)左边可放大为：

所以只要确保式(7)成立则可以保证系数矩阵Ψ非奇异，对曲线的高斯插值总是可以保证的。可见a值最大限度为。

1.2.2 求逆矩阵误差研究

对于矩阵Ψ，设为定向量空间nR上的向量范数，矩阵范数由式(8)给出：

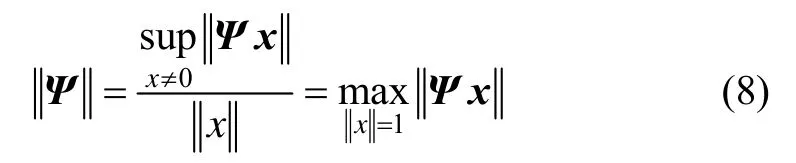
可逆矩阵Ψ的条件数由式(9)给出：

由于计算机计算系数矩阵Ψ时，每个元素存在计算误差，于是设扰动矩阵为E，则存在如下引理：

引理1：如果对任意满足的扰动矩阵E和一个与E无关的正常数δ，矩阵Ψ的条件数由：给出，对于方程Ψx=b和解x和y，式(10)成立，则。

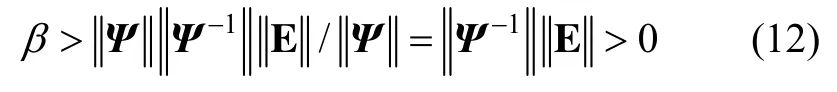
又由式(11)知：2/(1-β)＞1，所以0＜β＜1。于是当β单调增时，1-β单调减小，2(1-β)单调增，单调增。所以当时，此时对应的值就是方程的解x和y的最小的相对误差上界。于是有以下定理结论：

定理1：如果对任意满足的扰动矩阵E，矩阵Ψ的条件数由：给出，方程的解x和y，于是关于矩阵Ψ、E、x、y存在如下不等式：

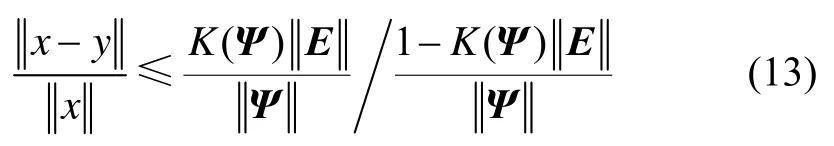
定理1说明在误差估计式(13)中，用求逆条件数可以得到最小的相对误差上界。该等式给出了矩阵扰动相对误差和由扰动引起的矩阵方程解相对误差值间关系。

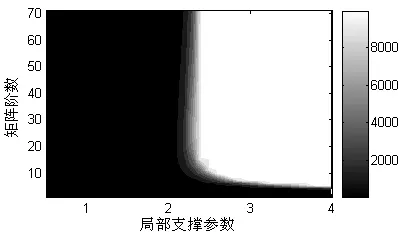
图1 Ψ矩阵的条件数分析图Fig.1 The condition number analysis of Ψ

1.3 插值模型精度评估

对局部支撑参数a进行寻优，为了保证插值函数与已知数据点保形性良好，同时考虑更多的函数非线性变化因素，研究利用分段二次抛物线代替所求插值函数对应的准确值，寻求分段二次抛物线与插值函数距离最小时对应的局部支撑参数amin，同时将二维局部重力异常基准图问题解耦为x方向一维高斯基函数和y方向一维高斯基函数分别构造进行寻优建模。求解其对应的x方向最优局部支撑参数axmin，y方向最优局部支撑参数aymin，由此选择可使插值函数与已知点具有最好的保形性，差值误差较小。

具体建模方法为：对n行格网点，每行分别进行上述二维高斯插值局部支撑参数的寻优建模，而后利用所有寻优建模准则函数之和作为二维高斯样条函数插值x方向的寻优模型，局部支撑优化函数(Local Support Optimize Function)LSOF寻优模型如式(15)示；对m列格网点，同x方向的寻优处理方法，LSOF如式(17)示，于是将局部支撑参数a限定在[0.2，2.5]区间内，分别按照式(15)(17)寻优准则进行计算，即可得到最优化局部支撑参数。

式中，ai，j、bi，j、ci，j为方程组(16)的解：

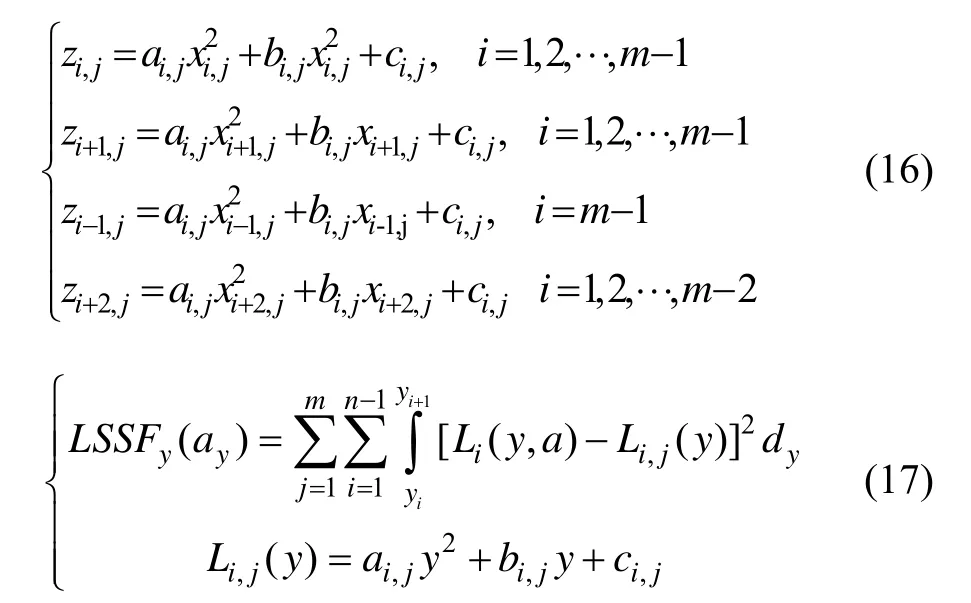
其中，ai，j、bi，j、ci，j为方程组(18)的解，

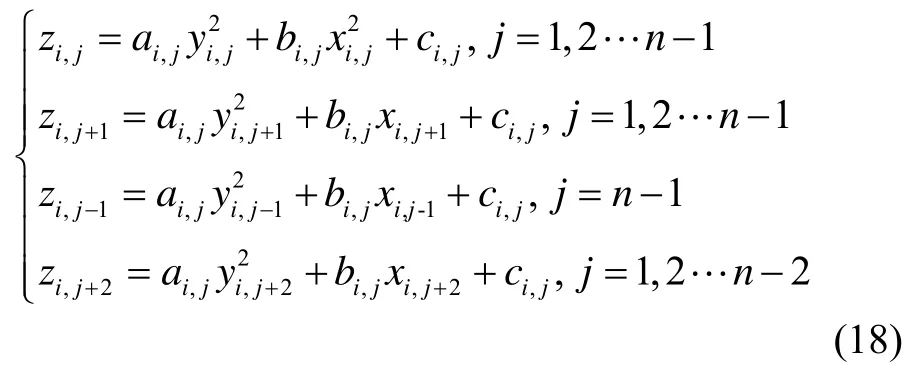
2 精准重力辅助导航模型构建算法

2.1 速度误差精准模型方程

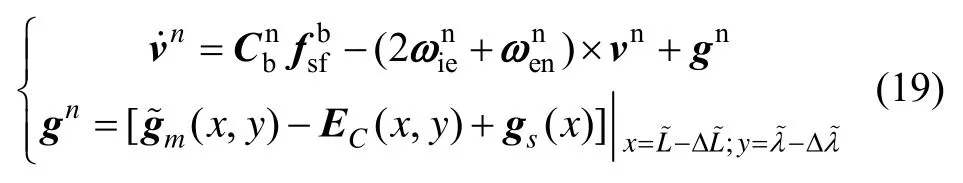
实际系统中总存在各种误差，所以实际系统中考虑各种误差情况下，实际速度计算值应由下述方程确定：

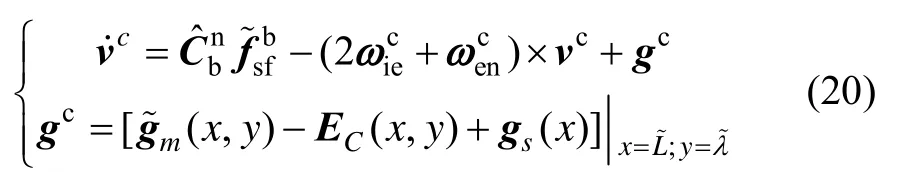
用式(20)减去式(19)，略去二阶小量可得线性近似的捷联惯导误差方程为：

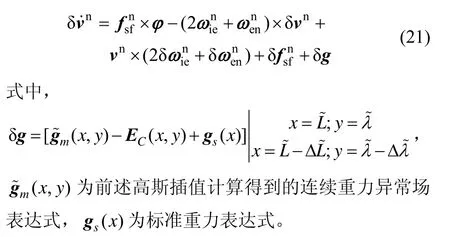
2.2 状态方程

除速度误差方程外导航系统其他误差方程利用传统思路方法参考相关文献建立[13]，于是可以定义SINS的状态变量如下，共15维状态矢量：

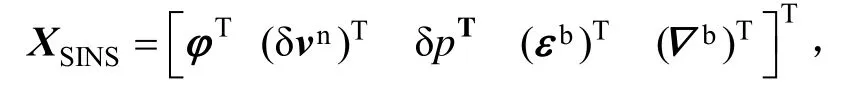
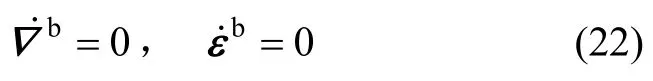
于是得到局部连续重力辅助导航精准模型方程:

式中，矩阵wSINS为6维系统干扰白噪声，矩阵GSINS是15×6噪声分配矩阵，矩阵FSINS是15×15状态矩阵。

2.3 量测方程

本文系统量测值取为重力仪量测重力与惯导指示位置对应重力图上重力之差作为观测方程。设定此时系统的量测方程Zg可由式(24)右边计算得出：

由于绘制成的重力图值，实质上等于实际重力测量值经过厄特弗斯修正而后减去标准重力值。所以对于实际位置点(L，)λ有：

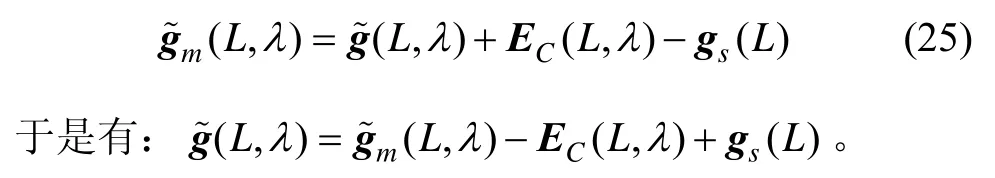
代入方程(24)经线性化处理后，可表示为方程(26)所示系统的量测方程为：

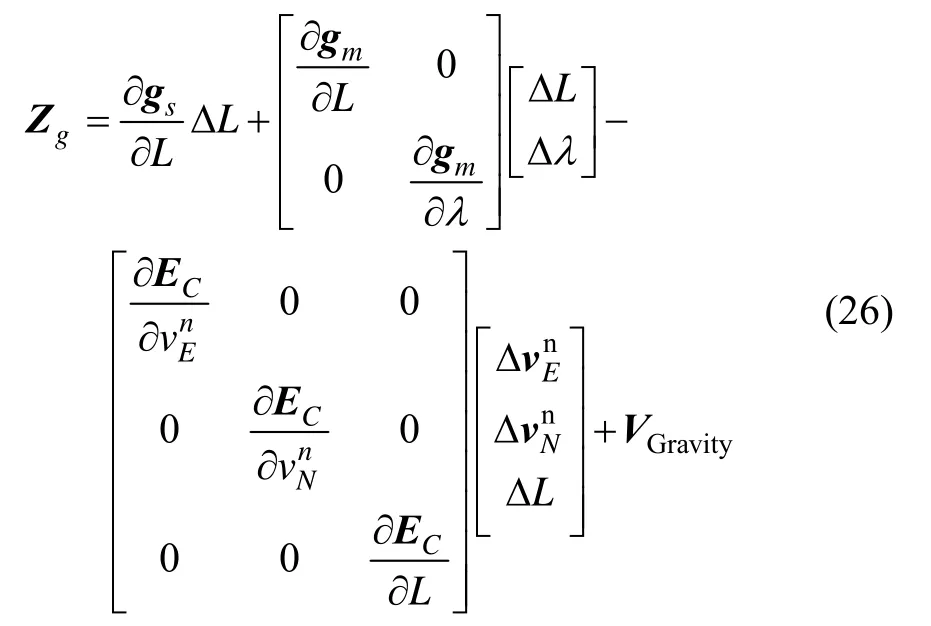
VGravity为重力传感器、重力异常图制作噪声和线性化误差总和，在实际计算中，重力异常梯度，可以采用九点拟合、全平面拟合等方法计算。

所以，根据式(32)确定其测量矩阵为

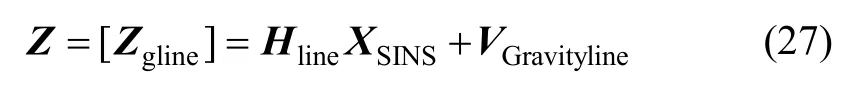
式中，Zgline为式(24)中计算得到的重力测量误差值，为1×15维观测矩阵。为重力传感器的噪声、重力异常图制作噪声和线形化误差总和。

3 仿真试验与分析

本文采用第二炮兵工程大学惯性导航实验室基于Matlab软件自行开发研制的惯性导航轨迹生成软件生成仿真需要的真实航迹和惯导指示航迹。重力异常数据使用渤海地区经度范围 118°～119°，纬度范围 37°～38°的真实数据，该重力异常场的三维图如图2所示。重力图分辨率为 1′×1′，重力仪的实时量测数据是利用真实航迹在重力数据库中的采样值叠加0.4 mGal的随机量测噪声获取，陀螺常值漂移取 0.01°/h，随机噪声漂移为0.01/h，加速度计随机常值零偏1×10-4g，随机噪声漂移为 1×10-5g；初始状态：速度 10 m/s、经度118.02°、纬度37.24°、惯导测量经维度误差0.02°、对准水平姿态误差角2′、对准航向误差角10′。运载体保持俯仰、横滚角 10°、航向角 30°的姿态，0.005 m/s2加速度每隔10 min加速一次，3 min采样匹配滤波一次，行进了70 min时间，得到24个测量点[12]。捷联惯导的情况下进行的仿真，对比分析了ICCP算法初次估计解算，局部连续场情况下传统重力辅助导航模型和本文叙述的基于高斯插值的精准重力辅助导航模型导航解算法导航效果（分别称其为tradition-ICCP和gausscompensation-ICCP算法，简记为TRAI和GACOI算法）。

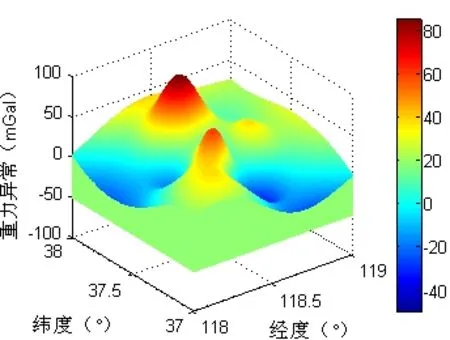
图2 重力异常场三维图Fig.2 3D map of gravity anomaly field

图3(a)～图3(b)为TRAI和本文GACOI新算法（最优局部支撑参数）导航的经、纬度位置误差，航向、俯仰、横滚姿态误差角，东、北、天向速度误差分布图。如图3中所示：TRAI算法导航位置误差在 125～330 m、平均 210 m，水平姿态误差在0.2′～0.75′、平均 0.50′，航向姿态误差在 4′～9′、平均误差7.5′，速度误差在0.027～0.085 m/s、平均误差0.045 m/s；本文 GACOI新算法导航能够保持在100～200 m、平均110 m的位置误差，0.01′～0.25′、平均 0.18′的水平姿态误差，2′～6′、平均 2.5′的航向姿态误差，0.002～0.05 m/s、平均0.016 m/s的速度误差。可见，本文 GACOI导航新算法将传统重力辅助惯性导航算法的位置导航精度提高了1倍左右，姿态角导航精度、速度导航精度提高了1～2倍。可见新算法引入了先进的局部支撑模型参数确定方法，同时建了考虑重力扰动矢量、标准重力值误差、厄特弗斯修正计算值的精准重力辅助导航模型进行导航解算提高了导航精度，达到了接近于高精度导航的水平。

图3 导航仿真误差分析图Fig.3 The analysis of navigation simulation errors

4 结 论

本文从分析重力辅助导航所需的地球重力场数学建模开始，通过对高斯样条优化插值所涉及到的系数矩阵可逆性进行研究，得出了局部支撑参数的最大限度值，紧接着通过分析与之相关的求逆误差进一步印证了结论的准确性，给出了局部支撑参数的数值区间，接着对插值模型精度评估理论进行研究，设计了给定区间上的最优局部支撑参数求解方法，而后建了考虑重力扰动矢量、标准重力值误差、厄特弗斯修正计算值的精准重力辅助导航模型。最终实现了重力辅助导航算法的精确导航定位计算。本文研究内容不但可以为重力辅助惯性导航算法的实践化做一定的理论铺垫，而且相关理论研究对推进数学高斯插值相关研究也有一定的意义，当惯性导航系统导航观测模型为非线性情况下，如何在高斯样条逼近模型的基础上展开相应的滤波算法有待进一步研究。

References)

[1]Mcphail S.Autosub6000:A deep diving long range AUV[J].Journal of Bionic Engineering，2009(6):55-62.

[2]李姗姗，吴晓平，马彪.水下重力异常相关极值匹配算法[J].测绘学报，2011，40(4)：464-470.LI Shan-shan，WU Xiao-ping，MA Biao.Correlative extremum matching algorithm using underwater gravity anomalies[J].Acta Geodaetica et Cartographica Sinica，2011，40(4):464-470.

[3]袁赣南，张红伟，袁克非，吴简彤.基于重力梯度辅助定位的概率神经网络改进方法[J].中国惯性技术学报，2013，21(3)：369-374.YUAN Gan-nan，ZHANG Hong-wei，YUAN Ke-fei，WU Jian-tong.Improved probabilistic neural network method based on gravity gradient aided location[J].Journal of Chinese Inertial Technology，2013，21(3):369-374.

[4]Jiang F，Wu Y M，Zhang Z S，et al.Combinational seabed terrain matching algorithm basing on probability data associate filtering and iterative closest contour point[C]//2009 Second International Conference on Intelligent Computation Technology and Automation.IEEE Computer Society，Piscataway，2009:245-249.

[5]Yuan G N，Zhang H W，Yuan K F.A Combinational underwater aided navigation algorithm based on TERCOM/ICCP and Kalman filter[J].IEEE Journal of Sciences and Optimization，2011，23(1):952-955.

[6]Wang Z G，Bian S F，Xiao S H.A local geopotential model for implementation of underwater passive navigation[J].Progress in Natural Science，2008，18(9):1139-1145.

[7]童余德，边少锋，将东方.一种新的基于局部重力图逼近的组合匹配算法[J].地球物理学报，2012，55(9)：2917-2925.TONG Yu-de，BIAN Shao-feng，JIANG Dong-fang.A new integrated gravity matching algorithm based on approximated local gravity map[J].Chinese Journal of Geophysics，2012，55(9):2917-2925.

[8]Dransfield M，ZENG Y.Airbone Gravity gradiometry:Terrian corrections and elevation error[J].Geophysics，2009，74(5):137-142.

[9]李胜全，欧阳永忠，常国宾.惯性导航系统重力扰动量补偿技术[J].中国惯性技术学报，2012，20(4)：410-414.LI Sheng-quan，OUYANG Yong-zhong，CHANG Guo-bin.Compensation technology of gravity disturbance vector in inertial navigation system[J].Journal of Chinese Inertial Technology，2012，20(4):410-414.

[10]DeGregoria A.Gravity gradiometry and map matching an aid to aircraft inertial navigation systems[D].Ohio:Air Force Institute of Technology，2010.

[11]Senobari M.New results in airborne vector gravimetry using strapdown INS/DGPS[J].Journal of Geodesy，2010，84:277-291.

[12]Neumeyer J，Schäferb U，Kremerc J，et al.Derivation of gravity anomalies from airborne gravimeter and IMU recordings-Validation with regional analytic models using ground and satellite gravity data[J].Journal of Geodynamics，2009，47:191-200.

Constructive model algorithm for gravity aided navigation in local anomaly field

WEN Chao-bin1，2，WANG Yue-gang1，TIAN Qi1，GUO Zhi-bin1，ZUO Zhao-yang1，YANG Jia-sheng1
(1.304 Unit，The Second Artillery Engineering University，Xi’an 710025，China;2.Unit 96124 of the Chinese people’s liberation army，Tonghua 134000，China)

In studying high-precision gravity aided navigation，it is indispensable to build a local continuous gravity anomaly field model with high precision and good analytic property，and accurately compensate the gravity in error equation.To solve the choice problem of local support optimal parameters in local continuous gravity anomaly field model with 2D gauss spline interpolation，an local support optimal calculation method is proposed by studying the related problems such as，coefficient of matrix，solution errors，and interpolation model evaluation，etc.Then a high-precision construct algorithm based on the gravity aided navigation model is put forward，which has compensated the gravity disturbance vector，standard gravity value error and eotvos effect.The experiment results show that the positioning accuracy is increased by about 1 times，the attitude and the velocity are both increased by 1～2 times.Its latitude and longitude errors are kept within 100～300 m.

gravity aided navigation;gauss spline interpolation;gravity error compensation;navigation model

U666.1

A

1005-6734(2014)03-0368-06

10.13695/j.cnki.12-1222/o3.2014.03.017

2013-12-25；

2014-04-11

国防预研（103030203）

文超斌（1986—），男，博士研究生，从事导航、制导与控制研究。E-mail：weijing123@126.com

联 系 人：王跃钢（1958—），男，教授，博士生导师。E-mail：wangyueg@163.com