基于比例多重积分观测器的三轴惯性稳定平台加速度计测角误差估计

钟麦英，矫成斌，李树胜，赵 岩

（北京航空航天大学 惯性技术与导航仪器系，北京 100191）

基于比例多重积分观测器的三轴惯性稳定平台加速度计测角误差估计

钟麦英，矫成斌，李树胜，赵 岩

（北京航空航天大学 惯性技术与导航仪器系，北京 100191）

航空遥感三轴惯性稳定平台用于有效隔离飞行载体的偏航及姿态角运动，使成像载荷沿航向平稳飞行并保持载荷视轴对地垂直指向。通常情况下，稳定平台采用高精度位置姿态测量系统(Position and Orientation System，POS)作为姿态角传感器，一旦POS发生故障会导致平台失稳甚至危及载荷安全。为了提高平台运行可靠性并保证载荷安全，考虑了一种以加速度计作为姿态角冗余传感器的双工作模式，即POS组合工作模式和自主工作模式。当POS发生故障时平台切换到自主工作模式，依靠平台自身加速度计组件进行姿态控制。但与POS相比，加速度计测角易受载体扰动加速度影响从而导致测角误差较大，严重影响平台的稳定精度。针对这一问题，提出了一种基于比例多重积分（Proportional and Multiple-integral，PMI）观测器的加速度计测角误差估计方法，对平台系统建模及PMI观测器的设计过程进行了详细的论述，并利用真实飞行实验数据进行了性能测试。结果表明该方法对实际误差的估计精度达到0.0701°（RMS），可较好的估计出加速度计测角误差，为提高平台自主工作模式的稳定精度奠定基础。

三轴惯性稳定平台；加速度计；自主工作模式；比例多重积分观测器

高分辨率对地观测系统的高精度实时运动成像要求飞行载体做匀速直线运动，但在实际飞行过程中，由于受到阵风、湍流等外部扰动以及发动机振动等内部扰动的影响，飞行载体的非理想运动不可避免地使成像载荷视轴不稳定，从而导致成像质量下降[1-2]。三轴惯性稳定平台用于有效隔离飞行载体的偏航及姿态角运动，使成像载荷沿航向平稳飞行并保持载荷视轴对地垂直指向，以满足高精度实时运动成像要求[3-4]。

通常情况下，由安装在成像载荷上的位置姿态测量系统(Position and Orientation System，POS)作为平台姿态角测量传感器，为平台三框架闭环控制提供姿态信息[3]。一旦POS发生故障会导致平台失稳甚至危及载荷安全，为了提高平台运行可靠性及保证载荷安全，本文考虑了一种以加速度计作为姿态角冗余传感器的双工作模式，即POS组合工作模式和自主工作模式。当POS发生故障时切换到自主工作模式，依靠平台自身加速度计组件进行姿态控制[5]。但与POS组合工作模式相比，自主工作模式下的加速度计测角易受飞行载体运动加速度影响从而导致测角误差较大[6]，若直接进行反馈易使平台稳定精度下降。因此有必要采取措施对自主工作模式下的加速度计测角误差进行估计，进而进行有效补偿，以提高三轴惯性稳定平台自主工作模式下的稳定精度。

目前针对加速度计随机误差和测量噪声进行处理的研究较多[7-9]，而对于稳定平台加速度计测角误差的研究则十分有限。文献[6]利用互补卡尔曼滤波器充分融合平台速率陀螺和加速度计信息，一定程度上减小了加速度计测角误差，但该文献并没有针对扰动加速度进行建模，因此并不能从本质上解决加速度计测角误差问题。文献[10]提出一种比例多重积分(Proportional and Multiple-integral，PMI)观测器设计方法，并将其应用于实际车辆横向系统的故障估计。PMI观测器能够在未知输入扰动作用下同时估计出系统状态和传感器误差[10-12]，有助于解决平台自主工作模式下加速度计测角误差估计问题。本文首先对存在加速度计测角误差的系统进行建模，在此基础上提出了一种基于PMI观测器的加速度计测角误差估计方法，实时估计出加速度计测角误差，为三轴惯性稳定平台自主工作模式提供较为精确的位置反馈信息，为提高平台自主工作模式的控制精度奠定基础。

1 系统建模与问题描述

1.1 系统建模

三轴惯性稳定平台的结构如图1所示，由三个框架构成，由外至内分别是横滚框、俯仰框和方位框。位置姿态系统(Position and Orientation System，POS)安装在对地观测载荷上，用于测量载荷相位中心相对于当地导航坐标系的姿态角，同时可作为平台姿态角测量传感器；Mx、My、Mz为三台力矩电机，分别用来驱动横滚框、俯仰框和方位框的转动；Gx、Gy、Gz为安装在框架上的速率陀螺，其中Gx敏感横滚框相对于惯性空间的转动角速度，Gy敏感俯仰框相对于惯性空间的转动角速度，Gz敏感方位框相对于惯性空间的转动角速度；Ax、Ay为安装在俯仰框上的加速度计，其中Ax的敏感轴与横滚框的旋转轴重合，Ay的敏感轴与俯仰框的旋转轴重合，用于测量平台框架的水平倾角。

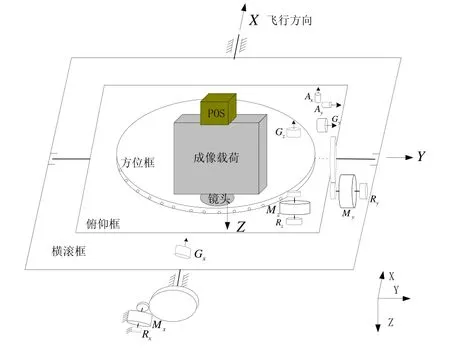
图1 航空遥感三轴惯性稳定平台结构示意图Fig.1 Layout of three-axis ISP for airborne remote sensing

以平台俯仰框为例，其工作原理如图2所示，正常航拍过程中平台处于POS组合工作模式，此时POS作为姿态角测量传感器，控制器根据给定姿态和POS测量出的姿态信息产生控制信号驱动框架转动以达到稳定和跟踪当地地理水平的目的。但当POS发生故障时，平台切换到自主工作模式，此时由加速度计输出的比力信息解算得到框架姿态角，并用于平台位置闭环。本文主要研究平台自主工作模式下的加速度计测角误差估计问题。

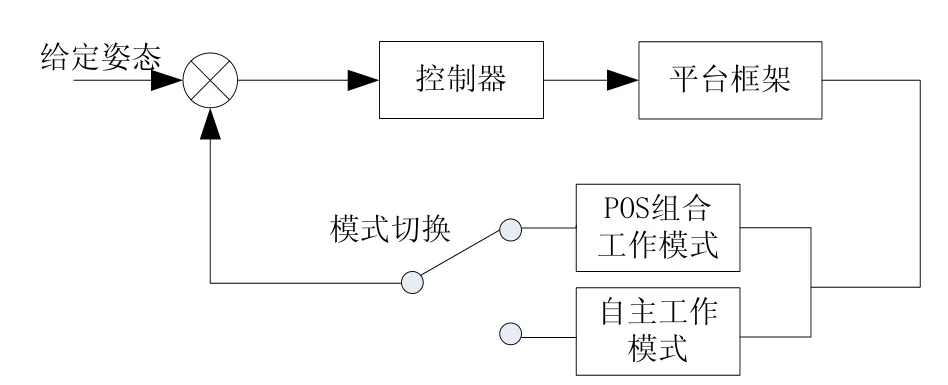
图2 平台工作原理图Fig.2 Scheme of the platform working principle

航空遥感用高精度三轴惯性稳定平台需要承载质量较大的成像载荷，结构上采用电机和一级齿轮减速相结合的间接驱动方式[5]。建立该部分的传递函数模型，需要进行电机端和平台端的 力矩、角速度及转动惯量的相关转换，转换公式如下：

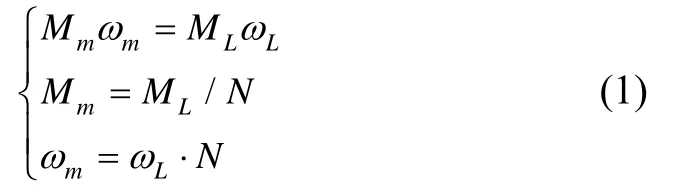
其中，Mm和ωm分别为电机输出转矩和旋转角速度，ML和ωL分别为平台转矩和角速度，N为传动比，JmL为转换到平台端的电机转子转动惯量。

由直流力矩电机原理、力矩方程以及公式(1)、(2)我们可以得到平台的系统模型为[5]：

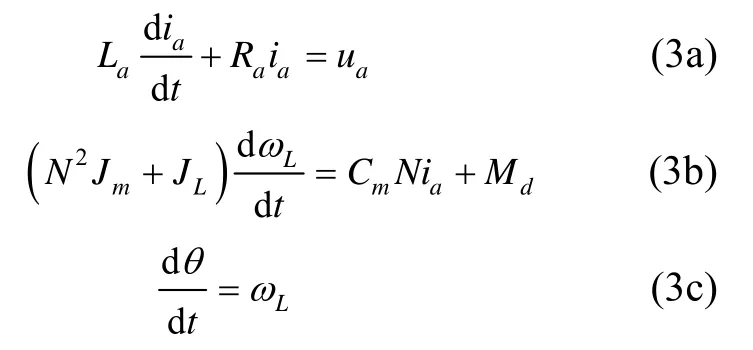
其中，La为电机电枢电感，Ra为电枢绕组，ia为电机电枢电流，Ce为电机反电动式系数，ωL为框架角速度，ua为电机控制电压，Jm为电机转子转动惯量，JL为负载转动惯量，Cm为电机的力矩系数，Md为系统总的干扰力矩，θ为框架角。

1.2 问题描述

由加速度计的工作原理知：加速度计测量的是比力信息，当物体静止或匀速运动时，根据其上加速度计输出信号与重力矢量之间的关系可计算出水平姿态角，其测角原理如图3所示。

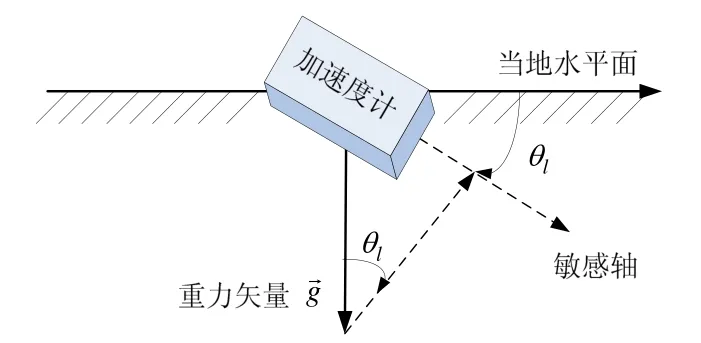
图3 加速度计测角原理Fig.3 Angle measure by accelerometer

由此可以计算出框架与当地水平面之间夹角，即水平姿态角θl的大小：

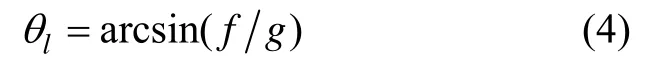
其中，θl为水平姿态角，f为加速度计输出的比力，g为当地的重力加速度。由于平台框架运动范围较小(小于5°)，因此可以对公式(4)进行小角度线性化，即：

但是飞行载体在实际飞行过程中不可避免的会存在时变扰动加速度，导致加速度计测角误差较大。由于时变扰动加速度的垂直分量较小，本文主要考虑时变扰动加速度的水平分量（以水平加速度分量a→为例），此时加速度计测得的比力信息为如下形式：

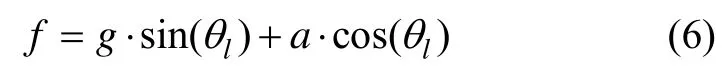
此时，按照公式(5)进行计算可得加速度计测得的水平倾角为：

由公式(7)可知由于未知水平加速度分量a→的存在，加速度计测得的水平倾角存在较大的误差，不能准确反映出平台真实的姿态信息，如果直接将解算出来的lθ′进行闭环反馈则平台处于自主工作模式时会出现无规则的晃动，影响平台自主工作模式的稳定精度，因此必须采取有效措施获取相对准确的平台框架姿态角。本文首先建立存在加速度计测角误差的系统模型；然后设计PMI观测器实时估计出加速度计测角误差，为三轴惯性稳定平台自主工作模式提供较为精确的姿态反馈信息。

2 基于PMI观测器的加速度计测角误差估计

2.1 存在加速度计测角误差的系统模型

质量不平衡力矩主要包括静基座不平衡力矩和动基座不平衡力矩两大类。动基座不平衡力矩指在航摄时，由重力加速度和作用在三轴惯性稳定平台上的扰动加速度共同产生的扰动力矩。

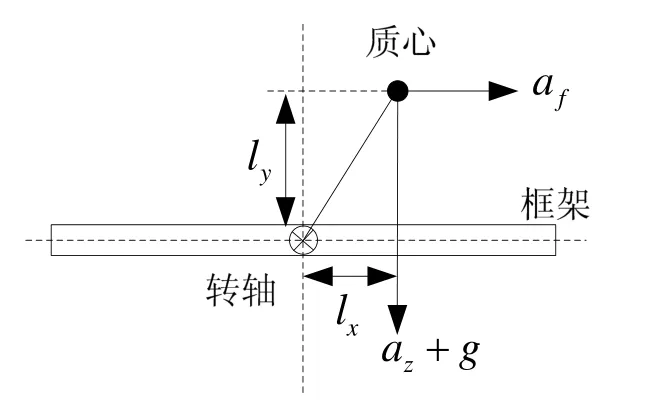
图4 动基座不平衡力矩示意图Fig.4 Sketch map of dynamic imbalance torque

三轴惯性稳定平台动态质量不平衡力矩作用示意图如图4所示，其数学表达式为[13]：

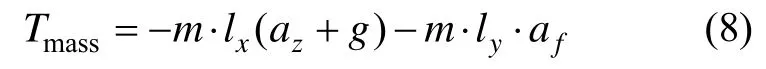
其中，Tmass为三轴惯性稳定平台的动态不平衡力矩，m为框架与载荷的总质量，lx和ly分别代表相对于框架水平方向和垂直方向的不平衡力臂，az为垂直方向上的扰动加速度分量，af为水平方向上的扰动加速度分量。

由公式(8)可知动态不平衡力矩主要有两部分组成，本文将垂直方向上的加速度分量引起的不平衡力矩可作为总的干扰力矩的一部分；而将水平方向上的加速度分量引起的干扰力矩视为加速度计测角误差引起的干扰力矩。因此公式(3b)应改写为：

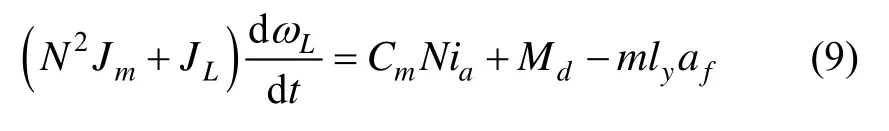
此时自主工作模式的三环控制结构图如图5所示。

选取三轴惯性稳定平台的框架角速度ωL和框架角θ为状态变量，框架角速度ωL和框架角θ为输出变量，视水平方向的扰动加速度af与重力加速度g的比值为加速度计测角误差fs，根据稳定平台的系统模型

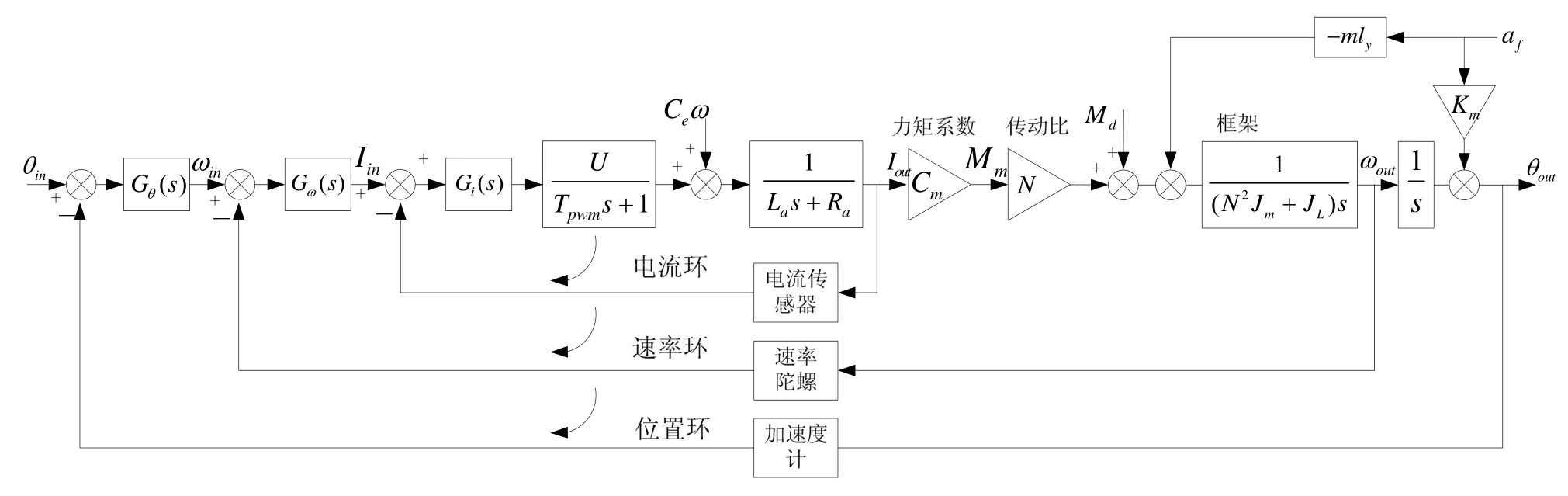
图5 控制系统结构图Fig.5 Configuration of the control system

建立如下状态空间描述：

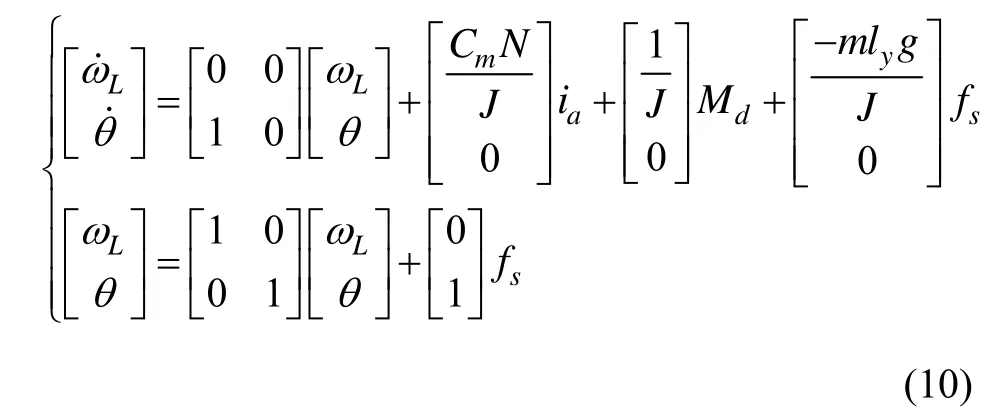
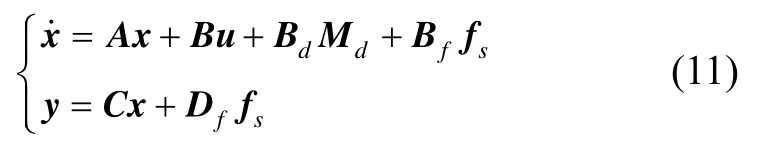
其中，系数矩阵定义如下：

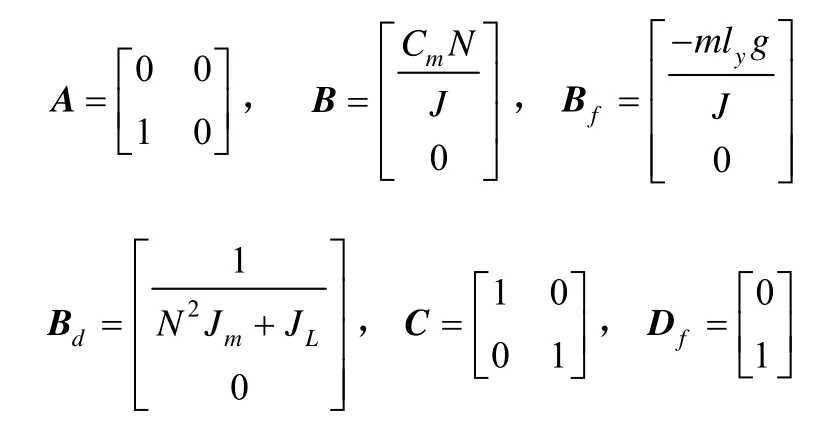
2.2 PMI观测器设计

不失一般性，可将三轴惯性稳定平台加速度计测角误差fs近似描述成由如下多项式函数形式[14]：

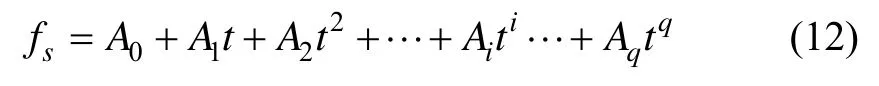
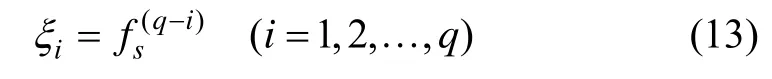
系统的参数矩阵满足如下条件：

因此针对形如(14)的状态空间表达式存在如下状态观测器：

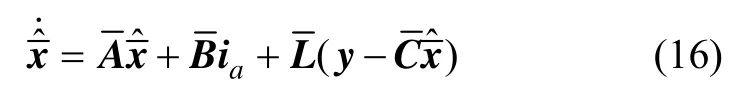
选取一个μ值满足如下不等式：

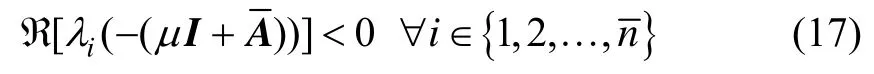
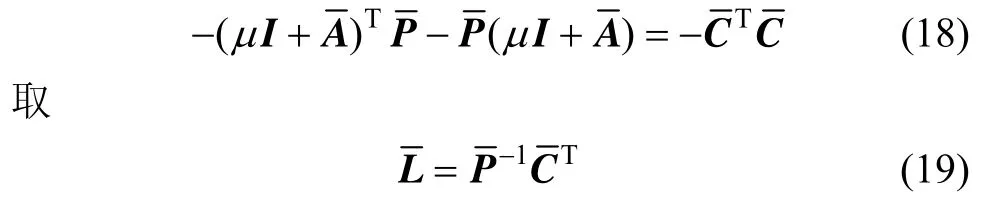
于是公式(18)等价于：

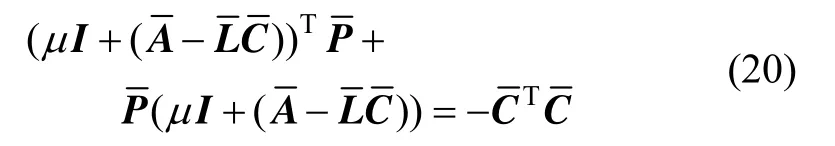
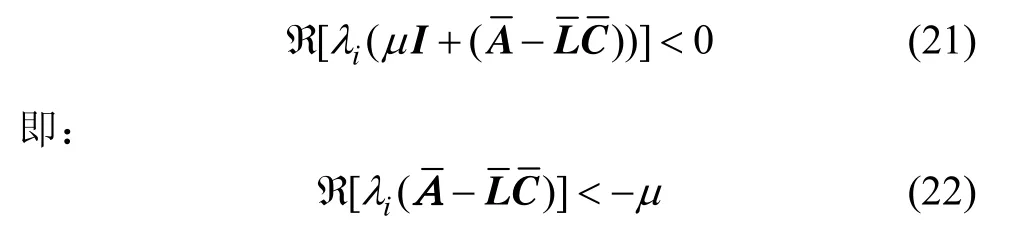
综上，通过选择合适的μ值，由公式(18)、(19)即可求得观测器增益矩阵，将观测器的极点配置在小于-μ的区域。同时，文献[10]给出稳态时的状态估计误差的上界值：

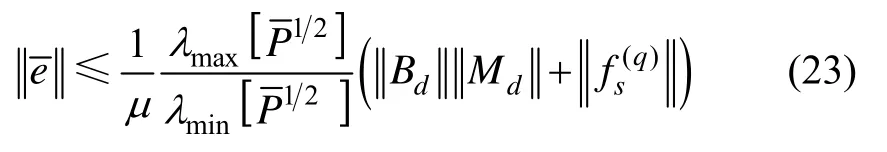
3 实验验证

3.1 参数计算

通过实验室内静基座基础上的实验结果，确定系统模型中的ly，静基座上的干扰力矩主要是质量不平衡力矩，其表达式如下：

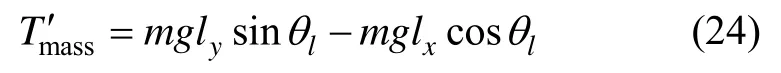
其中，lθ为框架角，为静基座下的质量不平衡力矩总和。

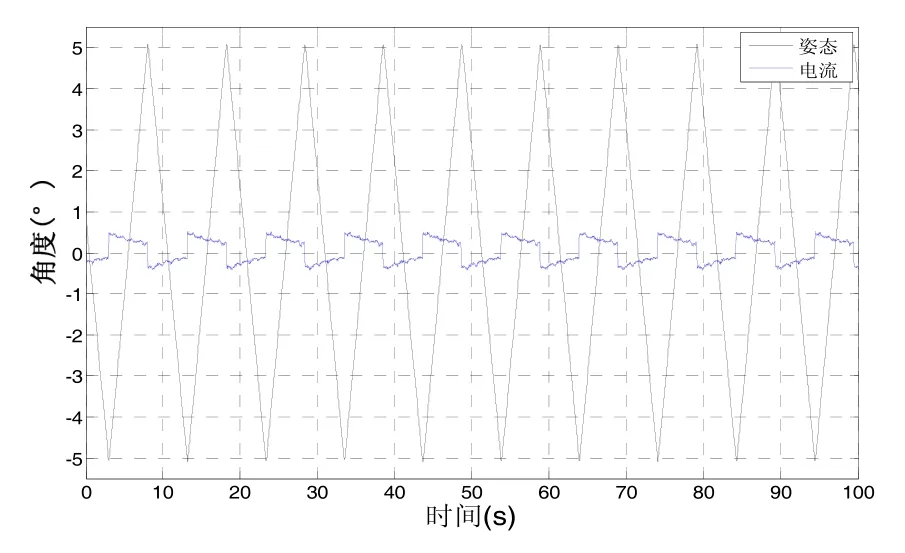
图6 俯仰框姿态与电机电枢电流对比图Fig.6 Pitch frame posture and motor current comparison chart

静基座下，令平台俯仰框以±2 (°)/s的角速率在±5°范围内进行摇摆伺服运动，得到电流和姿态对比如图6所示。此时电机输出力矩，完全用于克服干扰力矩（主要是不平衡力矩和摩擦力矩，其中摩擦力矩值可视为常数C）。可以得到如下表达式：

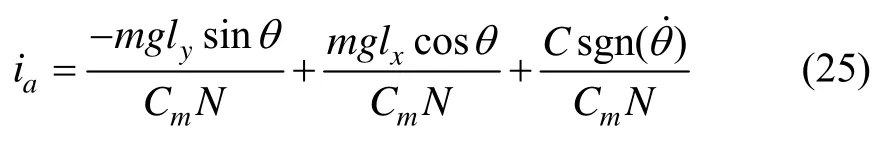
系统参数理论值如表1所示，结合公式(25)和图5通过数据拟合求得参数ly≈0.0232 m，在这里选取q=2和μ=8进行PMI观测器设计，求得观测器增益矩阵为：

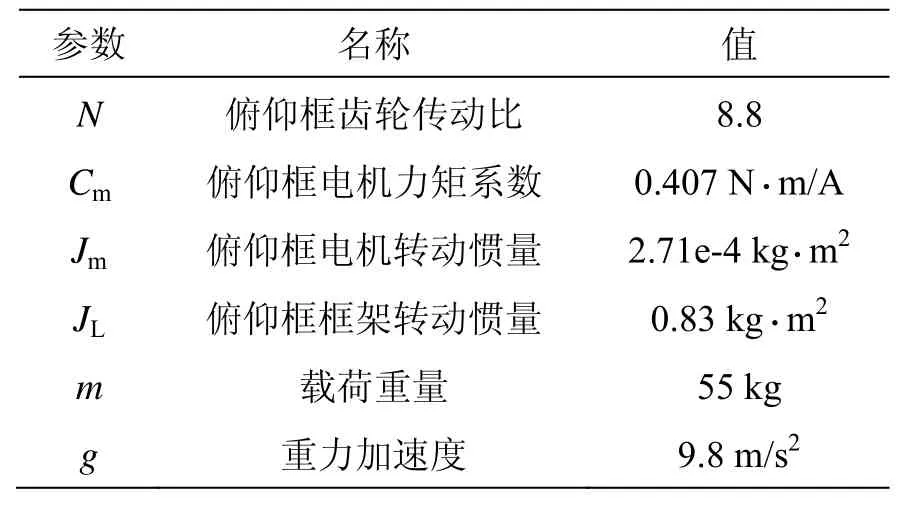
表1 系统参数理论值Tab.1 System parameters of the theoretical value

3.2 实验验证

现以作者所在实验室研制的高精度大负载三轴惯性稳定平台为实验对象，采用真实飞行实验数据来验证所设计的PMI观测器的有效性。实验设备如图7、图8所示，包括飞行载体、三轴惯性稳定平台、成像载荷、高精度 POS、PC上位机、电源等，实验过程中三轴惯性稳定平台工作在 POS组合工作模式，由PC上位机采集平台各传感器信息，离线代入到所设计的PMI观测器中进行计算验证。

实验中采用的高精度 POS的水平姿态实时精度为0.005°(1σ)，此处将POS输出的姿态信息视为真值。实验数据处理结果如图9所示，其中真实误差表示了加速度计输出信息和POS输出信息的差值。

图7 飞行载体Fig.7 Flight vehicle

图8 实验设备Fig.8 Experiment equipment

计算结果显示：采用本文所设计的方法，对实际误差的估计精度达到0.0701°（RMS）。表明：当存在外界时变加速度扰动时，所设计的PMI观测器能够较好的估计出水平加速度计测角误差，为平台自主工作模式下干扰量的估计提供了一种有效的方法。

由于状态空间表达式中所用数据均为平台设计过程的理论值，与实验采用的真实平台存在差异。同时，本文只对时变加速度水平扰动分量对加速度计测角误差的影响进行了讨论，因垂直扰动分量较小，故予以忽略。这都是影响估计效果存在误差的原因。这部分内容将在后续研究中深入进行。

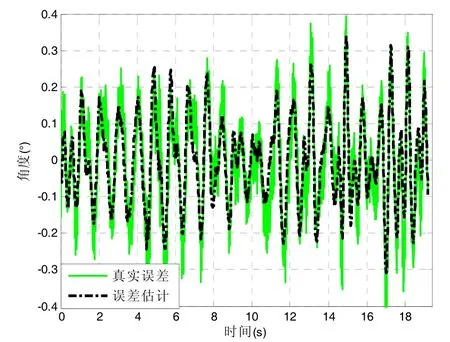
图9 实验数据处理结果Fig.9 Results of experiment data processing

4 结 论

针对三轴惯性稳定平台自主工作模式下加速度计测角受载体扰动加速度影响较大这一问题，在介绍了常规系统建模、加速度计测角原理、动态不平衡力矩作用机理的基础上，建立了存在加速度计测角误差的系统模型，进而设计了PMI观测器用于实时估计加速度计的测角误差。并利用真实飞行实验数据进行了性能测试，结果表明所设计的PMI观测器能够较好的估计出加速度计测角误差，对实际误差的估计精度达到0.0701°（RMS），验证了方法的有效性，为进一步对平台进行高精度的控制奠定基础。

（References）：

[1]周向阳，赵强.航空遥感三轴惯性稳定平台双速度环控制[J].中国惯性技术学报，2013，21(4)：439-445.ZHOU Xiang-yang，ZHAO Qiang.Dual rate-loop control method of three-axis inertially stabilized platform for aerial remote sensing application[J].Journal of Chinese Inertial Technology，2013，21(4):439-445.

[2]Jiang F，Ding H S，Fu T.Orientation density and workspace analysis of a parallel stabilized platform testing system[J].Journal of Beijing Institute of Technology，2012，21(3):302-308.

[3]房建成，戚自辉，钟麦英.航空遥感惯性稳定平台不平衡力矩前馈补偿方法[J].中国惯性技术学报，2010，18(1)：38-43.FANG Jian-cheng，QI Zi-hui，ZHONG Mai-ying.Feedforward compensation method for three axes inertially stabilized platform imbalance torque[J].Journal of Chinese Inertial Technology，2010，18(1):38-43.

[4]Li S S，Zhong M Y.The internal model control design of three-axis inertially stabilized platform for airborne remote sensing[C]//IEEE Instrumentation and Control Technology.London，2012 :5-10.

[5]Mu Q Q，Liu G.，Zhong M Y.Imbalance torque compensation for three-axis inertially stabilized platform using acceleration feedforward[C].IEEE Instrumentation and Control Technology.London，2012:157-160.

[6]杜超超.三轴惯性稳定平台稳定精度分析与控制[D].北京：北京航空航天大学硕士学位论文，2012.DU Chao-chao.Three-axis inertial stabilized platform stabilization precision analysis and control[D].Beijing University of Aeronautics and Astronautics:A dissertation submitted for the degree of master，2012.

[7]Kazuaki I，Riccardo A，Roberto O.Use of MEMS accelerometers for performance improvement of motion control systems with low resolution position sensors[C]//ISIE.Taiwan，May，2013:1-6.

[8]殷广冬，王建立，孟浩然，等.基于加速度计的望远镜平台抖动测量与分析[J].传感器与微系统，2013，32(11)：125-131.YIN Guang-dong，WANG Jian-li，MENG Hao-ran，et.al.Telescope platform jitter measurement and analysis based on accelerometer[J].Transducer and Microsystem Technologies，2013，32(11):125-131.

[9]Yuta Teruyama，Takashi Watanabe.A basic study on variable-gain Kalman filter based on angle error calculated from acceleration signals for lower limb angle measurement with inertial sensors[C]//35thAnnual International Conference of the IEEE EMBS.Osaca，Japan，July，2013:3423-3426.

[10]Z Gao，Steven X D，Y Ma.Robust fault estimation approach and its application in vehicle lateral dynamic systems[J].Optimal Control Applications and Methods，2007:143-156.

[11]Wu A G，Feng G，Duan G R.Proportional multiple-integral observer design for discrete-time descriptor linear systems J].International Journal of Systems Science，2012，43(8):1492-1503.

[12]Tang Y M，Patton R J.Active FTC for non-linear aircraft based on feedback linearization and robust estimation[C]//The 8th IFAC Symposium on Fault Detection，Supervision and Safety of Technical Processes.August 29-31，2012，Mexico City，Mexico.

[13]白长瑞.三轴惯性稳定平台扰动抑制与补偿技术研究[D].北京：北京航空航天大学硕士学位论文，2012.BAI Chang-rui.Research on the disturbance rejection and compensation technology for triaxial inertial stabilized platform[D].Beijing University of Aeronautics and Astronautics:A dissertation submitted for the degree of master，2012.

[14]Youssef Y，Chadli M，Karimi H R.Chaos synchronization based on unknown input proportional multipleintegral fuzzy observer[J].Abstract and Applied Analysis，2013，151(3):279-288.

Error estimation of angle measured by accelerometer based on PMI observer for three-axis inertially stabilized platform

ZHONG Mai-ying，JIAO Cheng-bin，LI Shu-sheng，ZHAO Yan
(Department of Inertia Technology and Navigation Guidance Instrument，Beihang University，Beijing 100191，China)

Three-axis inertially stabilized platform for airborne remote sensing is used to isolate the impact of flight vehicle attitude angular motion to improve the image quality and operational efficiency.Normally，the stabilized platform uses a POS as attitude angle sensor.Once the POS has failure，it will lead to instability and even endanger the load platform security.In order to improve the operational reliability of the platform and the safety of the load，a kind of dual modes is proposed，that is，the POS combination mode and the independent mode.The platform switch to independent mode when the POS has failure，and the platform uses the accelerometer for attitude control.But compared with POS，an accelerometer has a larger angle measuring error which affects the stability precision of the platform seriously.In order to solve this problem，this paper proposes a method of accelerometer measuring error estimation based on PMI observer.Then a system modeling and the design process of the PMI observer is discussed.The performance tests are carried out by using real flight experiment data.The experimental results show that this method can effectively estimate the accelerometer angle measuring error to the accuracy of 0.0701°(RMS)，which provides the basis for improving the accuracy of the platform.

three-axis inertially stabilized platform;accelerometer;independent work mode;PMI observer

钟麦英（1965—），女，教授，博士生导师。E-mail：myzhong@buaa.edu.cn

U666.1

A

1005-6734(2014)03-0311-06

10.13695/j.cnki.12-1222/o3.2014.03.007

2014-01-09；

2014-04-21

国家自然科学基金（60825305，61104198）