Banach空间中线性离散时间系统的一致多项式膨胀性

雷国梁,岳田,宋晓秋

(1.湖北汽车工业学院理学院,湖北十堰442002;2.中国矿业大学理学院,江苏徐州221008)

Banach空间中线性离散时间系统的一致多项式膨胀性

雷国梁1,岳田1,宋晓秋2

(1.湖北汽车工业学院理学院,湖北十堰442002;2.中国矿业大学理学院,江苏徐州221008)

给出了Banach空间中线性离散时间系统一致多项式膨胀性的概念,并讨论了其离散特征.借助Lyapunov函数给出了线性离散时间系统满足一致多项式膨胀的充要条件.所得结论将一致指数稳定性、指数膨胀性及多项式稳定性中的若干经典结论推广到了一致多项式膨胀性的情形.

线性离散时间系统;一致多项式膨胀性;Lyapunov函数

1 引言

近年来,关于有限或无限维Banach空间中演化方程解的渐近行为研究取得了突破性的进展,尤其对于演化型算子的指数型渐近行为做了大量研究,获得了非常丰富的成果[113].如文献[1]利用Banach函数空间及序列空间给出了Banach空间中斜积半流一致指数不稳定的充要条件;文献[2-3]分别讨论了Banach空间中演化族与斜积流的一致指数不稳定性;文献[4]利用完全容许性给出了线性斜积流一致指数膨胀的离散和连续型特征;文献[7-8]分别对Banach空间中演化族及斜演化半流的弱指数膨胀性进行了相关讨论,给出了满足相应概念的若干充要条件.对于线性离散时间系统解的指数型渐近行为,文献[9-11]分别给出了其满足指数稳定、指数二分、指数三分的若干离散特征.

自从Barreira L,Valls C[14]提出多项式渐近概念以来,关于演化方程多项式的渐近行为的研究已成为一个热点问题,但目前大都局限于多项式稳定性方面的研究.如文献[15]针对演化算子提出了一致多项式稳定、Barreira-Valls意义下多项式稳定、非一致多项式稳定三个概念,并分别给出了相应的积分特征,同时指出了三者之间的联系与区别;文献[16]重点讨论了演化算子在Barreira-Valls意义下呈多项式稳定的相关特征.与多项式稳定性相比,演化方程多项式膨胀性研究相对较少,本文将在上述文献的基础上,给出Banach空间中线性离散时间系统一致多项式膨胀性概念,利用指数型渐近行为研究方法,给出其相应的充要条件.且作为应用,借助Lyapunov函数给出线性离散时间系统一致多项式膨胀性的特征.

2 预备知识

设X为一实或复的Banach空间,记空间X上的范数及作用其上的有界线性算子全体B(X)中的范数为||·||.记

I为X上的恒等算子.

考虑如下线性离散时间系统:

其中A:N→B(X)是B(X)中的一个序列.则系统(1)的每个解x={xn}将可表示为:

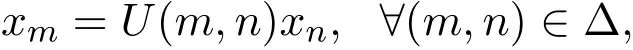
其中,定义映射:

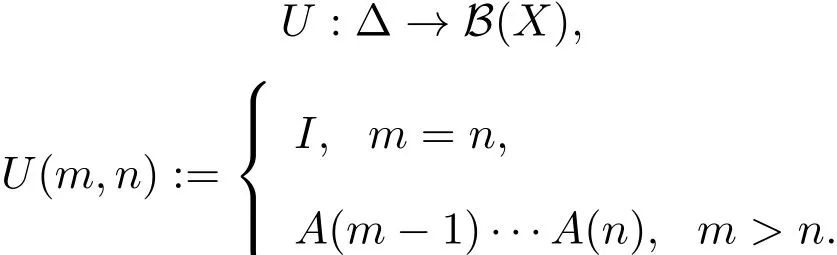
由此可以验证如下关系成立:

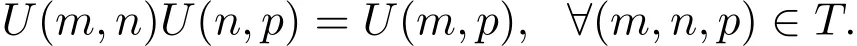
特别地,当(1)式为一个自治系统,即

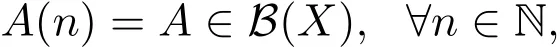
则有

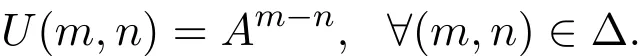
定义2.1称系统(1)为一致多项式膨胀的,如果存在两个常数N≥1及α>1,使得

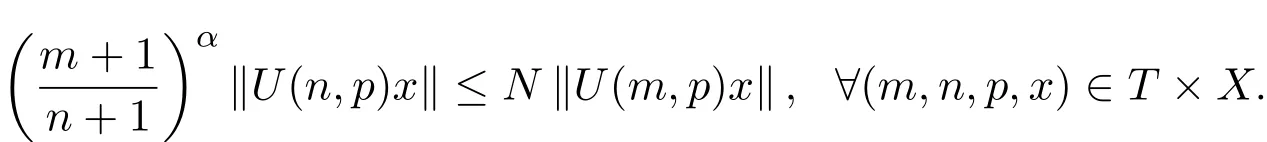
注2.1显然,系统(1)是一致多项式膨胀的当且仅当存在两个常数N≥1及α>1,使得

但现在，我发现我错了，却不知错在哪里。错在我当初的选择吗？错在我没有教学能力吗？错在我的教学水平越来越低吗？

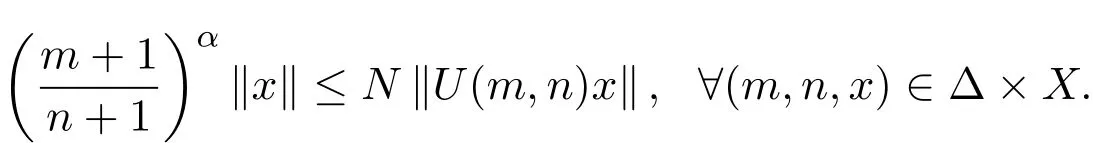
例2.1设X=R,考虑映射:

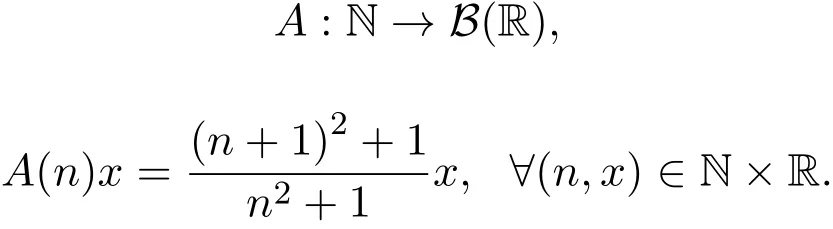
则

进而

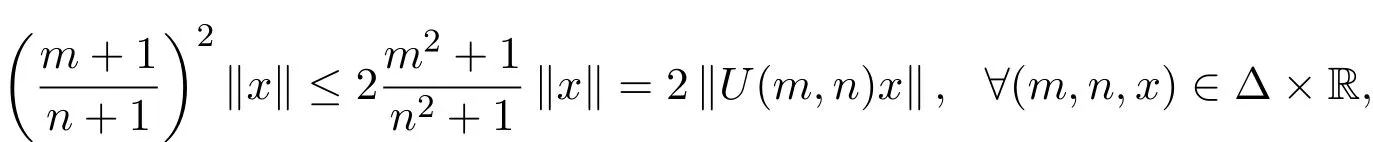
故在定义2.1中取N=α=2,即可得系统(1)是一致多项式膨胀的.

定义2.2称映射L:∆×X→R为系统(1)的一致多项式膨胀Lyapunov函数,如果存在常数µ>1,使得

3 主要结论

定理3.1系统(1)是一致多项式膨胀的当且仅当存在常数M≥1,ω>0,L≥1及l>0,使得∀(m,n,p,x)∈T×X,有如下两个不等式成立:

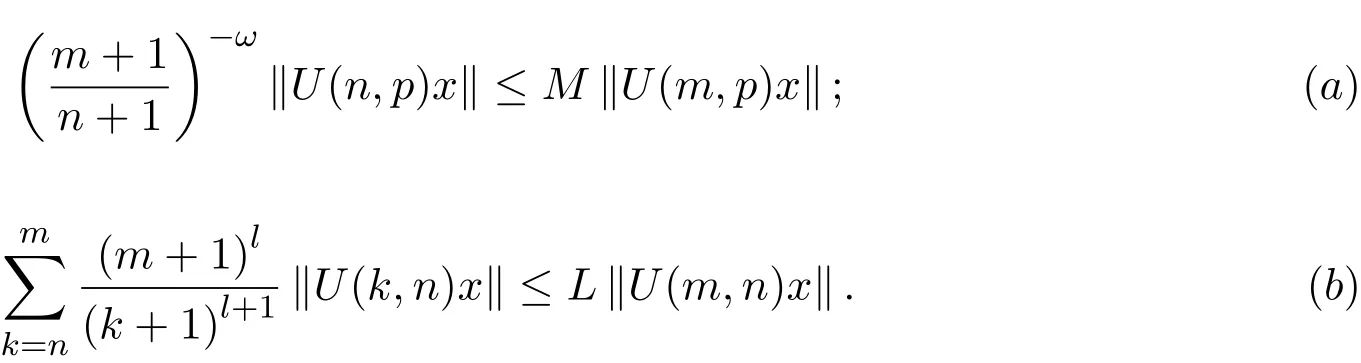
证明必要性.(a)式显然,下证(b)式.

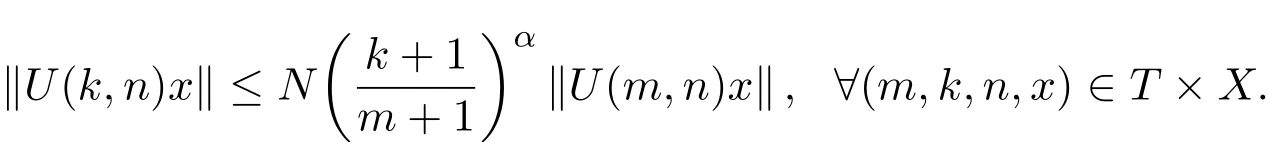
由此可得,

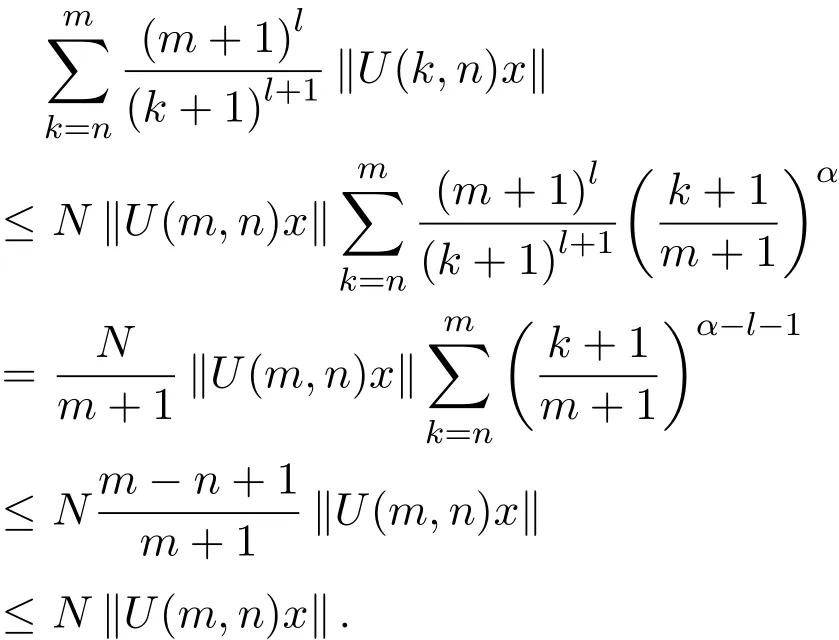
充分性.当m>2n时,则由条件可得,

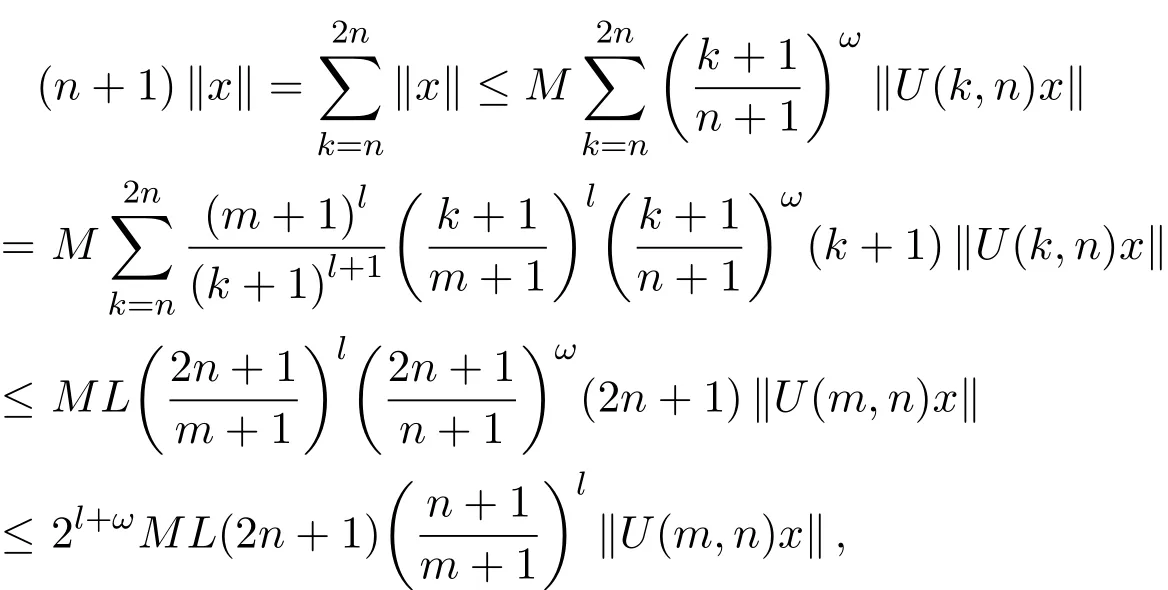
进而

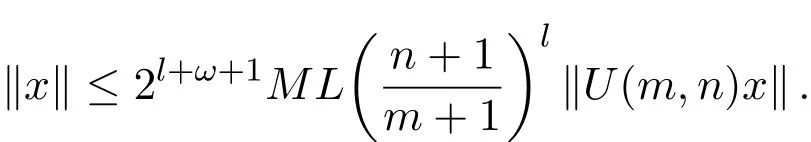
当2n≥m≥n时,则由(a)式可得,

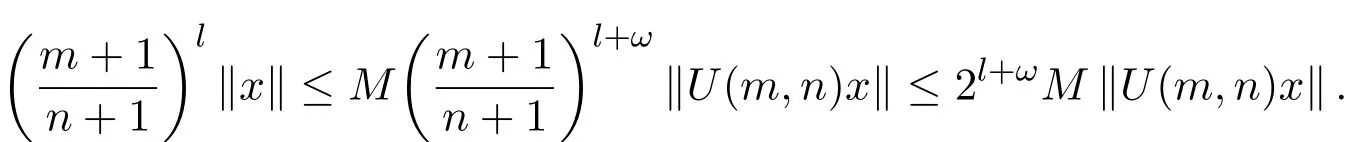
综上可知系统(1)是一致多项式膨胀的.

注3.1若线性离散时间系统(1)满足(a)式,则称其是多项式衰退的.

定理3.2具有多项式衰退的线性离散时间系统(1)是一致多项式膨胀的当且仅当存在一致多项式膨胀Lyapunov函数及常数K≥1,使得

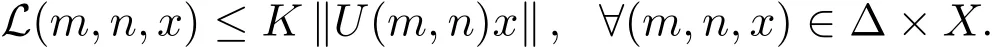
证明必要性.定义

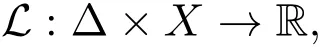
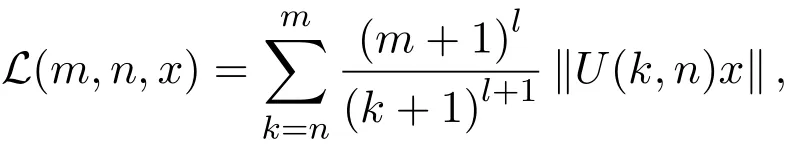
其中常数l由定义2.1给出.下证它为一致多项式膨胀Lyapunov函数.

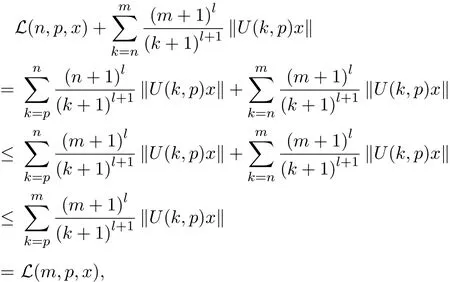
其中(m,n,p,x)∈T×X,m>n.

由定理3.1知,存在常数L≥1,使得

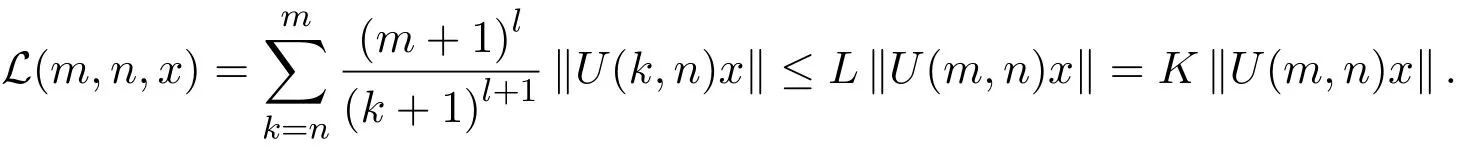
充分性.当n=p时,则由已知条件及一致多项式膨胀Lyapunov函数的定义可知,存在K≥1和µ>1,使得

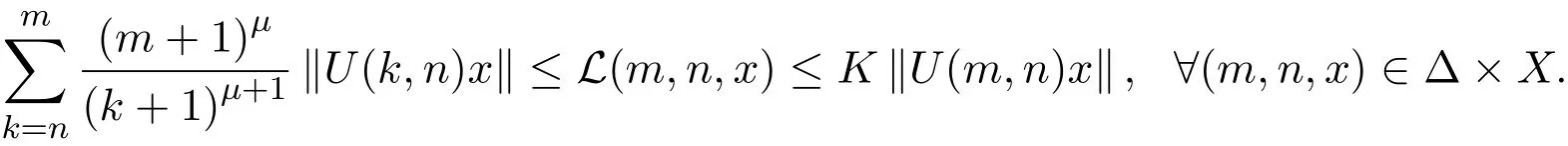
进而由定理3.1可得系统(1)是一致多项式膨胀的.

[1] Megan M,Sasu A L,Sasu B.Exponential instability of linear skew-product semi fl ows in terms of Banach function spaces[J].Result Math.,2004,45:309-318.

[2] Megan M,Sasu A L,Sasu B.Banach function spaces and exponential instability of evolution families[J]. Arch.Math.,2003,39:277-286.

[3] Megan M,Sasu A L,Sasu B.Exponential stability and exponential instability for linear skew-product fl ows[J].Math.Bohem.,2004,129:225-243.

[4] Megan M,Sasu A L,Sasu B.Perron conditions for uniform exponential expansiveness of linear skew-product fl ows[J].Monatsh.Math.,2003,138:145-157.

[5] Megan M,Sasu B,Sasu A L.Exponential expansiveness and complete admissibility for evolution families[J]. Czech.Math.J.,2004,54:1485-1493.

[6] Sasu B.New criteria for exponential expansiveness of variational di ff erence equations[J].J.Math.Anal. Appl.,2007,327:287-297.

[7] Yue T,Song X Q,Li D Q.On weak exponential expansiveness of evolution families in Banach spaces[J]. Sci.World J.,2013,2013(Article ID 284630):1-6.

[8] Yue T,Song X Q,Li D Q.On weak exponential expansiveness of skew-evolution semi fl ows in Banach spaces[J].J.Inequal.Appl.,2014,2014(Article 165):1-11.

[9] Popa I L,Ceau¸su T,Megan M.On exponential stability for linear discrete-time systems in Banach spaces[J]. Comput.Math.Appl.,2012,63:1497-1503.

[10] Popa I L,Megan M,Ceau¸su T.Exponential dichotomies for linear discrete-time systems in Banach spaces[J]. Appl.Anal.Discrete Math.,2012,6:140-155.

[11] Song X Q,Yue T,Li D Q.Nonuniform exponential trichotomy for linear discrete-time systems in Banach spaces[J].J.Func.Space Appl.,2013,2013(Article ID 645250):1-6.

[12] 岳田.几类演化型算子渐近行为的理论研究[D].徐州:中国矿业大学,2014.

[13] 岳田,宋晓秋,李志刚.n次积分C半群与抽象Cauchy问题的指数稳定性[J].河南大学学报:自然科学版, 2014,44(1):15-19.

[14] Barreira L,Valls C.Polynomial growth rates[J].Nonlinear Anal.,2009,71:5208-5219.

[15] Megan M,Ceau¸su T,Rˇamneant¸u M L.Polynomial stability of evolution operators in Banach spaces[J]. Opuscula Math.,2011,31:279-288.

[16] Megan M,Ceau¸su T,Minda A A.On Barreira-Valls polynomial stability of evolution operators in Banach spaces[J].Electron.J.Qual.Theo.Di ff er.Equat.,2011,33:1-10.

On uniform polynomial expansiveness of linear discrete-time systems in Banach spaces

Lei Guoliang1,Yue Tian1,Song Xiaoqiu2
(1.School of Science,Hubei University of Automotive Technology,Shiyan442002,China; 2.College of Science,China University of Mining and Technology,Xuzhou221008,China)

In this paper we study uniform polynomial expansiveness concept for linear discrete-time systems in Banach spaces.Our main objective is to give discrete characterizations for uniform polynomial expansiveness. As for applications we obtain a necessary and sufficient condition in terms of Lyapunov functions.Well-known results for uniform exponential stability,exponential expansiveness and polynomial stability are extended to the case of uniform polynomial expansiveness.

linear discrete-time systems,uniform polynomial expansiveness,Lyapunov function

O231

A

1008-5513(2014)05-0485-06

10.3969/j.issn.1008-5513.2014.05.008

2014-08-04.

国家自然科学基金(51374199);中央高校基本科研业务费专项资金(2012LWB53).

雷国梁(1971-),硕士,讲师,研究方向：应用数学.

2010 MSC:34D20,34D05