完全五部图的S-整图性研究

赵宁,吴廷增

(青海民族大学数学与统计学院,青海西宁810007)

完全五部图的S-整图性研究

赵宁,吴廷增

(青海民族大学数学与统计学院,青海西宁810007)

应用矩阵的初等变换得到了完全五部图的Seidel多项式,并给出了完全五部图是S-整图的一个充分必要条件.进一步刻画了完全正则五部图和两类特殊完全五部图的Seidel谱.

Seidel多项式;Seidel谱;S-整图;完全五部图

1 引言

本文涉及的图都是简单图,未定义的术语和符号见文献[1].设G=(V(G),E(G))是n个顶点的图.A(G)表示图G的(0,1)-邻接矩阵.称S(G)=J−I−2A(G)是图G的Seidel矩阵,其中J是全1-矩阵,I是单位矩阵.多项式SG(λ)=det(λI−S(G))称为图G的Seidel特征多项式(简记为Seidel多项式).由代数基本定理可知,SG(λ)=0至多有n个特征根.设λ1,λ2,···,λi是SG(λ)的i(1≤i≤n)个不同的特征根,且它们的重数依次为k1,k2,···,ki,定义为图G的Seidel 谱.

如果图G的Seidel多项式的所有特征根都是整数,则称G是S-整图.1974年,文献[2]中首次提出了哪些图是整图,该问题的提出,引起了国内外许多学者的关注,得到了许多重要的结论.2002年,文献[3]给出了一个全面的综述,并指出该问题的研究是非常困难的.近年来,一些关于图其它形式的矩阵相对应的整图刻画被研究,如:拉普拉斯矩阵、无符号拉普拉斯矩阵、Seidel矩阵等(参见文献[4-12]).特别地,文献[13]中构造了整的完全四部图,文献[14]中给出了完全三部图是整图的充要条件.

令Kn1,n2,··,nt是完全t部图,

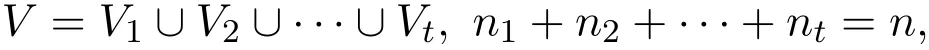
这里Vi是非空且两两不相交的点集.为了方便,设|Vi|=ni(i=1,2,···,t).

如果n1=n2=···=nt=n,则称为完全正则t部图.文献[3]对图G的Seidel谱给出了一些初步结果,迄今关于S-整图方面的研究不是很多.本文探讨了完全多部图是S-整图的一些结果,证明了完全五部图是S-整图的一个充要条件,以及几类特殊完全五部图是整图的优美结果.

2 主要结果及其证明

为了证明后面的主要定理,给出下面的引理.

引理2.1设G是完全五部图Kn1,n2,··,n5,则G的Seidel多项式

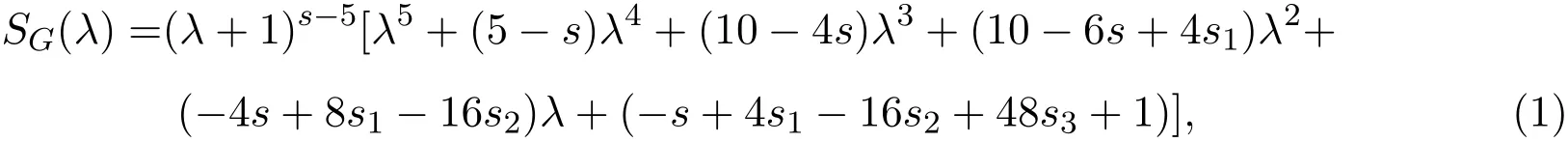
其中

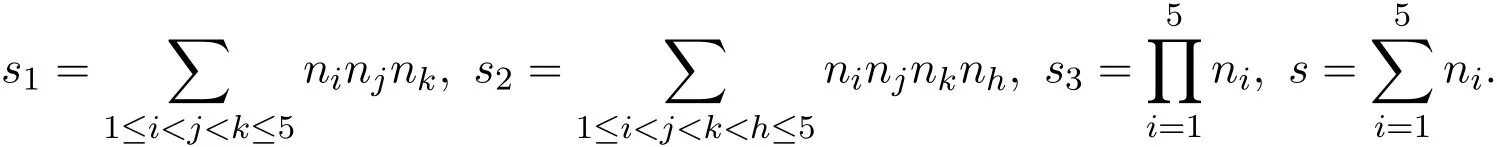
证明设G是完全五部图Kn1,n2,··,n5,由定义知,

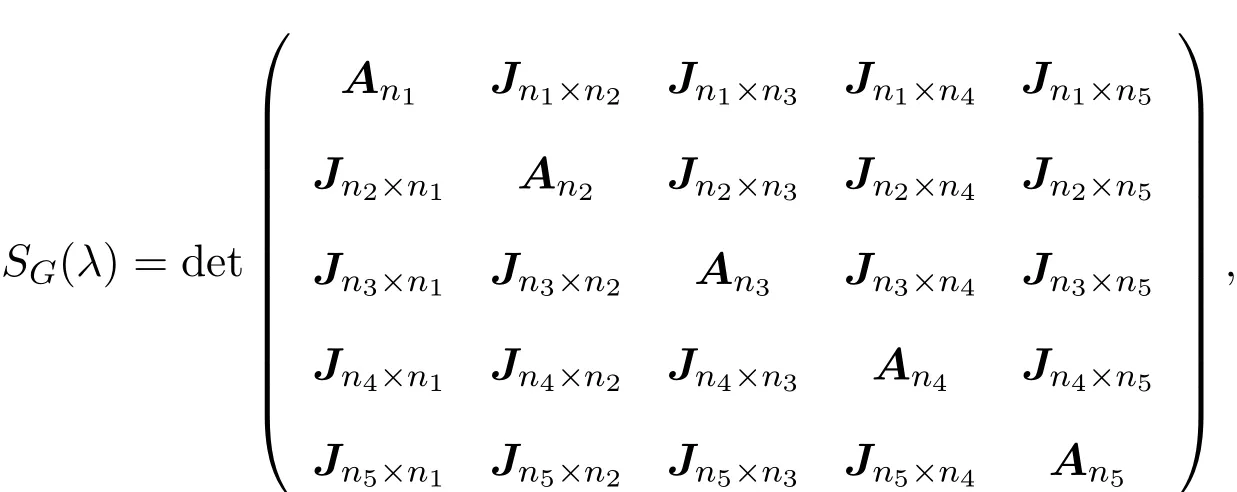
其中Jni×nj是ni×nj(i̸=j)阶全1矩阵;Ani是主对角元素为λ,其余元素为−1的ni阶方阵(i,j=1,2,···,5).

对SG(λ)施行变换:

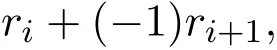
i的取值依次为:

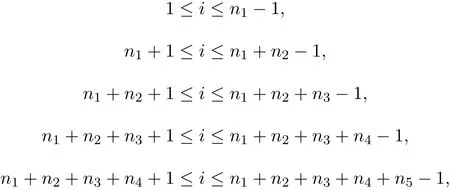
经过上述运算,得到

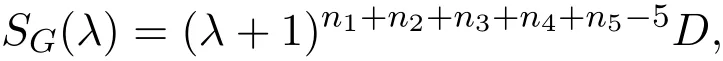
其中

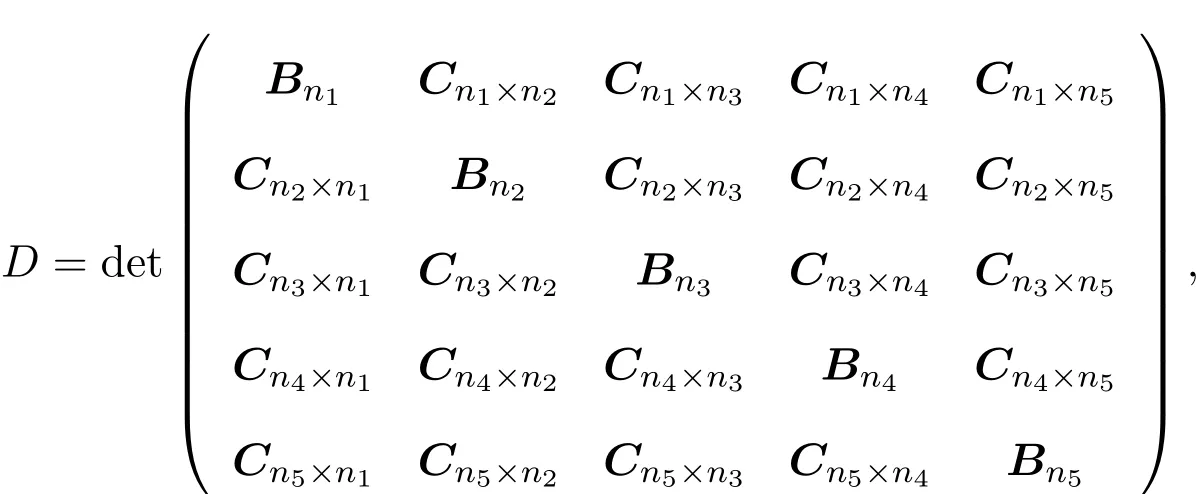
其中Bni是ni阶方阵(i=1,2,···,5),且

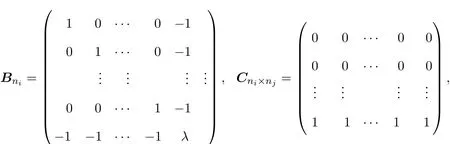
其中i,j=1,2,···,5,i̸=j.

进一步,对D施行如下变换:rn1+rn1−1+rn1−2+···+r1,rn1+n2+rn1+n2−1+rn1+n2−2+···+ rn1+1,···,rn1+n2+n3+n4+n5+rn1+n2+n3+n4+n5−1+rn1+n2+n3+n4+n5−2+···+rn1+n2+n3+n4+1,得到

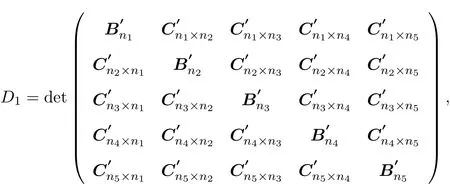
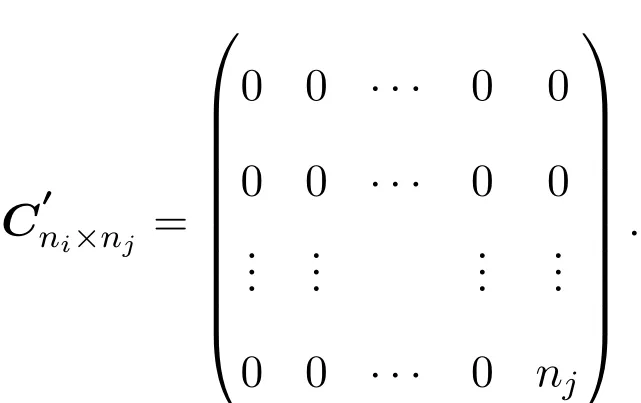
对D1进一步化简可得:

其中

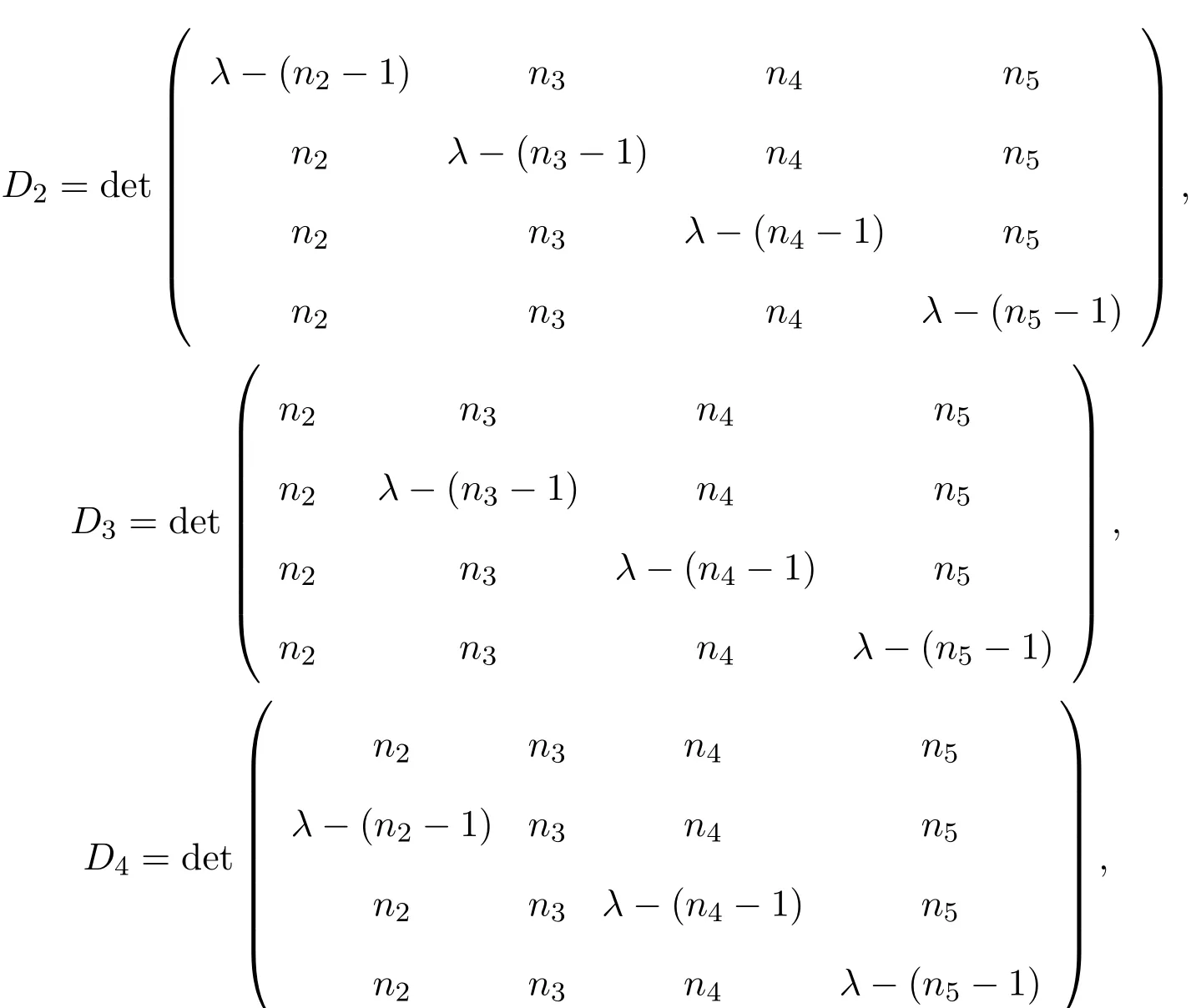
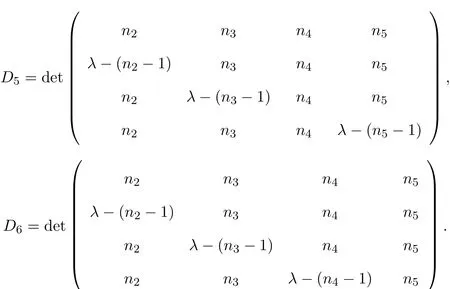
对Di(i=3,4,5,6)施行变换:第一行乘以−1加到其余各行,然后将Di(i=3,4,5,6)按第i−3列展开,得到:

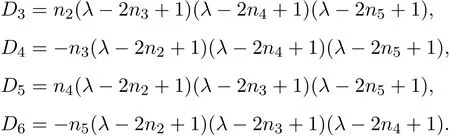
将D2按第一列展开,得

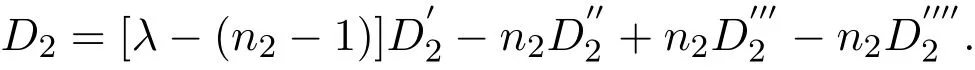
用计算Di(i=3,4,5,6)类似的方法计算并逐步回代,最终可得图G的Seidel多项式为(1)式.

定理2.2设G是完全五部图Kn1,n2,··,n5,则G是S-整图当且仅当的所有根是整数.

证明由引理2.1知,完全五部图G的Seidel多项式为(1)式.要使(1)的所有根是整数,

由定理2.2可推导出以下结果:

推论2.3完全五部图G=Kn,n,n,n,n是S-整图,且

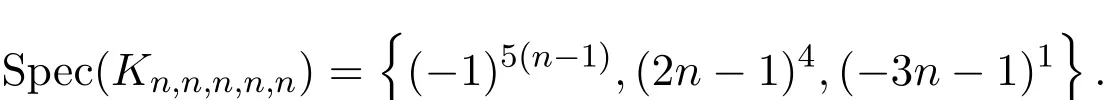
证明将(1)式中的ni(i=1,2,···,5)都替换为n,得到

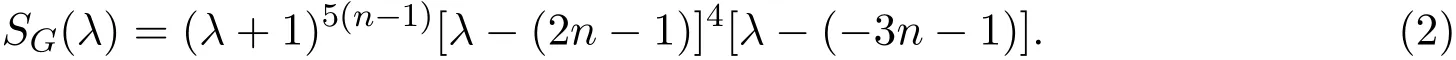
显然SG(λ)=0的根为(−1)6(n−1),(2n−1)5,(−4n−1)1,从而

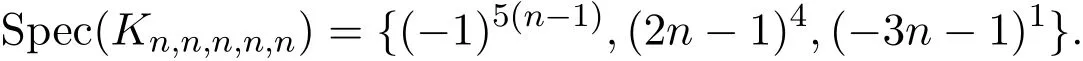
推论2.4完全图K5的Seidel谱Spec(K5)={14,(−4)1}.

证明取推论2.3中的n=1,便是完全图K5.由(2)式得其谱Spec(K5)={14,(−4)1}.

推论2.5设G是完全五部图Km,n,n,n,n,那么

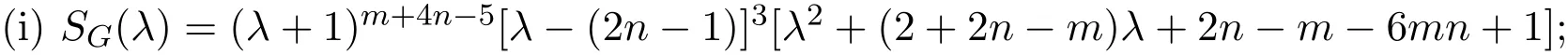
(ii)G是S-整图的充分必要条件是(2n+m)+16mn是整数且与m同为奇数或同为偶数.

证明(i)由引理2.1,将Kn1,n2,··,n5中的n1,n2,n3,n4,n5用m,n,n,n,n替代,则相应的完全五部图Km,n,n,n,n的Seidel多项式为:

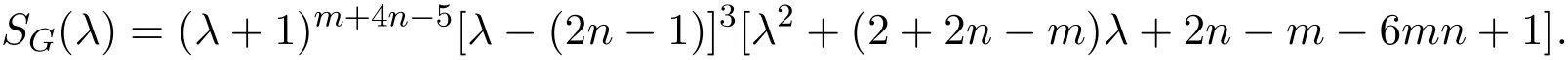
(ii)令

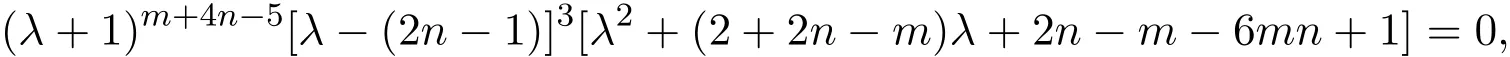
要使所有根都是整数,只需

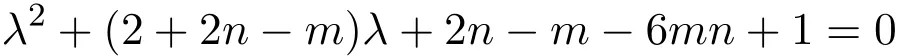
的根是整数,由求根公式即可得证.

推论2.6设G是完全五部图Km,m,n,n,n,那么

(i)SG(λ)=(λ+1)2m+3n−5[λ−(2n−1)]2[λ−(2m−1)][λ2+(n+2)λ+n−6mn+1];

证明(i)由引理2.1,将Kn1,n2,··,n5中的n1,n2,n3,n4,n5用m,m,n,n,n替代即可.

(ii)与推论2.5的(ii)式的证明类似.

3 结束语

本文应用矩阵行初等变换,计算了完全五部图G=Kn1,n2,··,n5的Seidel多项式,并给出了图G是S-整图的一个充分必要条件.并对当{n1,n2,···,n5}是由2个不同的正整数构成时,刻画了对应的完全五部图的整图性问题.当n1,n2,n3,n4,n5是由3个或4个正整数构成时,对应的完全五部图的整图性问题的讨论就显得比较繁琐,更简便的办法,值得继续探讨.

[1] Cvetkovi´c D,Doob M,Sachs H.Spectra of Graphs[M].New York:Academic press,1980.

[2] Harary F,Schwenk A J.Which graphs have integral[M]//Graphs and combinatorics.Berlin:Springer,1974.

[3] Bali´nska K T,Cvetkovi´c D,Radosavljevi´c Z,et al.A survey on integral graphs[J].Univ.Beograd.Publ. Elektrotehn.Fak.Ser.Mat.,2002,13:42-65.

[4] Lu Shifang,Zhao Haixing.Singless Laplacian characteristic polynomials of complete multipartite graphs[J]. Chinese Quarterly Journal of Mathematics,2012,27(1):36-40.

[5] Wang Ligong,Liu Xiaodong.Integral complete multipartite graphs[J].Discrete Math.,2008,308:3860-3870.

[6] Simi´c S K,Stanic Z.Q-integral graphs with edge-degrees at most fi ve[J].Discrete Math.,2008,308:4625-4634.

[7] Stani´c Z.Some results on Q-integral graphs[J].Ars Combin.,2009,90:321-335.

[8] Kirland S.Constructably laplacian integral graphs[J].Linear Algebra Appl.,2007,423:3-21.

[9] 赵国鹏,王力工.完全多部图的拉普拉斯特征多项式[J].纺织高校基础科学学报,2011,24(2):243-245.

[10] 卢世芳,卫良,赵海兴.完全3-部图的无符号Laplace谱[J].山东大学学报:理学版,2012,47(12):41-47.

[11] 谭尚旺.矩阵特征多项式的图论计算公式[J].纯粹数学与应用数学,2009,25(2):12-18.

[12] 王龙芹,橝江华,秦峰.围长为r的n阶本原有向图的点指数[J].纯粹数学与应用数学,2010,26(4):72-81.

[13] H´ıc P,Pokom´y M.Integral complete 4-partite graphs[J].Discrete Math.,2008,308:3704-3705.

[14] H´ıc P,Pokom´y M.New sufficient conditions for integral complete 3-partite graphs[J].Applicable Analysis and Discrete Mathematics,2008,2:276-284.

A study of S-integral graph of complete 5-partite graphs

Zhao Ning,Wu Tingzeng
(School of Mathematics and Statistics,Qinghai Nationalities University,Xining,Qinghai,810007,China)

By elementary transformation of a matrix,we compute the Seidel polynomial of complete 5-partite graph,and give a necessary and sufficient condition for a complete 5-partite graph to be an S-integral graph. Furthermore,we characterize the Seidel spectra of a complete regular 5-partite graph and two classes of complete 5-partite graphs with special structure,respectively.

Seidel polynomial,Seidel spectrum,S-integral graph,complete 5-partite graphs

O157.5

A

1008-5513(2014)05-0467-07

10.3969/j.issn.1008-5513.2014.05.005

2014-06-17.

青海省自然科学基金(2011Z911).

赵宁(1974-),硕士,副教授,研究方向：图的谱理论.

2010 MSC:05C78