广义Pell方程Ax2−By2=4的通解公式

史保怀,李小雪

(1.陕西学前师范学院数学系,陕西西安710100;2.西北大学数学学院,陕西西安710127)

广义Pell方程Ax2−By2=4的通解公式

史保怀1,李小雪2

(1.陕西学前师范学院数学系,陕西西安710100;2.西北大学数学学院,陕西西安710127)

主要运用Lucas数的奇偶性,讨论了当A,B是适合A>1,2-AB且AB非平方数的正整数时,广义Pell方程的整数解(x,y),即给出了方程Ax2−By2=4适合gcd(x,y)=1的整数解(x,y)的通解公式.

二元二次Diophantine方程;通解公式;Lucas数的奇偶性

1 引言

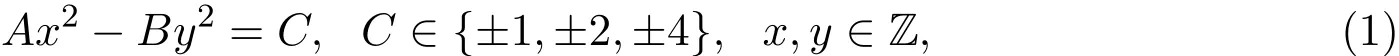
的二元二次Diophantine方程统称为广义Pell方程,其性质是数论中的一个基本而又重要的研究课题[1-11].

本文将对A>1,2-AB且C=4的情况讨论方程(1)满足gcd(x,y)=1的解(x,y)的通解公式.此时,方程(1)可表成:

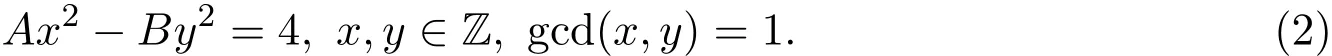
由文献[3]第1.3节可知:如果方程(2)有解(x,y),则它必有唯一的正整数解(x1,y1)满足:

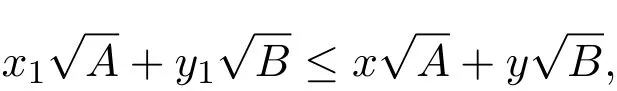
这里的(x,y)过该方程的所有正整数解.如此的(x1,y1)称为方程(2)的最小解.方程(2)的任何一组解(x,y)都可表成:

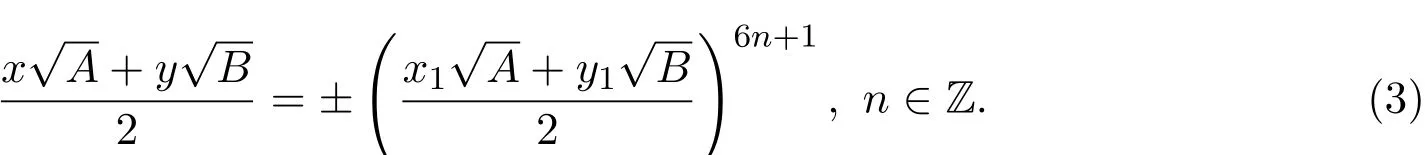
然而,方程(2)的通解公式(3)是错的.例如,当A=7且B=3时,方程(2)有解(x,y),而且它的最小解是(x1,y1)=(1,1).此时,(x,y)=(19,29)是方程(2)的一组解,但是由于

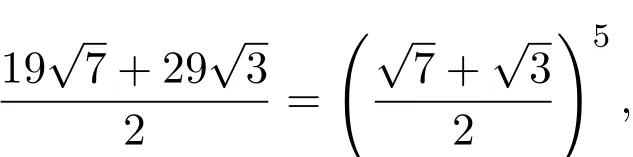
所以该解不能表成(3)式.

本文运用Lucas数的奇偶性给出了方程(2)正确的通解公式,即证明:

定理1.1当A,B是适合A>1,2-AB且AB非平方数时,如果方程(2)有解(x,y),则它的任何一组解(x,y)都可表成

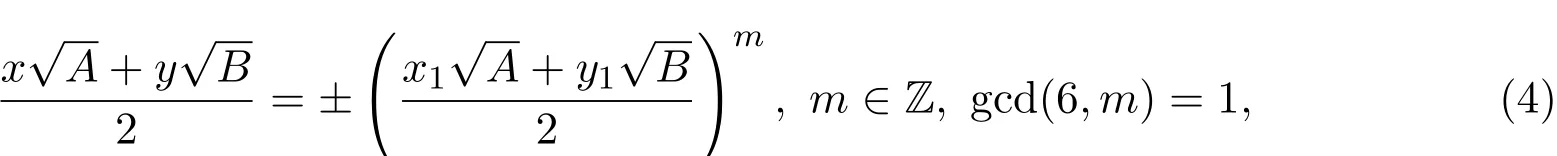
其中(x1,y1)是方程(2)的最小解.

2 若干引理

引理2.1对于正整数t以及复数α和β,

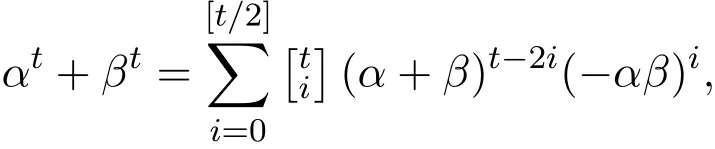
其中[t/2]是t/2的整数部分,

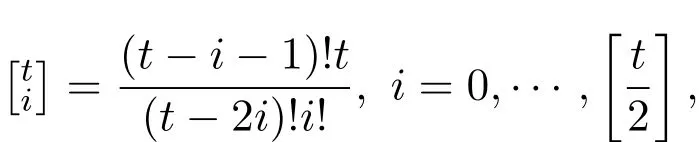
都是正整数.

证明参见文献[12]的(1.76)式.

引理2.2对于正整数t,设Lt是第t个Lucas数.

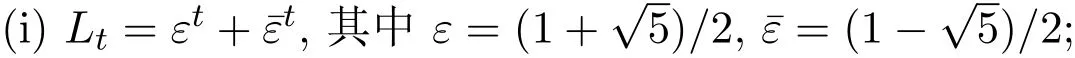
(ii)如果3|t,则Lt是偶数;如果3-t,则Lt是奇数.

证明参见文献[1]的第4.2节.

引理2.3对于正整数t,设

证明由引理2.1可知(i=0,···,[t/2])都是正整数,所以由(5)式可知f(t)都是整数.

由引理2.2的结论(i)可知,

因为由(7)式可知α+β=3且αβ=1,所以根据引理2.1,由(6)式可得,

又因3≡1(mod 2),故由(5)式和(8)式可得,

于是,根据引理2.2的结论(ii),由(9)式即得本引理.

设A,B是适合A>1,2-AB,gcd(A,B)=1且AB非平方数的正整数.

引理2.4方程

有适合v̸=0的解(u,v),而且有唯一的正整数解(u,v)满足这里的(u,v)过该方程所有的正整数解.如此的(u1,v1)称为方程(10)的最小解.

证明参见文献[3]的定理1.1.1.

引理2.5方程

必有适合V̸=0的解(U,V),而且有唯一的正整数解(U,V)满足U+V这里的(U,V)

1111过该方程的所有正整数解.如此的(U1,V1)称为方程(11)的最小解.

(i)方程(10)的最小解(u1,v1)满足

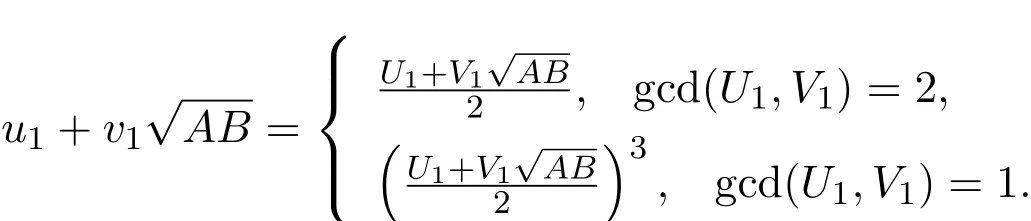
(ii)方程(11)的任何一组解(U,V)都可表成

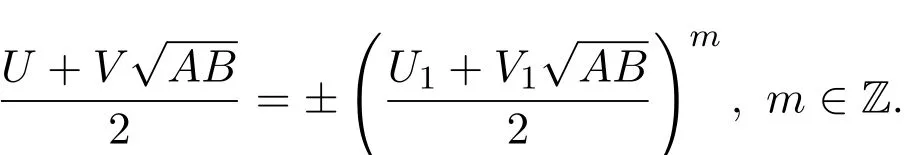
证明参见文献[3]的定理1.1.6.

引理2.6方程(11)有适合gcd(U,V)=1的解(U,V)的充要条件是该方程的最小解(U1,V1)适合gcd(U1,V1)=1.

证明充分性易证.以下证明其必要性.当方程(11)有适合gcd(U,V)=1的解(U,V)时, U和V必定都是奇数.此时,如果gcd(U1,V1)̸=1,则gcd(U1,V1)=2,并且由引理1.5的结论(i)和结论(ii)可得:

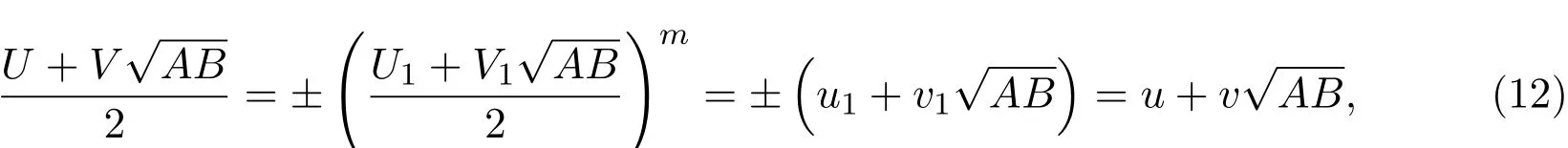
其中(u1,v1)是方程(10)的最小解,u和v都是整数.然而,由(12)式可知U=2u且V=2v,故有gcd(U,V)>1这一矛盾.由此可知,此时gcd(U1,V1)=1.

引理2.7如果方程(11)有适合gcd(U,V)=1的解(U,V),则该方程的任何一组适合此条件的解(U,V)都可表示成:

其中(U1,V1)是方程(11)的最小解.

证明由于当(U,V)是方程(11)的解时,(|U|,|V|)也是它的解;而且该方程的最小解(U1,V1)满足

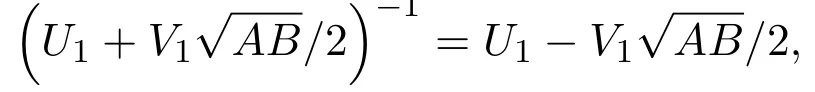
所以只需讨论该方程的正整数解即可.

设(U,V)是方程(11)的一组适合gcd(U,V)=1的正整数解.此时,U和V都是奇数,由引理2.6可知此时gcd(U1,V1)=1,所以U1和V1也是奇数.

根据引理2.5可知:

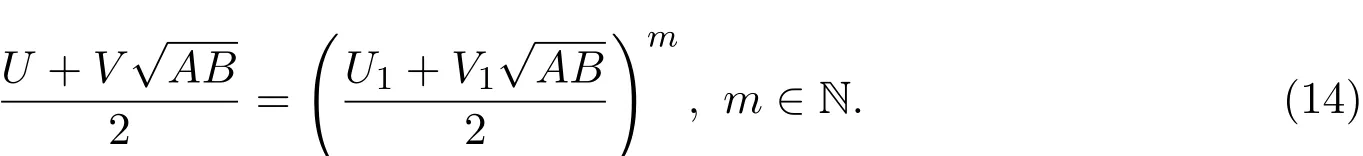
设

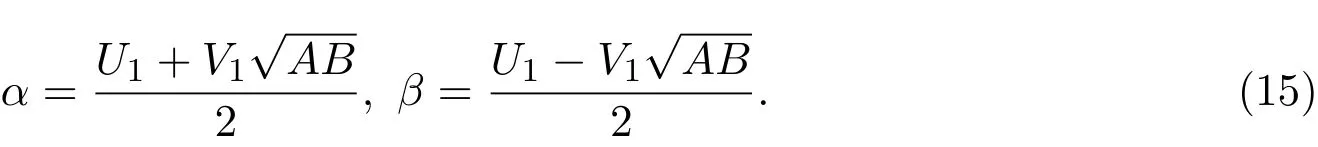
根据引理2.1,由(14)式和(15)式可得,

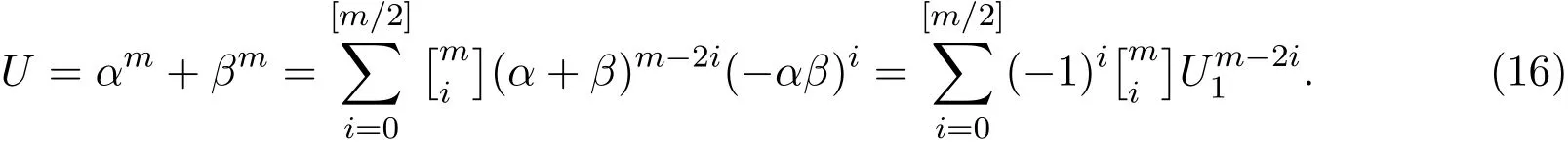
因为U1是奇数,U1≡1(mod 2),所以由(15)和(16)式可得,

由于U是奇数,所以根据引理1.3,由(17)式可知3-m.于是,由(14)式可知引理成立.

引理2.8如果方程(2)有解(x,y),则方程(10)的最小解(u1,v1)满足:

其中(x1,y1)是方程(2)的最小解.

证明参见文献[3]的定理1.3.3.

3 定理1.1的证明

显然,若能证明方程(2)的任何一组正整数解(x,y)都可表成

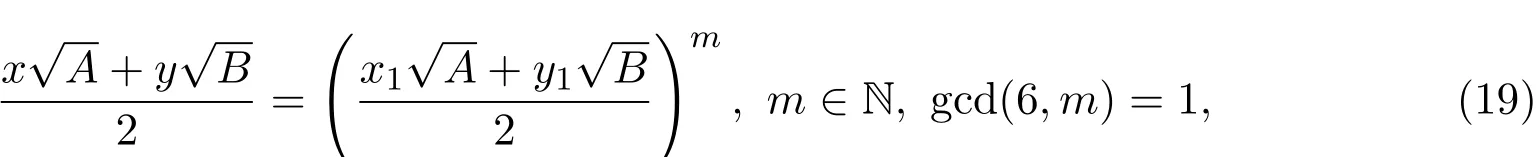
则定理1.1成立.

设(x,y)是方程(2)的一组正整数解,又设

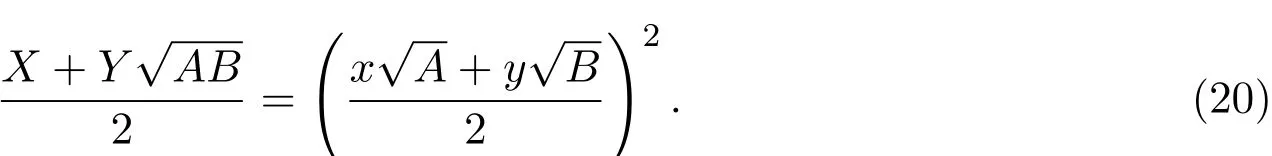
因为由(2)式和(20)式可知

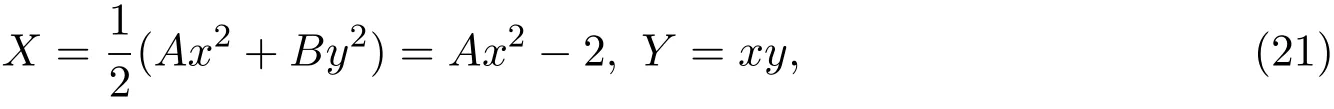
X和Y都是正奇数,所以(U,V)=(X,Y)是方程(11)的一组适合gcd(U,V)=1的正整数解.因此,根据引理2.7,由(20)式可得

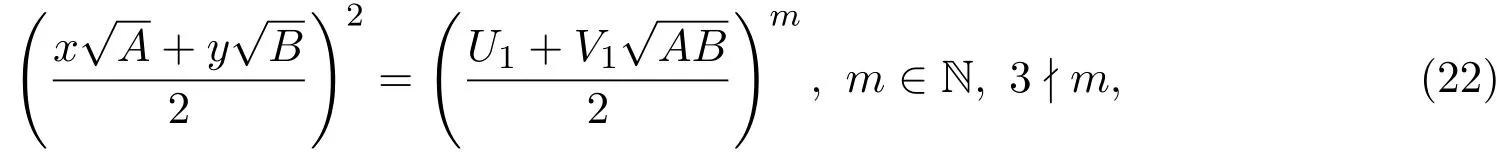
其中(U1,V1)是方程(11)的最小解.

此时方程(11)有适合gcd(U,V)=1的解(U,V),则由引理2.6可知,

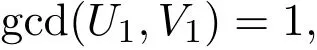
另外,由引理2.8可知(u1,v1)满足(19)式,故由(19)和(23)式可得,

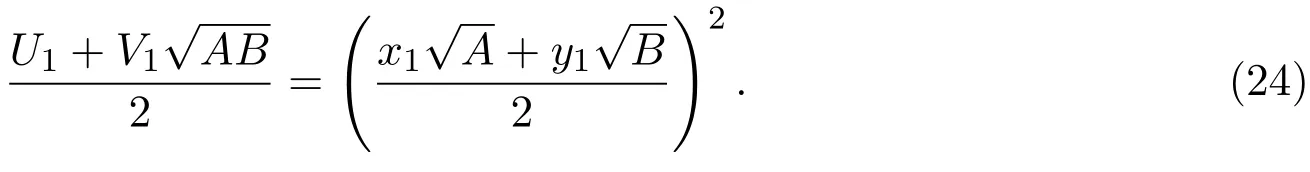
于是,将(24)式代入(22)式即得,

又因A>1,所以由(24)式可知(25)式中m不能是偶数,故由(25)式可得(19)式.

又由引理2.5可知,方程(10)的最小解(u1,v1)满足

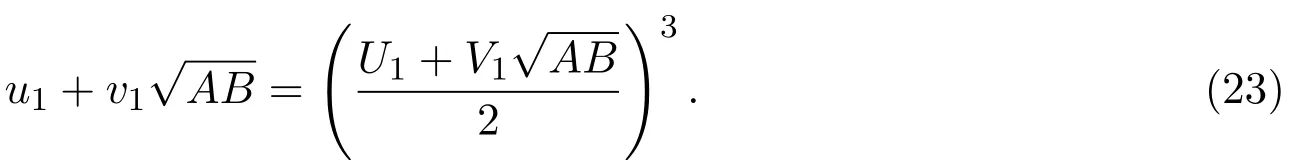
参考文献

[1] 柯召,孙琦.谈谈不定方程[M].上海:上海教育出版社,1980.

[2] 曹珍富.丢番图方程引论[M].哈尔滨:哈尔滨工业大学出版社,1989.

[3] 曹珍富.不定方程及其应用[M].上海:上海交通大学出版社,2000.

[4] 张文鹏,李海龙.初等数论[M].西安:陕西师范大学出版社,2008.

[5] 乐茂华.Pell方程组x2−ay2=1和z2−by2=1的解数[J].数学进展,2005,34(1):106-116.

[6] 林炳生.佩尔方程的最小正整数解[J].数学的实践与认识,2011,41(8):130-145.

[7] 吴莉,王学平,杨仕椿.Pell方程x2−Dy2=±2的解的递推性质[J].四川师范大学学报:自然科学版,2013, 36(2):190-192.

[8] 管训贵.关于Pell方程x2−2y2=1与y2−Dz2=4的公解[J].华中师范大学学报:自然科学版,2012, 46(3):267-268.

[9] 陈申宝,陈廷键.x2+y2=N2正整数解的结构与求法[J].纯粹数学与应用数学,2013,29(1):50-59.

[10] 陈永高．Pell方程组x2−2y2=1与y2−Dz2=4的公解[J].北京大学学报:自然科学版,1994,30(3):298-302．

[11] 杨克仁,徐研.广义Pell方程及其应用[J].数学研究,1995,3(28):89-92.

[12] Lidl R,Niederreiter H.Finite Fields[M].MA:Addison-Wesley,1983.

The general solution formula of the generalized Pell equation
Ax2−By2=4

Shi Baohuai1,Li Xiaoxue2
(1.Department of Mathematics,Shaanxi Xuqian Normal University,Xi′an710100,China; 2.School of Mathematics,Northwest University,Xi′an710127,China)

The main purpose of this paper is using the parity of Lucas numbers,to discuss the integer solutions (x,y)of the equation when A,B be positive integers such that A>1,2-AB,and AB is not a complete square,which gives a general solution formula of integer solutions(x,y)of the equation Ax2−By2=4 with gcd(x,y)=1.

binary quadratic diophantine equation,general solution formula,parity of Lucas number

O156.7

A

1008-5513(2014)05-0441-06

10.3969/j.issn.1008-5513.2014.05.001

2014-06-01.

国家自然科学基金(11371291);陕西学前师范学院科研基金(11KJ003).

史保怀(1963-),教授,研究方向：数论.

2010 MSC:O156.7