硅微陀螺正交误差直流校正设计与分析
2014-07-19倪云舫李宏生黄丽斌赵立业
倪云舫,李宏生,杨 波,黄丽斌,赵立业,王 攀,刘 嘉
(东南大学 仪器科学与工程学院 微惯性仪表与先进导航技术教育部重点实验室,南京 210096)
硅微陀螺正交误差直流校正设计与分析
倪云舫,李宏生,杨 波,黄丽斌,赵立业,王 攀,刘 嘉
(东南大学 仪器科学与工程学院 微惯性仪表与先进导航技术教育部重点实验室,南京 210096)
为硅微陀螺设计了一种正交误差直流校正方法,通过设计校正结构和加载直流电压实现正交校正。建立了存在正交误差时敏感质量的运动微分方程,分析明确了正交响应的成因和对驱动运动轨迹的影响。为硅微陀螺设计了正交校正结构,实现构建静电耦合弹性系数并利用驱动运动产生校正静电力。校正力的频率和相位无需电路控制,使该方法相较于传统校正方法具备特殊优势。设计并分析了校正电压的两种加载方式,通过实验测试验证了正交响应幅值随校正电压的变化规律。实测校正电压接近理论值,证明了校正结构设计的正确性。该方法在双线振动式硅微陀螺中具有重要应用价值。
硅微陀螺;正交误差;正交校正;直流电压;结构设计
硅微陀螺基于硅微机械加工工艺制造,因其相较于传统陀螺体积小、功耗低、可量产等优势,在商业和军事领域均有广泛应用[1-3]。硅微陀螺为哥氏振动陀螺的一种,利用哥氏效应使驱动振动耦合到检测方向进行角速度检测。然而,由于加工误差等非理想因素的存在,驱动方向和检测方向的运动之间还存在其他耦合机制,如弹性耦合、阻尼耦合、静电耦合等,使得在没有角速度输入的情况下,硅微陀螺的检测方向仍有振动信号输出,直接影响其零偏稳定性和零偏温度稳定性等关键性能。由于硅微陀螺的弹性梁对加工误差十分敏感,弹性耦合一般最为严重,其造成的检测振动与哥氏效应引起的检测振动在相位上相差90°,故被称为正交误差[4]。正交误差通常远大于有用信号,其校正为硅微陀螺研制中的关键技术之一[5]。目前常用的校正方法有同步解调法和闭环抑制法两种[6]。前者利用与有用信号同频同相的电压信号对输出信号进行解调,从而消除输出中与有用信号相位相差 90°的正交信号。后者通过设计闭环反馈控制回路,产生与引起正交信号的弹性耦合力同频反相的反馈力抑制正交运动,从而从源头上消除正交信号。采用同步解调法时,正交信号仍然存在,其相对于有用信号而言很大的幅值增加了对前端电路动态范围的要求,限制了陀螺的分辨率和信噪比。闭环抑制法从源头上消除了正交运动,对前端电路的限制放宽,但与同步解调法需要精确的解调电压相位控制类似,闭环抑制法需要精确的反馈力相位控制。两种方法都对电路的相位精度提出了很高的要求,尤其当环境变化造成陀螺结构参数和电路器件参数变化时更为困难。
针对以上问题,本文在硅微陀螺设计中采用了一种正交误差直流校正方法[7-8],通过设计专用的校正结构产生校正静电力抵消弹性耦合力,从而抑制正交运动。校正力的幅值由加载的直流电压控制,频率和相位信息由驱动振动直接提供,无需专门的控制电路。该法对前端电路动态范围和电路相位精度均无特殊要求,具备实用价值。
1 正交误差对敏感质量运动的影响分析
存在弹性耦合时,硅微陀螺敏感质量的二维运动微分方程可表示为:

式中,mc为敏感质量,cx、cy、kx、ky分别为驱动方向(X向)和检测方向(Y向)的阻尼、弹性系数,kxy、kyx为驱动和检测方向之间的耦合弹性系数;Fd为简谐静电驱动力,幅值和角频率分别为F0和ωd;Fc为哥氏力,Ωz为输入角速度(Z向)。
一般而言,模态不匹配时,检测振幅远小于驱动振幅,故kxy的影响可忽略不计。弹性耦合对敏感质量运动的影响主要表现为kyx与驱动位移x结合构成作用于检测方向的弹性耦合力Fq,其频率和相位与x一致,故与哥氏力Fc同频且相位相差90°,定义为正交力。
硅微陀螺工作时,敏感质量沿驱动方向恒幅谐振,定义振幅为Ad,则x、Fq、Fc可表示为:
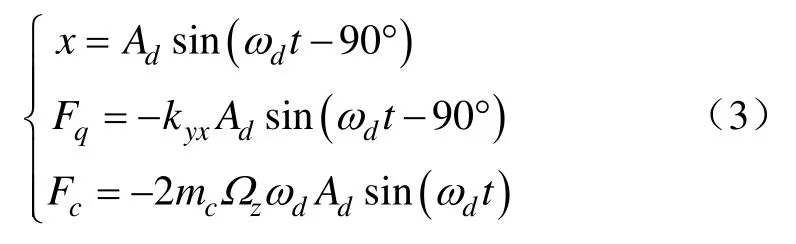
定义正交力Fq、哥氏力Fc引起的敏感质量沿检测方向的位移响应分别为正交响应yq和哥氏响应yc,有:

式中,ωy、Qy分别为检测模态的谐振频率和品质因数。可见,yq和yc相较于Fq和Fc存在同样的相移φ,仍为同频且相位相差90°。正交误差等效角速度Ωq可表示为:

假设驱动频率为4 kHz,Qy在几千量级,Ωz=0 (°)/s,存在Ωq=100 (°)/s时,敏感质量质心的运动轨迹如图1所示。

图1 存在正交误差时敏感质量质心的运动轨迹Fig.1 Motion trajectory of the center of proof mass when quadrature error exists
可见,正交误差的存在使得敏感质量的驱动运动偏离理想的X向,并且由于yq和x之间相差φ的存在,呈现椭圆形运动轨迹。耦合弹性系数kyx不变时,一定的驱动频率条件下,检测与驱动模态的频差Δf越小,正交响应yq的幅值越大,yq和x之间的相差φ也越大。yq的幅值由Y向检测电极提取后,成为陀螺输出中的正交信号。可见正交信号与有用信号类似,是一个动态信号,其幅值和相位同样受到固有频率、Q值等结构参数的影响,因而在环境变化导致结构参数波动时,正交信号也将发生变化,从而使相位控制成为应用同步解调法和正交抑制法进行正交校正时的一个难点。正交误差直流校正方法可以缓解这一问题。
2 正交误差直流校正结构设计与分析
正交误差直流校正的原理为,通过设计校正结构,构建如下作用于敏感质量的Y向校正静电力:

式中,keyx为静电耦合弹性系数,其符号和大小由校正结构与所加直流电压共同决定。驱动位移x为机械信号,由敏感质量的驱动运动直接提供给校正结构,因此无需进行频率和相位控制。比较式(3)(6)可见,校正力Fey与正交力Fq的形式一致,当构建的静电耦合弹性系数keyx与结构耦合弹性系数kyx等值反号时,Fey实现对Fq的平衡,从而抑制正交运动,实现正交校正。
本文在自主研制的某型双质量硅微陀螺[9]上设计了校正结构,并完成了第一回合的制版加工。包含校正结构的硅微陀螺结构示意图及校正结构的局部电镜照片如图2所示。

图2 双质量硅微陀螺结构示意图及校正结构局部照片Fig.2 Structure of the dual-mass silicon micro-gyroscope and a local SEM photo of the quadrature correction structure
该陀螺结构为全解耦形式,包含驱动框架、敏感质量、检测框架三部分质量,驱动框架和检测框架分别只具备X向、Y向自由度,敏感质量具备X、Y两向自由度,实现利用哥氏效应检测Z向角速度。
校正结构主要由布置于敏感质量中轴线两侧的不等间隙梳齿构成,初始的大、小间隙分别为pd0和d0。可动梳齿位于敏感质量上,左右梳齿对称布置。固定梳齿连接于两组校正电极A和B上,分别施加有直流电压VA和VB,左右梳齿根据大、小间隙的Y向位置反对称布置。单组校正结构由4个可动梳齿和相应的固定梳齿构成,此种组合方式的设计目的在于消除伴随校正静电力同时出现的附加干扰静电力。敏感质量的Y向位移很小(y< 式中,Fex、Fey分别为X、Y向静电力,kexx、keyy分别为X、Y向静电弹性系数,kexy、keyx为两个方向之间的静电耦合弹性系数。 校正结构对敏感质量运动的影响主要表现为构建静电耦合弹性系数keyx,结合位于敏感质量上的可动梳齿的驱动运动x,形成作用于Y向的校正静电力Fey,用于平衡引起正交误差的正交力Fq。keyx的大小由校正结构参数n、h、d0、p和所加直流电压VA、VB的平方差决定,正、负符号由VA、VB的相对大小决定。结合式(3)(5)(7)可知,校正等效角速度为Ωq的正交误差所需的直流电压加载条件为: 另外,由式(8)可见,校正结构同时也产生Y向静电弹性系数keyy,影响检测模态的谐振频率。根据目的不同,可对keyy的大小进行相应设计上的调节。对照keyx和keyy的表达式可见:若希望正交校正对检测模态谐振频率的影响最小化,可在设计中令校正结构梳齿的交叠长度l0尽可能小,并在结构模态设计中将正交校正引起的频差变化纳入考量;若希望利用keyy进行检测频率调节,则可适当增大l0的设计值,并对直流电压VA、VB的加载方式进行相应的优化设计。 正交校正过程中,校正电压的调节依赖于正交响应yq与所加直流电压VA、VB的相对变化规律。校正结构对敏感质量检测方向运动微分方程的影响主要表现为引入静电弹性系数keyx和keyy,即有: 求解该式可得此时的正交响应yq为: 对于图2所示的校正结构,若记: 则静电弹性系数keyx和keyy可表示为: 校正电压的加载方式主要有两种:(a)只在单个电极上施加电压,根据正交信号的相位,判断校正所需keyx的正、负符号,在校正电极A、B中选择一个施加直流电压,调节该电压使正交信号最小化。该加载方式实现简单,但需要手动选择校正电极,在模拟电路中仅适用于开环校正。(b)在两个电极上施加电压,分别为VA、VB,通过调节其平方差使正交信号最小化,一般将二者取为VA=VD+Vq,VB=VD-Vq,有: 式中,VD为预置直流电压,Vq为调节电压。VD一定时,调节Vq既可控制keyx的大小也可改变其正、负符号,因而该加载方式适用于对正交幅值进行闭环控制。 选择加载方式(a)时,假设校正所需的keyx为负,正交响应幅值|yq|与VA的关系为: 选择加载方式(b)时,取VD为固定值,正交响应幅值|yq|与Vq的关系为: 可见,采用加载方式(a)时,|yq|与VA为非线性关系,且在调节VA的过程中,检测模态谐振频率受到直接影响,变化较大。采用加载方式(b)时,若取VD>>Vq,则调节Vq对检测谐振频率的影响可以降至很小,且|yq|与Vq为近似线性关系。若希望正交校正对检测谐振频率的影响最小化,加载方式(b)具备优势。 无论哪种加载方式,使正交响应幅值为零的电压值为所需的正交校正电压,电压小于该值或大于该值时正交响应均不为零,处于欠校正或过校正状态。 加工得到带正交校正结构的双质量硅微陀螺芯片,以陶瓷管壳进行真空封装。安装在PCB电路板上的硅微陀螺表头如图3所示。 图3 硅微陀螺表头及测试电路Fig.3 Vacuum packaged gyroscope on PCB with test circuits 图4 无角速度输入时的驱动速度信号与输出信号Fig.4 Waveform comparison between the drive velocity signal and the zero-rate output one 选择正交误差较大的某硅微陀螺表头进行正交校正实验。无角速度输入条件下,令驱动回路正常工作,表头输出信号与驱动速度信号的波形比较如图4所示,图中上方波形为驱动速度信号,下方波形为输出信号,可见输出信号在相位上滞后驱动速度信号大约90°,主要为正交信号,且结构耦合弹性系数kyx为正。由输出信号幅值结合相关电路参数折算可得该表头的正交误差等效角速度约为354 (°)/s。采用两种校正电压加载方式对该表头进行正交校正,记录输出信号幅值随校正电压的变化情况。同时,由式(15)(16)计算正交响应幅值与校正电压相对变化关系的理论曲线。选择加载方式(a)(b)时,理论曲线与实测数据的比较分别如图5、图6所示。 图5 在单个电极上施加电压时正交信号随VA的变化Fig.5 Relative relationship between quadrature signal and correction voltage when only one electrode is in use 可见,两种电压加载方式下,实测数据的变化趋势与理论曲线基本一致,证明了理论分析的正确性。设计的校正结构参数为:n= 45,d0= 4,p= 2.4。敏感质量mc≈ 0.5 mg,驱动频率为3.8 kHz。由式(9)计算可得,理论上校正354 (°)/s正交误差所需的VA、VB平方差约为119.5 V2。在单个电极上加载时,所需理论校正电压VA约为10.9 V,实测值为12 V,略大于理论值。在两个电极上加载时,若取VD为10 V,则所需理论校正电压Vq约为2.9 V,实测值为3 V,与理论值吻合良好。 实际测试中,调节校正电压使输出信号幅值最小化时,仍然存在100 mV左右的残余信号,将其与驱动速度信号对比可以发现,残余信号为与有用信号同频同相的偏移误差部分,正交信号已被完全消除。 图6 在两个电极上施加电压时正交信号随Vq的变化(VD= 10 V)Fig.6 Relative relationship between quadrature signal and correction voltage when both electrodes are in use(VD= 10 V) 本文设计并分析了硅微陀螺的一种正交误差直流校正方法。对敏感质量的运动分析表明,正交误差主要由结构耦合弹性系数结合驱动运动形成的正交力作用于检测方向引起正交响应产生。合理设计正交校正结构,可实现构建静电耦合弹性系数,并利用敏感质量的驱动运动产生校正静电力,用以平衡正交力。校正力的频率和相位与正交力自然匹配,无需电路控制。校正电压可由结构参数和正交误差等效角速度进行估计。相较于单电极加载方式,校正电压的双电极加载方式适用于对正交幅值进行闭环控制,并且可使校正电压调节对检测谐振频率的影响最小化。实验测试验证了正交信号随校正电压的变化规律,实际校正电压接近理论值,证明了校正结构设计的正确性。该方法在双线振动式硅微陀螺中具备通用性和实用价值。 (References): [1]Shkel A M,Horowitz R,Seshia A A,et al.Dynamics and control of micromachined gyroscopes[C]// Proceedings of the American Control Conference.San Diego,USA,1999:2119-2124. [2]Geiger W,Bartholomeyczik J,Breng U,et al.MEMS IMU for AHRS applications[C]//IEEE/ION Position Location and Navigation Symposium.Monterey,USA,2008:225-231. [3]Lapadatu D,Blixhavn B,Holm R,et al.SAR500 - A high-precision high-stability butterfly gyroscope with north seeking capability[C]// IEEE/ION Position Location and Navigation Symposium.Indian Wells,USA,2010:6-13. [4]YANG Bo,WANG Shou-rong,LI Hong-sheng,et al.The coupling error analysis of the decoupled silicon micro-gyroscope[C]// 5th IEEE International Conference on Nano/Micro Engineered and Molecular Systems.Xiamen,China,2010:356-361. [5]罗兵,张辉,吴美平.硅微陀螺正交误差及其对信号检测的影响[J].中国惯性技术学报,2009,17(5):604-607, 613.LUO Bing,ZHANG Hui,WU Mei-ping.Quadrature signal of microgyroscope and its effect on signal detection [J].Journal of Chinese Inertial Technology,2009,17(5):604-607,613. [6]Saukoski M,Aaltonen L,Halonen K A I.Zero-rate output and quadrature compensation in vibratory MEMS gyroscopes [J].IEEE Sensors Journal,2007,7(12):1639-1652. [7]Sharma A,Zaman M F,Ayazi F.A sub-0.2°/hr bias drift micromechanical silicon gyroscope with automatic CMOS mode-matching[J].IEEE Journal of Solid-State Circuits,2009,44(5):1593-1608. [8]Tatar E,Alper S E,Akin T.Effect of quadrature error on the performance of a fully-decoupled MEMS gyroscope [C]//IEEE 24th International Conference on Micro Electro Mechanical Systems.Cancun,Mexico,2011:569-572. [9]殷勇,王寿荣,王存超,等.一种双质量硅微陀螺仪[J].中国惯性技术学报,2008,16(6):703-706,711.YIN Yong,WANG Shou-rong,WANG Cun-chao,et al.Dual-mass silicon micro-gyroscope[J].Journal of Chinese Inertial Technology,2008,16(6):703-706,711. Design and analysis of a quadrature correction method using DC voltages for silicon micro-gyroscope NI Yun-fang,LI Hong-sheng,YANG Bo,HUANG Li-bin,ZHAO Li-ye,WANG Pan,LIU Jia A quadrature correction method using DC voltages for silicon micro-gyroscope was designed.The quadrature correction was accomplished by a specially designed correction structure in combination with DC voltages.The differential equations of the proof mass’s motion were established in consideration of quadrature error.The causes of the quadrature response and how it affects the drive motion trajectory were then derived.The quadrature correction structure was designed for silicon micro-gyroscope,through which a correction electrostatic force can be generated by using the created electrostatic coupling elastic coefficient and the drive motion.Comparied with traditional quadrature correction methods,this method has the advantage of eliminating the need of frequency and phase control.Two voltage loading methods were designed and analyzed,and the relative relationship between the quadrature response and the correction voltage was verified through experimental test.The actual values of correction voltage are close to the theoretical ones,proving the correctness of the structure design.This method has important application value in linear vibration silicon micro-gyroscope. silicon micro-gyroscope;quadrature error;quadrature correction;DC voltage;structure design TH824+.3 :A 1005-6734(2014)01-0104-05 10.13695/j.cnki.12-1222/o3.2014.01.021 2013-08-06; :2013-11-10 国家自然科学基金项目(61101021);中央高校基本科研业务费专项资金资助(3222003102) 倪云舫(1986—),女,博士研究生,从事MEMS微惯性仪表研究。E-mail:niyunfang@126.com 联 系 人:李宏生(1964—),男,教授,博士生导师。E-mail:hsli@seu.edu.cn
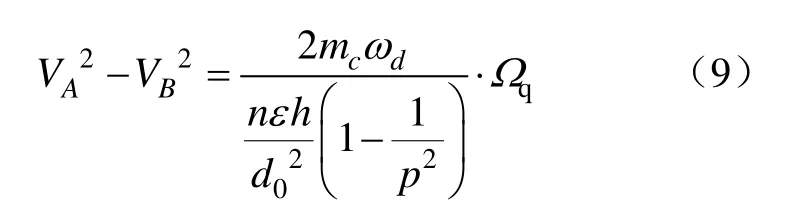
3 校正电压加载方式设计与分析
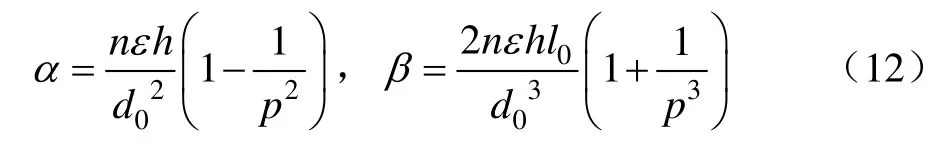

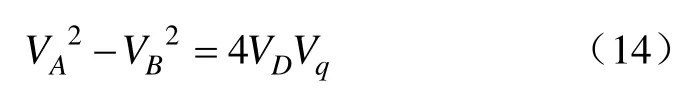


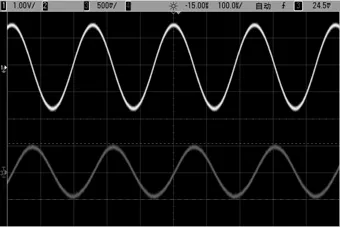
4 实验测试



5 结 论
(Key Laboratory of Micro-Inertial Instrument and Advanced Navigation Technology of Ministry of Education,School of Instrument Science and Engineering,Southeast University,Nanjing 210096,China)
