自适应SA-ACO地磁匹配导航算法

王跃钢，贾 磊，单 斌,2，严 涛

（1.第二炮兵工程大学 自动控制系，西安 710025；2.西北工业大学 自动化学院，西安 710072）

自适应SA-ACO地磁匹配导航算法

王跃钢1，贾 磊1，单 斌1,2，严 涛1

（1.第二炮兵工程大学 自动控制系，西安 710025；2.西北工业大学 自动化学院，西安 710072）

基本蚁群算法的地磁匹配算法易陷入局部最优且算法鲁棒性、稳定性较低，针对这些不足提出一种改进的地磁匹配导航算法。新算法改进了蚁群算法的信息素更新策略并引入参数自适应调整来避免算法陷入局部最优；同时采用带有记忆功能和自适应选择初始温度的模拟退火（SA）算法，无论算法是否陷入局部最优时通过在本次迭代最优路径上强行随机扰动以实现继续寻优。实验结果表明，新算法比传统蚁群优化（ACO）算法有更强的鲁棒性和稳定性。

地磁匹配导航；自适应；模拟退火；蚁群优化；精英策略

地磁匹配导航是利用地球基本物理场之一的地磁场实现导航定位。其原理是当载体通过适配区域时，载体上的磁强计实时测出当地地磁特征值，并将实测特征值序列与载体上预存的地磁基准图进行相关性匹配，估算出载体的实际位置坐标，供给导航计算机解算出导航信息[1-2]。传统的地磁匹配算法有基于相关极值和基于刚性变换两种[3-4]，这两种算法是现在应用最为广泛的地磁匹配算法，但它们都有一定的局限性。基于相关极值的匹配算法往往采用遍历搜索的搜索策略，在基准图上寻找与惯导输出路径形状完全相同且相关性最优的路径，当惯导输出路径的形状与真实路径的形状有偏差时，会造成匹配不可避免的存在偏差，而且在基准图较大的情况下运算量较大，导致算法匹配时间较长，不利于与惯导进行组合。基于刚性变换的匹配算法要求磁传感器没有量测误差，且匹配对象与目标对象已经很接近，当惯导输出的路径误差较大时，匹配结果往往偏差很大。传统的地磁匹配算法的不足要求匹配算法能够自主的寻找路径且有一定的抗噪性。

蚁群算法是一种用来在寻找优化路径的机率型技术，能够执行智能搜索、进行全局优化，具有鲁棒性、正反馈、分布式计算、易于与其它算法相结合等特点。将该算法运用到地磁匹配导航当中可以解决当载体行进路径形状未知且为非直线的条件下自主匹配定位的问题[5]。

蚁群算法求解运算时表现出收敛速度慢、易陷入局部最优的缺点，加之实测的磁场数值往往含有不同程度的噪声，相关函数计算出的相关度量值并不能正确反应真实航迹与匹配航迹的相似程度，这些将导致匹配的路径与真实航迹的偏差较大。本文从蚁群算法自身的改进和引入模拟退火算法两方面着手，提高匹配精度和算法稳定性。

1 基本蚁群优化的地磁匹配算法

蚁群优化是一种用于求解复杂组合优化问题的启发式算法。由于地磁基准图为网格式，因此可将地磁匹配定位看作是多级离散优化问题。设M为蚂蚁的数量，N为测量序列的长度（或称作匹配长度），为载体轨迹上的实测磁场特征值，为基准图上j点处的地磁特征值，为量测序列中对应在基准图上j点的第l个实测值。地磁在初始时刻信息素强度相等，蚂蚁在运动过程中依据路径上信息素强度的大小选择转移路径。地磁匹配导航定位中的测量数据序列往往含有噪声，导致启发式因子对算法造成干扰，在算法搜索过程中蚂蚁始终依据信息素强度来计算状态转移概率，第k级中蚂蚁m由当前所在点i转移到点j的状态概率为如式(1)所示[6-7]：

其中，allowedi表示蚂蚁在点i时可以一步到达的位置，α为信息素启发因子，为i点到j点路径（称为路径(i,j))上的信息素强度，其中点j是点i可一步到达的位置

当每一只蚂蚁完成一次一个步长的搜索后利用度量函数评价该路径的优劣程度，一般采用相似性度量函数，即判断蚂蚁走过的路径上的地磁特征值与实时测量的地磁量测序列之间的相似程度。相似性度量函数有距离度量和相关度量两大类。距离度量算法包括平均绝对差（MAD）算法、平均平方差（MSD）算法、Hausdorff距离算法等。相关度量算法包括积相关（PROD）算法、归一化积相关（NPROD）算法、相位相关（PC）算法等[8]。实际匹配过程中测量序列往往含有不同程度的噪声，导致匹配结果是与含有噪声的地磁序列最相似的路径，而不是真实的路径，这就要求相似性度量函数能够有一定的抗噪性。经过仿真对比发现，在噪声较大的环境下，MAD的抗噪性要优于NPROD，且MAD的匹配时间要远远小于其它算法。所以本文选用MAD作为全局相似性度量函数。全局相似性度量函数和局部相似性度量函数如式(2)(3)所示：

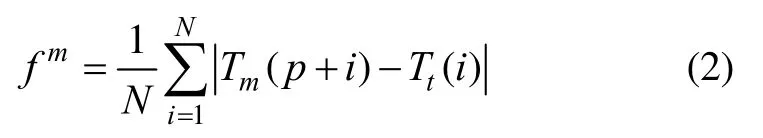
式中，N为匹配长度，为基准图上蚂蚁以p点为起始点第i步所经过路径上的地磁值，为一个匹配步长内的实测地磁强度值序列。

在每只蚂蚁走完一步或者完成对所有N个结点的遍历后，要利用度量函数值对残留信息进行更新处理，在t+1时刻路径(i,j)上的信息素可按如下规则进行调整更新：

式中，ρ为信息挥发系数，1-ρ表示信息残留因子，△τij为本次循环中点i到点j路径上的信息素增量，为本次循环中第m只蚂蚁留在路径上的信息素，num为蚂蚁的总个数，Q为反应信息素更新量的信息素强度因子。信息素更新与相似度评价函数相结合，即蚂蚁走过路径上的地磁特征值与地磁量测序列中的特征值越相似信息素增加的越多，反之则越少。

2 模拟退火自适应蚁群优化的地磁匹配导航算法

虽然基本蚁群算法在解决地磁匹配问题上取得了很好的效果，但该算法仍存在算法稳定性不高、抗噪性不强、易陷入局部最优等缺点。本文从以下蚁群算法自身的改进和融合模拟退火算法两个方面改进算法，以提高匹配的精度和算法稳定性。

2.1 蚁群算法自身的改进

1）信息素更新策略的改进。信息素的正反馈原理是蚁群算法的核心之一，是蚂蚁判断如何选择路径的重要依据，信息素的分布情况直接影响到蚁群的搜索能力[9]。本文采用以下两种方法改进信息素更新策略，以避免算法过早陷入局部最优、提高算法的寻优能力和抗噪性。

一是采用基于精英策略的全局更新与局部更新相结合更新信息素。全局更新中由于整条中的某一段可能是真实路径的一部分，但因为搜索到的这条路径度量值较差，导致本属于真实路径的一部分路径上信息素增加量不大（甚至不增加），下次迭代时蚂蚁选择这段路径的机率明显下降。为此在全局更新的基础上采用改进的局部更新，加强局部路径的相似度判别。与为了适当增强较优蚂蚁释放的信息素的正反馈，以加强较优解在下次循环中对蚂蚁的吸引力而引入精英策略，在每次循环后给全局度量函数值大于本次迭代平均全局度量函数值的路径进行信息素更新，而对小于本次迭代平均全局度量值的路径不进行信息素更新。依据度量函数的变化，在第NC次迭代中信息素的全局和局部两重更新：

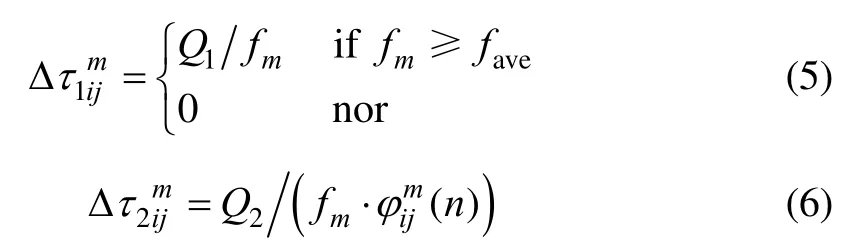
二是设置信息素及信息素增量的上下限以减小路径上信息素的过大差异。蚁群算法陷入局部最优的直接原因就是路径上的信息素差异过大，导致在以后迭代中选择其它路径的概率过小，大量蚂蚁集中在某一相同路径上。将各条路径上的信息素强度限制于区间内，同时在每次更新信息素时将信息素增量限制于区间。当信息素更新使得超出允许范围时可强制地将差异设置在允许的范围内，这样可有效地避免了由算法的正反馈所引起的信息素强度差异过大而陷入局部最优。

综合以上两点，信息素自适应更新的总表达式为

2）参数的自适应调整。蚁群算法在不同阶段需要完成的任务不同，所以不同阶段算法对参数的取值要求也不相同，这就需要算法在不同的阶段自适应调整参数。影响算法随机性的参数主要有信息素启发因子α和信息素挥发因子ρ。信息素启发因子α反应算法中随机因素作用的强度，其值越小搜索的随机性越大；信息素挥发因子ρ反应蚂蚁之间相互影响的强弱，其值越小信息素挥发的越慢，算法的随机性和全局搜索能力越强。当算法求得的单次迭代的最优路径在若干次内没有明显改进时适当减小启发因子α和信息素挥发系数ρ。α和ρ按式(8)和式(9)作自适应调整。

2.2 模拟退火算法与搜索路径

模拟退火算法（SA）的实质是不断地在当前解的邻域中找出一个适合当前解的过程，而适当的邻域能够使算法跳出当前的局部最优解，从而趋于全局最优。模拟退火算法的执行策略为：从一个任意选择的初始解开始探测整个搜索空间，并且通过一个扰动产生一个新解，利用Mertopolis接受准则判断是否接受新解，相应的下降控制温度。以解j代替解i的Mertopolis接受准则如式(3)：

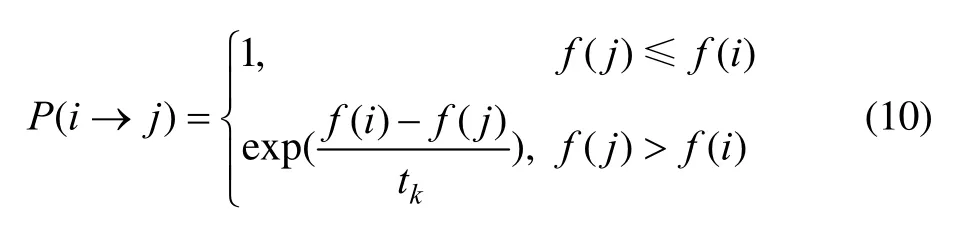
当蚁群算法陷入局部最优，通过算法自身的自适应调整不能够跳出局部最优时，就要通过“外界算法”强行地使蚁群算法跳出，以达到继续寻优的目的。同时，为增强算法的寻优能力，算法未陷入局部最优时也利用模拟退火算法。在蚁群算法本次迭代搜索到的最优路径上随机选取一个结点，通过随机扰动使该结点与最优蚂蚁未选择的一个随机结点交换以产生新路径，比较新路径与该次迭代的最优路径上的度量函数值。若新路径比最优路径的相似度值更优则用新路径替代最优路径，否则采用Mertopolis接受准则决定接受还是放弃[10]。在新路径的基础上继续进行扰动，直至达到终止条件。在退火算法中加入记忆功能[11]，即在接受准则判定是否接受新路径时，不用新路径代替最优路径，以保证最优路径变量存储的永远是度量值最优的路径。

初始温度的设置。退火温度决定算法的性能，因此在进行模拟退火时，先计算该次迭代中蚂蚁走过所有路径的度量函数值fm，判断是否有度量函数值小于fmax的，若有则初始温度，若没有则初始温度。

退火方案。温度下降过快会导致算法产生淬火现象，使搜索不完全。这里采用指数降温方案，即，其中0.95＜μ＜1，本文取μ=0.97。

终止条件。为了简化计算，当温度降到某一预先设定值时算法便停止计算。

2.3 算法实现步骤与流程

以下给出模拟退火自适应蚁群优化的地磁匹配导航算法的具体步骤：

2）将num只蚂蚁放到起始点上，每只蚂蚁按式(1)选择路径，选择路径并进行一步转移后按式(3)计算局部度量函数值，通过迭代完成一个匹配步长的搜索；

3）将每只蚂蚁走过的路径按式(2)计算全局度量函数值fm，并计算全局度量函数平均值fave及全局度量函数最优值fbest；

4）判断算法是否陷入局部最优，若是则转到步骤5)，若不是则转入步骤6)；

5）按式(8)(9)进行参数的自适应调整；

6）按模拟退火算法的初始温度设置方案设置初始温度；

依据 AAS-1996 结果的进一步分析，3 种不同的不安全型依恋模式对 PTSD 的影响也存在差异：回避型依恋模式的个体 PTSD 的发生率最低，仅有14.3%（1/7）；焦虑型依恋模式的个体 PTSD 发生率其次，为 46.4%（13/28）；而恐惧型依恋模式的个体 PTSD 发病率最高，达到 66.7%（8/12），3 种不同的不安全型依恋模式个体的 PTSD 发生率差异有统计学意义（χ2＝13.859，P＜0.01），表明恐惧型依恋模式的失独个体更容易患 PTSD。

7）在此次迭代的最优路径上随机选取一个结点，将该结点与最优蚂蚁可以选择但未走过的一个随机结点交换，并按式(1)完成一个匹配步长的搜索，计算扰动后的路径度量函数值f′；

9）判断是否达到退火终止条件，若未达到则采用退火方案进行降温并转到步骤7)，若达到终止条件则将算法本次迭代最终得到的最优路径作为本次迭代的最优路径；

10）按式(5)~(7)更新信息素并限制信息素及信息素增量的上下限，判断是否达到最大迭代次数，若未达到则转到步骤2)，若达到最大迭代次数转到步骤(11)；

3 仿真试验与分析

假设匹配的起始点已知，且载体每一步运动只能够移动到当前点周围的四个邻域点。仿真时试验的地磁基准图采用某地区实测高精度X分量基准图，地磁基准图180×180个网格的地磁图，网格大小为15.3 m ×9.9 m。设载体从起始点A点沿预定路径运动到终点B点，实测地磁强度值序列tT由真实路径上的地磁基准值和噪声相叠加构成，其中噪声为均值为 0，标准差为10、20、30的高斯分布白噪声。将300只蚂蚁放在起始点A点上，设置如下参数：匹配步长N=10，蚁群算法最大迭代次数，，模拟退火的迭代次数为 20次，按照算法的流程开始运行。如图 1至图 3为仿真结果对比图，为了便于观察匹配结果，将匹配结果图显示范围缩小为原地磁图的一部分。

图1至图3为噪声标准差为30 nT的高斯白噪声环境下三种算法的一次匹配结果。采用模拟退火蚁群优化的地磁匹配算法在稳定性和抗噪性方面均有很大程度地提高。如表1所示，三种算法分别在标准差为10 nT、20 nT、30 nT高斯分布白噪声情况下各仿真100次。由仿真结果可以看出，基本蚁群算法与改进的蚁群优化算法在完全匹配概率和导航定位精度方面几乎相同，其完全匹配概率最优为27%和28%，终点导航定位偏差的标准差最小为83.64 m和78.29 m。而自适应模拟退火优化的地磁匹配导航算法完全匹配概率和终点导航定位偏差标准差最小能达到94%和22.74 m。

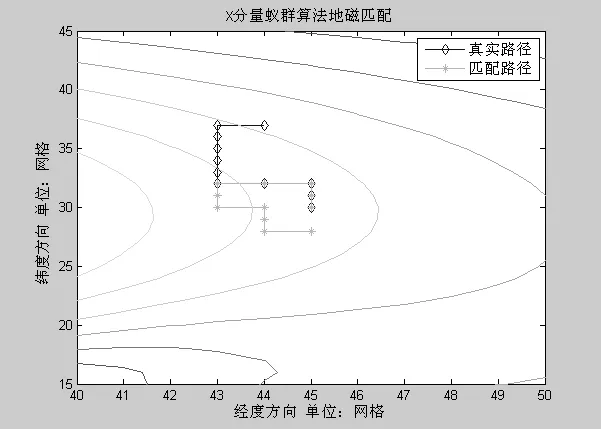
图1 基本蚁群算法的匹配结果Fig.1 Matching result of the basic ant colony algorithm

图2 改进蚁群优化的匹配结果Fig.2 Matching result of improved ant colony e-optimization

图3 模拟退火蚁群优化的匹配结果Fig.3 Matching result of simulated algorithm annealing ant colony optimization

表1 不同算法匹配精度比较Tab.1 Matching precision of different algorithms

4 结 论

本文研究了自由任意路径的地磁匹配导航算法，在基本蚁群算法的基础上，提出了基于自适应模拟退火蚁群优化的地磁匹配导航算法，从蚁群算法自身的改进和加入模拟退火算法强行继续寻优两个方面改进匹配算法。在蚁群算法自身改进方面，改进了信息素更新规则，并采用算法参数的自适应调整；在模拟退火算法中加入记忆功能和依据蚁群算法寻优结果自适应选择初始温度。实验结果表明，基于模拟退火蚁群优化的地磁匹配导航算法能够防止蚁群算法陷入局部最优，较大程度地增强了算法的寻优能力以及算法的抗噪性和稳定性。

（References）：

[1]Guo Caifa,Li Anliang,Cai Hong,et al.Algorithm for geomagnetic navigation and its validity evaluation[C]//IEEE International Conference on Computer Science and Automation Engineering.Shanghai,2011:573-577.

[2]单斌，王跃钢，杨波.地磁多特征量匹配定位关键技术研究[C]//第二届信息、电子与计算机工程国际学术会议.2010，11：721-725.SHAN Bin,WANG Yue-gang,YANG Bo.Study on key technologies of multi geomagnetic elements matching localization[C]//Proceedings of The 2010 International Conference on Information Electronic and Computer Science.2010,11:721-725.

[3]Zhao Jianhu.Study on underwater navigation system based on geomagnetic match technique[C]//The Ninth International Conference on Electronic Measurement ＆Instruments.Beijing,China,2009.

[4]Kato N,Shigetomi T.Underwater navigation for longrange autonomous underwater vehicles using geomagnetic and bathymetric information[J].Advanced Robotics，2009,23(7):787-803.

[5]陈励华，王仕成，乔玉坤.基于蚁群优化的地磁场匹配改进算法[J].电光与控制，2010，17(8)：49-52.CHEN Li-hua,WANG Shi-cheng,QIAO yu-kun.An improved magnetic field contour matching algorithm based on ant colony optimization[J].Electronics Optics and Control,2010,17(8):49-52.

[6]Fuellerer G,Doerner K F,Richard F,et al.Ant colony optimization for the two-dimensional loading vehicle routing problem[J].Computers and Operations Research,2009,36(3):655-673.

[7]Zhu Jingwei,Rui Ting,Jiang Xinsheng,Juelong Li.Ant colony algorithm based on simulated annealing method[C]//2010 International Conference on Circuit and Signal Processing.2010-12:290-293.

[8]陈卫兵.几种图像相似性度量的匹配性能比较[J].计算机应用，2010，30(1)：98-101.CHEN Wei-bing.Comparison of matching capabilities in similarity measurements[J].Journal of Computer Applications,2010,30(1):98-101.

[9]郑卫国，田其冲，张磊.基于信息素强度的改进蚁群算法[J].计算机仿真，2010，27(7)：191-194.ZHENG Wei-guo,TIAN Qi-chong,ZHANG Lei.An improved ant colony algorithm based on pheromone intensity[J].Computer Simulation,2010,27(7):191-194.

[10]ZHU Jing-wei,RUI Ting,LIAO Ming,ZHANG Jin-lin.Multi-group ant colony algorithm based on simulated annealing method[J].Journal of Shanghai University (English Edition),2010,14(6):464-468.

[11]ZHU Zhan-long,YANG Gong-liu,SHAN You-dong,et al.Comprehensive evolution method of geomagnetic map suitability analysis[J].Journal of Chinese Inertial Technology,2013,21(3):375-380.

Adaptive SA-ACO geomagnetic matching navigation algorithm

WANG Yue-gang1,JIA Lei1,SHAN Bin1,2,YAN Tao1
(1.Department of Automation,The Second Artillery Engineering University,Xi’an 710025,China;2.School of Automation,Northwestern Polytechnical University,Xi’an 710072,China)

In view that the geomagnetic matching algorithm based on the basic ant colony algorithm tends to fall in local optimum and the robust and stability of the basic algorithm are low,an improved geomagnetic matching navigation algorithm is proposed.To avoid the algorithm fall in the local optimum,the strategy of pheromone updating is improved and the adaptive adjustment of parameters are introduced.Meanwhile,the simulated annealing algorithm with memory function and adaptive determination of initial temperature is also introduced.So whether the algorithm fall in local optimum or not,it could continue to search better route by applying random disturbances on the best route of this iteration to achieve continued optimization.The experiment results show that the new algorithm is more robust and stability than traditional ant colony optimization.

geomagnetic matching navigation;adaptive;simulated annealing;ant colony optimization;elitist strategy

V249.32

：A

1005-6734(2014)01-0089-05

10.13695/j.cnki.12-1222/o3.2014.01.018

2013-10-14；

：2013-12-09

国防预研（103030203）

王跃钢（1958—），男，教授，博士生导师，从事导航与制导技术研究。E-mail：wangyueg@163.com