波浪动力艇模型自航试验及数值仿真

李聪，王冬姣，叶家玮，李德玉，梁富琳

华南理工大学土木与交通学院，广东广州510641

波浪动力艇模型自航试验及数值仿真

李聪，王冬姣，叶家玮，李德玉，梁富琳

华南理工大学土木与交通学院，广东广州510641

为解决受控主动摆翼驱动装置复杂、机械效率较低的问题，研究依靠升沉运动产生的力矩来驱动俯仰运动的被动摆翼装置，并将其应用于波浪动力艇。在波浪作用下，将被动摆翼安装于艇体底部的一定位置处，产生的推力即可推艇前进。在模型试验中，通过改变波浪周期、波高和控制机构的设置，比较试验艇的自由航行速度。结果表明，试验艇的航速与波高呈正相关关系，且当波长与船长之比约为1.8时推进效果最佳。通过数值仿真，显示两种控制机构配置时的水翼工作过程，并估算在一定波浪参数下波浪动力艇可达到的航速，所估算的航速与试验结果吻合较好。

被动式摆翼；波浪推进；模型试验；数值仿真

0 引 言

由波浪引起的摇荡运动是船舶在海上航行时阻力增加的主要原因。在船舶设计中，通常采取为主机增加储备功率的措施来克服由波浪引起的阻力增值，同时设置舭龙骨或减摇鳍这类专用附体以降低摇摆幅度。尽管采用附体的方法比较直接，但会进一步增加阻力，而引入减摇鳍等主动控制机构，又会增加额外能耗。

人类在研究海洋哺乳类动物的过程中，发现长途迁徙的海洋哺乳类动物经过长期进化已掌握了利用波浪能辅助前进的技巧。例如，鲸可以在一定的海况下从波浪中获取前进所需的约30%的能量［1］。而捕鲸时，死鲸有可能会被波浪推动而远离捕鲸船，从而为捕鲸者带来麻烦［2］。在这种情况下，鲸鳍并不能从死鲸处获得驱动能量，但在鲸体摇荡运动和波浪质点速度的驱动下，仍可产生推力。在以上过程中，鳍是以沉浮和俯仰相耦合的摆动方式在工作。事实上，鱼尾式摆动推进被认为是最高效的推进方式［3］，这也为波浪能在船舶推进上的应用提供了强有力的支撑，并受到关注。在摆动水翼的推力产生机理方面，已有一些试验研究。例如，改变升沉、俯仰幅度和其间的相位差以及水翼前进速度，测量水平、竖直作用力和俯仰力矩、推进效率的实验［4］，该研究认为，水翼的俯仰在相位上超前升沉90°时推进效率最佳，但值得注意的是，相位差的符号取决于所定义的参照系。另外，在不同斯特劳哈尔数和相位差下的涡流场显示试验中发现，当水翼后缘涡排列为逆卡门涡街时，会产生推力［5］。为了说明摆翼推进装置的有效性，Yamaguchi和 Bose［6］利用前人发表的摆翼设计图谱，对一艘载重量为20万吨的油轮进行了对比性推进器设计。结果显示，后半弦长为柔性的水翼的推进效率比最佳MAU5-55螺旋桨高3.5%，且受航速的影响较小，但如何为摆翼设计合适的驱动机构是问题的关键。相对常规推进器所需的转轴，由于驱动水翼以一定的相位差进行沉浮和俯仰运动的机构更为复杂，因此主动受控摆翼在总的推进系数上不一定占有优势。

综上所述，基于对一种既能减摇又对推进有利的新型附体的需求、被动式摆动水翼在波浪能获取上的可行性和相对高效性，以及主动式驱动机构不可避免的效率损失，认为可以开发一种通过被动摆翼利用波浪能推进且适合远程无人海洋观测的小艇。由于直接使用波浪能作为动力来源，不需要布置燃油舱，因而波浪动力艇可以提供比常规动力艇更为充裕的实用舱容。在本文设计的摆翼推进装置中，水翼的俯仰由其本身升沉运动所产生的力矩驱动；一列水翼被水平布置于船基线以下，并在竖直面内设置由复位弹簧、限位绳和摆杆组成的平面运动机构，以控制水翼的俯仰运动。这些水翼可为船的摇荡运动增加阻尼，同时，通过自动调节相对水流的攻角，还可持续将所吸收的波浪能转化为推力。

1 理论依据

1.1 被动式摆翼原理

与主动式摆翼按预定的升沉幅度、俯仰角和相位差运行不同，被动式摆翼的升沉运动取决于船在波浪中的运动响应及其安装位置，而俯仰角和相位差则与水翼处的来流速率、倾角有关。被动摆翼的工作原理如图1所示。

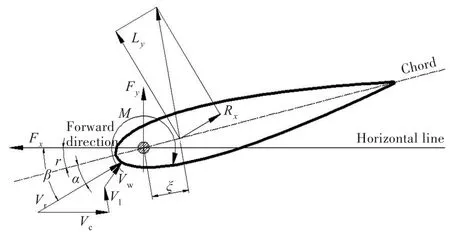
图1 翼剖面上的水流和力Fig.1 Flow and forces on the foil section

图中，Vr为转轴处的来流速度矢量，其与水平线的夹角为 β。Ly和Rx分别为水翼在Vr作用下产生的升力和阻力。通过把Ly和Rx向水平和竖直方向分解叠加，得到与船前进方向相同的推力Fx和抵抗船摇荡运动的竖直力Fy（图中矢量大小未按比例画出）。只要转轴位于水翼水动力中心之前，来流就能以ξ为力臂推动水翼作俯仰运动，以达到一定的俯仰角r，从而获得合适的攻角α，并产生持续的推力。图1中俯仰角r的方向定义为正。回复力矩M与水翼相对船体的俯仰角和控制机构的刚度有关，通过改变回复力矩，即可控制水翼的俯仰幅度，从而影响系统的推进效率。

1.2 转轴处来流的速度构成

由于水翼的弦长远小于波长和船长，故认为作用于整个水翼上的来流速度和偏角等于转轴处的值是一个合理的近似。Vr的构成可由下式表达（图1）：

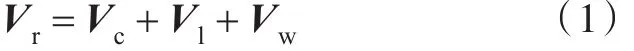
式中：Vc为由船前进引起的来流速度；Vl为由转轴摇荡引起的水流速度；Vw表示转轴处的波浪质点速度。

1.3 转轴摇荡速度Vl

船在任意方向波浪的作用下，将作六自由度的摇荡运动。作为初步研究，将只考虑迎浪状态，此时，船的运动主要为纵摇和垂荡。Vl的计算方法如图2所示。

在任意时刻，转轴相对重心G的水平坐标xl(t)和竖直坐标zl(t)均可由安装位置和船体运动位移的时程算出。定义矢量R(t)的方向由G指向转轴，故有

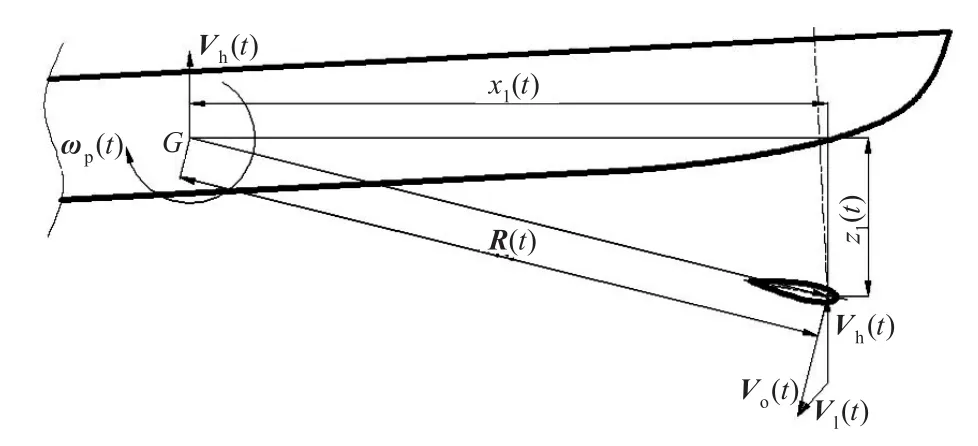
图2 转轴摇荡速度计算Fig.2 Calculation of pivot motion velocity

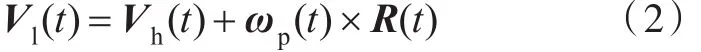
式中：Vh(t)为船体垂荡速度；ωp(t)为船体纵摇角速度。对于水翼，相应的水流速度Vl与图中所示的矢量大小相等，方向相反。

1.4 波浪质点速度Vw

为便于分析结果，试验在规则波中进行。考虑到波浪参数、实验水深和各种波浪理论的适用范围，Vw的计算采用有限水深微幅波理论。Vw的两个分量的计算公式如下［7］：

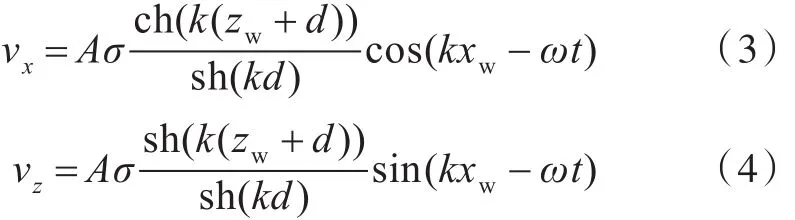
式中：vx和vz分别为Vw的水平和竖直分量；A为波幅；σ为波浪圆频率；k为波数；t为时间；d为水深；xw和zw定义如下：

式中：θ为浪向角，船迎浪时θ=180°；x和 z分别为t时刻水翼转轴中点（y=0）在固定参照系（FRA）中的纵向和竖直坐标。FRA的原点设置在静水面上，且与船重心G的纵向初始位置处于同一竖直线上，x轴指向船的前进方向，z轴竖直向上。

2 模型试验

2.1 试验模型

在试验模型的甲板以上设有焊接成型的框架，用于连接两个片体，并安装有水翼控制机构（图3）。船体由玻璃钢制成，试验时，压载至轻微尾倾。根据被动水翼的工作特点，选择厚度比为0.18的对称翼型，使其在上、下升沉时具有相同的性能，并且在不同的攻角下均有较大的升阻比。为便于调整，试验中，采用外置平面运动机构控制水翼的运动，而在实际应用中将使用集成于竖杆内的程控变刚度扭转弹簧和橡胶限位器，以消除外置控制机构带来的阻力增加。船体及水翼的各项参数如表1所示。

图3 试验模型照片Fig.3 Photo of the test model

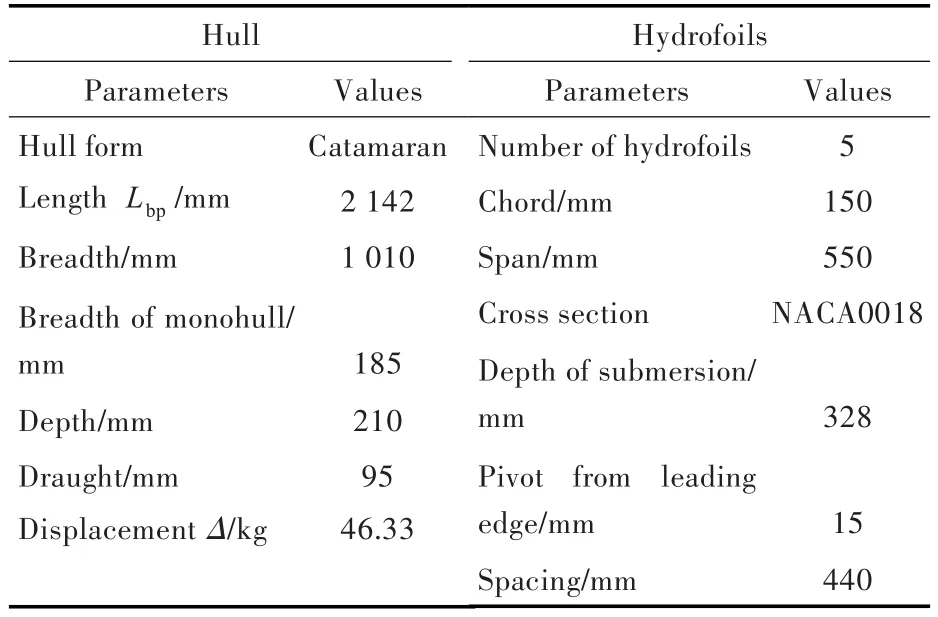
表1 模型参数Tab.1 Parameters of the test model

采用双体方案是为了在船体较小时安装展长较大的摆翼，同时，各片体较小的宽度和方形系数也有利于减小高海况下的阻力增值。此外，双体结构还能提供比单体结构更大的甲板面积，可以布置其它动力能源装置，如大面积太阳能板，这对于不携带燃油发电机的波浪动力艇来说比较有利。

2.2 试验参数选取

根据水翼控制机构的设置，试验分测速组与对照组。测速组所用的波浪参数如表2所示，对照组只针对部分参数进行。记录每组波浪参数下试验艇通过一定距离所用的时间，得出其自由航行速度。

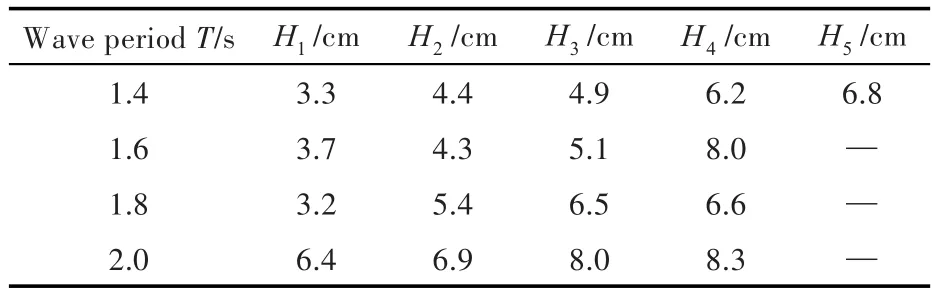
表2 波浪参数Tab.2 Parameters of generated wave

测速组中，水翼可随来流转动，相对船体的最大转角限制为28°，该组的结果将在下节分析。在对照组中，水翼相对船体固定，水翼的沉浮和俯仰运动完全由船体的运动决定，测得的航速明显较低，其中的原因将在数值仿真部分讨论。

2.3 航速与波高和周期的关系

测速组的试验结果按波浪周期分组。图4以波高为横坐标，航速为纵坐标对数据进行了表达。

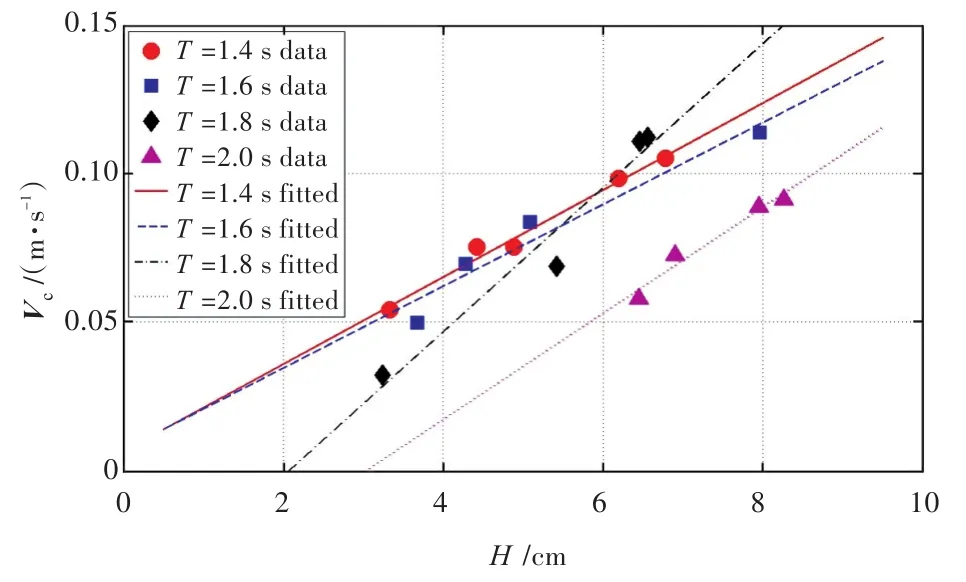
图4 各波浪周期下航速与波高的关系Fig.4 The variation of ship speed with respect to wave height in wave period

在各波浪周期下，航速与波高之间存在近似的线性关系，可对数据进行线性拟合。由图4可见，当波浪周期T=1.4 s时，航速的线性程度比T=1.6 s时高，但从统计上看，该周期区间内的航速差别不大。在T=1.8 s附近，航速对波高的变化最为敏感。当T=1.8 s时，在5 cm以下的波高中，模型的航速较慢，但当波高超过6 cm后，航速即可超过周期较短时的值。然而，若波浪周期继续增大，航速便会显著下降。

图4仅对试验数据进行了简单陈述。为深入分析试验结果，利用拟合结果将航速（单位m/s）与波浪周期和波高的关系绘制成如图5所示的等值线图。

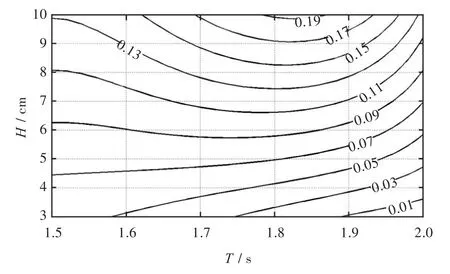
图5 航速的等值线图Fig.5 Contours of forward speed

由于每个波浪周期对应的航速均随波高线性增加，因此在图5中，同一横坐标上的等值线是均匀分布的。当 T=1.8～1.85 s时，等值线分布最为密集，故这个区域的航速随波高增加最快，其对应的波长约为船长Lbp的1.8倍。波长由数值求解色散方程得到，并考虑水深的影响。当试验艇工作在10 cm波高环境下时，只有当波浪周期接近最佳周期时，航速才能达到0.19 m/s。

当模型工作在T＜1.6 s，H＜6 cm的波浪中时，相应区域中的等值线趋于水平，这说明航速对周期的变化并不敏感。当T＞1.95 s，即波长大于2倍的 Lbp，波高低于3.5 cm时，航速极慢，且从单位波高增量中获得的航速增值也小（图5右侧）。在长波中，船相对于水的摇荡运动比中等波长中的小，故需要更大的波高以获得相同的航速。这说明被动式摆翼主要依靠与水的竖直往复相互作用来产生推力。

3 数值仿真

3.1 程序简介

为深入探讨波浪推进的工作特性，本文基于准定常水翼理论编制了仿真程序，可对一个摇荡周期内的推力产生过程进行仿真。船体运动和波浪中的阻力增值采用三维势流理论计算，并考虑水翼与船体的相互作用。首先计算得到时均推力随假设航速变化的曲线，并与波浪中的阻力曲线相交，估算可达到的航速，然后对比实测航速检查方法的正确性。随后，将结合试验现象介绍一些有意义的结果。

3.2 程序正确性检验

仿真程序中的波浪参数选为周期T=1.6 s，波高 H=7.96 cm。阻力曲线与推力曲线相交的情况如图6所示，图中横坐标Vc表示航速，纵坐标Rt和Fx分别表示阻力和推力。

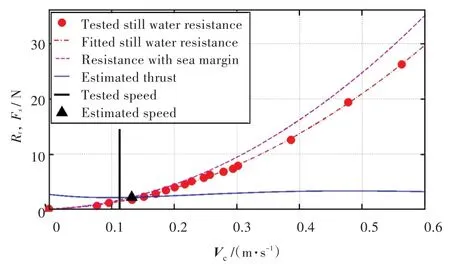
图6 阻力与推力的关系Fig.6 Relationship between resistance and thrust

图中的圆点为静水阻力试验结果。通过这些圆点的点划线为二次拟合曲线，从中可知阻力与航速的平方成正比。以模型漂力的计算值为波浪中阻力增值，绘制波浪中的阻力曲线如图中虚线所示。图中实线代表时均推力计算结果，三角形标记对应波浪中阻力与推力曲线的交点，估算出的航速为0.132 m/s，稍大于粗实线标出的实测航速 0.114 m/s。

3.3 典型水翼轨迹

图7给出了船重心前方水翼的典型展开运动轨迹，用以说明一个周期内摆翼的工作状态。

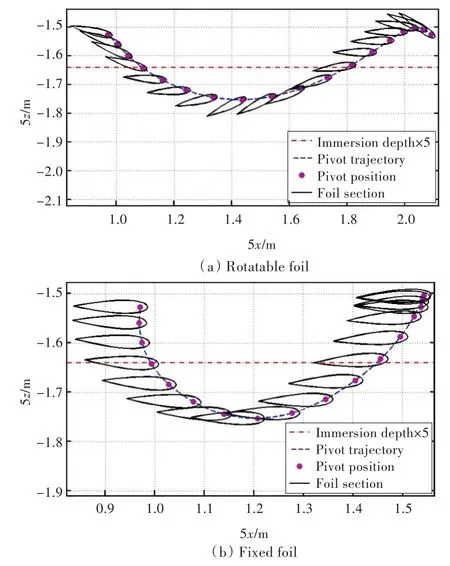
图7 典型水翼展开轨迹Fig.7 Typical stretched foil trajectory

水翼在一个摆动周期内前进的距离不足两倍弦长，为避免水翼剖面过度重叠，同时保持轨迹形状不变，将转轴轨迹在水平和竖直方向均拉伸5倍绘制。转轴坐标定义在FRA中。水翼的形状尺寸及俯仰角度均按实际绘出，相邻翼剖面之间的时间间隔为0.1 s。图中水平贯穿的点划线代表水翼的平衡浸深。

从图7可以发现被动水翼工作过程中的两个性质：

首先，是转轴轨迹。由于水翼安装在船上，转轴的沉浮速度是船体摇荡速度在安装位置的竖直分量，故船体纵摇对水翼升沉的影响随着水翼与船重心间水平距离的增加而增加。假设船的前进速度恒定，但当其与转轴处船体纵摇圆周速度的水平分量叠加后，转轴前进的速度也不再是常量。最终，在所有速度分量的耦合作用下，形成了关于平衡位置不对称的转轴轨迹。

其次，是水翼俯仰方式。以往对主动式摆翼的试验和数值计算均指出，当升沉相位超前俯仰90°时，推进效率最高［8-11］，即当转轴以最大升沉速度通过平衡位置时，水翼的俯仰角达到最大。在测速组试验中，水翼可由来流驱动，来流垂向分速度越大，俯仰角便越大。船艏艉处水翼的升沉运动主要由船体纵摇引起。当船体纵摇角速度最大，即重心处于波峰或波谷时，水翼的偏转最大，这与试验现象是相符的。而在对照组试验中，水翼相对船体固定，俯仰角不由来流决定。各水翼的俯仰幅度与船体的纵摇幅度相等，仅为3.57°，当来流倾角较大时，处于失速状态，不能有效产生推力。在 T=1.8 s，H=6.6 cm波浪的作用下，对照组的航速仅为0.067 m/s，比水翼可转动时降低了40%。可见，以较大俯仰角捕捉最大的来流垂向分速度是一种高效的推力产生方式。此外，由于所处位置和时刻的波浪质点速度不同，水翼从不同方向通过同一深度时的俯仰角也不对称。

3.4 水翼受力

为了显示不同时刻水翼上水动力的大小和方向，绘制了与图7（a）中可转动水翼轨迹相对应的力矢量图，如图8所示。

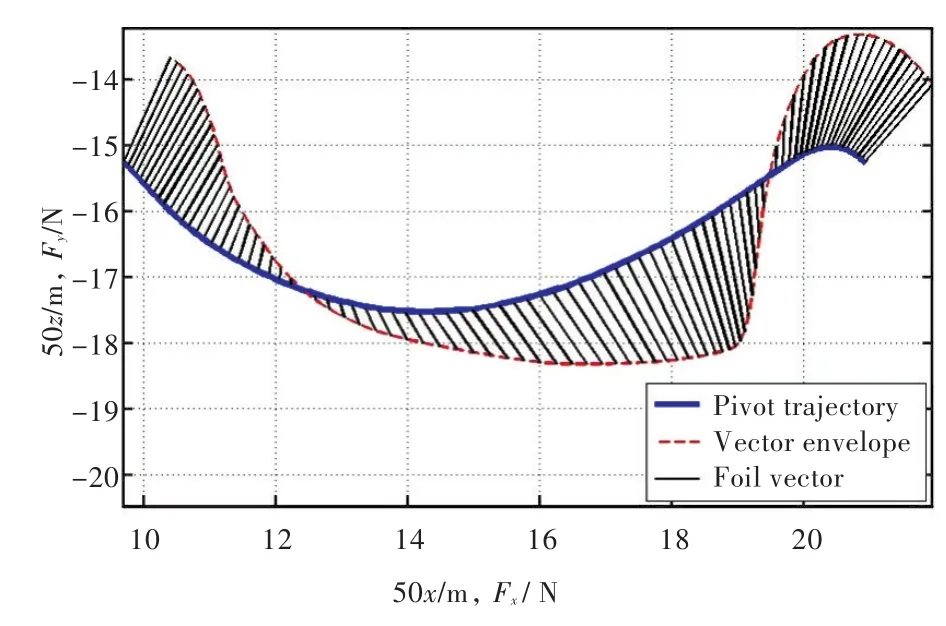
图8 水翼上的力矢量Fig.8 Force vectors on foil

图8中的转轴轨迹绘制原理与图7相同，但为了使同一数轴上直接读出的力单位为牛顿，两个方向上的拉伸倍数均设为50。力的方向由转轴轨迹指向矢量包络线，相邻矢量间的时间间隔为0.02 s。只需将矢量向相应的坐标轴投影，并读出端点间的距离，即可获得推力与竖直力的大小。

由图8可见，水翼上力的主要分量趋向于抵抗船的摇荡运动。较大的推力分量出现在水翼俯仰角较大时，若大的俯仰角不能与较大的竖直来流速度同步，时均推力便会减小。另外，水翼在平衡位置附近产生的推力也较小。

4 结 语

本文为在海上利用波浪能进行低速推进提供了一个可行的方案。试验中，试验艇总能前进的事实证明本文所采用的波浪能推进方案是行之有效的。在测速组中，航速总是随波高成比例增加，但增量对波高的敏感度取决于波浪周期。当波高H＜6 cm时，较短波长中的航速高于长波中的航速。当 H＞6 cm时，在波长约为1.8倍船长处出现了一个最佳响应区，试验艇可从较小波高中获得较高的航速。若波长大于2倍船长，则推进性能下降。数值仿真得出了基本正确的航速估计。被动式摆翼的转轴运动轨迹由船的摇荡运动和航速决定，与水翼的安装位置也有关系，其关于平衡位置呈不对称形状。当水翼的俯仰角极值与最大来流竖直分速度同步时，可产生较强的推力。在水翼的一个运行周期内，推力主要在转轴远离平衡位置时产生。

［1］BOSE N，LIEN J.Energy absorption from ocean waves：a free ride for cetaceans［C］//Proceedings of the Royal Society of London.London， Great Britain，1990：591-605.

［2］樊世荣.利用海浪动力推动船只前进［J］.海洋技术，1982（4）：31-45.FAN Shirong.Utiliation of wave energy for ship propulsion［J］.Ocean Technology，1982（4）：31-45.

［3］张晓庆，王志东，张振山.二维摆动水翼仿生推进水动力性能研究［J］.水动力学研究与进展：A辑，2006，21（5）：632-639.

ZHANG Xiaoqing，WANG Zhidong，ZHANG Zhenshan.Hydrodynamic study of bionic propulsion for 2-D flapping foil［J］.Journal of Hydrodynamics（Ser.A），2006，21（5）：632-639.

［4］READ D A，HOVER F S，TRIANTAFYLLOU M S.Forces on oscillating foils for propulsion and maneuvering［J］.Journal of Fluids and Structures，2003，17（1）：163-183.

［5］王肇，宋红军，尹协振.二维翼型非定常运动的涡流场显示——2俯仰运动和沉浮/俯仰联合运动［J］.流体力学实验与测量，2004，18（4）：38-42.

WANG Zhao，SONG Hongjun，YIN Xiezhen.The visualization of vortex field of unsteady motion for 2-D airfoil—2 pitching motion and heaving/pitching composite motion［J］.Experiments and Measurements in Fluid Mechanics，2004，18（4）：38-42.

［6］YAMAGUCHI H，BOSE N.Oscillating foils for marine propulsion［C］//Proceedings of the Fourth（1994）International Offshore and Polar Engineering Conference.Colorado，USA，1994：539-544.

［7］夏国泽，马乾初.船舶流体力学［M］.武汉：华中科技大学出版社，2003.

［8］杨亮，苏玉民，秦再白.粘性流场中二维摆动水翼的水动力分析［C］//第七届全国水动力学学术会议暨第十九届全国水动力学研讨会文集（下册）.北京，2005：830-838.

［9］BELIBASSAKIS K A，POLITIS G K.Hydrodynamic performance of f l apping wings for augmenting ship propulsion in waves［J］.Ocean Engineering，2013，72：227-240.

［10］王亮，王明，吴锤结.自主推进俯仰震荡翼型的数值模拟研究［J］.固体力学学报，2006，27（增刊）：110-114.

WANG Liang，WANG Ming，WU Chuijie.Numerical simulation of self-propelled oscillating foil［J］.Acta Mechanica Solida Sinica，2006，27（Supp）：110-114.

［11］王志东，丛文超，张淋，等.自主航行模式下二维摆动尾鳍的推进性能研究［J］.江苏科技大学学报（自然科学版），2010，24（6）：523-528.

WANG Zhidong，CONG Wenchao，ZHANG Lin，et al.Propulsion performance of 2D oscillating caudal fin under the autonomous navigation mode［J］.Journal of Jiangsu University of Science and Technology（Natural Science Edition），2010，24（6）：523-528.

Free Running Model Tests and Numerical Simulation on a Wave Propelled Craft

LI Cong，WANG Dongjiao，YE Jiawei，LI Deyu，LIANG Fulin

School of Civil Engineering and Transportation，South China University of Technology，Guangzhou 510641，China

To deal with the complexity and inefficiency of the driving device for actively controlled oscillating foils，the concept of passive oscillating foils，whose pitch motion is driven by the moment induced by the heave motion，is investigated and applied to a wave propelled craft.Particularly，the foils are installed beneath the craft to generate thrust so that the craft can move forward.In the following model test，free running speeds under different wave period，wave height，and foil control configurations are measured and then compared.It is shown that the free running speed of the craft is of positive correlation with wave heights，and the optimum performance is obtained when the ratio of incident wave length to ship length is approximately 1.8.Through numerical simulation，the working process of foils with two different control mechanism configurations is also demonstrated，where the free running speed under certain wave parameters is predicted，and the result is in good agreement with the measured data.

passive oscillating foil；wave propulsion；model test；numerical simulation

10.3969/j.issn.1673-3185.2014.02.002

http://www.cnki.net/kcms/doi/10.3969/j.issn.1673-3185.2014.02.002.html

U661.73

A

1673－3185（2014）02－06－06

期刊网址：www.ship-research.com

2013－10－15 网络出版时间：2014-3-31 16:32

教育部博士点基金资助项目（20090172110008）

李聪（1988－），男，硕士生。研究方向：船艇研究与设计。E-mail：tonylee7335＠qq.com

王冬姣（1963－），女，博士，副教授。研究方向：船舶与海洋工程水动力学。E-mail：djwang＠scut.edu.cn

王冬姣

［责任编辑：卢圣芳］