基于螺旋桨负荷特性的双桨船操纵性预报
2014-07-19胡晓芳陈松林
胡晓芳,陈松林
1中国舰船研究设计中心,湖北武汉430064 2海军装备部,北京100841
基于螺旋桨负荷特性的双桨船操纵性预报
胡晓芳1,陈松林2
1中国舰船研究设计中心,湖北武汉430064 2海军装备部,北京100841
通过对双桨船内、外两桨负荷变化情况及其对舰船回转性和回转速降计算结果影响的分析,提出了采用等功率法分别计算双桨船内、外两桨的转速、进速系数等,进而确定两桨的推力和转艏力矩,从而进行双桨船回转性和回转时速降预报。以某双桨船为例,分别用等转速法、等推力法和等功率法进行回转轨迹、回转时螺旋桨推力、速降和转艏力矩的计算。计算结果表明:采用等功率法与采用等转速法所得到的回转轨迹基本相同,较之等推力法所得到的回转直径的计算结果更接近实船实际情况;采用等功率法所得到的速降介于等转速法和等推力法之间,最为接近实船的实际情况。
操纵性;MMG数学模型;双桨船;螺旋桨;负荷
0 引 言
在设计阶段对船舶操纵性进行计算预报是对每一型新造舰船的基本要求,一般采用MMG分离型操纵性数学模型进行计算,根据所确定的各项水动力导数模拟舰船在规定状态下的运动得到。在操纵性计算预报中,对于螺旋桨推力的处理以前多采用等转速法或等推力法,但实际上,由于回转过程中螺旋桨的负荷发生了变化,实际所产生的推力与按照这2种计算方法所得到的结果均有差异,特别对于双桨船,由于回转过程中两桨处的来流速度不同,负荷变化尤为明显。对此,国内外的学者也开展了研究,如 Abramowski[1]提出了一种利用人工神经网络的方法来预报船舶操纵工况下螺旋桨推力的方法。邓爱民等[2]利用实船测试得到的两桨转速计算两桨的推力,并计算出因两桨推力不同所引起的转向力矩。王化明等[3]利用船舶回转过程中两桨处不同的伴流分数计算两桨的推力,进而计算两桨推力不同所引起的转向力矩。本文将在前人研究的基础上,通过分析螺旋桨负荷产生变化的原因及内、外桨负荷变化对舰船回转性产生的影响,提出采用等功率法计算舰船内、外两桨推力的方法;并以某双桨船为例,将典型操舵角下的操纵性计算预报结果,与利用等转速法和等推力法所得到的回转轨迹及速降等参数的预报结果,以及实船的测试结果进行对比分析。
1 回转过程中螺旋桨的负荷变化机理分析
舰船在回转的过程中,由于侧向速度和角速度的存在,造成阻力的增加,使得航速下降,从而引起螺旋桨来流速度减小。假设螺旋桨的转速不变,则进速系数J会随着舰船航速的下降而逐渐减小。根据螺旋桨的水动力性能特点(图1[4]),当J减小时,会引起螺旋桨推力系数KT和转矩系数KQ增加,即螺旋桨的推力 XP和转矩Q增加[5-6]。然而在实际情况中,由于主机功率有限,螺旋桨的转矩不可能随着进速的减小而不断增加,而是需要根据主机所能提供的最大功率逐渐降低转速[7-8]。由于在设计航速时所取的计算点是螺旋桨效率的最高处,螺旋桨的效率会随着进速的减小而减小,在输入功率一定的情况下,输出的效率会逐渐降低。因此,按照等转速法进行舰船操纵性计算,会因计算中螺旋桨推力选取较大而对纵向速度、舵上来流速度等参数的计算结果造成影响,尤其对速降的计算结果影响较大,理论上速降的计算结果会偏小(即稳定状态下的纵向速度偏大)。
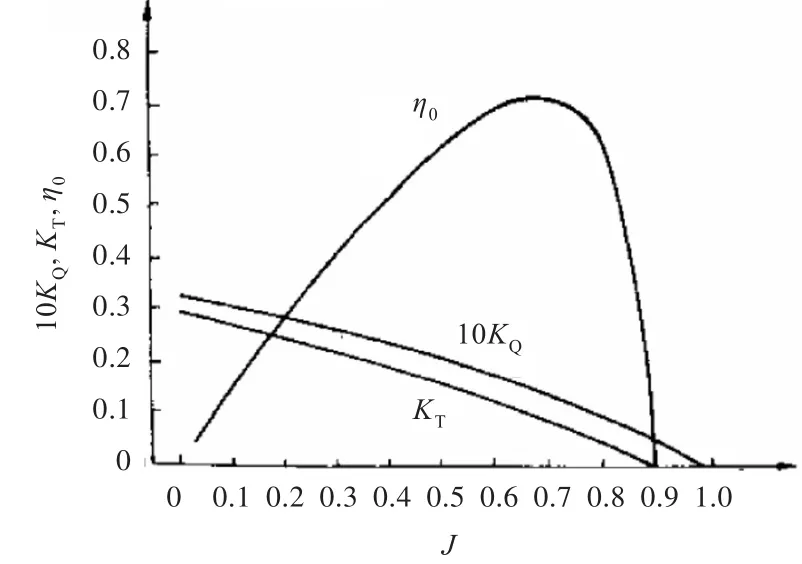
图1 螺旋桨敞水性征曲线Fig.1 Open water curves
此外,双桨船在回转过程中由于两桨距回转中心的距离不同,引起两桨的来流速度不同,导致螺旋桨的进速系数也不同,使得两桨的推力产生差异,从而产生转艏力矩。而采用等推力法计算时,由于无法反映出两桨推力的差异从而对回转直径的计算结果造成影响。理论上,内桨由于来流速度低于外桨,内桨的进速系数小于外桨,使得定常回转时内桨的负荷大于外桨[9-11],从而产生低于舰船回转的转矩。由于采用等推力法时无法反映这一情况,因此按照等推力法计算得到的舰船定常回转直径会小于实船的实际情况。
2 双桨船操纵性数学模型
2.1 运动坐标系
在研究船舶的操纵性运动时,通常采用2个坐标系[12],一个是固定于地球上的固定坐标系Eξηζ,另一个是固定于船体上与船体一起运动的运动坐标系oxyz,其原点与船舶重心G重合(图2)。
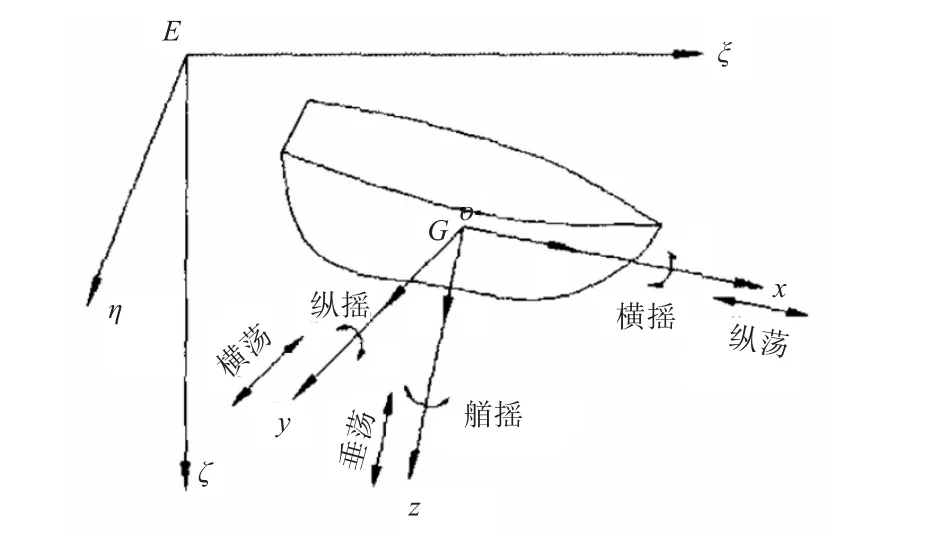
图2 舰船运动坐标系Fig.2 Coordinates of ship motion
2.2 MMG数学模型
假定舰船航行于无限深广的水域中,船体为刚体,自由面为静水,忽略船的纵摇和升沉,可提出计算所采用的四自由度MMG运动方程如式(1)所示:
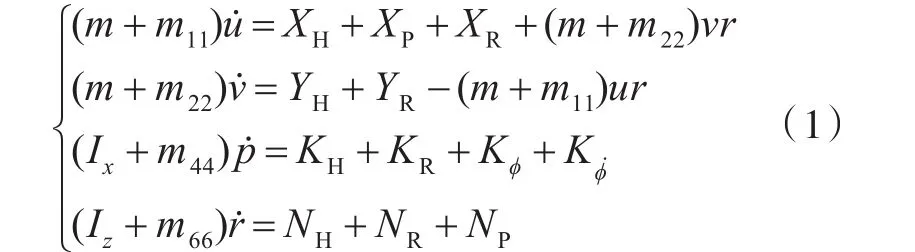
2.3 附加质量
m11,m22和 m66可用元良公式来表示(式(2),式(3)和式(5)),m44可用杜埃尔公式来表示(式(4)):
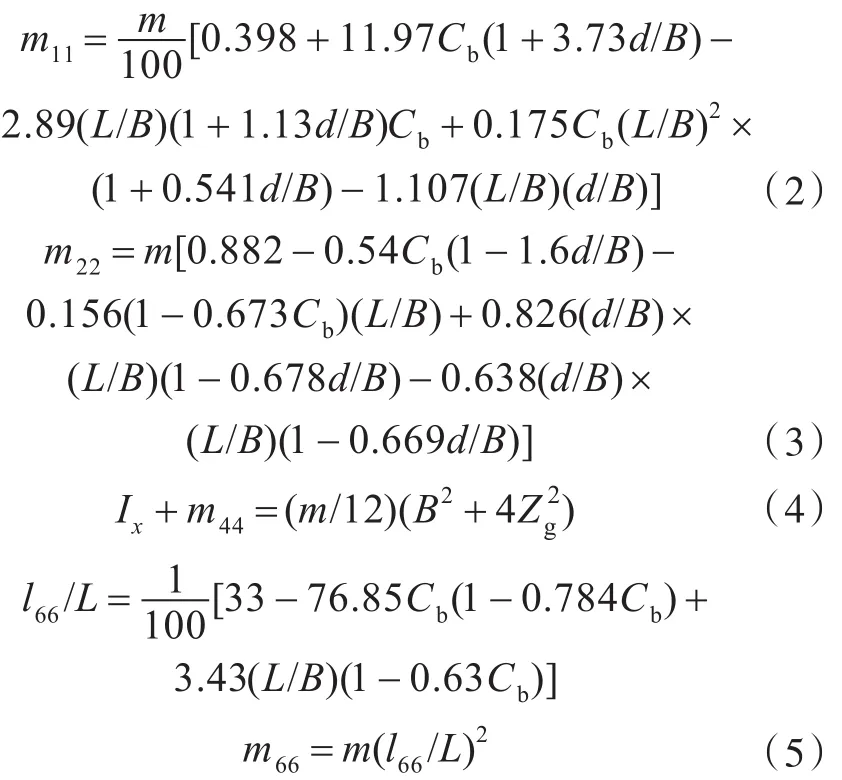
式中:L为船长;B为船宽;d为吃水;Cb为方形系数;Zg为重心高;l66为质量惯性半径。
2.4 船体水动力
纵向的船体水动力可表示为纵向速度的展开式,如式(6)所示:
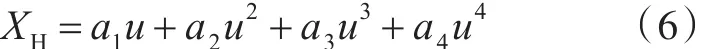
船体操纵的水动力如式(7)所示:
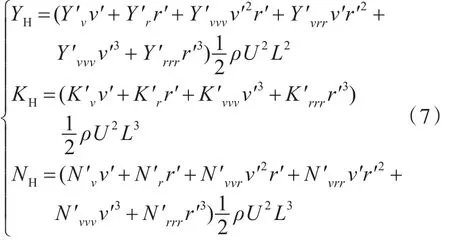
式中:ρ为流体密度;U为船运动速度;Y′v,Y′r,Y ′vvr,Y ′vrr,Y ′vvv,Y ′rrr,K ′v,K ′r,K ′vvv,K ′rrr,N ′v,N′r,N′vvr,N′vrr,N′vvv,N′rrr为操纵性水动力导数,可利用模型试验确定。
2.5 螺旋桨水动力
双桨船的螺旋桨推力 XP如式(8)所示:
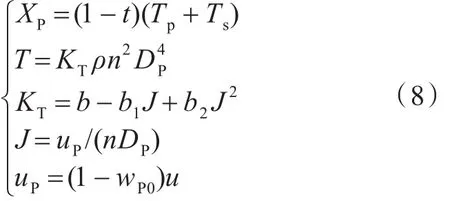
式中:t为推力减额系数;n为螺旋桨转速;DP为螺旋桨直径;wP0为伴流分数;Tp表示左桨推力;Ts表示右桨推力。
双桨船因两桨推力的差异所产生的转艏力矩NP如式(9)所示:

式中,yP为螺旋桨横向安装距离。
双桨船的螺旋桨转矩QP如式(10)所示:
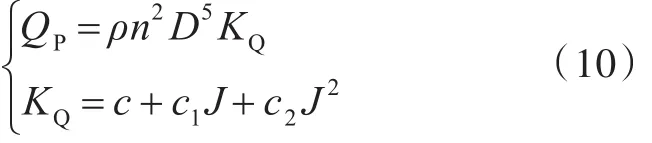
式中,KQ为扭矩系数。
上述各项水动力导数均可利用模型试验确定。
在采用等转速法进行螺旋桨推力的计算时,螺旋桨转速n取常数;在采用等推力法进行计算时,左右螺旋桨的推力 XP取常数;在采用等功率法计算时,左右螺旋桨的转速根据螺旋桨收到功率进行计算,进而计算出螺旋桨的推力,螺旋桨收到的功率取常数。
2.6 舵水动力
双舵船舵的法向力FN如式(11)所示:
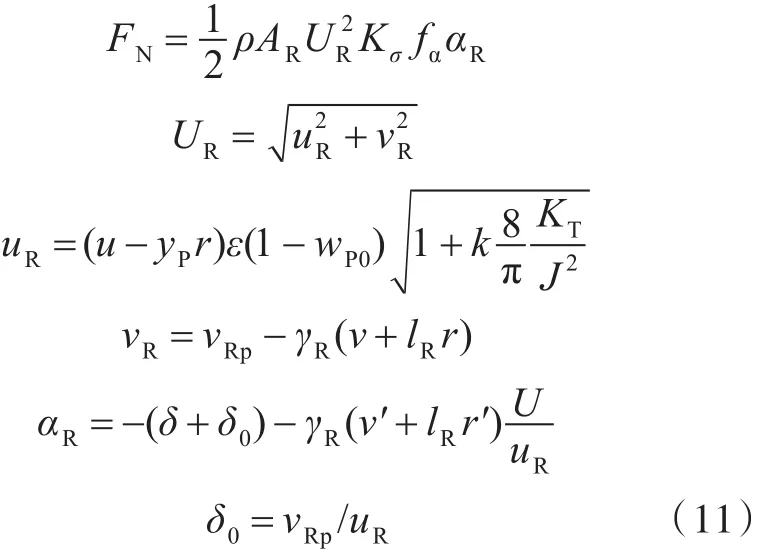
式中:AR为舵面积;UR为舵上的来流速度;Kσ为空泡对舵法向力的影响系数;fα为舵法向力导数对舵法向力的影响系数;ε为螺旋桨处伴流与舵处伴流比;αR为舵上的来流攻角;γR为船体整流系数;lR为旋转整流系数;δ0为压舵角。
3 双桨船操纵性预报
根据上述操纵性数学模型,分别采用等转速法、等推力法和等功率法进行某双桨双舵船在最大设计航速下,分别以操舵角 δ为-15°,-25°和-35°进行回转性预报,回转轨迹预报结果见图3~图5。双桨双舵船进入稳定回转后采用各方法得到的螺旋桨推力计算结果见表1,回转时速降的预报结果见表2,回转时两桨所产生的转艏力矩计算结果见表3。
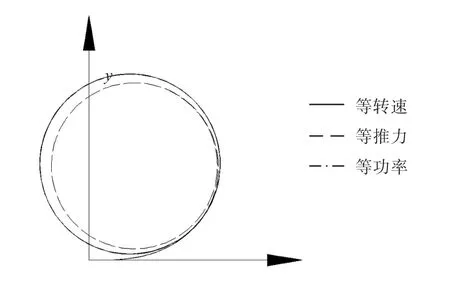
图3 船舶回转轨迹图(δ=15°)Fig.3 Schematic of the ship in turning motion( δ=-15°)
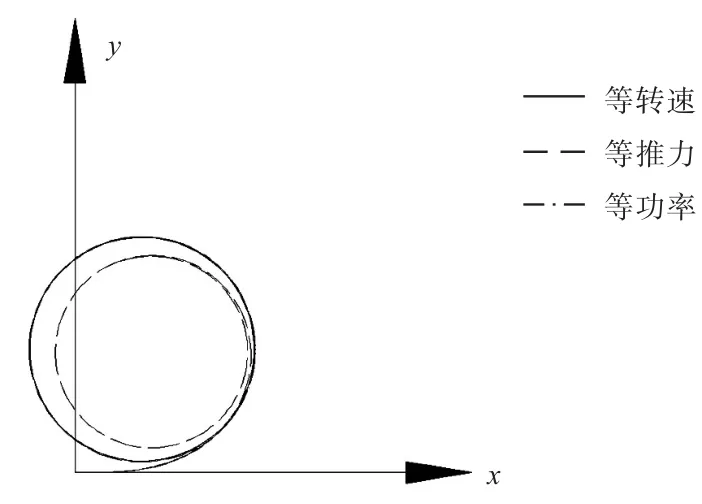
图4 船舶回转轨迹图(δ=-25°)Fig.4 Schematic of the ship in turning motion( δ=-25°)
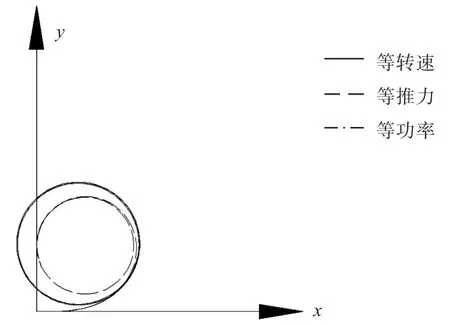
图5 船舶回转轨迹图(δ=-35°)Fig.5 Schematic of the ship in turning motion( δ=-35°)
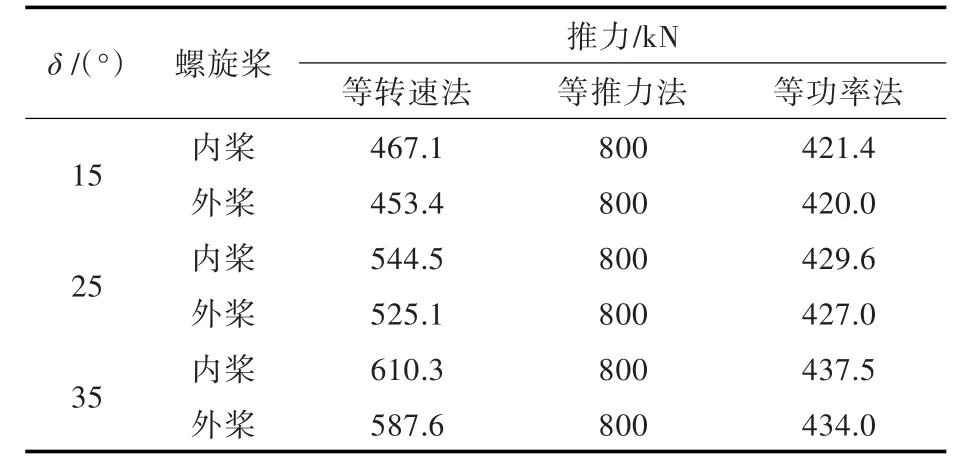
表1 回转时的螺旋桨推力计算结果对照表Tab.1 Contrast of thrust in turning motion
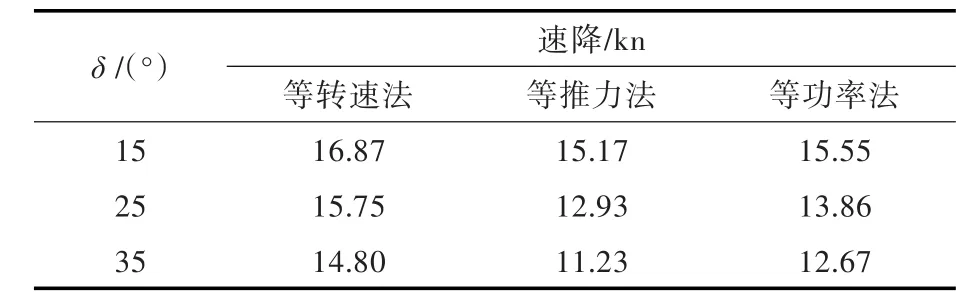
表2 回转时18 kn航速下的速降计算结果对照表Tab.2 Contrast of velocity in turning motion
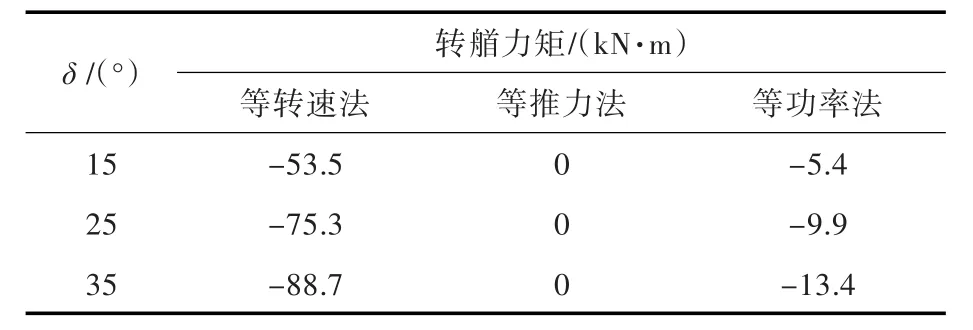
表3 回转时两桨所产生的转艏力矩计算结果对照表Tab.3 Contrast of moment coursed by twin propellers in turning motion
从图3~图5可以看出,采用等功率法在各操舵角时所得到的回转直径与采用等转速法时基本相同,均大于采用等推力法时的回转直径;采用等功率法在各操舵角时所得到的稳定时的纵向速度介于等转速法和等推力法之间,其中,等转速法所得到的速降最小,等推力法得到的速降最大;采用等转速法和等功率法均产生了反向的转艏力矩,其中等转速法在各操舵角时所产生的转艏力矩明显大于等功率法。这一情况与前述关于螺旋桨的负荷变化对于舰船回转直径及速降的影响分析结果是一致的。
接下来,就各方法计算得到的无因次回转直径和速降与实船的测试结果进行对比分析,对照情况见表4,图6和图7。
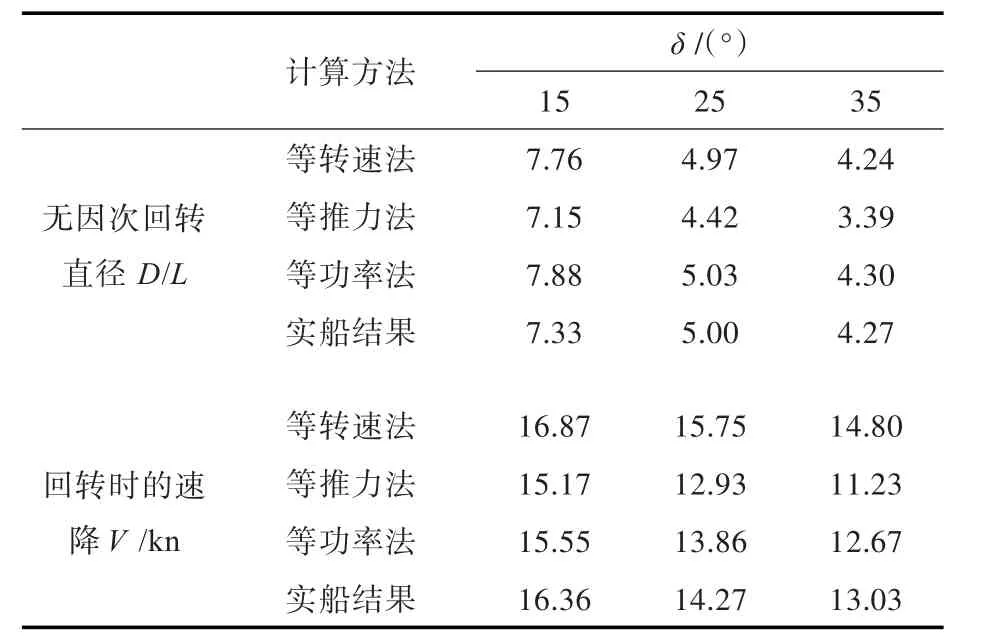
表4 回转时的计算结果与实船测试结果对照表Tab.4 Contrast of calculation and fact in turning motion
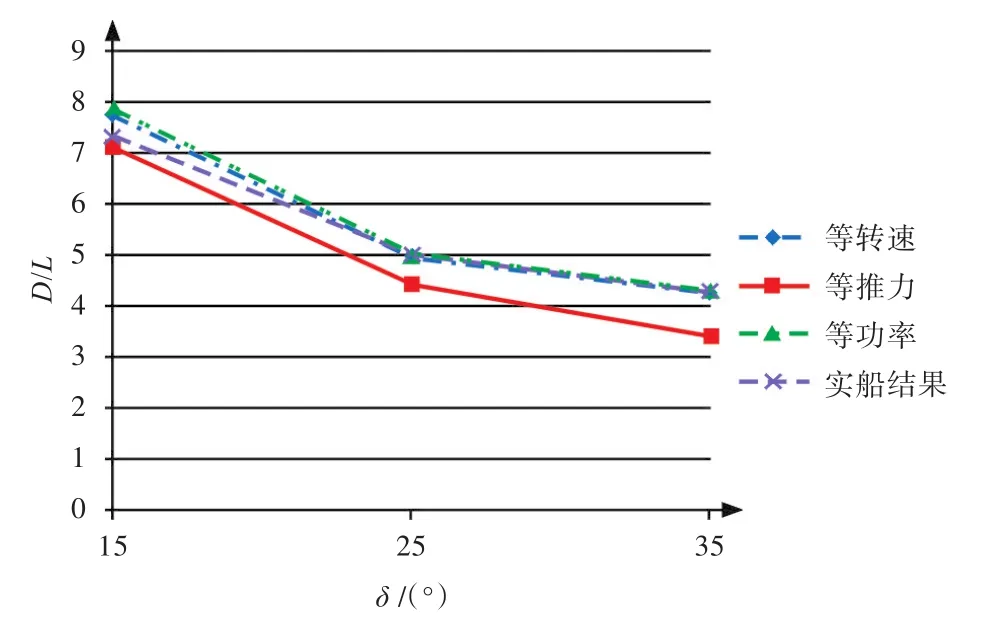
图6 回转时的相对回转直径对照图Fig.6 Contrast of diameters in turning motion
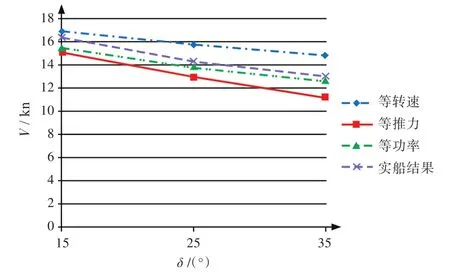
图7 回转时的速降对照图Fig.7 Contrast of velocities in turning motion
从上述对比可以看出,采用等转速法和等功率法所得到的相对回转直径在舵角较大时与实船实测结果基本相符,中小舵角时稍大于实船的实测结果,而采用等推力法所得到的相对回转直径的计算结果均小于实船实测结果;由图7可以看出,采用等转速法所得到的速降小于实船实测结果,且随着舵角的增大其差异逐渐增大;采用等推力法所得到的速降均大于实船实际结果,且随着舵角的增大其差异逐渐减小;采用等功率法所得到的速降略小于实船实测结果,且随着舵角的增大其差异逐渐减小。三种计算方法中,采用等功率法所得到的结果与实船实测结果最为接近。由此可见,采用等功率法进行双桨船操纵性的计算无论是在回转直径还是在速降方面都能达到最优的计算结果。
4 结 论
本文通过以上分析,得出以下结论:
1)与等转速法和等推力法相比,采用等功率法计算双桨船回转过程中内、外两桨的推力更接近实船螺旋桨的实际负荷情况,也更能反映螺旋桨对于舰船回转的影响;
2)采用等功率法计算得到的双桨船回转轨迹与采用等转速法的结果基本相同,与实船实际情况的符合性较好;
3)采用等功率法计算得到的双桨船回转时的速降介于等转速法和等推力法之间,与实船测试情况最为接近;
4)与等转速法和等推力法相比,采用等功率法计算得到的双桨船操纵性的计算结果与实船实际情况的吻合度更高。
[1]ABRAMOWSKI T.Prediction of propeller forces during ship maneuvering[J].Journal of Theoretical and Applied Mechanics,2005,43(1):157-178.
[2]邓爱民,朱伟.高速排水艇回转性能估算[J].中国舰船研究,2007,2(4):10-13.
DENG Aimin,ZHU Wei.Calculation of turning motion for high-speed displacement vessel[J].Chinese Journal of Ship Research,2007,2(4):10-13.
[3]王化明,邹早建.双桨双舵船舶操纵性预报研究[J].武汉理工大学学报(交通科学与工程版),2006,30(1):124-127.
WANG Huaming,ZOU Zaojian.Manoeuvrability prediction for a ship with twin propellers and twin rudders[J].Journal of Wuhan University of Technology(Transportation Science&Engineering),2006,30(1):124-127.
[4]盛振邦,刘应中.船舶原理(下)[M].上海:上海交通大学出版社,2004.
[5]吴恒.船舶动力装置技术管理[M].大连:大连海事大学出版社,1999.
[6]吴恒,夏治生.轮机长业务[M].大连:大连海事大学出版社,2000.
[7]覃峰,詹志刚,杨波,等.基于遗传算法的船舶推进系统船、机、桨匹配优化设计[J].武汉理工大学学报(交通科学与工程版),2003,27(1):50-52.
QIN Feng,ZHAN Zhigang,YANG Bo,et al.Genetic algorithm-based optimization design for match of ship,engine and propeller[J].Journal of Wuhan University of Technology(Transportation Science&Engineering),2003,27(1):50-52.
[8]AI H L,SHI D F.The research on the matching design of the ship-engine-propeller based on multi-objective particle swarm optimization[C]//Intelligent Systems and Applications(ISA).Wuhan,China,2010:1-4.
[9]洪剑飞.舵角和航速影响下的船舶操纵运动建模与仿真[D].大连:大连海事大学,2010.
[10]范尚雍,程智斌,吕韶康.高速双桨双舵船的船-桨-舵之间的水动力干扰[J].中国造船,1989(2):25-32.
FAN Shangyong,CHENG Zhibin,LV Shaokang.Hydrodynamic interaction between hull,propeller and rudder of high speed twin-screw,twin-rudder ships[J].Shipbuilding of China,1989(2):25-32.
[11]范尚雍,吕韶康,程智斌.双桨双舵船模系列斜拖试验研究[J].中国造船,1988(1):36-45.
FAN Shangyong,LV Shaokang,CHENG Zhibin.Oblique towing test results of a series of twin-screw,twin-rudder ship models[J].Shipbuilding of China,1988(1):36-45.
[12]HAMAMOTO M,MOON J K.A new coordinate system and the equations describing maneuvering of a ship in waves[J].Journal of the Society of Naval Architects of Japan,1993,173(6):209-220.
Maneuverability Prediction for Twin-Screw Ships by Considering the Loads of Screws
HU Xiaofang1,CHEN Songlin2
1 China Ship Development and Design Center,Wuhan 430064,China 2 Naval Armamemt Department of PLAN,Beijing 100841,China
By analyzing the effects of inboard and outboard screws changes of twin-screw ship on the ship's overall turning performance and velocity decline,this paper first presents a method to calculate the rotation speed,thrust coefficient,etc.,and the thrusts of screws as well as the turning moment of the ship are then confirmed,which leads to the calculation of the turning course and ship velocity.Taking a twin-screw ship as an example,the paper calculates its turning courses,thrusts,velocity,and turning moment by maintaining the rotation speed,thrust,and torque of the screw.Results show that the turning course calculated with constant rotation speed and constant torque are almost identical,and are quite close to reality;the velocity decline calculated with constant torque is between the one obtained with the other two approaches,and is seen to resemble most to reality.
maneuverability;MMG model;twin-screw ship;screw;load
U661.33
A
1673-3185(2014)02-17-05
10.3969/j.issn.1673-3185.2014.02.004
http://www.cnki.net/kcms/doi/10.3969/j.issn.1673-3185.2014.02.004.html
期刊网址:www.ship-research.com
2013-07-09 网络出版时间:2014-3-31 16:32
胡晓芳(1979-),女,工程师。研究方向:船舶装置与舾装设计。E-mail:5795808@qq.com
陈松林(1964-),男,硕士。研究方向:舰船总体研究与设计
胡晓芳
[责任编辑:胡文莉]
