基于舱段模型的大开口甲板结构稳定性分析与设计

周于程，郑绍文，刘均，郑杰，程远胜

1华中科技大学船舶与海洋工程学院，湖北武汉430074 2中国舰船研究设计中心，湖北武汉430064

基于舱段模型的大开口甲板结构稳定性分析与设计

周于程1，郑绍文2，刘均1，郑杰2，程远胜1

1华中科技大学船舶与海洋工程学院，湖北武汉430074 2中国舰船研究设计中心，湖北武汉430064

针对某大开口舱段结构，采用有限元方法（FEM）对比分析3种计算模型位移载荷作用下第1层甲板纵骨轴向应力的分布。计算结果表明，该应力分布存在较大程度的不均匀性，采用双层板架模型或立体舱段模型能获得较准确的纵骨轴向应力分布。同时，分析2种基于稳定性要求的大开口甲板纵骨设计理念的优劣。为合理利用结构材料，均衡各区域纵骨的稳定性储备，建议在设计甲板纵骨时要考虑大开口甲板纵骨轴向应力分布的不均匀性。

大开口舱段结构；甲板纵骨稳定性；纵骨轴向应力分布；有限元法

0 引 言

船舶甲板结构的稳定性一直是设计者关注的问题。吴广明［1］介绍了ANSYS中线弹性结构稳定性问题的计算理论及方法，认为采用交叉梁系模型更易于获得板架结构的整体稳定性。于杰［2］对加筋板结构承受面内载荷的各种失稳模式进行了较详细的分析。Byklum等［3］基于Marguerre非线性板理论，提出了一种分析加筋板整体屈曲的半解析计算模型。刘彦峰［4］针对单向受压密加筋板，推导出了结构整体失稳时的临界载荷实用计算公式。Peng等［5］基于一阶剪切变形理论，提出了一种用于分析加筋板稳定性问题的无网格伽辽金法。李政杰［6］计算分析了开孔加筋板的稳定性，指出开孔会降低加筋板的屈曲强度，且随着开孔尺寸的增加，屈曲强度逐渐降低。

针对大开口甲板结构的稳定性，张宇力等［7］对比分析了开口与不开口甲板板架结构的稳定性，计算结果表明，大开口对甲板板架稳定性影响较大。李小灵等［8］对比分析了采用相当板法和相当梁系方法估算开口区域纵向构件应力的差异，发现采用相当梁系方法所得的结果低于相当板方法的，比较接近于有限元计算结果，可作为大开口船舶板架受力状况的计算方法，并提出了大开口区域结构补强方法。

上述文献采用的计算模型均为单层板架模型，且舷侧或纵舱壁对甲板板架的支撑作用被处理为了简支。本文将针对某大开口舱段结构，对比分析采用全舱段立体模型、双层板架模型和单层板架模型计算甲板纵骨轴向应力分布的差异性，同时，还将分析2种基于稳定性要求的大开口甲板纵骨设计理念的优劣。为合理利用结构材料，提出在设计大开口甲板纵骨时，应考虑沿船宽方向、纵骨轴向应力分布的不均匀性。设计时，可运用单跨梁临界失稳应力理论计算公式来初定纵骨尺寸。

1 位移载荷下大开口舱段结构应力有限元分析

1.1 大开口舱段结构有限元建模

选取某船舶三舱段结构作为分析对象，其典型特征是中间舱段第1层、第2层甲板设有大开口，其横截面如图1所示。三舱段结构总长L=30 m，宽 B=18.36 m，型深 D=11.3 m，大开口宽9.12 m，第1层（顶层）甲板结构布置如图2所示。材料弹性模型 E=200 GPa，泊松比 μ=0.3，材料密度 ρ=7 800 kg/m3。

本文采用大型通用有限元分析软件ANSYS 12.1分析该三舱段结构在边界位移载荷下的第1层甲板纵骨轴向内力分布。有限元模型中，甲板板、舷侧外板、外底板、肋板、龙骨以及甲板强骨材腹板采用板壳单元Shell 181模拟，甲板纵骨、甲板强骨材面板和舷侧纵骨等采用梁单元Beam 188模拟，有限元模型如图3（a）所示。本文的板架稳定性分析主要关注第1层甲板纵骨的失稳临界应力，为避免出现过多的板格失稳波形，将纵骨间板格划分为2个单元，共划分125 273个板壳单元。

图1 舱段结构横截面示意图Fig.1 The cross-section of the middle cabin structure

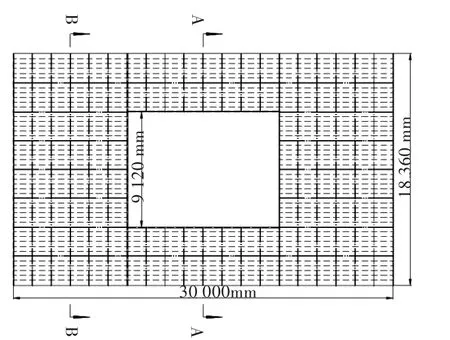
图2 第1层甲板结构布置图Fig.2 The structural layout plan of the first deck

考虑到不同计算模型沿船宽方向甲板纵骨轴向应力分布的差异，本文还分析了2个计算模型：双层板架模型（选取立体舱段结构第1层甲板和第2层甲板，以及两层甲板间的纵横舱壁和舷侧结构，如图3（b）所示）和单层板架模型（只选取立体舱段结构第1层甲板结构，如图3（c）所示）。

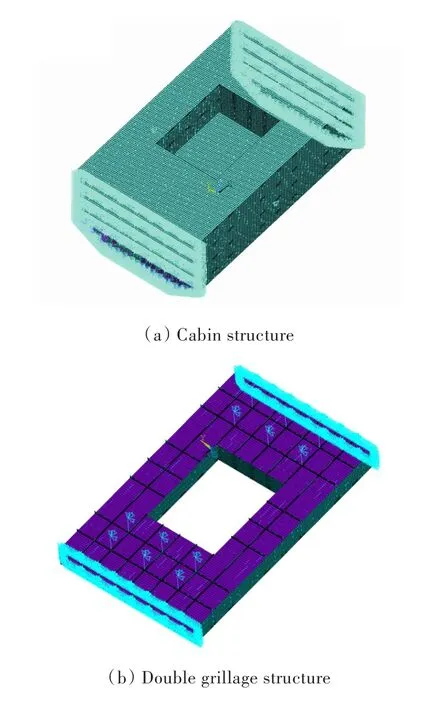
图3 三舱段结构有限元模型Fig.3 The FEM model of a three-cabin structure

为了使舱段模型分析符合全船总纵弯曲的实际状态，根据总纵弯曲的平断面假定，即纵向工作应变为均匀压缩应变，施加沿型深方向线性分布的端部位移载荷以模拟总纵弯曲，并对边界条件作适当处理。3种计算模型的位移载荷施加示意图以及边界条件的处理方式如表1所示。

1.2 不同计算模型下第1层（顶层）甲板纵骨轴向应力分布对比

3种计算模型第1层甲板开口区域（剖面A-A）沿船宽方向的纵骨轴向应力分布如图4所示。

表1 计算模型边界条件及载荷施加方式Tab.1 Boundary conditions and applied load of computational models

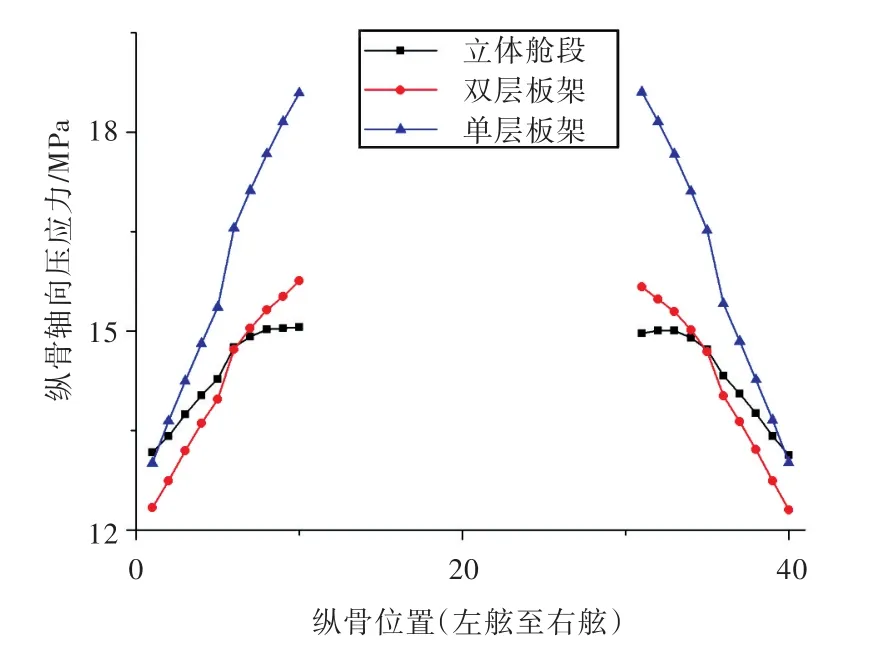
图4 大开口区域第1层甲板纵骨轴向应力分布Fig.4 The axial stress distribution of the longitudinals at the first deck in the region with a large opening

由图可看出，双层板架结构计算模型和立体舱段结构计算模型沿舷侧至开口区域，其纵骨轴向应力呈抛物线增长趋势，靠近开口区域的纵骨轴向应力达到最大值，2个模型的纵骨轴向应力分布比较接近；而单层甲板板架结构计算模型沿舷侧至开口区域，其纵骨轴向应力增长速度快且幅度大，应力分布的不均匀性程度较其它2种计算模型的高，其主要原因是单层板架模型没有考虑纵舱壁在船长方向提供的纵向刚度。3种计算模型第1层甲板开口区域（剖面A-A）沿船宽方向的纵骨轴向应力最大值如表2所示。

表2 开口区域第1层甲板纵骨轴向应力最大值Tab.2 The maximum longitudinal axial stress at the first deck in the region with a large opening

3种结构计算模型第1层甲板非开口区域（剖面B-B）沿船宽方向的纵骨轴向应力分布如图5所示。

由图可知，在甲板非大开口区域，3种结构计算模型所获得的纵骨轴向应力分布规律比较接近，沿船宽方向呈抛物线分布。舷侧附近的纵骨轴向应力约为船舯区域纵骨轴向应力的5倍，但和大开口附近的纵骨轴向应力相比要小。

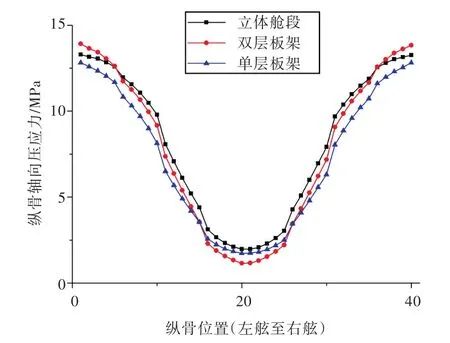
图5 非大开口区域第1层甲板纵骨轴向应力分布Fig.5 The axial stress distribution of the longitudinals at the first deck in the region without large opening

综上分析，可采用双层板架模型或立体舱段模型来计算大开口甲板纵骨轴向应力的分布。本文后续将采用立体舱段模型计算结果进行纵骨设计。

2 大开口甲板纵骨设计

2.1 大开口甲板纵骨设计理念

在按规范对甲板板架结构进行稳定性校核时，一般要求结构纵向骨架的理论欧拉应力与其材料屈服极限之比大于某一特定值。强力甲板骨架构件中的带板纵骨在舯部0.5倍设计水线长范围内，其理论欧拉应力σe与其所用材料屈服应力σs之比大于 2.0，在端部大于 1.5［9］。为便于说明问题，本文将所研究的立体舱段第1层甲板分为了3个区域，如图6所示。目前，存在2种大开口甲板纵骨设计理念。

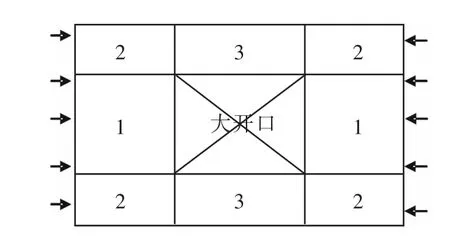
图6 第1层甲板区域划分Fig.6 Region division of the first deck

理念1：低纵骨轴向应力区域，即图6所示非开口区域1，其纵骨稳定性满足规范所要求的稳定性储备系数（即理论欧拉应力大于或等于1.5σs），而高纵骨轴向应力区域，包括图6所示的非开口区域2和开口区域3，其纵骨临界应力则分别为区域1纵骨临界应力乘上相应区域纵骨轴向应力不均匀程度系数（类似于应力集中系数），但不超过材料的屈服应力。

理念2：大开口甲板整个区域的纵骨稳定性均按规范要求的稳定性储备系数设计，即整个甲板纵骨的理论欧拉应力大于或等于1.5σs。

板架开口区域因为结构突然中断，承载结构变少，因而其纵骨轴向应力明显比非开口区域的纵骨轴向应力高，且沿船宽方向纵骨的轴向应力分布存在较大程度的不均匀性（图4、图5）。设计理念1能保证甲板纵骨的稳定性储备均衡、匹配，满足规范要求。虽然开口区域甲板的纵骨稳定性储备有富裕，结构重量有所增加，但按照理念1的设计可有效提高大开口甲板开口区域结构的极限承载能力。

设计理念2满足目前规范对强力甲板骨材稳定性的要求，但未考虑甲板纵骨轴向应力分布的不均匀性，其开口区域的实际压应力会大于其它区域，开口区域的纵骨会先于非开口区域的纵骨失稳，开口区域的剖面极限承载能力低于非开口区域，结构承载能力出现薄弱区，存在设计上的“短板”。依据理念2设计的甲板其纵骨稳定性储备不匹配，材料不能得到充分利用。

为合理利用结构材料，在设计艏、艉部大开口甲板板架纵骨时，应考虑大开口甲板不同区域纵骨轴向应力分布的不均匀程度。从规避局部结构破坏风险的角度出发，进行大开口甲板纵骨设计时，宜优先采用设计理念1。

2.2 大开口甲板纵骨设计方法

下面，将以第1层甲板为例来说明2种设计理念下某大开口甲板板架纵骨尺寸的估算方法。

2.2.1 理念1大开口甲板纵骨设计方法

以区域1甲板纵骨轴向应力最大的纵骨为设计基础，其理论欧拉应力大于1.5倍的材料屈服极限，依据材料欧拉应力修正曲线，此时，区域1的甲板纵骨临界应力σcr约为 k（本文取 k=0.9）倍的材料屈服极限。根据前面所述的甲板纵骨轴向应力分布规律，区域2和区域3的甲板纵骨临界应力应分别大于k1k倍和k2k倍的材料屈服极限，其中k1为区域2和区域1的纵骨轴向应力最大值之比，k2为区域3和区域1的纵骨轴向应力最大值之比，其值取决于结构的具体布置和尺寸搭配。针对具体的结构，可通过有限元计算得到。对于本文考虑的立体舱段结构计算模型，k1和k2的取值如表3所示。

2.2.2 理念2大开口甲板纵骨设计方法

3个区域的甲板纵骨理论欧拉应力大于材料屈服极限的1.5倍即满足设计要求。

2.2.3 大开口甲板纵骨设计方案

对于甲板纵骨，其理论欧拉应力（单位MPa）可按两端简支单跨梁模型进行计算，如式（1）所示［10］：

式中：i为包括带板的纵骨剖面惯性矩，mm4；a为纵骨跨距（横梁间距），mm；f为不包括带板的纵骨剖面积，mm2；be为纵骨间距，mm；t为带板厚度，mm；E为材料弹性模量，MPa。

对于第1层甲板，a=1 500 mm，t=8 mm，不失一般性。当甲板纵骨采用100×6型球扁钢时，纵骨理论欧拉应力σe（801.860 MPa）为1.5倍的材料屈服极限，刚好满足设计要求，此时，纵骨的临界应力σcr约为0.9倍的材料屈服极限。

基于理念1，区域1的甲板纵骨采用100×6型球扁钢，区域2的甲板纵骨临界应力应不小于k1σcr，区域3的甲板纵骨临界应力应不小于 k2σcr，根据材料欧拉应力修正曲线，插值获取各区域甲板纵骨要求的欧拉应力，进而运用单跨梁失稳应力理论计算值确定甲板纵骨的型号。若甲板纵骨设计要求的临界应力超过材料屈服极限，则纵骨临界应力值直接取材料屈服极限值。在对甲板区域3的结构进行设计时，可通过增大骨材型号或减小横梁间距的方式来提高甲板纵骨的临界失稳应力，其中，减小横梁间距的方案需考虑在舷侧（纵舱壁）相应位置增设垂直扶强材以形成空间框架结构。具体采用何种方案，可综合考虑结构布置、重量和工艺等因素后酌情定夺。满足设计要求的方案如表3所示。

基于理念2，3个区域的甲板纵骨均采用100×6型球扁钢。

表3 依理念1的第1层甲板纵骨设计方案Tab.3 The design scheme of the first deck longitudinals based on idea No.1

3 结 论

本文采用有限元方法对比分析了某大开口舱段结构3种不同计算模型位移载荷作用下第1层（顶层）甲板纵骨轴向应力的分布，提出了基于稳定性要求合理设计甲板纵骨的方法，主要结论如下：

1）立体舱段计算模型、双层甲板计算模型和单层甲板计算模型的计算结果均表明，在端部位移载荷作用下，大开口区域沿船宽方向甲板纵骨的轴向应力分布存在较大程度的不均匀性，其中由单层甲板计算模型得到的纵骨轴向应力分布的不均匀性程度最大，而由立体舱段和双层甲板计算模型得到的纵骨轴向应力分布的不均匀性程度比较接近；对于非大开口区域沿船宽方向的甲板纵骨，由3种计算模型得到的纵骨轴向应力分布的不均匀性程度比较接近。因此在进行实际计算时，建议采用双层板架模型或立体舱段模型进行大开口甲板纵骨轴向应力分布计算。

2）设计理念1能保证甲板纵骨的稳定性储备均衡、匹配，同时，还可有效提高甲板结构的极限承载能力；设计理念2满足目前规范对强力甲板骨材稳定性的要求，但开口区域与非开口区域甲板纵骨的稳定性储备不匹配，材料未得到充分利用。为合理利用结构材料，在进行甲板纵骨设计时，应考虑大开口甲板不同区域纵骨轴向应力分布的不均匀程度。为规避局部结构破坏的风险，进行大开口甲板纵骨设计时，宜优先采用设计理念1。

［1］吴广明.用ANSYS进行甲板板架稳定性计算［J］.中国舰船研究，2007，2（2）：5-8.

WU Guangming.Stability calculation of deck grillage using ANSYS software［J］.Chinese Journal of Ship Re⁃search，2007，2（2）：5-8.

［2］于杰.面内荷载作用下船体结构的稳定性分析［D］.武汉：武汉理工大学，2005.

［3］BYKLUM E，STEEN E，AMDAHL J.A semi-analyti⁃cal model for global buckling and postbuckling analy⁃sis of stiffened panels［J］.Thin-Walled Structures，2004，42（5）：701-717.

［4］刘彦峰.密加筋板结构强度和稳定性的力学性能分析与结构设计［D］.武汉：武汉理工大学，2006.

［5］PENG L X，LIEW K M，KITIPORNCHAI S.Buckling and free vibration analyses of stiffened plates using the FSDT mesh-free method［J］.Journal of Sound and Vi⁃bration，2006，289（3）：421-449.

［6］李政杰.开孔加筋板的强度和稳定性及其极限强度力学性能分析［D］.武汉：武汉理工大学，2012.

［7］张宇力，曾广武，段洪，等.大开口对船舶板架稳定性和极限承载力的影响［J］.华中科技大学学报（自然科学版），2002（5）：56-58，64.

ZHANG Yuli，ZENG Guangwu，DUAN Hong，et al.The effect of big placket on stability and terminal load⁃ing in marine structure［J］.Journal of Huazhong Uni⁃versity of Science and Technology（Nature Science Edi⁃tion），2002（5）：56-58，64.

［8］李小灵，张宇力，曾广武，等.大开口船舶板架的稳定性分析及补强方法研究［J］.船海工程，2001（增刊2）：79-84.

［9］王晓强，陈崧，李陈峰，等.水面舰船规范中甲板纵骨稳定性校核的差异研究［J］.中国舰船研究，2012，7（2）：56-59.

WANG Xiaoqiang，CHEN Song，LI Chenfeng，et al.Dif⁃ference of deck longitudinal stability check between GJB 4000-2000 and GJB/Z119-99［J］.Chinese Jour⁃nal of Ship Research，2012，7（2）：56-59.

［10］王杰德.船体强度与结构设计［M］.北京：国防工业出版社，1995.

Stability Analysis and Design of Deck Grillage Structures with Large Opening Based on Cabin Models

ZHOU Yucheng1，ZHENG Shaowen2，LIU Jun1，ZHENG Jie2，CHENG Yuansheng1

1 School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China 2 China Ship Development and Design Center，Wuhan 430064，China

By examining the cabin structure with large opening，the longitudinal axial stress distribution under displacement load on the first deck is investigated with three different computational models，using the Finite Element Method（FEM）.Numerical results show that the axial stress distribution displays a het⁃erogeneity of large degree，and such distribution could be obtained with acceptable accuracy via either the double grillage structure model or the cabin structure model.Also，the advantages and disadvantages of two methodologies that can be applied on the longitudinal design of the first deck with large opening are an⁃alyzed based on their stability.In order to improve the material utilization and balance the stability require⁃ment for different regions of longitudinal，the non-uniformity of deck longitudinal axial stress distribution is advised to be considered for the design of deck longitudinal.

cabin structure with large opening；stability of deck longitudinal；axial stress distribution of deck longitudinal；Finite Element Method（FEM）

U661.4

A

1673－3185（2014）02－37－05

10.3969/j.issn.1673-3185.2014.02.007

http://www.cnki.net/kcms/doi/10.3969/j.issn.1673-3185.2014.02.007.html

期刊网址：www.ship-research.com

2013－11－06 网络出版时间：2014-3-31 16:32

国家部委基金资助项目

周于程（1989－），男，硕士生。研究方向：结构分析与优化。E-mail：yczhou1989@163.com

程远胜（1962－），男，博士，教授，博士生导师。研究方向：结构分析与优化，结构冲击动力学与防护设计，结构振动与噪声控制。E-mail：yscheng@hust.edu.cn

程远胜

［责任编辑：卢圣芳］