四元数在水下航行体运动建模中的应用
2014-07-19徐正武唐国元邓智勇黄道敏黄永忠
徐正武,唐国元,邓智勇,黄道敏,黄永忠
1华中科技大学船舶与海洋工程学院,湖北武汉430074 2武汉第二船舶设计研究所,湖北武汉430064 3空军预警学院电子对抗系,湖北武汉430019
四元数在水下航行体运动建模中的应用
徐正武1,唐国元1,邓智勇2,黄道敏3,黄永忠1
1华中科技大学船舶与海洋工程学院,湖北武汉430074 2武汉第二船舶设计研究所,湖北武汉430064 3空军预警学院电子对抗系,湖北武汉430019
针对一类以控制力矩陀螺(CMG)为姿态控制执行机构的水下航行体,考虑到其大角度机动时姿态描述矩阵可能会出现奇异的问题,建立了与其相适应的运动模型。首先,通过引入四元数来建立运动学方程,并给出四元数与欧拉角之间的关系。随后,在建立动力学方程时,将水下航行体视为由水下航行体和CMG组成的多刚体系统,并使用四元数来代替动力学方程中的欧拉角项。最后,使用龙格库塔法对所建立的模型进行仿真。仿真结果表明,所建立的模型能有效避免使用欧拉角方法建立模型时所产生的奇异问题。
四元数;控制力矩陀螺;水下航行体;运动模型
0 引 言
目前,大多数水下航行体均采用欧拉角方法来建立其运动学方程,而当水下航行体俯仰角出现±90°情况时,其运动学方程就会出现奇异[1]。由此可知,对于水面船舶和一些在垂直面内不进行大姿态角机动的水下航行体而言,采用欧拉角方法来建立其运动学方程完全可行。但是,随着水下航行体种类和功能的多样化,一些水下航行体在运动过程中会出现姿态角±90°的情况,如高空空投反潜鱼雷[2-3]。又如,以控制力矩陀螺(CMG)为姿态控制执行机构的水下航行体,由于其可以实现任意姿态角机动[4],故该水下航行体的俯仰角也完全有可能达到±90°附近。基于此,文献[5]提出将CMG作为水下航行体姿态控制执行机构,并进行实验验证。CMG的工作原理是依靠框架带动恒速飞轮转动使得飞轮的角动量方向发生改变,进而控制力矩,其具有力矩放大、输出力矩连续、执行机构内置[6]等诸多优点。同时,由于CMG可以输出3个自由度的力矩,故可以实现对任意姿态角的控制。并且,特别需要指出的是由于CMG在横摇方向能够输出力矩,所以其不必依靠横倾回复力矩来保证水下航行体的稳定性。这就意味着在给水下航行体进行配重时,可以将重心和浮心配置在同一高度,此时水下航行体在垂直面内做俯仰运动也就不受纵倾回复力矩作用。基于这一点,水下航行体在垂直面内的机动将更容易,即其俯仰角更容易达到±90°附近。
对于以CMG为姿态控制执行机构(其具体方法参见文献[3-4]和文献[7],限于篇幅,此处不再赘述)的水下航行体,由于其俯仰角会达到±90°附近,而采用欧拉角方法来建立其运动学方程会产生奇异,因此有必要采用其它方法来建立其运动学方程。本文拟采用四元数法来建立其运动学方程,同时在建立其动力学方程时还会使用四元数来代替方程中的姿态角项。
1 四元数
四元数由Hamilton于1843年提出,是一种超复数。但是,直到20世纪70年代,四元数才开始在控制工程中得到应用。运用四元数来描述水下航行体的姿态能够克服欧拉角奇异性的缺点,且其运算也不涉及复杂三角函数,因此非常适合实时在线计算。四元数包含一个三维矢量和一个标量。根据欧拉旋转定理[8],刚体绕固定点的任意位移可以绕通过此点的某一轴转动某一角度而得到。四元数的矢量部分就表示这一转动轴的方向,其标量部分则与绕转动轴转动的角度大小有关。因此,四元数可以定义为[8]
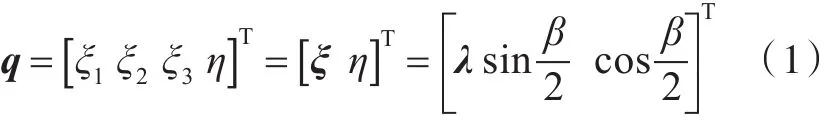
显然有
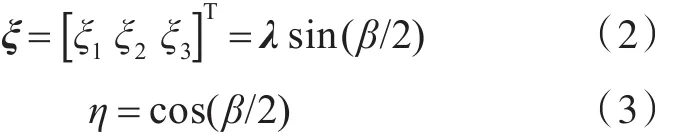
以上式中:λ为转动轴矢量(又叫欧拉轴矢量);β为绕转动轴转动的角度,(°);上标T为矩阵的转置,后文均沿用这种表示方法。
2 基于四元数的运动模型
2.1 坐标系及参数定义
如图1所示,描述一个水下航行体的运动通常需建立2个坐标系:与大地固连的惯性系OE-XEYEZE;与水下航行体固连的动坐标系Ob-XbYbZb。水下航行体的位置在惯性系下描述为η1=[x y z]T,水下航行体的姿态角(欧拉角描述)描述为 η2=[φ θ ψ]T。其中:φ为横摇角,(°);θ 为纵倾角,(°);ψ 为航向角,(°)。水下航行体的线速度在动坐标系下描述为 v1=[u v w]T,水下航行体的角速度在动坐标系下描述为v2=[p q r]T。其中:u为轴向速度,m/s;v为横漂速度,m/s;w为垂向速度,m/s;p为横摇角速度 ,(°)·s-1;q 为纵倾角速度,(°)·s-1;r为转艏角速度,(°)·s-1。
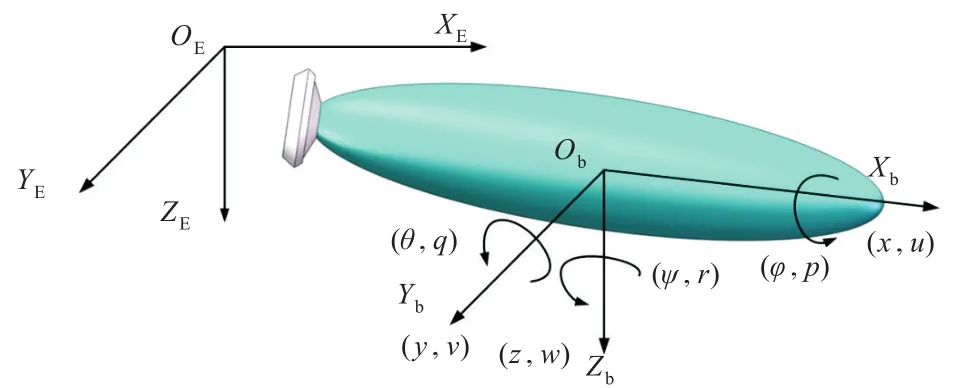
图1 水下航行体坐标系与运动参数Fig.1 Coordinate and motion parameters of an autonomous underwater vehicle
2.2 运动学方程
线速度矢量在惯性系下描述为η˙1,在动坐标系下描述为v1。由此,

式中:η˙1为对时间的导数;C ∈ R3×3,为动坐标系向惯性系变换的坐标变换矩阵。
根据欧拉旋转定理,动坐标系可以通过绕着某一轴转动某一角度,从而与惯性系重合。因此,式(4)中的C可以由下式给出:
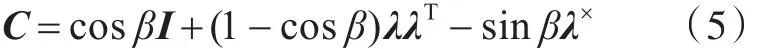
式中:I为3×3的单位矩阵;λ×为λ的反对称矩阵。将式(1)、式(2)和式(3)代入式(5),可得
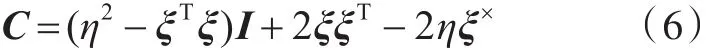
鉴于C完全由q决定,可将C记为 E1(q)。然后,展开式(6)可得
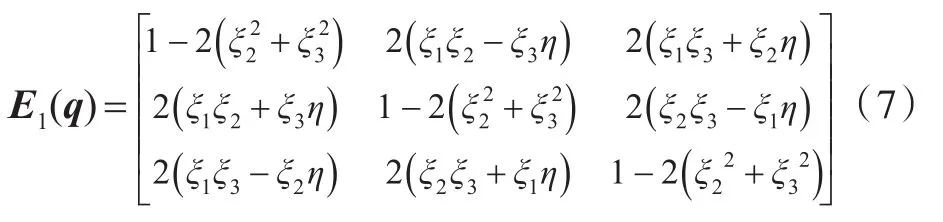
坐标变换矩阵C满足如下关系式[9]:

联立式(6)和式(7),可得
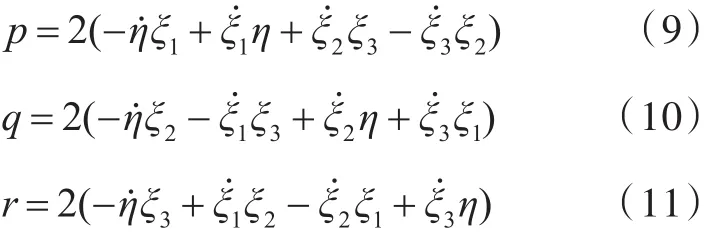
四元数q中的4个元素并不是独立的,必须满足以下关系:
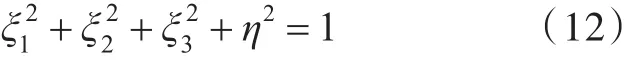
对式(12)两边微分,得

将式(9)~式(11)、式(13)写成矩阵的形式,并根据四元数的逆运算和乘法运算,有


将式(1)和式(14)写在一起,得
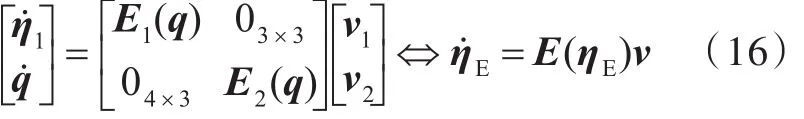


J2(η2)为姿态变换矩阵,则由下式给出:

对比式(16)和式(18),可以得到欧拉四元数与欧拉角之间有如下关系式:

对于式(19),当 θ=±90°时,J1(η2)陷入奇异,此时该方程无法描述水下航行体的姿态。但是,采用式(14)来描述水下航行体的姿态则不存在奇异问题。另外,由式(14)可以看出采用四元数建立的运动学方程的运算只涉及简单的乘法运算,并不涉及到复杂三角函数运算,从而更加适合在线实时运算。
2.3 动力学方程
将水下航行体视为由水下航行体本体与CMG组成的多刚体系统,利用动量定理和动量矩定理,并充分考虑其与水的相互作用力,可以推导出水下航行体的动力学方程。若采用欧拉角描述水下航行体的姿态,水下航行体的动力学方程中也会出现欧拉角。因此,本文利用式(20),并运用四元数来代替动力学方程中的欧拉角,可以得到下列动力学方程:

式中:τ为水下航行体所受到的控制力(力矩),包括螺旋桨的推力和CMG输出的控制力矩,可以通过相应的控制算法解算出来;f为水下航行体6个自由度上经过解耦后所受到的合力和力矩,可由下式给出:
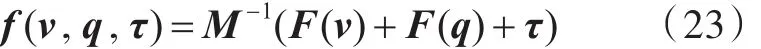
式中:M为水下航行体的质量、惯量(包含附连水)矩阵;F(v)为水下航行体所受到的水动力和科氏力以及CMG与水下航行体的耦合力;F(q)为水下航行体所受到的静力。M和F(v)的具体表达式见文献[5]和文献[10],F(q)由下式给出:
社会统计学与数理统计学的根本区别在于前者在统计研究中以事物的质为前提,强调认识事物质的重要性,后者则不关心事物的质.

式中:W和B分别为航行体所受到的重力和浮力,N;xG,yG和zG为航行体重心在动坐标系中的坐标,m;xC,yC和zC为航行体浮心在动坐标系中的坐标,m。
基于此,式(16)和式(22)便构成了基于四元数的运动模型。
3 计算机仿真
给定水下航行体的初始状态和控制输入,通过式(16)和式(22)便可仿真出水下航行体整个运动过程中的运动状态。为获得较好的仿真精度,本仿真算例利用龙格库塔法来求解式(16)和式(22),具体仿真方法如下:
1) n=0 。初始化 v(n),q(n),ηE(n),τ(n)。
2)由第n步的值递推出第n+1步的值。首先计算下列值:

其中,τ(n+0.5)=0.5(τ(n)+τ(n+1)),Δt为仿真步长。接着,就可以得到n+1步的值:
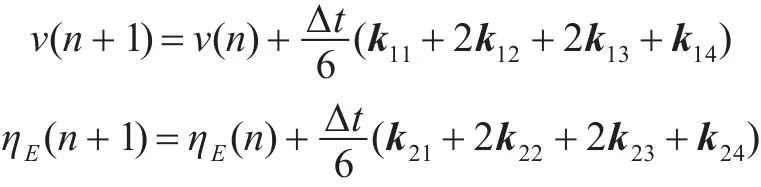
3)将q(n+1)单位化。理论上四元数q必须满足式(12),但是在数值计算时会存在一些误差,为了保证式(12)成立,有必要将q(n+1)单位化。单位化方程为:
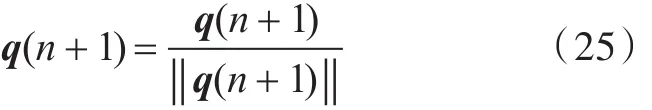
4)令n=n+1,返回至第2)步,直到算完整个仿真时间段。
下面以美国REMUS100小型水下航行体为例进行仿真分析,仿真结果分别如图2~图6所示。仿真所需要的水动力参数以及艇参数可参见文献[10]。首先,应实现水下航行体的重力和浮力平衡,并将重心和浮心配置在同一位置。初始条件取:
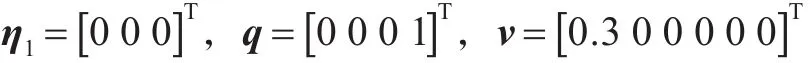
即在水下航行体轴向上有大小为0.3 m/s的初速度。考虑到水下航行体空间的限制,CMG构型为由多个单框架陀螺构成的金字塔型结构[7],其安装角为54.7°,单个陀螺转子转动惯量为Ii=3.25× 10-3kg·m2(i=1,2,3,4)。图2~图4中,单个陀螺转子的角动量为 10(kg·m2)/s,图 5~图 6中,单个陀螺转子的角动量为20(kg·m2)/s。
图2~图4是水下航行体的CMG在Yb轴向上有-0.1 N·m大小的输出力矩(其它方向的输出力矩为0)时所得到的运动曲线图。图2中的曲线呈半圆型,说明水下航行体在垂直面内做回转运动。从图2可以看出水下航行体在水下回转了半圈多,很明显其出现了纵倾角(俯仰角)为-90°的情况。图3给出了四元数随时间的变化曲线,其中ξ2和η的曲线是重合的,均为零。ξ2和η均为零表明潜艇只有纵倾角发生改变,即潜艇只是在垂直面内机动。从图中可以看出曲线光滑,且满足式(12)。图4为利用式(20)将四元数转化成欧拉角(纵倾角)后所得到的曲线,曲线显示水下航行体大约在45 s作用时其纵倾角达到-90°。图2~图4表明,在CMG的作用下,水下航行体在运动过程中出现了纵倾角为-90°的情况,但基于四元数的运动模型仍然能描述水下航行体的运动。
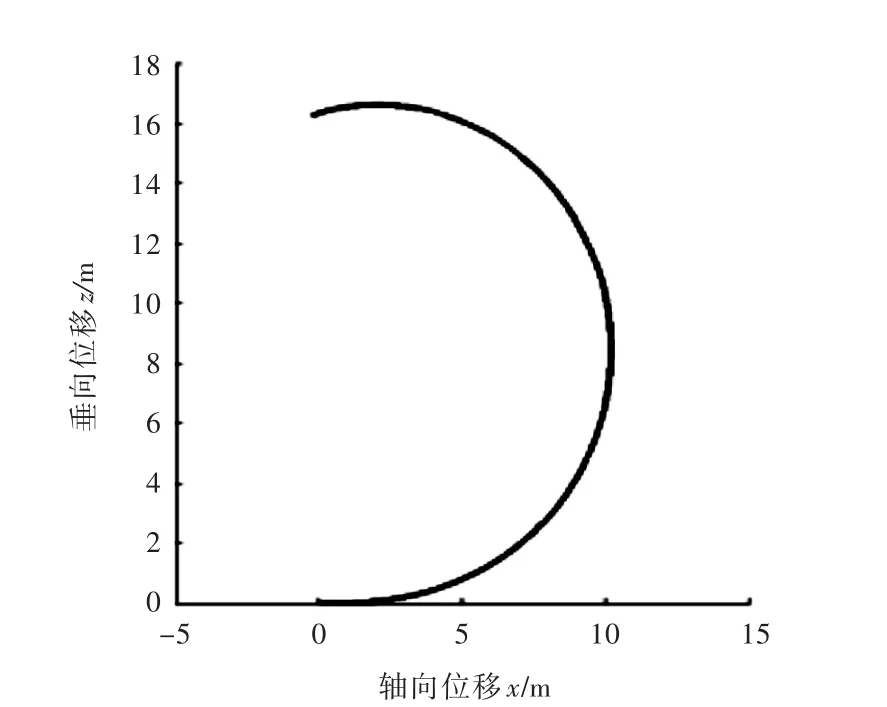
图2 水下航行体垂直面内的运动轨迹Fig.2 Trajectory of an autonomous underwater vehicle in vertical plane
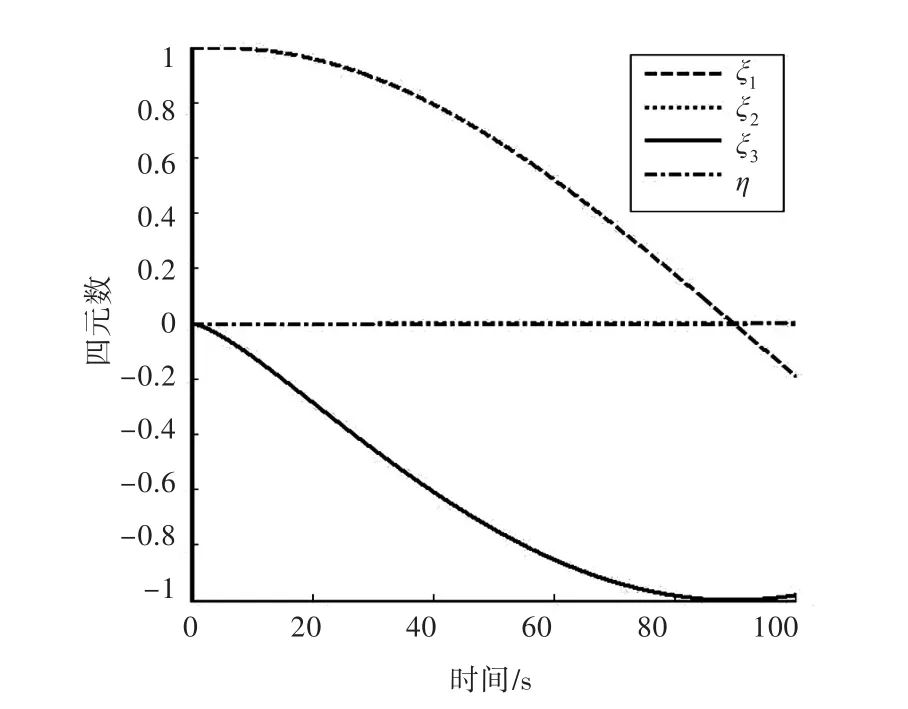
图3 四元数随时间的变化曲线Fig.3 Variation of four-parameter with respect to time
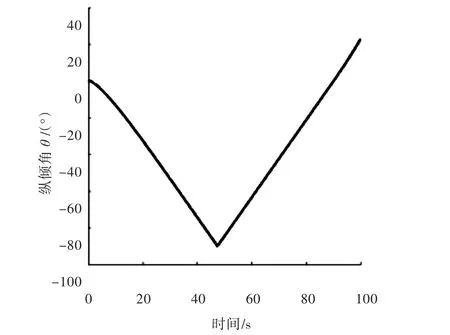
图4 水下航行体纵倾角随时间的变化曲线Fig.4 Variation of pitch angle of an autonomous underwater vehicle with respect to time
图5和图6为给定期望纵倾角θ=-90°,并在PD控制律作用下的水下航行体运动曲线。其中,图5为利用式(20)将四元数转化成欧拉角(纵倾角)后所得到的曲线。可以看出,水下航行体的纵倾角无超调的达到期望角度,最后稳定在-90°。图6则描述了这一运动过程中,水下航行体在垂直面内的运动轨迹,曲线大约在5.2 m左右开始与x轴垂直,说明此位置水下航行体的纵倾角达到-90°,水下航行体垂直于水面,开始往更深水域驶去。图5~图6说明,针对基于四元数的运动模型,可以设计控制器,从而将水下航行体纵倾角控制在-90°。

图5 期望纵倾角θ为90°时,实际纵倾角随时间的变化曲线Fig.5 Variation of pitch angle with respect to time,when the expected pitch angle is 90°

图6 期望纵倾角θ为90°时,水下航行体在垂直面内的运动轨迹Fig.6 Trajectory of an autonomous underwater vehicle in vertical plane,when the expected pitch angle is 90°
4 结 语
本文针对一类纵倾角可能会出现±90°的水下航行体,利用四元数来建立其运动学方程,并运用四元数来代替动力学方程中的欧拉角项。随后,给出了欧拉角和四元数之间的关系,以便于两者之间的相互转换,同时对相关的计算机仿真方法作了说明。最后,给出了计算机的仿真结果。结果表明:当纵倾角出现-90°时(+90°一样),该模型仍然能用于描述水下航行体的运动,并且可以通过设置控制器将其纵倾角控制在-90°。本文所建立的模型能够避免运用欧拉角方法建立的模型所产生的奇异问题,因而适用于水下航行体任意角机动,从而为CMG在水下航行体中的应用奠定了基础。
[1]FOSSEN T I.Guidance and control of ocean vehicles[M].England:John Wiley&Sons Lid Baffins Lane,1994.
[2]黄华红,杨云川,吕艳慧.一种鱼雷俯仰角出现±90°时的姿态仿真方法[J].鱼雷技术,2012,20(3):225-230.
HUANG Huahong,YANG Yunchuan,LV Yanhui.At⁃titude simulation method for torpedo pitch angle at±90°[J].Torpedo Technology,2012,20(3):225-230.
[3]潘常军,郭迎清.基于Simulink的高空空投AUV全弹道仿真系统研究[J].计算机工程与应用,2013,49(8):222-226.
PAN Changjun,GUO Yingqing.High altitude airlaunched AUV's complete trajectory simulation system based on Simulink[J].Computer Engineering and Ap⁃plications,2013,49(8):222-226.
[4]THOMTON B,URA T,NOSE Y,et al.Internal actua⁃tion of underwater robots using control moment gyros[C]//Occeans Europe,2005:591-598.
[5]THORNTON B.The development of zeros-G class un⁃derwater robots:unrestricted attitude control using con⁃trol moment gyros[D].Southampton:University of Southampton,2006.
[6]ROSER X,SGHEDONI M.Control moment gyroscopes(CMGs)and their application in future scientific mis⁃sions[C]//Proc of 3rdESA International Conference.Noordwijk,1997:523-528.
[7]张锦江.单框架控制力矩陀螺系统的构型分析和对比研究[J].中国空间科学技术,2003,23(3):52-56.
ZHANG Jinjiang.Research on configuration analysis and comparison of SGCMG system[J].Chinese Space Science and Technology,2003,23(3):52-56.
[8]TAYLOR J R.Classical mechanics[M].United States of America:University Science Books,2006.
[9]刘暾,赵钧.空间飞行器动力学[M].哈尔滨:哈尔滨工业大学出版社,2003.
[10]PRESTERO T J.Verification of a six degree of free⁃dom simulation model for the REMUS autonomous un⁃derwater vehicle[D].California:Massachusetts Insti⁃tute of Technology,2001.
Applying the Four-Parameter Approach to Establish the Motion Model of an AUV
XU Zhengwu1,TANG Guoyuan1,DENG Zhiyong2,HUANG Daomin3,HUANG Yongzhong1
1 School of Naval Architecture and Ocean Engineering,Huazhong University of Science and Technology,Wuhan 430074,China 2 Wuhan Second Ship Design and Research Institute,Wuhan 430064,China 3 Department of Electronic Warfare,Air Force Early-Warning Academy,Wuhan 430019,China
This paper focuses on a particular type of Autonomous Underwater Vehicle(AUV)that uses the Control Moment Gyros(CMGs)for attitude control.It is noticed that the AUV may have a large attitude angle,and as a result,a proper motion model must be established to avoid the attitude description matrix singularity.To do so,the four-parameter approach is applied to establish the kinematics equation,and the relationship between four-parameter and Euler's angle is then given.When constructing the dynamics equation,the AUV is regarded as a multi-rigid-body system consisting of the AUV itself and CMGs,while Euler's angle is replaced by four-parameter.For validation,the motion model is simulated by the Runge-Kutta method.The results show that the model effectively avoids the singularity.
four-parameter;Control Moment Gyro(CMG);Autonomous Underwater Vehicle(AUV);motion model
U674.76
A
1673-3185(2014)02-12-05
10.3969/j.issn.1673-3185.2014.02.003
http://www.cnki.net/kcms/doi/10.3969/j.issn.1673-3185.2014.02.003.html
期刊网址:www.ship-research.com
2013-08-20 网络出版时间:2014-3-31 16:32
湖北省自然科学基金资助项目(2013CFB154)
徐正武(1987-),男,硕士生。研究方向:舰船与水下航行体运动控制。E-mail:137198217@qq.com
唐国元(1973-),男,博士,副教授,硕士生导师。研究方向:舰船与水下航行体运动控制,舰船机电控制系统及特种装置系统
唐国元
book=29,ebook=259
[责任编辑:饶亦楠]
