航天密封舱设备安装精度仿真分析方法

马俊太 朱光辰 郝平

(中国空间技术研究院载人航天总体部, 北京 100094)

航天密封舱设备安装精度仿真分析方法

马俊太 朱光辰 郝平

(中国空间技术研究院载人航天总体部, 北京 100094)

针对航天密封舱设备安装精度受密封舱内压影响却没有实用的理论预示方法，提出了仿真分析设备安装精度的方法。该方法根据有限元结构仿真分析得到的位移，导出设备的安装精度；另外，提出了精测数据的分析方法，使设备的安装精度变化规律更明显，更容易看出设备旋转的旋转轴、旋转方向、旋转角度，也使精测数据与仿真数据的对比更容易，可为验证仿真分析的准确性提供前提条件。利用一个算例对文章提出的仿真分析方法进行了验证。结果表明，仿真分析方法能准确地确定设备安装角度变化的旋转轴和旋转方向，计算出的旋转角度值与精测结果也基本一致。

航天密封舱设备；安装精度；有限元方法

1 引言

密封舱体是载人航天器主结构，航天器对安装在密封舱体结构上的姿态测量敏感器、交会对接测量敏感器等仪器设备有较高的位置精度要求。航天器在轨工作时，密封舱处于承受内压的环境中，为保证安装精度，航天器部分总装精度测量工作是在密封舱充压条件下完成的。但随着航天器的尺寸越来越大，充压精测使得精测过程过于繁琐，增加了精测的成本和周期。为此，可采用仿真分析方法，预示给出充压对设备安装精度的影响，从而实现不充压精测，简化精测流程。

目前，应用仿真方法研究设备安装精度的文献较少。文献[1]在重力载荷下仿真验证了水平、垂直相结合精测的优势，不过，没有给出具体的分析方法，且方法的计算精度没有得到验证。本文提出了密封舱在内压载荷下分析设备安装精度的具体方法，并根据精测结果对计算结果进行了验证。

设备安装精度包括设备的安装位置和安装角度，在工作中常遇到的是设备的安装角度精度问题，因此本文以下主要讨论设备的安装角度变化问题。

2 仿真方法的建立

本文讨论的密封舱及安装的设备如图1所示，仿真方法中采用的坐标系如下。

图1 舱体及设备示意

(1)密封舱结构坐标系：原点Oj设置在密封舱后端框端面中心，Xj轴沿舱体轴向，指向舱体交会对接机构一端，Yj轴指向Ⅲ象限线,Zj轴指向Ⅳ象限线，如图2所示。

(2)密封舱交会对接面坐标系：原点Oh设置在交会对接机构端面中心，Xh轴沿舱体轴向，指向舱体交会对接机构一端，Yh轴指向Ⅲ象限线，Zh轴指向Ⅳ象限线，如图2所示。为使坐标系的表示更加清晰，图2中将交会对接机构沿Xh轴平移一段距离，与舱体分开。

(3)默认坐标系：为有限元仿真软件中默认的坐标系，软件中所有参数(如节点的位移、坐标等)均在此坐标系中度量，在建模时，常常使其与密封舱结构坐标系重合。默认坐标系原点用O″表示，坐标轴用X″，Y″，Z″表示。

(4)设备坐标系：设备坐标系分为两种，即静设备坐标系和动设备坐标系，如图3所示。静设备坐标系在充压前设定，其位置一旦确定，不随设备位置变化而变化。动坐标系固结在设备上，充压前与静设备坐标系完全重合，充压后因随设备位置变化而发生变化，不再与静坐标系重合。充压前，静设备坐标系(OXYZ)和动设备坐标系(O′X′Y′Z′)各轴的指向因设备的不同而不同。静设备坐标系X，Y，Z轴的端点分别用A，B，C表示，动设备坐标系X′，Y′，Z′轴的端点分别用A′，B′，C′表示。

图2 密封舱上的坐标系

图3 设备坐标系

2.1密封舱结构仿真模型的建立

结构仿真模型的精确性主要取决于：①结构力学特性的精确模拟；②准确的载荷条件；③边界条件的准确模拟；④有限元模型的修正。

密封舱结构主要由蒙皮、桁条、隔框等结构件组成，常用壳、梁等单元进行模拟；舱体在轨时，内压在一定范围内波动，并不是一个特定的数值，所以要准确地确定载荷条件；密封舱在地面总装时，舱体要放置在各种各样的工装结构上，工装的形式确定了一定的边界条件，一般情况下，边界条件对运算结果的影响较大，需要准确的确定；有限元模型初步建立后，为保证模型的精确性，还应对其进行修正。文献[2]提出了一种应用静力响应面方法的有限元模型修正。其主要思路是：确定目标参数与可变参数的模型函数(显式多项式)；在获得模型函数后进行优化计算，确定合理的可变参数数值，使目标参数与试验结果最接近。将有限元模型按照上述得到的可变参数数值进行修正，便可得到较准确的有限元模型。此方法物理意义明确，且易于实现。

2.2由仿真结果导出设备的安装精度

度量设备安装精度的变化，是通过计算充压后动设备坐标系和静设备坐标系的相对位置关系来实现。有限元仿真结果可得到的是位移，无法直接得出坐标系的相对位置关系，因此要进行转换。

(1)将充压后动设备坐标系3个轴的端点和原点的位移从默认坐标系转换到静设备坐标系中。大部分静设备坐标系与默认坐标系重合，不需要转换。不过，也有一部分静设备坐标系要由默认坐标系绕某轴旋转一定角度后得到，此时要进行坐标转换。设静设备坐标系由默认坐标系绕X轴旋转α得到，则有

(1)

式中：x，y，z为静设备坐标系坐标轴的单位向量；x″，y″，z″为默认坐标系坐标轴的单位向量。

(2)

将式(1)代入式(2)，得

(3)

所以

(4)

依照式(4)，可将点的位移转换到静设备坐标系中[3]。

(2)将充压后动设备坐标系坐标轴上3个端点A′，B′，C′的位移减去坐标原点O′的位移，得到只考虑动设备坐标系坐标轴绕静设备坐标系各轴转动引起的坐标轴端点位移。

图4 坐标系旋转示意图

上述夹角θ的计算公式只适用于小于90°的情形，如果θ大于90°，就无法准确定义设备的转向。为此，对计算公式改写如下。

(5)

式中：d为坐标系旋转后C′点在静设备坐标系Y轴上的坐标。

如果C′在Y轴上的坐标d为正，则将d代入式(5)得

(6)

所以，θ<90°。

如果C′点在Y轴上的坐标d为负，则将d代入式(5)得

(7)

所以，θ>90°。

根据上述相同的计算步骤，可以分别求出充压后静设备坐标系坐标轴与动设备坐标系坐标轴之间的9个夹角，组成一个3×3的夹角矩阵如下。

其中：θ11为充压后动设备坐标系X′轴与静设备坐标系X轴的夹角；θ12为充压后动设备坐标系X′轴与静设备坐标系Y轴的夹角；θ21充压后动设备坐标系Y′轴与静设备坐标系X轴的夹角；以此类推。

将充压后的夹角矩阵与充压前的夹角矩阵相减，即可得到夹角变化矩阵。由于充压前动设备坐标系与静设备坐标系重合，依据夹角矩阵的定义，则充压前夹角矩阵如下。

上述计算可以应用编程的方法实现，通过一定的算法即可得到设备的夹角变化矩阵。

2.3仿真结果精确性的验证

通过仿真结果得到充压前后动设备坐标系与静设备坐标系的夹角变化矩阵，为方便与精测数据比较，将精测数据进行转换，得到充压前后动设备坐标系与静设备坐标系的夹角变化矩阵。精测结果提供的是充压前后动设备坐标系与交会对接面坐标系的相对位置关系，难以看出充压前后设备安装角度的变化规律。其解决办法是，消去充压前后动设备坐标系与交会对接面坐标系的相对位置关系，直接分析充压前后动设备坐标系的相对位置关系，即分析充压后动设备坐标系与静设备坐标系的关系。

2.3.1 精测数据的转换

1)计算充压前后动设备坐标系位置的变化

精测数据给出的往往是充压前后动设备坐标系相对交会对接面坐标系的相对位置，须将数据进行转换。

P1=Q1P

(8)

P2=Q2P

(9)

P1=Q1Q2-1P2=Q3P2

(10)

式中：P1为充压后动设备坐标系各轴单位向量组成的矩阵；P2为充压前动设备坐标系各轴单位向量组成的矩阵，与静设备坐标系各轴单位向量组成的矩阵相同；P为交会对接面坐标系各轴单位向量组成的矩阵；P1，P2，P均为3×1矩阵；Q1为P1相对于P的转换矩阵，Q2为P2相对于P的转换矩阵，Q1和Q2可以通过精测数据的夹角矩阵元素求余弦获得[3]，Q3=Q1Q2-1。

对矩阵Q3中各元素取反余弦，得到充压后动设备坐标系和静设备坐标系夹角矩阵K1。

(11)

式中：K为充压前后动设备坐标与静设备坐标系夹角矩阵的变化，即夹角变化矩阵；等号右边第二项的矩阵为充压前动设备坐标系和静设备坐标系的夹角矩阵，充压前动设备坐标系与静设备坐标系重合。

2)判断设备的旋转方向

上述仿真分析结果和精测数据最终都转换成设备坐标系的夹角变化矩阵，因此可用夹角变化矩阵来判断设备的旋转方向。以设备绕静设备坐标系X轴旋转λ角为例(见图5)，X轴方向无变化，旋转后动设备坐标系和静设备坐标系的夹角矩阵见式(12)。

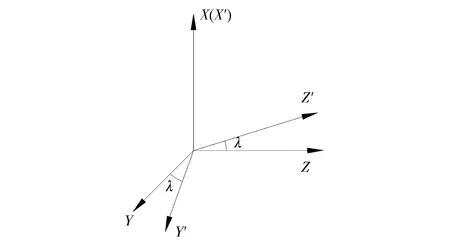
图5 坐标系绕X轴旋转示意

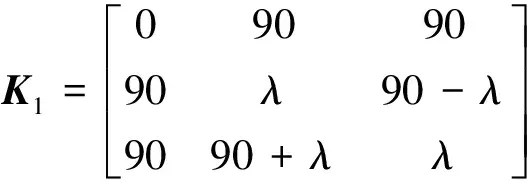
(12)

依照夹角矩阵的定义，K1中第1行第2列位置的元素代表动设备坐标系X′轴与静设备坐标系Y轴的夹角(见图5)，因此应为90°。K1中的其他元素值可进行类似说明。

夹角变化矩阵为

(13)

从K中可以看出，绕X轴旋转时，夹角变化矩阵的第1行和第1列的元素为零。在工程实际中，设备绕X轴旋转时第1行和第1列的元素常常不为零，不过较其他元素要小得多。其余元素的绝对值为绕X轴旋转的角度。同理，可得绕Y轴旋转时第2行和第2列的元素较小，其他元素的绝对值为绕Y轴旋转的角度。绕Z轴旋转时第3行和第3列的元素较小，其他元素的绝对值为绕Z轴旋转的角度。如图5所示，绕X轴正向旋转时，旋转后的Z轴相对于旋转前与Y轴角度变大，表现为夹角变化矩阵的第3行第2列元素为正。可见，旋转方向对矩阵中元素的符号有影响，由此可以判断设备的旋转方向。

2.3.2 仿真结果精确性的确定

精测数据经过上述转换，可以得到设备的旋转轴、旋转方向和旋转角度，与仿真结果进行对比。仿真结果所得旋转轴、旋转方向与精测结果相同，是判断仿真结果精确性的前提。若旋转轴和旋转方向不同，则所得仿真结果无效。在旋转轴和旋转方向相同的情况下，可以根据实测的精度值判断仿真结果的精确性。

3 算例

3.1密封舱结构有限元模型的建立[2,4-5]

分析密封舱充压时结构的变形(位移)，有限元模拟的主要结构有蒙皮、桁条、隔框、仪器板和舱门等。舱内有限桁条有减重孔存在，在有限元建模过程中，由于是桁条用梁单元模拟，无法将减重孔表达出来，本文通过减小桁条的壁厚来等效减重孔的存在，桁条壁厚的等效大小依照应用静力响应面的方法进行修正。

3.2根据仿真结果导出设备的安装角度变化

根据有限元计算结果，得到A′，B′，C′，O′点的位移值，将A′，B′，C′，O′点的位移和坐标数据代入式(1)～式(7)(用编程实现较方便)，即可得到充压前后动设备坐标系的夹角变化矩阵。

经计算得到夹角变化矩阵如下。

其中：矩阵中元素的单位为(′)；第1行第1列的元素表示动设备坐标系X′轴与静设备坐标系X轴在充压前后的夹角变化，第1行第2列的元素表示动设备坐标系X′轴与静设备坐标系Y轴在充压前后的夹角变化，其他以此类推；元素符号为正时表示夹角变大，为负时表示夹角变小。

设矩阵M的第i行第j列元素为mij。当设备绕X，Y，Z轴均有旋转时，m33的绝对值代表绕X轴的旋转角度和绕Y轴的旋转角度的叠加；m22代表绕X轴的旋转角度和绕Z轴的旋转角度的叠加；m11代表绕Y轴的旋转角度和绕Z轴的旋转角度的叠加。m23或m32的绝对值代表绕X轴的旋转角度，取两者的绝对值的平均值作为绕X轴的旋转角度。m31或m13的绝对值代表绕Y轴的旋转角度，取两者的绝对值的平均值作为绕Y轴的旋转角度。m12或m21的绝对值代表绕Z轴的旋转角度，取两者的绝对值的平均值作为绕Z轴的旋转角度。所以，从矩阵M元素的大小分布可以判断，设备绕X轴旋转1.791 4′，绕Y轴旋转3.110 6′，绕Z轴旋转0.090 7′。另外，从矩阵中元素的正负号可以看出，设备绕Y轴负向旋转，绕X轴正向旋转。综上所述，充压后设备绕X轴正向旋转约为1.8′，绕Y轴负向旋转约为3.1′，绕Z轴的旋转角度可以忽略。

3.3仿真分析结果的验证

表1为设备的精测结果，共有6行3列数据，第1行第1列数据是充压后动设备坐标系X′轴与交会对接面坐标系Xh轴的夹角，第1行第2列数据是充压后动设备坐标系X′轴与交会对接面坐标系Yh轴的夹角，单位均为(°)，其他以此类推。

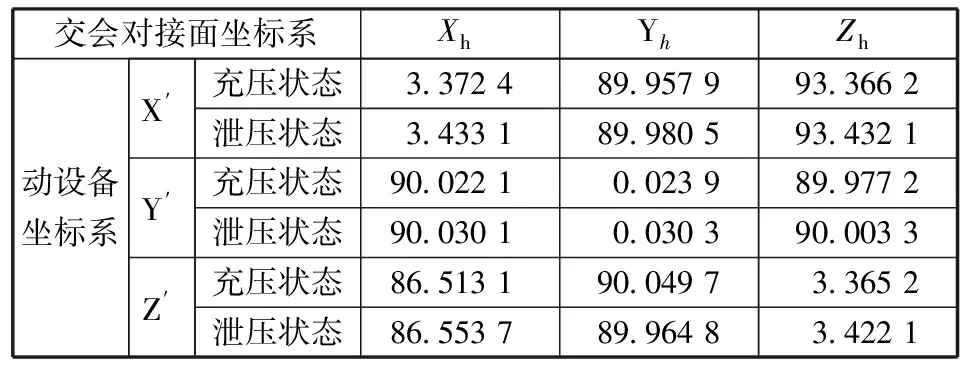
表1 充压前后设备测量数据

依照第2.3.1节中的步骤，计算充压前后动设备坐标系与静设备坐标系的夹角变化矩阵。根据表1数据，充压后，动设备坐标系和交会对接面坐标系的夹角矩阵如下。

由式(10)得Q3。

对Q3中各元素取反余弦，得到充压后动设备坐标系与静设备坐标系的夹角矩阵K1。

充压前后动设备坐标系与静设备坐标系的夹角变化矩阵为K。

依照上述判定方式，由精测数据可得设备绕X轴正向旋转2.028 8′，绕Y轴负向旋转2.121 5′。与仿真结果矩阵M相比，旋转轴和旋转方向都相同，旋转角度误差在30%以内。结果表明，仿真方法能准确反映设备的旋转轴和旋转方向，旋转角度能够在一定范围内反映设备真实精测结果。

4 结束语

本文提出了将仿真结果转换为设备安装角度变化的方法，以及试验精测数据的转换方法，为有限元分析设备安装角度提供了前提条件。实现有限元精确分析设备安装精度，可以简化精测流程。此外，本方法具有一定的通用性，可推广到重力、温度变化等其他载荷因素的分析。

References)

[1]岳荣刚.重力对某型号密封舱精测的影响分析[C]//中国宇航学会返回与再入专业2012年度学术交流研讨会论文集.北京：中国宇航学会，2012：28-33

Yue Ronggang. Influence analysis of gravity on accuracy of equipment assembly[C]//Proceedings of Return and Reentry of Chinese Society of Astronautics 2012 Academical Conference. Beijing: Chinese Society of Astronautics，2012：28-33 (in Chinese)

[2]邓苗毅，任伟新，王复明.基于静力响应面的结构有限元模型修正方法[J].实验力学，2008，23(2)：103-108

Deng Miaoyi, Ren Xinwei, Wang Fuming. Structure finite element model (FEM) updating based on static-load response surface methodology[J].Journal of Experimental Mechanics，2008，23(2)：103-108 (in Chinese)

[3]耿长福.航天器动力学[M].北京：中国科学技术出版社，2006

Geng Changfu. Spacecraft dynamics[M].Beijing: China Science and Technology Press，2006 (in Chinese)

[4]曾攀.有限元分析及应用[M].北京：清华大学出版社，2003

Zeng Pan. Finite element analysis and applications[M].Beijing: Tsinghua University Press,2003 (in Chinese)

[5]龙凯，贾长治，李宝峰，等.Patran2010与Nastran2010有限元分析从入门到精通[M].北京：机械工业出版社，2011

Long Kai，Jia Changzhi,Li Baofeng，et al. Patran2010 and Nastran2010 finite element analysis from rudiment to conversance[M].Beijing: China Machine Press，2011 (in Chinese)

(编辑：夏光)

Simulation Analysis Method of Mounting Accuracy of Space Sealed Cabin Equipments

MA Juntai ZHU Guangchen HAO Ping

(Institute of Manned Space System Engineering, China Academy of Space Technology, Beijing 100094, China)

With considering the lack of practical and theoretical prediction method for influence of space sealed cabin pressure on equipment mounting accuracy, a simulation method is proposed in this paper. The method can transform displacement obtained from finite element structural analysis to equipment mounting accuracy. Besides, this paper puts forward a method to analyze the data of mounting accuracy test which makes the rotation axis, rotation direction and rotation angle more obvious， and the comparison between test data and simulation data easier. This method provides a precondition for verifying the correctness of simulation analysis. The paper puts up an example to validate the simulation analysis method. The result shows that the simulation method can confirm the rotation axis and the rotation direction exactly and the rotation angle is in the same amount level as the test result.

space sealed cabin equipment; mounting accuracy; finite element method

2013-11-07；

：2014-03-06

马俊太，男，硕士研究生，从事航天器总装设计工作。Email：majuntai@126.com。

V465

：ADOI：10.3969/j.issn.1673-8748.2014.03.007