基于肺部组织特征的图像弹性配准研究
2014-07-18瑞周武李衍杰谢耀钦
张 瑞周 武李衍杰谢耀钦
1(中国科学院深圳先进技术研究院 深圳 518055)
2(哈尔滨工业大学深圳研究生院 深圳 518055)
基于肺部组织特征的图像弹性配准研究
张 瑞1,2周 武1李衍杰2谢耀钦1
1(中国科学院深圳先进技术研究院 深圳 518055)
2(哈尔滨工业大学深圳研究生院 深圳 518055)
图像配准是一种建立两幅图像空间对应关系的过程,它被广泛应用于计算机视觉、遥感数据分析及图像处理中,特别是在影像引导放射治疗领域,图像配准发挥着巨大作用。但由于受呼吸运动的影响,精确的肺部影像配准依然是一个充满挑战的难题。目前,尺度不变特征变换(Scale-Invariant Feature Transform,SIFT)已被用于医学图像配准中,并且取得了较理想的结果。然而,SIFT 检测到的仅是图像的块特征,不能有效的反映肺部的运动。文章提出了一种基于 Harris 和 SIFT 算子的杂交型特征检测方法,这种方法能有效检测肺部的组织特征,如血管分叉点和肺部边界等。除此之外,为了有效去除特征匹配过程中产生的错配点,还提出了一种基于互相关和组织结构不变性的滤除错配点方法。文章最后采用一系列不同呼吸周期的肺部 CT 影像来对所提出的算法进行验证。定性和定量的结果表明,该算法较传统的 SIFT 算法更具优越性。
弹性配准;尺度不变特征变换;组织特征;结构不变性
1 引 言
肺癌是全世界范围内造成死亡人数最多的癌症。相关数据显示,全球每年超过 100 万肺癌患者死亡[1]。影像引导放射治疗是一种缓解和治疗肺癌的有效手段,精确的肺部肿瘤定位是影像引导放疗的一个必要步骤[2]。然而由于受呼吸运动的影响,精确的肿瘤定位依然充满挑战。目前,图像配准是肿瘤精确定位的一个关键技术[3],它是一种建立两幅图像空间对应关系的过程,可分为刚性配准和弹性配准两种。然而由于呼吸运动以及周围其他组织的影响,肺部的运动形式并不能使用线性方程描述,因此一般采用弹性配准处理肺部影像。
目前在肺部影像配准常用的方法中,按使用信息的不同可分为基于灰度的配准方法和基于特征的配准方法两种。基于自由表面的配准方法(Freeform Surface Based Registration)[4]、多分辨率的光流场技术( Multi-resolution Optical Flow Technique)[5]、区域狭窄的壳模型(Regional Narrow Shell Model)[6]及 Demons 算法[7]等均为基于灰度信息的弹性配准方法。然而,基于灰度的弹性配准方法面临着两个实际问题:一是由复杂的迭代运算导致的在配准图像间存在较大区域变形时计算复杂度较高的问题;二是只依赖图像灰度导致的对肺部细小结构组织的错配现象。基于特征的配准方法一般用在局域结构信息非常丰富的图像中,并且配准效果与所用匹配点对的准确性有很大关系。尺度不变特征变换 SIFT[8]是一种具有很强鲁棒性的特征提取方法,目前,Xie 等[8]及 Urschler 等[9]使用 SIFT 算法提取胸部 CT 影像特征,并使用薄板样条变换函数(Thin Plate Spline, TPS)对其进行配准,取得了较为理想的结果。然而在使用SIFT 进行特征检测时,对影像进行多尺度处理后得到的特征点只是影像的区域特征,并不能精确地反映影像中的组织特征。
本文提出了一种基于 Harris[11]和 SIFT 的杂交型特征提取方法,这种方法能更有效地检测组织特征,并且检测到的特征大部份分布在感兴趣的组织区域内。同时,我们也提出了一种基于互相关和结构不变性的滤除错配点的方法,这种方法能够将特征匹配过程中产生的错配点有效滤除。本文最后采用了一系列不同呼吸周期的肺部CT 影像来对提出的方法进行测试,实验结果表明以上方法具有明显的优越性。
2 实验方法
本文提出的方法主要包括以下四部分:组织特征检测、特征描述、特征匹配及错配点滤除和薄板样条变换[12]。
2.1 组织特征检测
SIFT 算法在尺度空间中检测到的特征点仅是图像的块特征,并不能真实地反映肺部组织的运动情况。而我们需要的是肺的边界、血管交叉点和肺泡等特征。这些特征一般具有较高的灰度梯度值,因此我们采用 Harris 算法来检测具有高灰度梯度值的特征点。
Harris 检测算子是根据信号的局部自相关函数,测量信号在不同方向上有小位移时信号的变化量[13]。在三维图像中,局部自相关函数定义为:


其中 Ix, Iy, Iz表示在 x,y,z 方向的灰度偏导数。
公式(3)中的矩阵传递的是关于邻域结构的局部强度信息,如果矩阵的 3 个特征值均很大,那么局部自相关函数是一个极值,可选作特征点。在实际实验中,为了提高检测效率,并且在肺部得到均匀分布的特征点,我们选取特征值大于设定阈值且彼此之间大于一定距离的点。
2.2 特征描述
SIFT 特征描述对局部变形及特征检测的微小误差有很强的鲁棒性,被认为是目前最有效的一种特征描述方式[14],因此我们采用 SIFT 算子对每一个检测到的特征点建立描述[15,16]。SIFT 算法使用特征点周围 16×16×16 邻域体素的梯度方向分布,并将其分成 4×4×4 个子区域。每个体素的梯度方向用两个角度表示:方位角 θ 从0°到 360°,俯仰角 φ 从 —90°到 90°。为了建立方向直方图,我们定义每 45°分成一个区间,因此每一个子区域有 8×4 个方向向量来表示本区域的体素梯度。每一个特征共有 2048 维向量对其进行描述,图 1 所示为特征描述结构。
2.3 特征匹配及错配点滤除
为了找到匹配的特征点对,我们将每一个特征的 2048 维方向直方图转化成一个向量,并计算模板图像中一个特征点与目标图像中任意一个特征点的 l2距离。假设 S1和 S2是特征 S 的最佳匹配(l2距 离最小)与次佳匹配点,d1和 d2分别对应S1和 S2与 S 之间的 l2距离,如果比值 r=d1/d2小于一个阈值 τ,那么我们就暂时选择 S1作为特征点 S 的对应匹配点。为提高匹配精度,我们反向重复一次上述过程,选择那些无论从体 V1到V2还是从体 V2到 V1依然匹配的特征点对。然而,经过上述过程找到的匹配特征点中依然存在许多错配点。为了去除这些错配点,我们提出一种根据互相关和组织结构不变性滤除错配点的方法。互相关是两个信号之间相似度的测量函数,它通过式(4)计算得到:

图 1 3D SIFT 描述子图Fig. 1. 3D SIFT descriptor

其中(i, j, k)是在特征点周围一定距离内的体素点位置坐标,A,B 为对应体素的灰度值大小,是距离内体素的灰度平均值。这些灰度值可经过一个高斯窗函数加权标准化处理后得到。如果相关系数 CC 大于一个设定的阈值,则认为两个特征是相似的。
但是,仅使用互相关函数处理后仍有较多错配点残留。在对肺部运动状态的研究中,我们发现肺部组织结构在呼吸运动中的相对位置不会发生很大变化。因此,如果在吸气时某一个特征周围有一定数目的关键点,那么在呼气时,这些关键点依旧会在该特征周围。由此,我们提出基于结构不变性滤除错配点的方法,主要包括以下三个步骤:
(1)模板影像中,在距实验特征点周围最近的点中选取一定数目关键点;
(2)目标影像中,在对应的匹配特征点周围选取相同数目的关键点;
(3)如果这些一定数目的关键点中相互匹配点的个数大于一个给定的阈值,那么就可以确定实验的特征为正确匹配。
这个过程可以用以下伪代码说明:

图 2 展示的是使用上述方法滤除错配点前后的结果。实验所用的匹配特征点对为使用 Harris检测算子所检测到的点,并且使用一个灰度阈值来确保绝大部分检测到的点都能在肺部区域。其中,(a)为使用对称最近邻方法得到的匹配点对;(b)为使用文中提出方法滤除错配点后剩余的特征点对;(c)为使用文中提出方法滤除掉的特征点对。图中红色和蓝色点分别表示在不同肺部影像中检测到的特征点,匹配的特征点对之间用黑线连接。从图中的结果可以看出,上述方法能够有效滤除错配点。
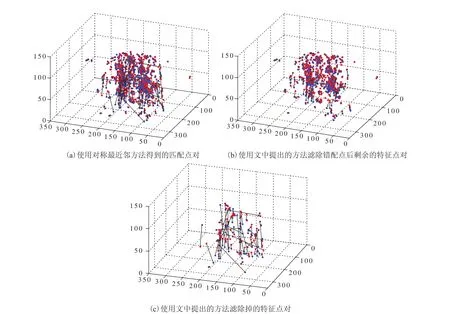
图 2 不同方法滤除错配点结果对比图Fig. 2. Comparison among mismatched pairs removed by different mothods
2.4 薄板样条变换
根据得到的匹配特征点对,我们建立一个变换函数,从而将模板影像变换成目标影像。从数学方面考虑,这存在一个最优化的问题,即如何找到一组变换参数使模板图像能最优地转化成目标图像[17]。
为了找到一个能将模板影像中任意一个体素映射到目标影像中的变换矩阵,我们在本文中选用了薄板样条变换函数。这种方法能够根据控制点对建立起兴趣区域体素与体素之间一一对应的关系。有关 TPS 算法的详细描述可以在Bookstein 的文章[12]中查阅。
3 实验结果与分析
我们选用一系列不同呼吸周期的胸部 CT 影像来对上述方法进行定性和定量的评价。其中,每一个三维影像有 80 层切面,层间距为 2.5 mm,每一个层切面的体素大小为 512×512,体素之间的间距为 0.977 mm。由于各个方向上的体素空间间距不同,我们首先对影像进行各向同性处理,使 x, y, z 方向上的体素之间间距相同。这样处理有以下优势:体素空间各向同性处理可以提高计算效率;层切面中的体素空间间距缩小使整个体数据变小以降低内存消耗;此外,体素空间各向同性可以增加 SIFT 特征描述算子的准确性。实验中所有的图像都在一个奔腾双核 2.8 GHz 主频、3 GB 内存的台式机上进行处理。编程语言为 C++,并且使用了 Insight Segmentation and Registration Toolkit (ITk)[18]函数库。其中部分程序参考了 Xie 等[8]及 Cheung 等[16]的源程序。实验中采用灰度均方差(The Mean of the Square Sum of Intensity Differences,SSD)及图像灰度互相关系数(CC)对最终的配准结果进行定量评价。
图 3 中,(a)为配准之前模板影像与目标影像的融合图像,(b)为使用文中提出的方法配准之后的影像与目标影像的融合图像,为了易于比较,我们将使用传统 SIFT 算法配准后的影像与目标影像的融合图像在(c)中显示。融合图像中的红色区域表示目标影像,绿色区域表示模板影像。从图中可以看出,使用文中提出的方法较传统 SIFT 方法配准后的影像与目标影像之间差别更小,具有明显优势。

图 3 配准前后肺部的融合图像Fig. 3. Fusion images of lung CT images

表 1 上述方法与传统 SIFT 的定量分析Table 1. Comparision of the proposed method and the conventional SIF T
为了定量评价配准效果,表 1 中展示的是使用 SSD 与 CC 的定量评价结果。SSD 越小,说明两幅影像间的差异性越小,配准效果越好;CC越大,说明两幅影像间的相关性越大,配准效果越好。从表 1 可以看出,使用文中提出的方法之后,SSD 从 56727 降到了 37650,CC 从 0.646 升到了 0.740,表明文中提出的方法较传统的 SIFT有更大的优势。
此外,我们请了一位放射物理医师对配准结果选取一些标记点进行评价。实验共随机选取了 15 个点来反映配准结果的平均误差,选取点的试验结果如表 2 所示。表中的坐标误差由目标影像中对应点坐标减去配准影像中对应点坐标得到。在使用传统 SIFT 方法时,这 15 个点在 x、y、z 三个方向上的平均绝对值误差(Mean Absolute Deviation,MAD)为 1.6 mm、1.9 mm 和2.8 mm,而使用我们提出的杂交型方法后降为0.6 mm、0.7 mm 和 0.7 mm。这 15 个点在 x、y、z 三个方向上的标准偏差(Standard Deviation,Std Dev)在使用杂交型方法后从 2.6 mm、2.2 mm、5.2 mm 分别降为 0.9 mm、1.0 mm 和 1.2 mm。实验结果表明,在肺部影像配准中,提出的杂交型方法较传统的 SIFT 方法具有更高的准确度。
一般来说,使用 TPS 算法配准的结果与控制点的数目和位置有很大关系。在实验中,由于我们采用的是根据灰度阈值而不是真实的分割处理,因此使用 SIFT 算法检测到的特征点分布在整个影像体中,而只有一小部分在肺部。而使用我们提出的方法检测到的点则绝大部分都在肺部。以上两种方法均得到了 500 个左右匹配的特征点对 (SIFT:539 对,杂交方法:490 对)。尽管使用杂交型方法得到的正确匹配点对较传统的 SIFT方法略少,但分布在肺部区域的检测点却明显比SIFT 方法在统计上多,能更好地反映肺部的形变特征。图 4 显示为使用上述两种方法检测到的特征点,其中白色的点表示检测到的特征点。

表 2 杂交型方法与传统 SIFT 方法的人工选取标记点的评价结果Table 2. Errors of 15 representative points using the proposed method and conventional SIFT

图 4 不同算法检测到的特征点图Fig. 4. Feature point detection
4 总 结
图像配准是先进的影像引导治疗的基础,对现代医学放射治疗的成功起着关键作用。本文提出了一种杂交型的基于特征的弹性配准方法,该方法首先使用 Harris 进行特征提取,然后利用SIFT 建立起稳定的特征描述,能有效检测组织结构特征。临床肺部 CT 影像数据的实验结果验证了该方法的优越性。此外,文中提出了一种基于互相关和组织结构不变性的匹配点验证方法,该方法具有较强的鲁棒性,能够确保匹配点对的正确性,可以作为传统基于特征配准算法的有效补充手段。
[1] Ferlay J, Shin HR, Bray F, et al. Estimates of worldwide burden of cancer in 2008: GLOBOCAN 2008 [J]. International Journal of Cancer, 2010, 127(12): 2893-2917.
[2] Han X. Feature-constrained nonlinear registration of lung CT images [C] // Grand Changes in Medical Image Analysis: Evaluation of Methods for Pulmonary Image Registration, 2010: 63-572.
[3] Lei X, Brain T, Eduard S, et al. Overview of imageguided radiation therapy [J]. Medical Dosimetry, 2006, 31(2): 91-112.
[4] Lu W, Olivera GH, Chen Q, et al. Automatic recontouring in 4D radiotherapy [J]. Physics in Medicine and Biology, 2006, 51(5): 1077-1099.
[5] Zhang GG, Huang TC, Guerrero T, et al. The use of 3D optical flow method in mapping of 3D anatomical structure and tumor contours across 4D CT data [J]. Journal of Applied Clinical Medical Physics, 2008, 9(1): 59-69.
[6] Chao M, Li T, Schreibmann E, et al. Automated contour mapping with a regional deformable model [J]. International Journal of Radiation Oncology, Biology, Physics, 2008, 70(2): 599-608.
[7] Wang H, Dong L, O’Daniel J, et al. Validation ofan accelerated ‘Demons’ algorithm for deformable image registration in radiation therapy [J]. Physics in Medicine and Biology, 2005, 50(12): 2887-2905.
[8] Xie YQ, Chao M, Xing L. Tissue feature-based and segmented deformable image registration for improved modeling of shear movement of lungs [J]. International Journal of Radiation Oncology, Biology, Physics, 2009, 74(4): 1256-1265.
[9] Urschler M, Bauer J, Ditt H, et al. SIFT and shape context for feature-based nonlinear registration of thoracic CT images [C] // Proceedings of the 2nd ECCV International Conference on Computer Vision Approaches to Medical Image Analysis, 2006: 73-84.
[10] Lowe DG. Distinctive image features from scaleinvariant keypoints [J]. International Journal of Computer Vision, 2004, 60(2): 91-110.
[11] Harris C, Stephens M. A combined corner and edge detector [C] // Proceedings of the 4th Alvey Vision Conference, 1988: 147-151.
[12] Bookstein FL. Principal warps: thin-plate splines and the decomposition of deformations [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(6): 567-585.
[13] Sipiran I, Bustos B. Harris 3D: a robust extension of the Harris operator for interest point detection on 3D meshes [J]. The Visual Computer, 2011, 27(11): 963-976.
[14] Mikolajczyk K, Schmid C. A performance evaluation of local descriptors [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(10): 1615-1630.
[15] Scovanner P, Ali S, Shah M. A 3-dimensional sift descriptor and its application to action recognition [C] // Proceedings of the 15th International Conference on Multimedia, 2007: 357-360.
[16] Cheung W, Hamarneh G. n-SIFT: n-dimensional scale invariant feature transform [J]. IEEE Transactions on Image Processing, 2009, 18(9): 2012-2021.
[17] Xie YQ, Chao M, Xiong G. Deformable image registration of liver with consideration of lung sliding motion [J]. Medical Physics, 2011, 38(10): 5351-5362.
[18] Ibanez L, Schroeder W. The ITK Software Guide [M]. New York: Kitware Incorporation, 2003.
A Study on the Deformable Image Registration Based on the Tissue Features of Lungs
ZHANG Rui1,2ZHOU Wu1LI Yanjie2XIE Yaoqin1
1( Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China )
2( Harbin Institute of Technology Shenzhen Graduate School, Shenzhen 518055, China )
The image registration is a process of establishing spatial correspondences between two images. It is widely used in the computer vision, the remote sensing data analysis and the image processing. Especially in the image-guided radiation therapy, the image registration plays an important role. Recently, the scale-invariant feature transform (SIFT) has been used in the medical image registration, and obtained promising results. However, SIFT is apt to detect blob features which cannot reflect properly motions of lungs. In this paper, a hybrid feature detection method, which can detect lung tissue features effectively based on Harris and SIFT algorithms, was proposed. In addition, a novel method which can remove mismatched landmarks was also proposed. A series of thoracic CT images were tested by using the proposed algorithm. The quantitative and qualitative evaluations show that our method is much better than the conventional SIFT method especially in the case of large deformations of lungs during the respiration.
elastic image registration; scale-invariant feature transformation; tissue features; structure invariance
TP 391
A
2013-11-20
张瑞,硕士研究生,研究方向为模式识别与智能系统、图像处理和医学影像配准;周武,博士后,研究方向为图像分析和配准;李衍杰,副教授,研究方向为随机决策与优化、离散事件动态系统、强化学习和复杂系统控制与优化等;谢耀钦(通讯作者),研究员,博士生导师,研究方向为图像引导放射治疗和医学影像处理和分析和医学物理等,E-mail:yq.xie@siat.ac.cn。
