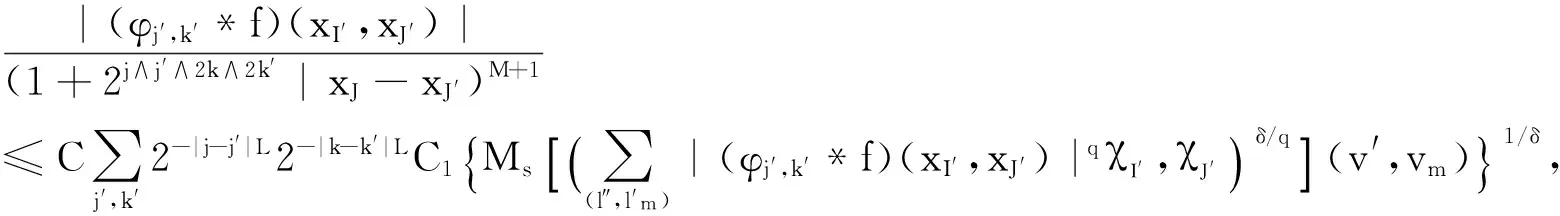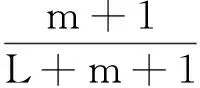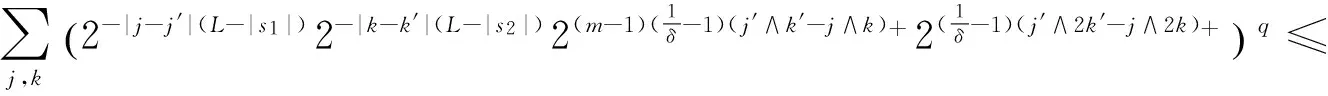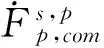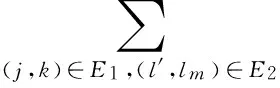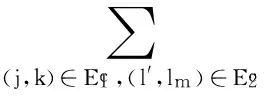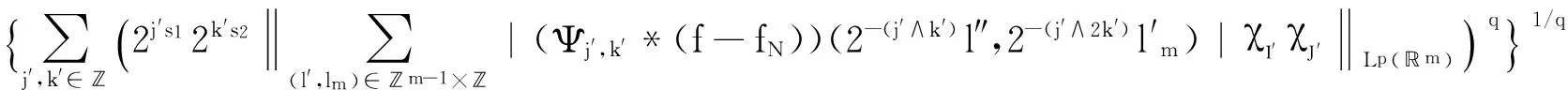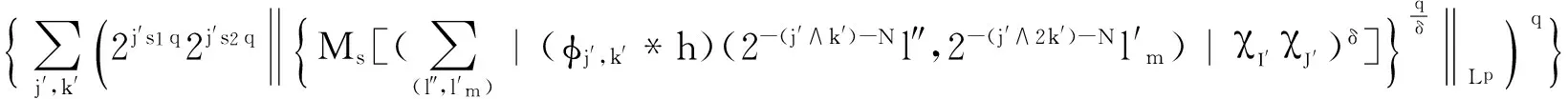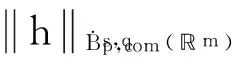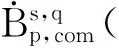Triebel-Lizorkin Spaces and Besov Spaces Associated with Different Homogeneities and Boundedness of Composition Operators
2014-07-18WangHongbin
Wang Hongbin
(Department of Mathematical and Physical Science, Zibo Normal College, Zibo 255130, China)
Triebel-Lizorkin Spaces and Besov Spaces Associated with Different Homogeneities and Boundedness of Composition Operators
Wang Hongbin
(Department of Mathematical and Physical Science, Zibo Normal College, Zibo 255130, China)
In this paper, the author introduces new Triebel-Lizorkin spaces and Besov spaces associated with different homogeneities and proves that the composition of two Calderón-Zygmund singular integral operators with different homogeneities is bounded on these new Triebel-Lizorkin spaces and Besov spaces.
Triebel-Lizorkin spaces; Besov spaces; Calderón-Zygmund operators; composition; discrete Calderón’s identity
1 Introduction and statement of main results
Forx=(x′,xn)∈n-1×and δ>0, we consider two kinds of homogeneities onN
δ°e(x′,xn)=(δx′,δxn),
δ°h(x′,xn)=(δx′,δ2xn).
The first are the classical isotropic dilations occurring in the classical Calder n-Zygmund singular integrals, while the second are non-isotropic and related to the heat equations (also Heisenberg groups). Lete(ζ) be a function onnhomogeneous of degree 0 in the isotropic sense and smooth away from the origin. Similarly, suppose thatH(ζ)is a function onnhomogeneous of degree 0 in the non-isotropic sense, and also smooth away from the origin. Then it is well-known that the Fourier multipliersT1defined by(ζ)=e(ζ)(ζ)andT2givenby(ζ)=h(ζ)(ζ) are both bounded onLpfor 1 To state more precisely our main results, we first recall some notions and notations. Forx=(x′,xm)∈m-1×we denote |x|e=(|x′|2+|xm|2)and |x|h=(|x′|2+|xm|.Wealsousenotationsj∧k=min{j,k}andj∨k=max{j,k}.LetΨ(1)∈s(m)with (1.1) (1.3) (1.5) where the convergence of series inL2(m) andS′/P(m) (the space of tempered distributions modulo polynomials) follows from the results in the classical case. See [1] for more details. Now, we give the definition of Triebel-Lizorkin spaces and Besov spaces associated with different homogeneities. Definition 1.1 Let 0 where where Thesingularintegralsconsideredinthispaperaredefinedby Definition 1.2 A locally integrable functionK1onRn{0} is said to be a Calderón- Zygmund kernel associated with the isotropic homogeneity if (1.6) for all |α|≥0 and (1.7) for all 0 We say that an operatorT1is a Calderón-Zygmund singular integral operator associated with the isotropic homogeneity ifT1(f)(x)=p.v.(K1*f)(x), whereK1satisfies conditions of (1.6) and (1.7). (1.8) forall|α|≥0,β≥0and and (1.9) forall0 WesaythatanoperatorT2isaCalderón-Zygmundsingularintegraloperatorassociatedwiththenon-isotropichomogeneityifT2(f)(x)=p.v.(K2*f)(x),whereK2satisfiesconditionsof(1.8)and(1.9). Ourmainresultsarethefollowing Theorem 1.1 LetT1andT2be Calder n-Zygmund singular integral operators with isotropic and non-isotropic homogeneity, respectively. Then for 0 Intheproofofourmainresult,wewillusethefollowinglemmas. ×Ψj,k(x′-2-(j∧k)l′,xm-2-(j∧2k)lm), where the series converges inL2(m),S∞(m),andS′/P(m). Lemma 2.2 (Almost orthogonality estimates[2]) Suppose thatΨj,kandφj′,k′satisfy the same conditions in (1.1)-(1.4). Then for any given integersLandM, there exists a constantC=C(L,M)>0 such that DenotebyMsthestrongmaximaloperatordefinedby wherethesupremumistakenoverallopenrectanglesinmthatcontainthepointx. SimilartotheproofofLemma3.2in[2],wehavethefollowingestimateofthediscreteversionofthemaximalfunction. Lemma 2.3 LetI,I′be dyadic cubes inm-1andJ,J′be dyadic intervals inwith the side lengthsl(I)=2-(j∧k),l(I′)=2-(j′∧k′)andl(J)=2-(J∧2k),l(J′)=22(j′∧2k′), and the left lower corners ofI,I′and the left end points ofJ,J′ are 2-(j∧k)l′,2-(j′∧k′)l″,2-(j∧2k)lmand,respectively.Thenforanyu′,v′∈I,um,vm∈J,any0 whereC1=C2(m-1)(1/δ-1)(j′∧k′-j∧k)+2(1/δ-1)(j′∧2k′-j∧2k)+and (a-b)+=max{a-b,0}. and whereMisafixedlargepositiveintegerdependingonp,qands.Wealsoletφ(2)∈S(m)withsuppφ(2)⊆B(0,1), and ThediscreteCalderón-typeidentityisgivenbythefollowing Lemma 2.4 Letφ(1)andφ(2)satisfy conditions from (2.1) to (2.4) and Let 0 ×(φj,k*h)(2-(j∧k)-Nl′,2-(j∧2k)-Nlm), wheretheseriesconvergesinL2(m),I are dyadic cubes inm-1andJare dyadic intervals inwith side-lengthl(I)=2-(j∧k)-Nandl(J)=2-(j∧2k)-N, and the left lower corners of I and the left end points of J are 2-(j∧k)-Nl′ and 2-(j∧2k)-Nlm, respectively. Moreover, and Proof By taking the Fourier transform, we have that forf∈L2(m), Applying Coifman's decomposition of the identity operator, we obtain ×(φj,k*f)(2-(j∧k)-Nl′, 2-(j∧2k)-Nlm)+RN(f)(x′,xm) ∶=TN(f)(x′,xm)+RN(f)(x′,xm), where wheretheseriesIare dyadic cubes inm-1andJare dyadic intervals inwith side-lengthl(I)=2-(j∧k)-Nandl(J)=2-(j∧2k)-N, and the left lower corners ofIand the left end points ofJare 2-(j∧k)-Nl′ and 2-(j∧2k)-Nlm, respectively. Similar to the proof of Theorem 4.1 in [2], we only need to prove whereCistheconstantindependentoffandN. Thisproves(2.8)andhenceLemma2.4follows. Similarly,toshowTheorem1.2,weneed Lemma 2.5 Let φ(1)and φ(2)satisfy conditions from (2.1) to (2.4) and let 0 ×(φj,k*h)(2-(j∧k)-Nl′,2-(j∧2k)-Nlm), wheretheseriesconvergesinL2,Iare dyadic cubes inm-1andJare dyadic intervals inwith side-lengthl(I)=2-(j∧k)-Nandl(J)2-(j∧2k)-N, and the left lower corners ofIandtheleftendpointsofJare 2-(j∧k)-Nl′ and 2-(j∧2k)-Nlm, respectively. Moreover, and whereCis the constant independent offandN. Theorem 3.1 Let 0 Proof Letf∈S′/P(m). We denotexI=2-(j∧k)l′ ,xJ=2-(j∧2k)lm,xI′=2-(j′∧k′)l″ andxJ′=.DiscreteCaldern'sidentityonS′/P(m)andthealmostorthogonalityestimatesyieldthatfor<δ whereinthelastinequalityweusethefactsthat(j′∧k′-j∧k)+≤|j-j′|(k-k′|,(j′∧2k′-j∧2k)+≤|j-j′|+2|k-k′|andwehavechosenL>max{m(1/δ-1)+|s1|,(m+1)(1/δ-1)+|s2|}sothat Applying Fefferman-Stein's vector-valued strong maximal inequality onLp/δ(lq/δ)yields Bysymmetry,wegettheconverseinequality.HencetheproofofTheorem3.1iscomplete. AsaconsequenceofTheorem3.1, L2(m)∩(m)isdensein(m).Indeed,wehavethefollowing Corollary 3.1 Let 0 E={(j,k,l′,lm)∶|j|≤N,|k|≤N,|l′|≤N,|lm|≤N} and ×Ψj,k(x′-2-(j∧k)l′,xm-2-(j∧2k)lm), whereΨj,kare the same as Lemma 2.1. SinceΨj,k∈S∞(m), we obviously havefN∈S∞(m). Repeating the same proof as in Theorem 3.1, we can conclude that≤C.ToseethatfNtendstofinm),bythediscreteCaldern'sidentityinS′/P(m)inLemma2.1, ×Ψj,k(x′-2-(j∧k)l′,xm-2-(j∧2k)lm), wheretheseriesconvergesinS′/P(m). Therefore, Arguing as in the proof of Theorem 3.1, we derive Repeating the same proof as in Theorem 3.1, we have Corollary 3.2 Let 0 whereφj,k,φj′,k′,handNarethesameasinLemma2.4. SimilartotheproofofTheorem1.7in[2],wehave Theorem 4.1 Let 0 Proof Letf∈S′/P(m). We denotexI=2-(j∧k)l′,xJ=2-(j∧2k)lm,xI′=2-(j′∧k′)l″ andxJ′=. Discrete Calderón's identity onS′/P(m) and the almost orthogonality estimates yield that for<δ |Ψj,k*f(xI,xJ)| When1≤q<∞,applyingHölderinequalityandwhen0 where in the last inequality we use the facts that (j′∧k′-j∧k)+≤|j-j′|+|k-k′|, (j′∧2k′-j∧2k)+≤|j-j′|+2|k-k′|,and we have chosenL>max{m(1/δ-1)+|s1|,(m+1)(1/δ-1)+|s2|} so that TheproofofTheorem4.1iscomplete. AsaconsequenceofTheorem4.1, L2(m)∩(m)isdensein(m). Indeed we have the following Corollary 4.1 Let 0 E1={(j,k)∶|j|≤N,|k|≤N},E2={(l′,lm)∶|l′|≤N,|lm|≤N}, and ×Ψj,k(x′-2-(j∧k)l′,xm-2-(j∧2k)lm) whereΨj,kare the same as Lemma 2.1. SinceΨj,k∈S∞(m), we obviously havefN∈S∞(m). Repeating the same proof as in Theorem 4.1, we conclude that≤C.ToseethatfNtendstofinm),bythediscreteCaldern'sidentityinS′/P(m)inLemma2.1, ×Ψj,k(x′-2-(j∧k)l′,xm-2-(j∧2k)lm) wheretheseriesconvergesinS′/P(m). RepeatingthesameproofofTheorem4.1,wehave Corollary 4.2 Let 0 whereφj,k*φj′,k′handNarethesameasinLemma2.5. [1] M. Frazier and B. Jawerth, A discrete transform and decomposition of distribution, J. Func. Anal. 93 (1990), 34-170. [2] Y. Han, C.-C. Lin, G. Lu, Z. Ruan and E. Sawyer, Hardy spaces associated with different homogeneities and boundedness of composition operators, Rev. Mat. Iberoam. 29 (2013), 1127-1157. [3] D. H. Phong and E. M. Stein, Some further classes of pseudo-differential and singular-integral operators arising in boundary-value problems I, composition of operators, Amer. J. Math. 104 (1982), 141-172. [4] S. Wainger and G. Weiss, Proceedings of Symp. in Pure Math. 35 (1979). [5] X. Wu, Weighted Carleson Measure Spaces Associated with Different Homogeneities, Canad. J. Math.(2013), doi: 10.4153/CJM-2013-02-11. (责任编辑:胡安波) 2014-06-21 王洪彬(1981-),男,山东淄博人,博士,淄博师范高等专科学校数理系教师,主要从事调和分析方向研究。 O174.2 A (2014)04-0049-10 注:本文为淄博师范高等专科学校校级课题“变指标Herz型空间中算子的有界性”[13xk023]的阶段性研究成果。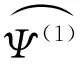
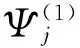
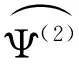
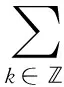
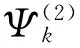
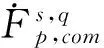
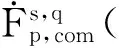
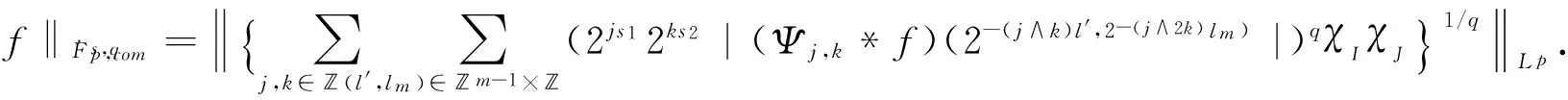
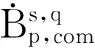

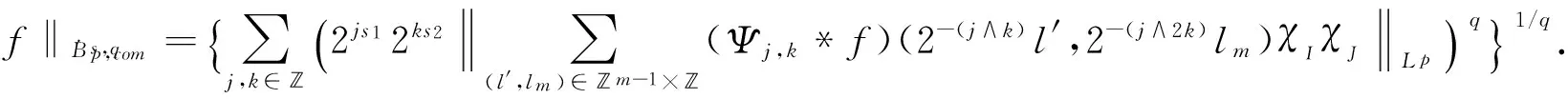

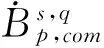
2 Some lemmas
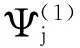

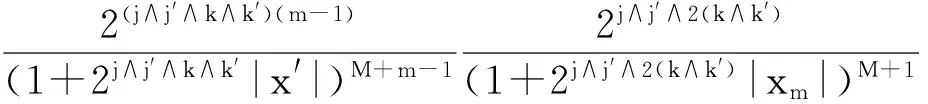
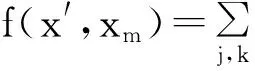

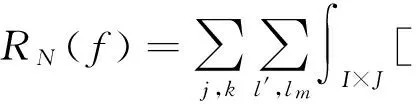
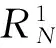
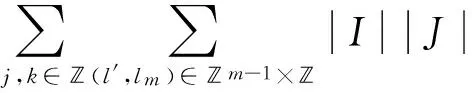
3 Proof of Theorem 1.1
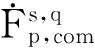
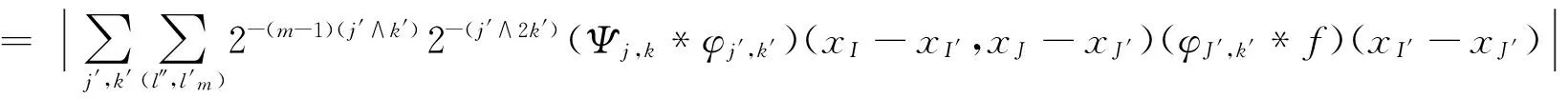
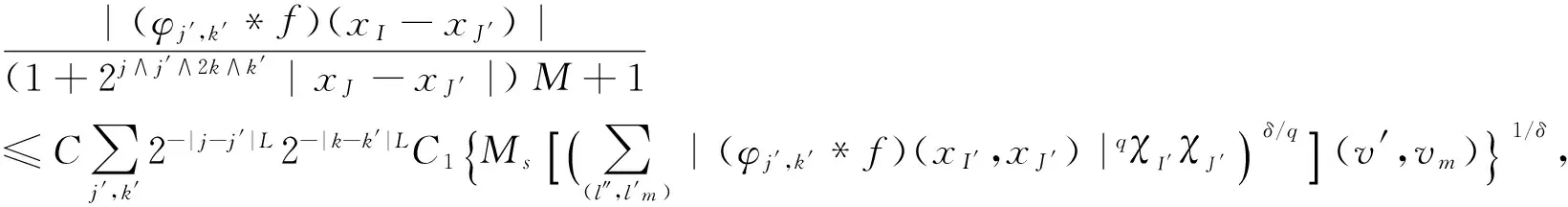
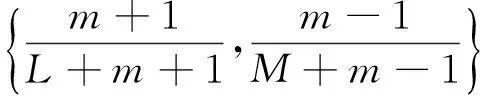
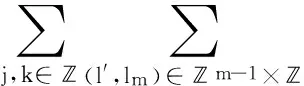
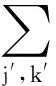
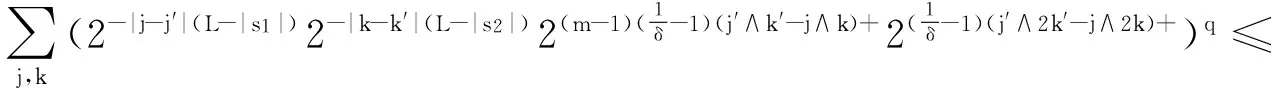
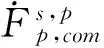
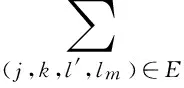
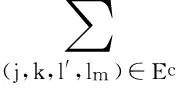
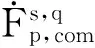
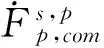
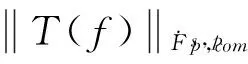

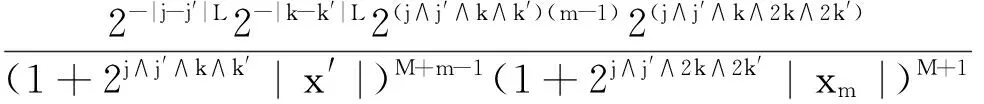
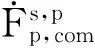
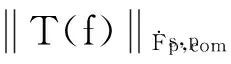
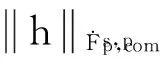
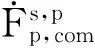
4 Proof of Theorem 1.2