基于iSIGHT集成平台的次镜支撑结构优化设计

王巧霞 郭崇岭

（北京空间机电研究所，北京 100094）

0 引言

次镜支撑结构是空间光学遥感相机中的关键支撑结构，其结构稳定性对成像品质有很大的影响；因结构不稳定引起的次镜在光学系统中的轴间距、俯仰如果有很小的偏离就会对相机的成像品质有很大的影响；次镜支撑结构的稳定性跟材料的选择、结构型式密切相关；同时次镜支撑结构还受到光学系统遮拦比、质量及力学环境因素的限制；为满足光学系统中遮拦比要求，次镜支撑结构的结构型式将受到严格的限制；为满足地面装调以及发射力学环境的要求，次镜支撑结构必须具有较高的刚度和强度；同时，次镜支撑结构应尽量轻量化。综上，为满足对次镜支撑结构各方面的要求，对次镜支撑结构进行分析和优化设计具有重要意义。

虽然目前有限元技术己经广泛应用，针对不同问题的各种优化理论和算法也取得非常大的进展，很多大型有限元分析软件都提供了优化分析模块，但提供的优化算法有限，对于涉及多个目标多变量呈现高度非线性的优化问题显得无能为力。对于多设计变量、多约束及多目标的优化分析，由于涉及到的变量、约束、目标很多，计算量往往会很大，如果设计人员自编程序解决多目标优化问题，不仅给设计人员带来很大困难，还会大大增加工作量，费时费力。本文研究的以 iSIGHT为集成平台的多目标优化设计方法及优化策略可以快速地找到最优方案，大大提高优化效率及产品的可靠性，可应用于其他结构设计乃至整个遥感器的设计中。

1 基于iSIGHT的次镜支撑结构优化策略

某空间遥感相机是一台轻小型高性能全色多光谱光学遥感器，采用了复材筒连接主次镜的结构型式；在次镜支撑结构中，次镜支撑框、前法兰、后法兰为钛合金薄壁结构，前镜筒为壁厚 2mm的格栅筒碳纤维复合材料结构；根据对次镜支撑结构稳定性要求，进行了初始结构设计，并从热稳定性及结构稳定性两个方面确定了多个设计变量及多个优化目标；根据多目标优化的特点设计了基于 iSIGHT的次镜支撑结构优化策略并通过Hypermorphe模块实现了基于iSIGHT的复杂结构的参数化有限元模型的建立。

1.1 次镜支撑结构初始结构设计

目前杆系次镜支撑结构中较成熟的结构型式有3种：A型桁架结构、四翼梁支撑结构及三翼梁支撑结构[1-6]，如图1所示。

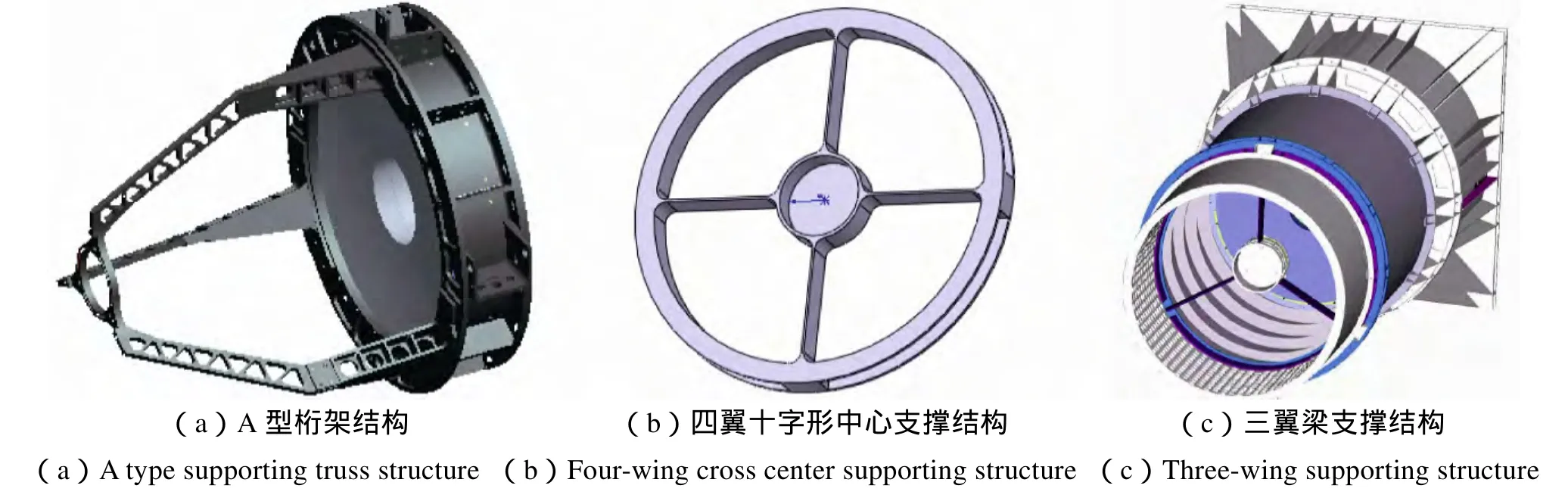
图1 3种较成熟的杆系次镜支撑结构形式Fig.1 Three types of secondary mirror supporting structure

在次镜支撑结构初步设计时，选取了三翼梁支撑结构、三翼与内环相切结构、四翼梁十字形中心支撑结构进行对比分析，并在整机中进行了模态分析。通过分析得出：三翼梁与内环相切结构的一阶频率最高，且为整机模态，说明此结构的刚度最大；同时，三翼与内环相切还有利于机械加工，从而保证加工精度；三翼梁与内环相切的结构还可卸载结构自身因温度变化产生的应力。因此，某空间遥感相机中次镜支撑结构采用三翼与内环相切结构，初步设计模型如图2所示。

1.2 次镜支撑结构优化目标及设计变量选择

根据对次镜支撑结构稳定性要求，从热稳定性及结构稳定性两方面确定了4个优化目标，分别为次镜支撑结构：1）热变形最小；2）X向静力变形最小；3）Z向静力变形最小；4）一阶频率最大。

通过对次镜支撑结构的形状及尺寸进行分析，选取了7个设计变量，各设计变量具体位置如图3所示。

图2 次镜支撑结构示意Fig.2 Schematic diagram of secondary mirror supporting structure

图3 设计变量示意Fig.3 Schematic diagram of design variables

1.3 基于iSIGHT的优化策略

次镜支撑结构涉及4个优化目标，7个优化变量，对于多目标的优化设计，有时需要使多个目标在给定的区域上都能达到最优；然而这些目标一般又是相互冲突的，所以，在解决多目标优化设计问题时，就必须对各性能指标进行综合评定；同时如何选取影响结构性能的主要设计变量，从而简化优化过程、了解各设计变量之间的相互关系及对目标的影响是优化分析的一个非常关键的问题[7-10]。

在基于iSIGHT的次镜支撑结构的优化设计中，设计了通过Hypermesh建立参数化模型，通过Nastran进行分析求解，通过 iSIGHT进行参数驱动及优化评估的优化方法；设计了灵敏度分析—近似模型—优化算法的优化策略。通过灵敏度分析筛选主要设计变量，并通过获取的大量样本点建立近似模型，可以更加清楚的认识设计空间的性质及各个设计变量与目标之间的关系，从而减少仿真分析的次数，提高优化算法性能，最终根据对各个目标的关注程度选择出最优设计方案。

1.4 基于iSIGHT的参数化有限元模型的建立方法

基于iSIGHT平台进行优化分析时需要进行参数驱动，首先在Hypermesh中建立有限元模型，在网格模型上直接操作达到预想的结构形状和尺寸，后台会记录操作的命令流文件；通过在 iSIGHT中读取并修改命令流文件中的有限元参数来建立参数化有限元模型。建立的次镜支撑结构参数化有限元模型如图4所示。

图4 参数化有限元模型示意Fig.4 Schematic diagram of parameterized FEM model

2 基于iSIGHT的优化结果及评估

根据基于iSIHGT设计的次镜支撑结构优化方法及优化策略进行优化分析，经过1 029次迭代计算，得到了各设计变量对目标的灵敏度、设计空间及最优设计方案。

2.1 优化策略分析数据

通过灵敏度分析，各设计变量对目标的灵敏度如图5～6所示（蓝色表明是正影响，红色表明是负影响）。

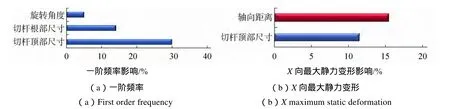
图5 各设计变量对一阶频率、X向最大静力变形的影响Fig.5 Influences of design variables on first order frequency and on X maximum static deformation

图6 各设计变量对Z向最大静力变形、热变形的影响Fig.6 Influences of design variables on Z maximum static deformation and on thermal deformation

通过灵敏度分析（图5～6）可以看出：1）切杆顶部尺寸、切杆根部尺寸对一阶频率有较大的影响；2）轴向距离对X向静力变形有较大影响；3）轴向距离对Z向静力变形有较大的影响；4）旋转角度、切杆顶部尺寸对热变形有较大的影响。

本文选取了700个采样点建立了次镜支撑结构近似模型，分析得出的次镜支撑结构的二维设计空间如图7所示（图中蓝色点表示初始设计点）。三维设计空间如图8所示，即多个设计变量对同一目标的影响趋势。对于多目标的优化设计，多个目标一般不能同时达到最优，必须对各指标进行综合评定。

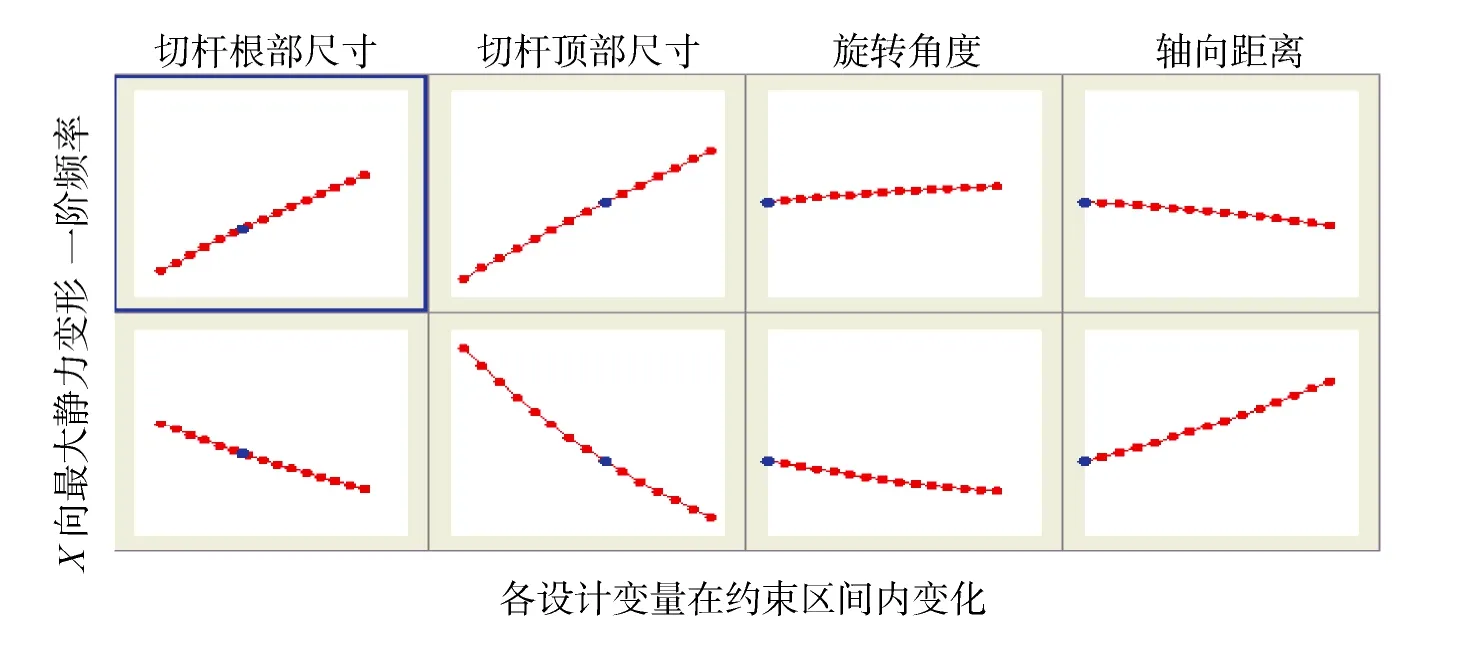
图7 各设计变量在整个设计区间内对目标的影响趋势Fig.7 Influence of design variables on X maximum static deformation and first order frequency

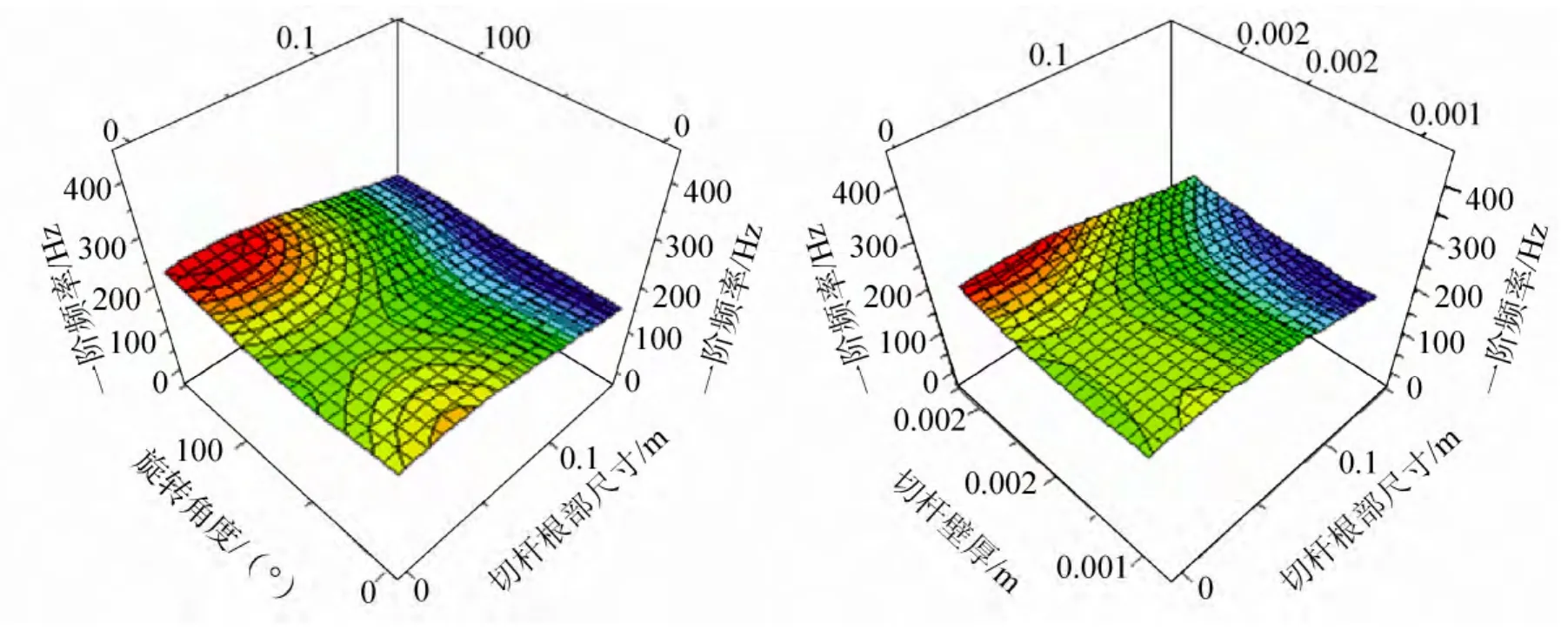
图8 设计变量对一阶频率响应曲面Fig.8 Response surface of design variables on first order frequency

通过图7～8的近似模型分析可以看出：1）改变当前设计值会引起各个目标的变化趋势；2）增大轴向距离变量会增大变形值、降低频率值，因此不应增大其值；3）增加切杆根部、切杆顶部及旋转角度的值，频率升高，静力变形减小；4）通过旋转角度、切杆根部、切杆壁厚尺寸对一阶频率响应曲面图可以看出设计空间呈现多峰性，即在响应面上呈现多个红色峰值区域，因此需要用全局优化算法找到全局最优解。

2.2 优化前后设计变量对比

优化前后各设计变量的对比如表1所示，可以看出优化后切杆根部尺寸及旋转角度的变化较大；与灵敏度分析及设计空间分析趋势吻合。

表1 优化前后各设计变量值对比Tab.1 Design variables comparison before and after optimization

2.3 优化前后次镜支撑结构综合性能对比

对优化前后的次镜支撑结构进行了静力对比分析、热对比分析、模态对比分析及正弦加速度对比分析。

2.3.1 静力对比分析

优化前次镜支撑结构在X向的静力变形及等效应力分别为2.26μm、0.406MPa，优化后为2.25μm、0.404MPa，分别改善0.4%、0.5%；Z向的静力变形及等效应力优化前分别为4.89μm、0.780MPa，优化后为3.61μm、0.678MPa，分别改善26.2%、13.1%。

2.3.2 热分析对比

在次镜部件部位温度为18℃，前法兰、复材筒、后法兰等温度为20℃的情况下，对次镜支撑结构进行了的热分析优化前热变形5.23μm，优化后热变形为5.21μm，改善0.4%；优化前后热应力改善很小，仅0.1%。

2.3.3 模态对比分析

对次镜支撑结构进行模态分析，振型及频率如图9所示（振型均为沿光轴方向平动）。

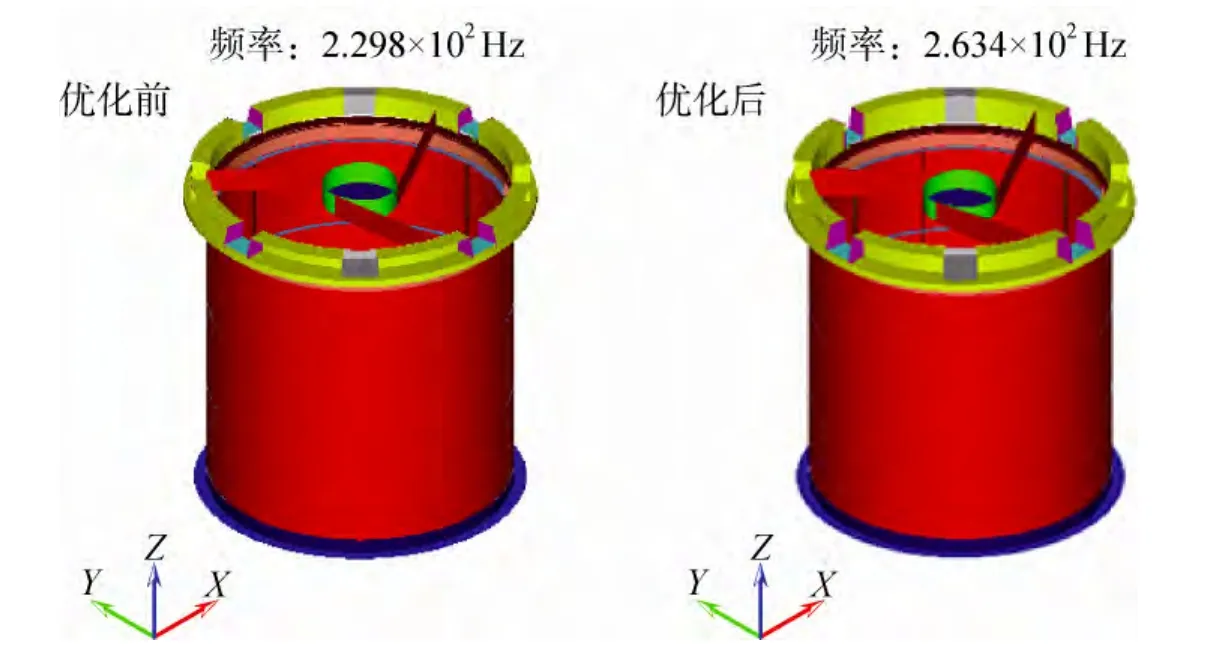
图9 优化前后一阶模态对比Fig.9 First order frequency comparison before and after optimization

图9中优化前一阶频率为229.8Hz，优化后为263.4Hz，提高了33.6Hz，改善了14.6%。

2.3.4 正弦加速度对比分析

在频率10～2 000Hz范围内，在Z向施加1gn的加速度进行光轴方向的正弦响应分析。优化前后次镜部件的响应曲线如图10所示，响应放大倍数由优化前的17倍减小为优化后的16倍，改善5.9%。

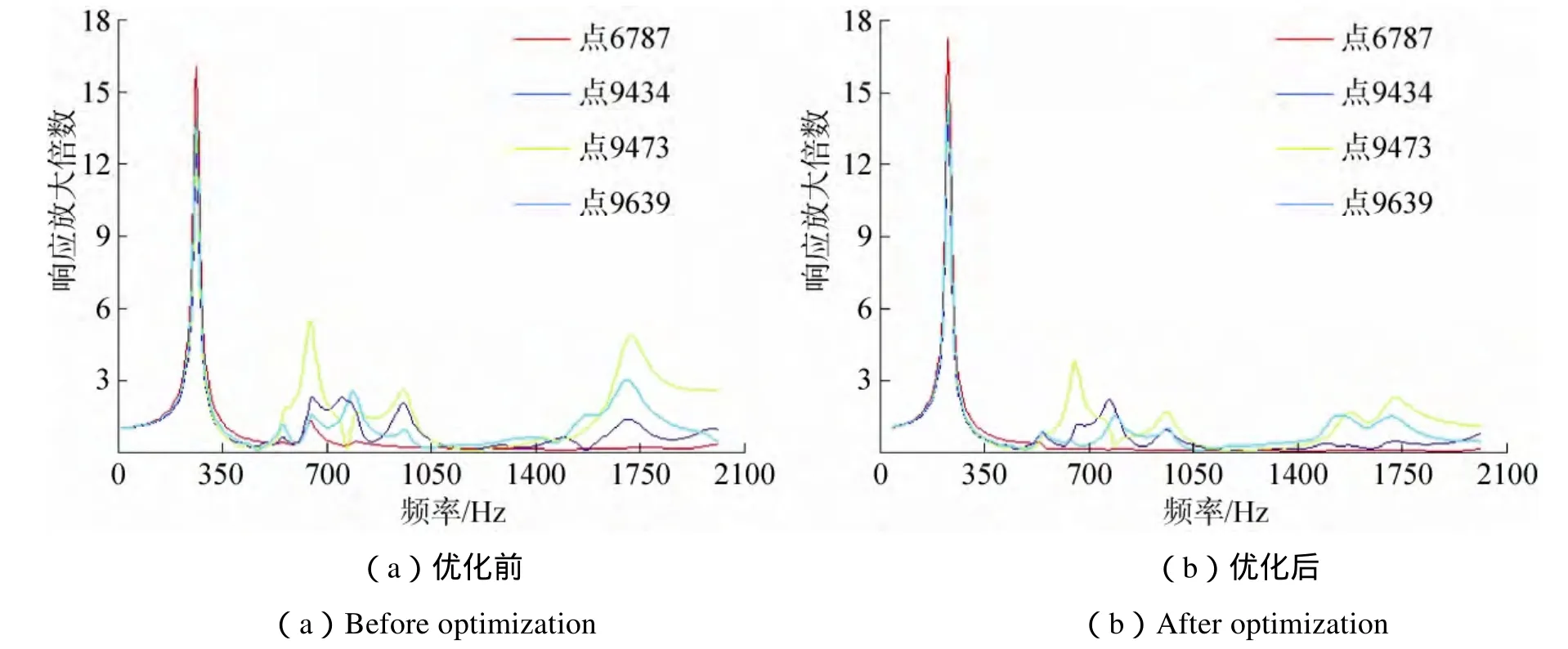
图10 优化前后Z向正弦加速度响应对比Fig.10 Sine acceleration response comparison before and after optimization

2.3.5 综合性能对比

优化前后次镜支撑结构的综合性能对比如表2所示，可以看出优化前后次镜支撑结构的力学性能有了较大的改善，优化后Z向静力变形改善了26.2%，Z向等效应力改善了13.1%，一阶频率改善了14.6%，大大提高了次镜支撑结构的稳定性。

表2 优化前后结果对比Tab.2 Performance contrast before and after optimization

3 结束语

本文通过对某遥感相机次镜支撑结构优化方法的研究，解决了复杂结构多目标、多约束及多设计变量无法自动进行优化设计的难题。以iSIGHT为集成平台、采用Hypermorphe模块实现了复杂结构的参数化有限元模型的建立；提出了多目标、多约束及多设计变量复杂结构的优化策略，即灵敏度分析—近似模型分析—优化设计的优化策略；优化效率大大提高，结构性能大大改善；优化后次镜支撑结构的力学性能得到显著提高。

随着我国空间光学相机的分辨率要求越来越高，光学系统的口径也越来越大，这对光学系统支撑结构的稳定性提出了更高的要求。采用 iSIGHT平台进行软件集成，通过定义多种工况来综合考虑各个设计变量对目标的影响，自动进行优化设计，可以在最短的时间里，探索更多的设计方案；同时，通过多种目标的综合评价、确定优化方向，可以快速地找到最优方案，可以大大提高优化效率及产品的可靠性。这种灵敏度分析—近似模型分析—优化分析的优化思路也可以应用于其他结构设计乃至整个光学遥感器的设计中。

（

）

[1] 王富国, 张景旭, 杨飞, 等.四翼梁式次镜支撑结构的研究[J].光子学报, 2009, 38（3）: 674-676.

WANG Fuguo, ZHANG Jingxu, YANG Fei, et al.Crossed-plate Type Support of the Second Mirror[J].Acta Photonica Sinica,2009, 38（3）: 674-676.（in Chinese）

[2] 梁文科, 刘顺发.次镜支撑结构的力学性能分析[J].仪器仪表学报, 2007, 28（5）: 859-863.

LIANG Wenke, LIU Shunfa.Mechanical Analysis of Secondary Mirror Supporting Structure[J].Chinese Journal of Scientific Instrument, 2007, 28（5）: 859-863.（in Chinese）

[3] 陈荣利, 张禹康.空间高分辨率CCD相机次镜支架最佳结构设计[J].光子学报, 2004, 33（10）: 1151-1154.

CHEN Rongli, ZHANG Yukang.The Optimal Design of Secondary Mirror Bracket of High Resolution CCD Camera[J].Acta Photonica Sinica, 2004, 33（10）: 1151-1154.（in Chinese）

[4] 陈荣利, 樊学武.高分辨率TDICCD相机轻量化技术[J].航天返回与遥感, 2003, 24（2）: 20-24.

CHEN Rongli, FAN Xuewu.Lightweightening Technology for High Resolution TDICCD Camera[J].Spacecraft Recovery &Remote Sensing, 2003, 24（2）: 20-24.（in Chinese）

[5] 张雷, 金光.轻型空间相机桁架结构设计与模态分析[J].空间科学学报, 2008, 28（3）: 260-263.

ZHANG Lei, JIN Guang.Structure Design and Modes Analysis for the Truss of Light High Resolution Space Camera[J].Chinese Journal of Space Science, 2008, 28（3）: 260-263.（in Chinese）

[6] 张林波, 任戈.四翼十字形中心支撑结构的动力学分析[J].光学精密工程, 2003, 11（5）: 472-475.

ZHANG Linbo, REN Ge.Dynamic Analysis for Supporting Structure of Crossed-plate Type[J].Optics and Precision Engineering, 2003, 11（5）: 472-475.（in Chinese）

[7] 李哲, 马忠辉.多学科优化设计在航空航天领域的应用及发展[J].航天返回与遥感, 2004, 25（3）: 65-69.

LI Zhe, MA Zhonghui.Study and Development of Multidisciplinary Design Optimization[J].Spacecraft Recovery & Remote Sensing, 2004, 25（3）: 65-69.（in Chinese）

[8] 任江华.大型工程结构优化设计方法与策略研究[D].北京: 北京交通大学, 2006.

REN Jianghua.Optimization Design Methods and strategies Research for Big Scale Structure[D].Beijing: Beijing Jiaotong University, 2006.（in Chinese）

[9] 夏人伟.工程优化理论与算法[M].北京: 北京航空航天大学出版社, 2003.

XIA Renwei.Engineering Optimization Theory and Algorithm[M].Beijing: Beijing Beihang Press, 2003.（in Chinese）

[10] 孙晨.多学科设计优化方法与技术的应用[D].北京: 北京航空航天大学, 2004.

SUN Chen.Application of Multidisciplinary Design Optimization Method and Technology[D].Beijing: Beihang University,2004.（in Chinese）

[11] 宋保维, 李楠.iSIGHT在多目标优化问题中的应用研究[J].火力与指挥控制, 2008, 33（增刊）: 133-135.

SONG Baowei, LI Nan.Application Research of iSIGHT in Solving Multi-objective Design Optimization Problems[J].Fire Control and Command Control, 2008, 33（Supplement）: 133-135.（in Chinese）

[12] Koch P N, Evans J P, Powell D.Interdigitation for Effective Design Space Exploration Using iSIGHT[J].Journal of Structural and Multidisciplinary Optimization, 2002, 23（2）: 111-126.

[13] Deb K.Multi-objective Optimization Using Evolutionary Algorithms[M].Chichester, UK: Wiley, 2001.

[14] Sobieski J S, Haftka R T.Multidisciplinary Aerospace Design Optimization: Survey of Recent Developments[J].Structural Optimization, 1997, 14（1）: 1-23.

[15] Shinya W, Tomoyuki H.Neighborhood Cultivation Genetic Algorithm for Multi-Objection Optimization Problems[C].SEAL-2002, 2002: 198-202.