群体决策基数表示的一个充要条件
2014-07-16刘冰,刘鹏
刘 冰,刘 鹏
(1.南京工业职业技术学院 文理学院,江苏 南京 210023;2.东南大学 数学系,江苏 南京 210096)
人们研究群体决策问题时,更多的是在序数意义下进行各种情况的讨论,其中偏爱规则(或称多数规则)[1,2]是群体决策中基本的决策规则。文[3]研究了该规则所满足的充分和必要条件;文[4]、[5]研究了较多规则的扩展形式,文[6]、[7]、[8]探讨了不同的集结规则;对于随机情况下,文[9]提出群体随机偏爱规则(映射)及随机偏爱公理,并且建立了相应的不可能性定理;文[10]、[11]和[12]则各给出随机偏爱群体决策的一些选优排序方法。
然而,现实生活中,更多的情况是由评委直接给出被评对象的分数或效用值,这涉及的是群体决策的基数表示形式。文献[13-16]研究了福利经济学中的贫困问题,给出其数值表示形式以及相应的公理。本文借鉴其研究方法,对于供选方案中个体具有多个属性时的基数表示问题,给出一个效用集结函数,证明了该效用集结函数满足文献[14]、[17]、[18]中给出的六个公理,在其中几个公理的组合下,可以证明效用集结函数恰能用我们所给出的形式表示,即为一个充分必要条件。最后我们提出在该效用集结函数下对方案集的群体排序算法。
1 问题表述
对于被评对象具有多个属性时的选优排序问题,我们给出一个框架,并提出一个效用集结函数。
设X={x1,…,xs}(s≥2)是供选方案集,其中xi=(xi1,xi2,…,xin)∈Rn表示第 i组方案的 n 个属性集,G={DM1,…,DMl}是决策群体,其中 DMr(r=1,…,l;l≥2)是第 r个决策个体。
定义 2.1[1]设 ur(xij)∈[0,1](i=1,…,s;j=1,…,n;r=1,…,l)是 DMr关于 xij的效用函数值,Ur是 DMr关于 xi的效用函数,(ur(xi1),ur(xi2),…,ur(xin))(r=1,…,l;i=1,…,s)是效用函数值断面,记Δ是效用函数值断面集,则有Δ={(ur(xi1),ur(xi2),…,ur(xin))|i=1,…,s;r=1,…,l}。
定义 2.2设映射F:Δ→R+
为效用集结函数(其中R+是非负实数)。
下面我们给出F的一种具体表达形式,并进行相关阐述和证明。我们取
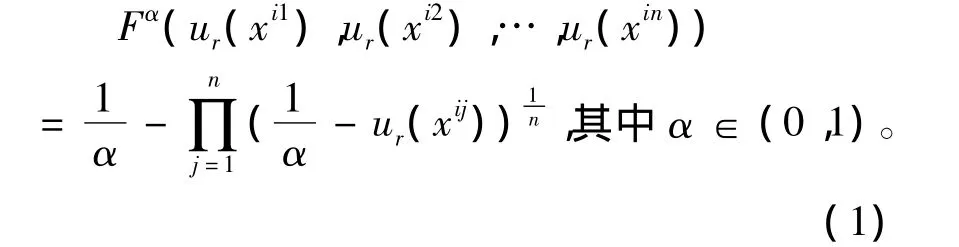
其中当 α =1时,有 F1(ur(xi1),ur(xi2),…,当α→0时,我们有下面引理:
引理1对所有的 U=(ur(xi1),ur(xi2),…,ur(xin))∈Δ 和任意的 α∈(0,1),都有
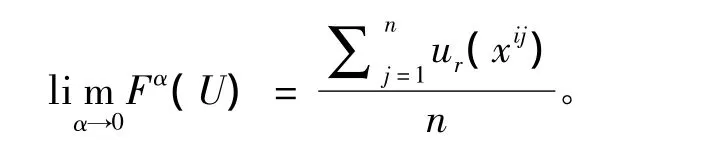

2 基本知识
公理O[14](单调性条件)映射F满足单调性公理,如果对任意的 U =(ur(xi1),ur(xi2),…,ur(xin))∈ Δ 和 U'= (u'r(xi1),u'r(xi2),…,u'r(xin))∈Δ使得∀j,ur(xij)≥u'r(xij),并且∃k,ur(xik)>u'r(xik),那么F(U)>F(U')。
说明:由Fα的构造,易得其满足单调性公理。
公理T[14](传递性公理)映射F满足传递性公理,如果对任意的 U=(ur(xi1),ur(xi2),…,ur(xin))∈Δ 和U'=(u'r(xi1),u'r(xi2),…,u'r(xin))∈Δ使得,ur(xik)=u'r(xik)∀k≠i,jur(xii)≥u'r(xij)并且有u'r(ii)=ur(ii)+ε≤1和u'r(xij)=ur(xij)-ε≥0(ε >0),那么F(U')> F(U)。
引理 2对所有的 U=(ur(xi1),ur(xi2),…,ur(xin))∈Δ和任意的α∈(0,1),都有Fα满足传递性公理。
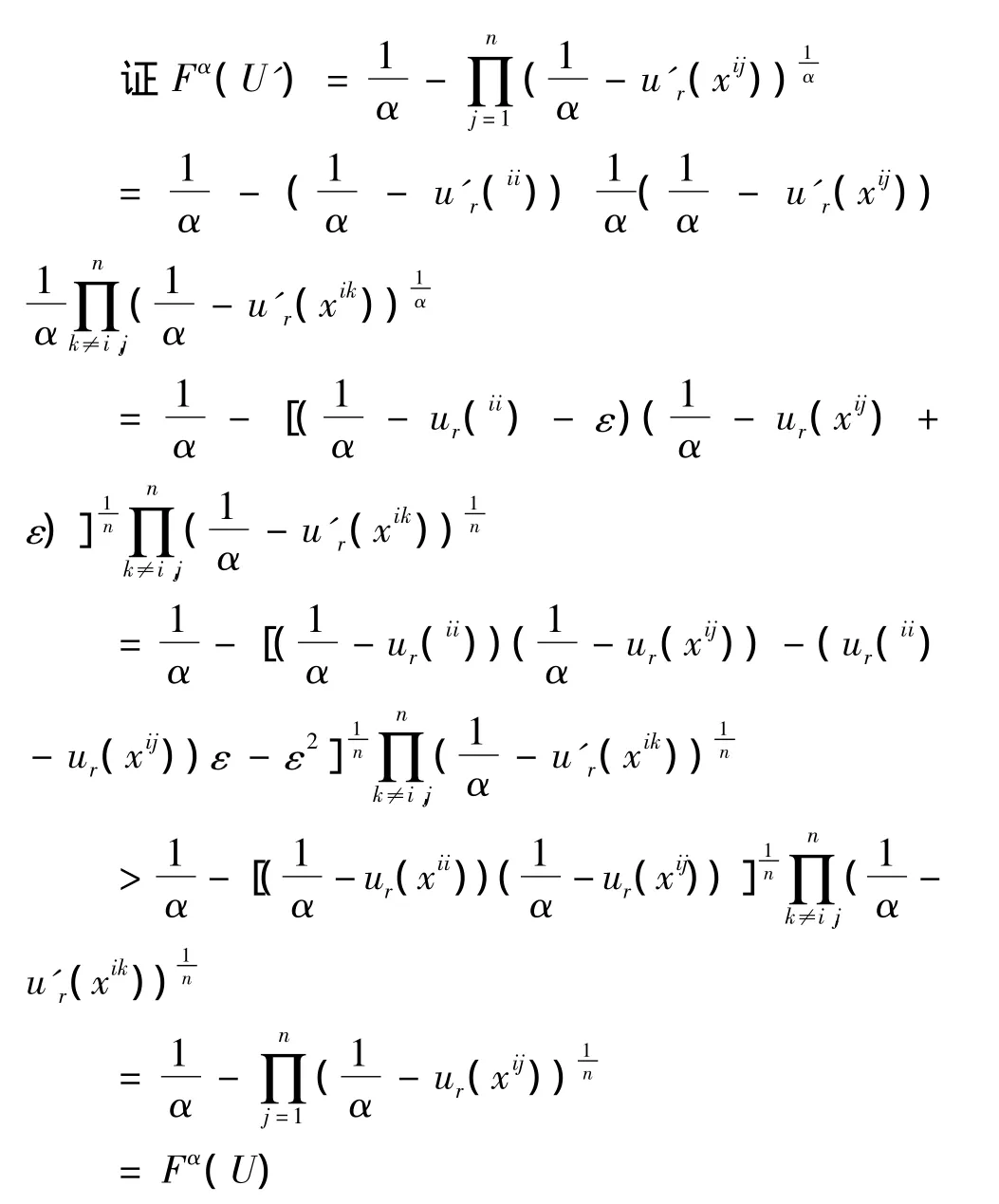
上述证明中之所以取“>”是因为ur(xii)≥u'r(xij),ε > 0,α ∈ (0,1)。
公理E[18](公平性公理)映射F满足公平性公理,如果对任意的U=(ur(xi1),ur(xi2),…,ur(xin))∈nu*,并且U≠U*,那么F(U)>F(U')
引理3 如果映射F满足传递性公理,那么其必满足公平性公理。
证 设F是满足传递性公理的映射,U=(ur(xi1),ur(xi2),…,ur(xin))和 U* =(u*,u*,…,u*)满足公平性公理中的条件,即U,U* ∈Δ,U≠U*,且有
定义集合S⊂Δ使得

这里有 U'=(u'r(xi1),u'r(xi2),…,u'r(xin)),u'r(xik)=ur(xik),∀ur(xik)≠(U),(U),且u'r(ii)=(U)+ ε(ur(xii)=(U)),u'r(xij)=(U)- ε(ur(xij)=(U)),由传递性公理,可以得到F(U)>F(φ(U))。考虑无限序列{U1,U2,…}使得U1=U且有Ut+1=φ(Ut)∀t>1。必然存在某个使得∀t≥,Ut=U*。因此 F(U1)>F(Ut)∀t>1,从而有F(U)>F(U*)。
引理4 任意的效用集结函数Fα,满足公平性公理。
公理C[17](一致性)映射F满足一致性公理,如果对任意的 U=(ur(xi1),ur(xi2),…,ur(xin))∈Δ,使得ur(xi1)=ur(xi2)= … =ur(xin)=u,则有F(U)=u。
公理A[17](匿名性)映射F满足匿名性公理,如果对任意的 U=(ur(xi1),ur(xi2),…,ur(xin))∈Δ,对所有的排列变换 σ:{1,…,n}→ {1,…,n},F(U)=F(ur(xiσ(1)),ur(xiσ(2)),…,ur(xiσ(n)))。
公理R(表示公理) 对于每个个体i,都存在一个函数vi:[0,1]→R+(R+表示正实数),并且对每个n∈Z+(Z+表示正整数),存在集结映射P:→R,使得对所有的效用函数值断面 U=(ur(xi1),ur(xi2),…,ur(xin))(ur(xij)∈ [0,1]),F(U)=P(v1(ur(xi1)),v2(ur(xi2)),…,vn(ur(xin)))和
(1)[18]对每个 i,v是仿射的和减的。
(2)[17]P 满足匿名性。即,对所有的 v=(v1,v2,…,vn)∈和排列 σ:{1,…,n}→ {1,…,n},P(v1,v2,…,vn)=P(vσ(1),vσ(2),…,vσ(n))。
(3)[18]P 满足标量独立性。即,由 P(v1,v2,…,vn)≥ P(v'1,v'2,…,v'n)和(b1,b2,…,bn)∈,可知 P(b1v1,b2v2,…,bnvn) ≥ P(b1v'1,b2v'2,…,bnv'n)。
3 充要条件
现在,给出并证明:一个效用集结函数可以用(1)式来表示的充分必要条件。
定理 映射F满足公理A,C,O和R当且仅当F可以用(1)式表出,即对任意的 U=(ur(xi1),ur(xi2),…,ur(xin))∈ Δ,有
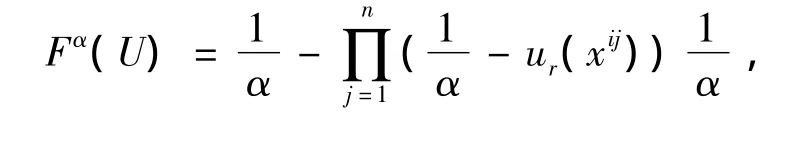
其中 α ∈ (0,1)。
证 先证明充分性条件,由上述知识,公理A,C,O显然成立。对于公理R,作代换,定义映射F如下:

可知(2)式满足公理R。
再证明必要性条件,设映射F满足公理A,C,O和R。由公理R,我们知道存在集结映射P使得,对任意的 U=(ur(xi1),ur(xi2),…,ur(xin))∈ Δ,
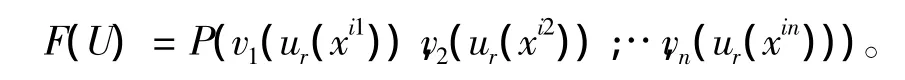
接下来分为四步来证明。
第一步:我们首先来证明P是元素乘积的变换,即

由公理R(ii)得
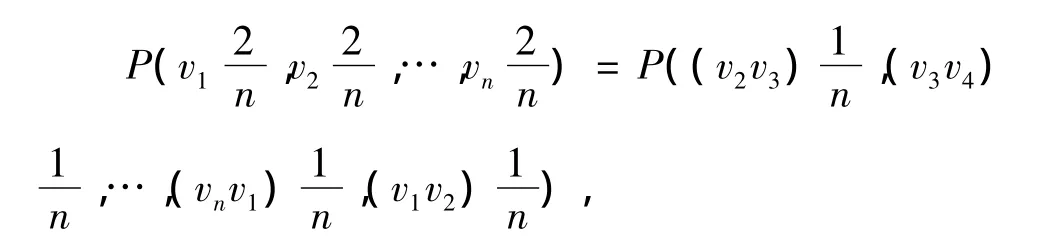
由公理R(iii)得

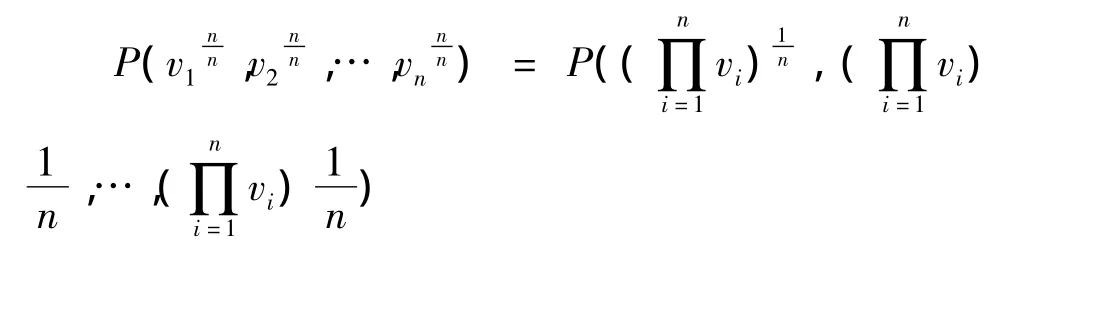
如果,那么就有P(v)=P(t)。因此,存在函数 ψ,使得
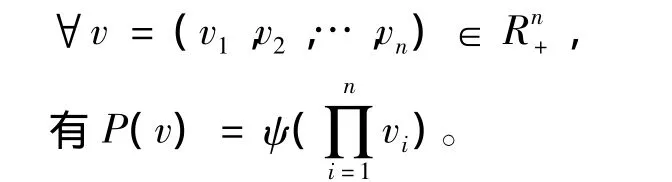
第二步:接着我们来证明P是元素乘积的负单调变换。也就是∃ψ:R→[0,1],使得x,y∈R,x > y,则ψ(x)> ψ(y)。设 U=(ur(xi1),ur(xi2),…,ur(xin))∈Δ和U'=(u'r(xi1),u'r(xi2),…,u'r(xin))∈Δ,并且 ur(xi1)> u'r(xi1),ur(xij)=u'r(xij),∀j∈ {2,3,…,n}。由公理O,F(U')> F(U)。由公理R,对每个i,vi是减函数,我们有
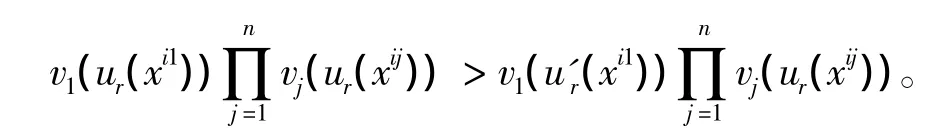
再利用公理R,可得
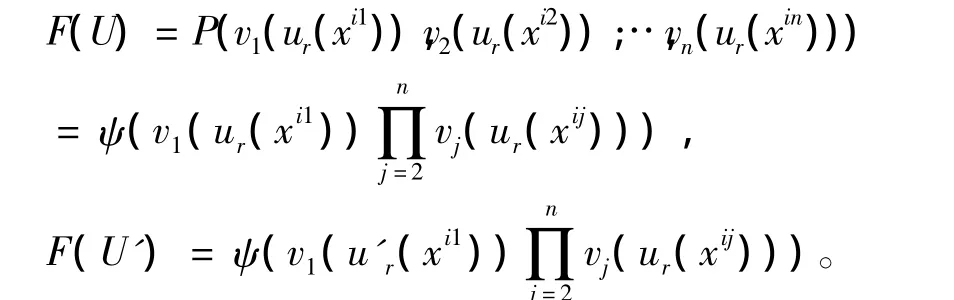
因此F(U')>F(U),从而ψ是减函数。由上述两步可知存在减函数ψ使得
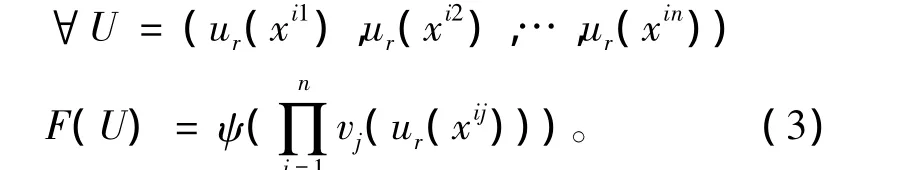
第 三 步: 考 虑 U =(ur(xi*),ur(xi2),…,ur(xin))∈ Δ,由公理 A,F(ur(xi*),ur(xi2),…,ur(xin))=F(ur(xi2),ur(xi*),…,ur(xin))。因此由
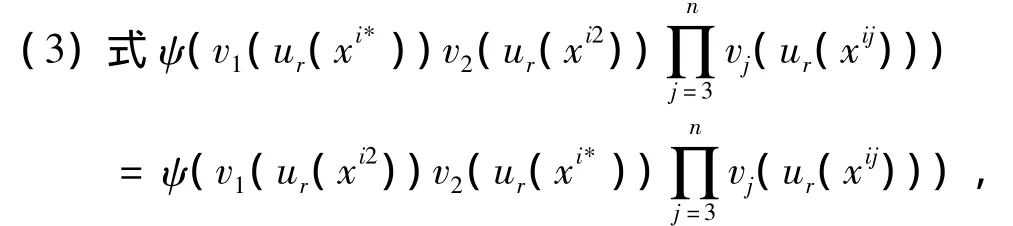
因为ψ是减函数,我们有
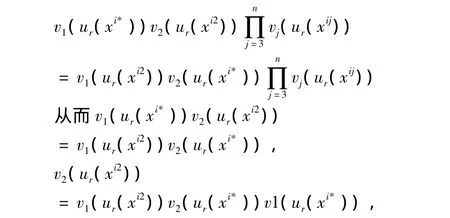
同理可得vj(ur(xij))=v1(ur(xij))vj(ur(xi*))v1(ur(xi*)),Vjj= 1,2,…,n。 因 此 ∀(ur(xi1),ur(xi2),…,里从上可知,如果存在减函数ψ满足(3)式,那么就存在减函数φ,使得 ∀U=(ur(xi1),ur(xi2),…,ur(xin))∈ Δ,
为了简单,我们用v(ur(xij))代替v1(ur(xij))则有

第四步:由公理 C,可知∀u∈[0,1],u=φ(v(ur(xij)n))。记 x=v(ur(xij)n),则有 φ(x)=v-1(),由公理 R(i),记 v(u)=A -Bu,B >0。因此 φ
利用(4)式有


因为v(1)=A-B>0,所以A>B,即α<1,又可知α>0。综上可知,必要性得证。
4 群体排序算法
最后,我们给出群体排序方法。
算法一:
(1)由各决策个体给出各组n个成员的效用值ur(xij);
(4)根据总体效用值U(i)的大小,对s个方案进行排序,U(i)值越大,方案越好。
算法二:
(1)由各决策个体给出各组n个成员的效用值ur(xij);
(2)计算第r个决策者对第i组n个成员的总效用值

(4)根据总体效用值Fα(U(i))的大小,对s个方案进行排序,Fα(U(i))值越小,方案越好。
[1] ARROW K J.Social Choice and Individual Values[M].New York:John Wiley & Son,1963.
[2] 胡毓达,胡的的.群体决策——多数规则与投票悖论.上海:上海科学技术出版社,2006.
[3] MAY K O.A set of independent,necessary and sufficient conditions for simple majority decision[J].Econometrica,1952,20:680-684.
[4] 王晓敏.群体决策的k-较多规则[J].上海交通大学学报,1995,29(3):168-170.
[5] 顾琼.群体决策的αk-较多规则[J].应用数学与计算数学学报,1997,11(2):86-88.
[6] KEENEY R L.A group preference axiomatization with cardinal utility[J].Management Science,1976,23(2):140-145.
[7] GREENBERG J.Consistent majority rules over compact sets of alternatives[J].Econometrica,1979,47(3):627-636.
[8] DYER J S,SARLIN R K.Group preference aggregation rules based on strength of preference[J].Management Science,1979,25(9):22-34.
[9] 胡毓达.随机偏爱群体决策和不可能性定理[J].自然科学进展,2002,12(6):580-584.
[10] 胡毓达,周轩伟,洪振杰.随机偏爱群体决策的随机偏爱数法[M]//第二届全国决策科学/多目标决策研讨会论文集(温州大学学报,特刊).2002,15(3):11-15.
[11] HU Yu-da,HU Di-di.A class of stochastic λ – Borda number rule for group decision making[M]//Proceedings of 4thNational Conference on Decision Making Sciences/Multiple Criteria Decision Making(Transactions of Operations Research),2007,5:167-171.
[12] 李静,胡毓达.群体决策的较多随机偏爱规则.上海交通大学学报,2007,41(10):313-317.
[13] CESAR Calvo,STEFAN Dercon.Measuring Individual Vulnerability[J].Economic Journal,2003,113:95-102.
[14] SEN A.Poverty:An ordinal approach to measurement[J].Econometrica,1976,44:219-231.
[15] BANERJEE A,DUFLO E.The Economic lives of the Poor[J].Journal of Economic Perspectives,2007,21(1):141-167.
[16] HULME D,SHEPHERD A.Conceptualizing chronic poverty[J].World Development,2003,31(3):403-423.
[17] 阿马蒂亚·森.集体选择与社会福利[M].胡的的,胡毓达,译.上海:上海科学技术出版社,2004.
[18] CHEW Soo Hong.A Generalization of the Quasilinear Mean with Applications to the Measurement of Income Inequality and Decision Theory Resolving the Allais Paradox[J].Econometrica,1983,51(4):1065-1092.
