二元关系传递性的等价定义及其判别法
2014-05-25孙凤芝
孙凤芝
(大庆师范学院 教师教育学院,黑龙江 大庆163712)
0 引言
二元关系是离散数学中重要的基本概念,实际判定某个二元关系性质时,自反性、反自反性、对称性的判定比较容易,而传递性的判定有时则较困难,是学习的重点,也是难点。一方面,本文给出二元关系传递性的等价定义,得到解决途径:从逻辑蕴涵式的角度,给出一种等价的定义形式,该定义把判断集合A 上的二元关系R 是否具有传递性问题转化为判断蕴涵式的真假问题;另一方面,本文利用二元关系与其关系矩阵是一一对应的结论,给出矩形判别法,这样就突破了难点,使对二元关系传递性的判定准确而又迅速。
1 二元关系传递性的定义及其局限性
在现有的离散数学教材文献[1][2]中,对二元关系反对称性和传递性分别定义如下:
定义1 :设R 为集合A 上的二元关系,对于(x,y,z ∈A,当<x,y >∈R 且<y,z >∈R 时,有<x,z >∈R,则称R 在A 上具有传递性。
例1:设集合A={1,2,3,4},R 是A 上的二元关系,R={<1,2 >,<3,4 >},问R 在A 上是否可传递?
分析:正确答案为“R 在A 上是可传递的。”许多同学对此感到困惑,提出疑问:他们认为在A 中找不到元素x,y,z,使得<x,y >∈R,<y,z >∈R,当然也更谈不到<x,z >∈R 了,所以他们认为R 在A 上是不可传递的。可见,直接根据传递性的定义不好判定二元关系的传递性。
2 二元关系传递性的等价定义及应用
在课程安排的先后顺序上考虑,把数理逻辑安排在二元关系(集合论)之前讲,把定义用逻辑部分的符号语言等价地表示出来,即得第二等价定义。
传递性等价定义 对于集合A 上的关系R,若
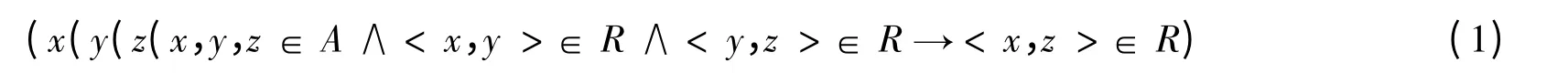
为真,则称R 在A 上具有传递性。
从上述定义中可以看出,定义的表达形式是蕴涵式,从而可以把判断集合A 上的二元关系R 是否具有传递性问题转化为判断定义中蕴涵式(1)式的真假问题。
应用传递性第二等价定义可以很快地判定前面例1 的传递性
例2:设集合A={1,2,3,4},R 是A 上的二元关系,R={<1,2 >,<3,4 >},问R 在A 上是否可传递?
解:对R 中的有序对<1,2 >,不存在<2,x >∈R,即<2,x >(R(- x ∈A),蕴涵式的前件为假,蕴涵式为真;
对R 中的有序对<3,4 >,不存在<4,x >∈R,即<4,x >(R(- x ∈A),蕴涵式的前件为假,蕴涵式为真;
因此,R 中的每一个有序对都使传递性定义等价形式中的蕴涵式为真,该二元关系是传递的。
3 二元关系的判别法及其应用
3.1 有关定义、定理及其证明
定义2:对于A 是有穷集合时,设A={x1,x2,…,xn},R 是A 上的关系,
是R 的关系矩阵,记做MR。
定义3:设F,G 为二元关系,G 对F 的右复合记作F °G,其中
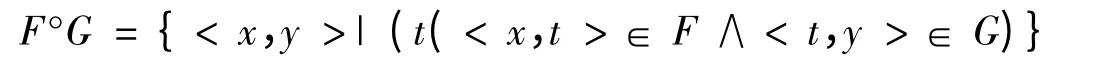
由传递的关系的定义1 及右复合运算的定义3,我们有以下的定理。
引理:设R 为A 上的关系,则R 在A 上传递当且仅当R°R ⊆R
由引理与关系矩阵定义2 及右复合运算的定义3,我们有以下的定理。
定理:设R(A×A,其中A 为有限集合(不妨设为n 元素集合),MR是R 的关系矩阵,则R 是可传递的当且仅当在MR中,对于任意的k,若有aik=akj=1(1 ≤i,j ≤n),则必有aij=1.
证明:不妨设A={a1,a2,…,an}。对于任意的i,j(1 ≤i,j ≤n),若存在<ai,aj>∈R,则在MR中有aij=1;否则aij=0.反之亦然。
必要性:R 是可传递的,即若对于任意ai,aj,ak∈X,每当(<ai,ak>∈R)∧(<ak,aj>∈R)时必有<ai,aj>∈R,则有在MR中,对于任意的k,若有aik=aki=1,则必有aij=1。
充分性:已知在MR中,对于任意的k,若有aik=akj=1(1 ≤i,j ≤n),则必有aij=1。进而有对于任意ai,aj,ak∈X,每当(<ai,ak>∈R)∧(<ak,aj>∈R)时,必有<ai,aj>∈R。故证得R 是可传递的。
3.2 矩形判别方法与应用
由上述定理,在R 是可传递的等价条件中所涉及的关系矩阵MR中元素aik、akj及aij再加上主对角上元素akk,如果将这四个点用直线分别沿所在的行和列连起来,则恰好构成一个矩形,由此可以得到传递关系R 的矩形判别法:
(1)依次选取MR中主对角线上元素akk(k=1,2,3,...,n)(并以此元素为中心点划横、纵线各一条,即在第k 行与第k 列上各划一条线,可用实线表示);
(2)对第k 行元素中依次找出所有非零元素,设为akj(1 ≤j ≤n),(并在此元素所在的第j 列上划一条线,可用虚线表示),显然,akj=1;
(3)对(2)中的每个元素akj,在第k 列元素中依次找出所有非零元素,设为aik(并在此元素所在的第i行上划一条线,可用虚线表示),显然,aik=1;
(4)判别:若对于(2)、(3)中所有非零元素aik、akj,元素aij非零(即(2)、(3)中两条虚线的交点处的元素非零),则可以判别关系R 是可传递的(见图1)。

图1 传递关系R 的矩形判别法
注:1)在中,akk只是提供了判别的一个顺序号,使思路清晰,不重不漏,而akk=0 还是akk=1,对判别没有影响;
2)在判别方法中,亦可将(2)、(3)中的“行”“列”互换;
3)若要验证或判别关系R 是可传递的,则须在MR中对于每一个k(k=1,2,3,...,n)验证出对于所有的i,j(1 ≤i,j ≤n),或者aik与akj至少有一个为零,或者aik、akj或者aij都等于1.=0
例3 设A={a1,a2,a3,a4,a5,a6},
R={(a1,a2),(a1,a3),(a1,a4),(a2,a3),(a2,a4),(a3,a4),(a1,a6),(a5,a4),(a6,a2),(a6,a3),(a6,a4)},
试判断R 是传递关系吗?
方法一:用矩形判别法判别R 是传递的:
当k=1 时,由于在第1 列中元素均为0,故进行下一步;
当k=2 时,第2 行中有两个元素a23=1,a24=1,而在第2 列中有两个元素a12=1,a62=1,由此只须进行四次判别:
在a23=1 且a12=1 的情况下判别是否有a13=1;
在a23=1 且a62=1 的情况下判别是否有a63=1;
在a24=1 且a12=1 的情况下判别是否有a14=1;
在a24=1 且a62=1 的情况下判别是否有a64=1;
由MR知a13=1,a63=1,a14=1,a64=1。
当k=3 时,情况与k=2 时类似,……
当k >3 时,读者可类似地讨论。
例2 已知
A={a,b,c,d,e,f},R={<a,a >,<a,b >,<a,c >,<a,f >,<b,b >,<b,c >,<b,f >,<d,a >,<d,b >,<d,c >,<d,d >.<d,f >,<e,a >,<e,b >,<e,c >,<e,d >,<e,e >,<e,f >,<f,a >,<f,b >},试判断R 是否是传递关系。
方法二:
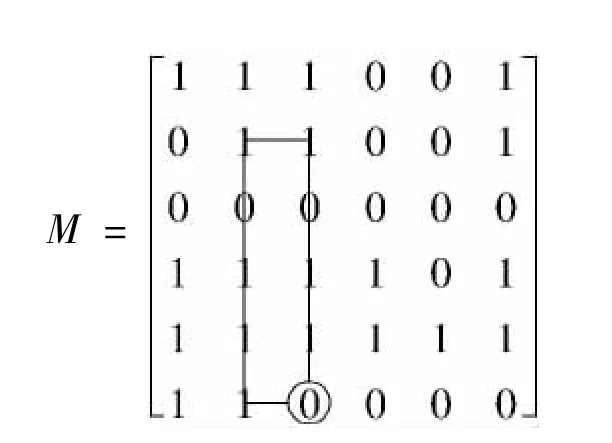
图4 传递关系R 的矩形判别法
由矩形判别法,如图4,因为a62=1,a23=1,而交叉点a63=0,所以,R 不是传递关系。
4 结 语
通过给出二元关系传递性的等价定义和矩形判别法,并通过实例对它们进行了应用,使对二元关系传递性的判断直观、高效。
[1]左孝凌,李为鉴,刘永才.离散数学[M].上海:上海科学技术文献出版社,1982.
[2]耿素云,屈婉玲,张立昂.离散数学[M].北京:清华大学出版社,1991:75-86.
[3]耿素云,屈婉玲.离散数学[M].北京:高等教育出版社,1997:1-105,132-156.
[4]Kolman B,Busby R C,Ross S C.Discrete Mathematical Structures[M].Beijing:Higher Education press,2001.
[5]杨思春,王小林.二元关系传递性研究[J].微机发展,2003,13(10):88-89.
