马尔科夫模型在大学生转专业趋势预测中的应用

程 伟

安徽电子信息职业技术学院，安徽蚌埠，233040

学生填报高考志愿选择专业时应全面考虑专业在职业生涯中的作用，了解自己的兴趣爱好、人格特征、能力倾向以及价值观，同时要掌握所填报专业的就业情况、课程设置等［1］；否则，会为将来就业埋下隐患。

但不少学生、家长对社会就业状况、学校专业设置缺乏详细认知，只是凭分数填报志愿。当发现专业的选择与以后的学习及自身能力、兴趣、职业发展相差很远时，才决定重新选择专业。这样，就出现了学生转专业现象。

学生重新选择专业，对学生的能动性和个性的发挥都是有利的，也有利于今后学生的发展。但对学生的转专业现象要做好教育和引导工作，告诫学生要把握好自己，学会选择［2-3］。同时转专业也带来一些负面影响，如教学资源浪费、专业建设不均衡、师资队伍不平衡、学生难于管理等。学校要及早掌握转专业态势，做好应对准备。因此，对大学生转专业状态趋势预测很有必要。然而，目前对大学生转专业状态趋势的预测还很少有研究，为此，本文利用马尔科夫链的相关原理建立模型，对大学生转专业状态趋势进行预测。

1 马尔科夫链及其特性

1．1 马尔科夫链

定义 在概率空间（Ω，F，P）上的随机序列X0，X1，…，如果满足以下两个条件：

（1）｛Xn：n≥0｝的状态空间为可数集；

（2）对任意n以及状态i0，i1，…，in＋1，只 要P｛X0＝i0，X1＝i1，…，Xn＝in｝≥0，就有

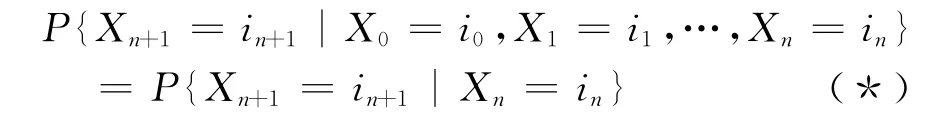
称序列X0，X1，…，为（离散参数）马尔科夫链。

1．2 马尔科夫链的无后效性

设一个作随机运动的质点，以Xn表示质点在时刻n所处的位置，Xn＝i表示质点在时刻n处于状态i这一事件。如果把时刻n看成“现在”，则时刻0，1，…，n-1都表示“过去”，而时刻n＋1表示“将来”。则（＊）表示在已知过去X0＝i0，X1＝i1，…，Xn-1＝in-1以及现在Xn＝in的条件下，质点在时刻n＋1处于状态i＋1的条件概率，只和现在发生的事件有关，而与过去发生的事件无关。即马尔科夫链表示在已知“现在”的条件下，“将来”与“过去”无关。这就是马尔科夫链的无后效性，它是马氏链的特征。

1．3 齐次马尔科夫链及转移矩阵

如果对任意m，n和状态i，j，只要P｛Xn＝i｝＞0，P｛Xm＝i｝＞0，就有

P｛Xn＋1＝j｜Xn＝i｝＝P｛Xm＋1＝j｜Xm＝i｝称马尔科夫链为齐次的。对于齐次马尔科夫链，称Pij＝P｛Xn＋1＝j｜Xn＝i｝为｛Xn：n≥0｝的转移概率。它表示质点在时刻n自状态i出发，与时刻n＋1转移到状态j的概率。当i，j在状态空间E中变化时，由Pij定义的矩阵P＝｜pij｜称为｛Xn∶n≥0｝的转移矩阵。一般而言，转移矩阵为：

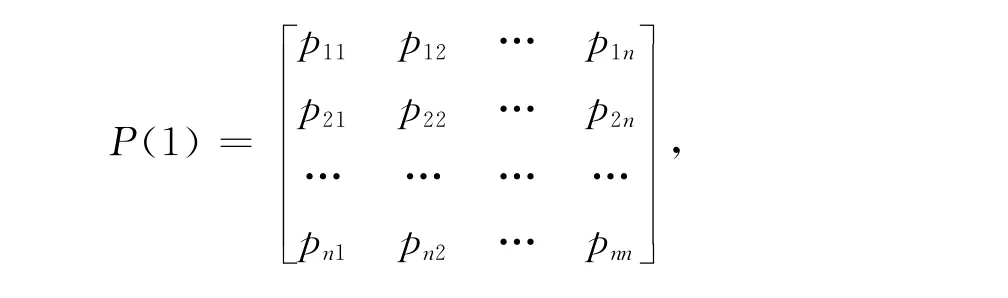
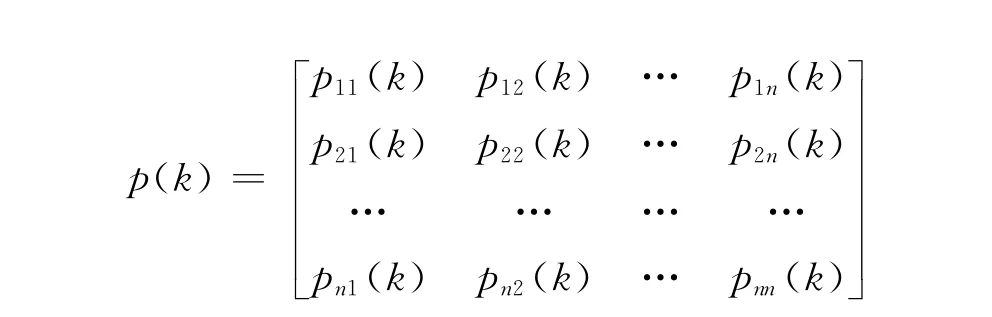
从马尔科夫链的定义可以看出，其无后效性是可以预测事物发展趋势的。马尔科夫模型预测方法的特点是：在近期有限资料的情况下，可对现状进行定量预测，而不需要过去的大量统计资料，这与其他预测方法相比，使得它在应用上带来许多便利。如果系统变化不大，还可以利用多次转移矩阵滚动进行长期预测［4］。这里通过调研所得数据，运用马尔科夫链模型来预测大学生转专业状态趋势。

2 马尔科夫预测模型的建立

本文以某学院2011年、2012年考生录取情况及报到后学生转专业情况来收集数据。样本采集涉及电子类专业、计算机类专业、经管类专业的学生。一般而言，学生未来转专业的趋势只与目前的情况有关，而与以前的情况关系较小，理论上可以视作无关，因此，可以运用马尔科夫链建立学生转专业趋势的预测模型。

2．1 预测模型的计算方法

利用状态转移概率和系统的初始状态，可以建立马尔科夫预测模型，方法如下：

设系统初始状态时，k＝0。经过k次转移后，达到状态的概率为Si（k），则有：∑Si（k）＝1

由切普曼柯尔莫戈诺夫方程得：

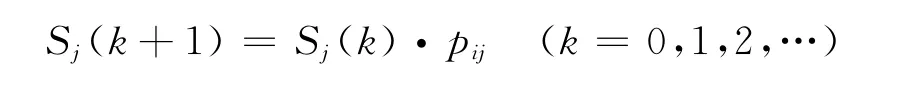
用向量表示：

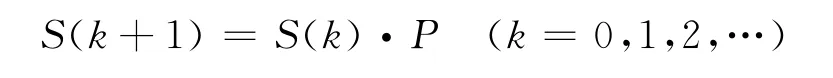
可得递推公式：

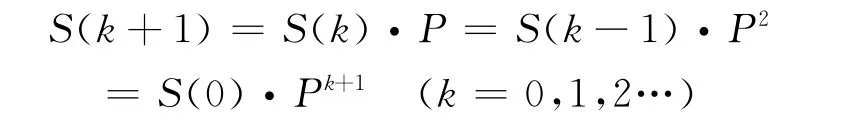
利用此公式可对系统进行预测。

2．2 案例分析

按学生所属专业大类，可以将学生分为电子类、计算机类、经管类三个类别。对某学院2011级新生录取及转专业情况进行调研，获得相关数据（表1）。

从表1可以看出，2011级电子类、计算机类、经管类的新生录取人数分别为1 473、952、545。由于各方面原因，部分学生到校后申请转专业，其中电子类保留新生1 304人，保留概率为1304／1473＝0．885268；转计算机类新生概率为53／1473＝0．035981；转经管类 新生 概 率 为 116／1473 ＝0．078751。以同样方法可计算出计算机类、经管类的新生保留与转向的概率（省略）。经过转专业后的电子类、计算机类、经管类新生的实际占有数分别为1412、864、694，占有率分别为0．475421、0．290909、0．23367，即初期（0．475421 0．290909 0．23367）。

表1 某学院2011级学生录取及转专业情况

利用转移概率，可得转移矩阵为：

根据切普曼柯尔莫戈诺夫方程可预测2012级电子类、计算机类、经管类新生的占有率S（1）：

即2012级的电子类、计算机类、经管类新生占有率的预测值分别为0．457696，0．266161，0．276144。

2．3 预测数值分析

要对模型进行检验，判定其合理、合格后才能用作预测。

根据实际调查结果，得到2012级电子类、计算机类、经管类新生实际占有率，见表2，将它与预测值进行数值分析，得以下结果。

表2 2012级新生占有率预测值与实际值间的误差

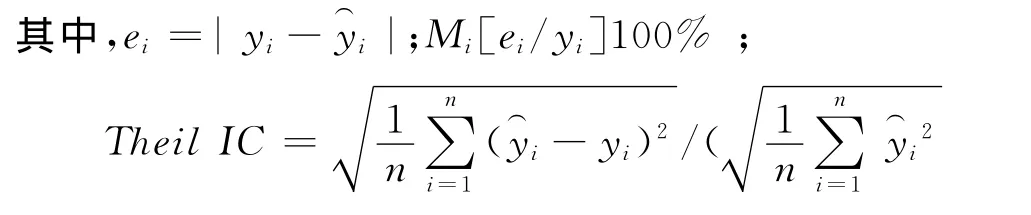
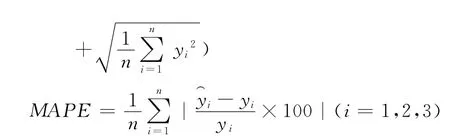
下面对模型进行数值分析，其中包括属于绝对数值分析的绝对误差，属于相对数值分析的相对误差、希尔不等系数和平均绝对百分误差［5］。

绝对误差分析：绝对误差在0．003～0．01之间，比较小。

相对误差分析：相对误差在1．25%～2．5%之间，也比较小。

希尔不等系数（Theil IC）分析：希尔不等系数是数值越小，真实值与预测值越小，其预测精度越高。希尔不等系数通常在0到1之间。从表2看，预测模型的希尔不等系数（Theil IC）值为0．010 945 1，远远小于1，说明此模型的预测准确度较高。

平均绝对百分误差（MAPE）分析：如果MAPE的值不超过10，就认为其预测精度较高。从表2看，预测模型得到的MAPE值为2．02507672，其值小于10，说明其模型预测精度很好。

通过以上数值分析，可以认为用马尔科夫预测法对新生占有率进行预测是十分可行的。因此在系统状态相对稳定的情况下，利用转移矩阵可继续预测2013级新生的占有率S（2）。由下式可得：

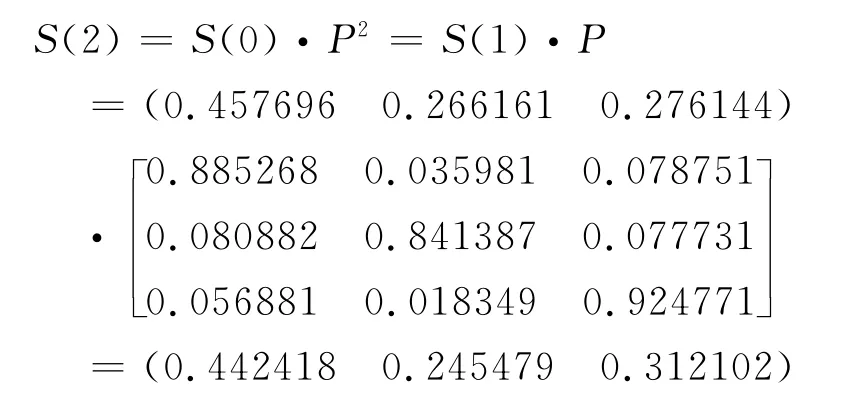
即2013级的电子类、计算机类、经管类新生占有率的预测值分别为0．442418，0．245479，0．312102。

3 根据预测结果，采取相关策略，保持合适的新生占有率

预测学生类别的占有率可对学校的招生工作、专业设置、教学改革提供参考。某学院是一个以工科为主的高职院校，电子类、计算机类、经管类学生比例应该以4．2∶3．0∶2．8为宜。随着高考的扩招，文科考生的增加，某学院招生也以理科为主改为文理兼收，这样学生进校后转专业的需求也越来越大。由预测结果可以看出，转专业后电子类、计算机类学生比例逐年下降，而经管类学生逐年增加，如果大量学生转专业将造成专业结构的不平衡，也造成资源浪费。根据预测结果，学校可采取以下相关策略，保持适宜的学生比例，使教学资源高效利用，师生比例适宜，教学计划正常进行。

3．1 根据社会需求，优化专业结构

主动适应产业和区域经济发展需求，调整专业设置与计划编制，优化专业结构，使专业设置更加贴近市场，符合经济社会与区域经济建设的实际需要，以形成以电子类专业为主，计算机类、经管人文类等专业平衡发展的格局。

3．2 加强专业介绍，强化职业教育

专业教师和招生就业部门，在新生填报志愿及报到时加强对考生、家长进行详细的专业介绍和职业教育，加强新设专业宣传，提高新专业知名度与认可度，使他们了解专业特点和就业方向，稳定专业思想，凝聚人心。

3．3 按大类招生，再确定方向

学校按大类招生，大一不分专业，教学按大类展开，考生根据自身情况和兴趣，报考时先选择专业大类，大二以后，通过通识课和专业基础课的学习，加深对专业的理解，再开始分专业，确定专业方向。

3．4 提升教学质量，激发学习兴趣

通过师资培训、定期选派各专业教师到校外实习基地一线工作，提高教师的理论与实践联系的能力，提升课堂教学质量。同时紧紧围绕专业建设，加强技能训练，激发学生的学习兴趣，树立对专业的学习信心。

4 结语

随着就业形式的变化和高校可持续发展的需要，大学生转专业现象已在高校相当普遍。为合理分配教学资源，优化专业结构，对大学生专业趋势预测很有必要。将马尔科夫链引入到大学生转专业预测中，从理论和应用实例看，该方法较为简单、易行，并根据预测结果对保持专业学生适宜的占有率进行了探究，为招生就业、专业设置、教学管理等工作提供了依据。

［1］王勤．高考学生专业选择与专业兴趣相符性研究［J］．黑龙江高教研究，2004（9）：20-22

［2］李爱国．大学生转专业的现状分析与思考［J］．中国成人教育，2009（23）：35-36

［3］程墨，朱建华．新生竞相转专业高校应积极引导［N］．中国教育报，2008-10-07（03）

［4］邓大松，孟颖颖．对我国农村剩余劳动力流动趋势的预测［J］．统计与决策，2008（15）：94-96

［5］易丹辉．数据分析与Eviews应用［M］．北京：中国统计出版社，2002：43-45