第一性原理计算Al元素含量对高熵合金AlxCoCrCuFeNi的影响
2014-07-13王兰馨
王兰馨,姚 山,温 斌
(1.大连理工大学材料科学与工程学院,大连116024;2.燕山大学亚稳材料国家重点实验室,秦皇岛066004)
1 引 言
近年来,高熵合金的研究已成为材料研究的热点之一,它突破了传统的以一种或两种元素为主元的合金设计,发展出一种新的合金设计理念[1-12].高熵合金至少是5个等原子比或近似等原子比组元,但是不能超过35%,因此没有一个元素能占有50%以上[2-4].目前的研究结果表明[13-15],高熵合金凝固后不仅不会形成数目众多的金属间化合物和复杂相,反而形成具有体心立方或面心立方等简单晶体结构的固溶体相甚至非晶质,所形成的相数要远远低于平衡相率所预测的相数.也就是说,合金中的高熵效应有效的抑制了脆性金属间化合物的出现,并能够促进元素间混合形成简单的体心立方或面心立方结构甚至非晶结构.多元高熵合金的特性是多个主要元素的共同体现,因此具有很多传统合金所不具有的优异特性[16-18],例如通过适当的合金配方设计,能获得高硬度、高加工硬化、耐高温软化、耐高温氧化、耐腐蚀、高电阻率等特性组合,因此高熵合金在实际中有很大的应用潜力.目前针对高熵合金的研究越来越多,以AlCoCrCuFeNi合金系为例,自2004年由叶均蔚等人成功合成以来[4],对其各方面的研究也与日俱增.如在Al0.5CoCrCuFeNi中加入不同含量的硼后的耐磨性与高温压缩性能的研究[5],Al元素含量不同对微观结构[6]及机械性能的影响[7],Al元素含量与其粘着磨损性能的关系[8],及各个元素含量不同对其微观结构和硬度的影响[9]等等.但是,由于高熵合金合成较复杂,尤其是稍微改变所含元素含量过程更难控制,对其它性能的研究结果非常有限.第一性原理从头计算不需要任何参数,只需要一些基本的物理常量就可以得到体系基态的基本性质.其中的密度泛函理论是一种研究多电子体系电子结构的量子力学方法,在研究分子和凝聚态的性质中应用非常广泛.如第一性原理计算Al-Ni系金属间化合物的性质[19],Ni-Ta系金属间化合物的性质[20],及计算Ca-Zn系金属间化合物的结构性能和弹性能[21]等等.因此,本文采用第一性原理密度泛函理论和平面波赝势的方法计算高熵合金AlxCoCrCuFeNi的结构性能,弹性能,生成热等性质.其中x表示Al元素的摩尔含量,分别为0,0.5,1,1.5,2,其余元素的摩尔含量均为1.
2 计算方法
本文的第一性原理密度泛函理论计算采用基于平面波赝势法的CASTEP软件包[22],固溶体结构模型采用虚拟晶体近似(VCA)[23-25]的方法建立.由于高熵固溶体合金AlxCoCrCuFeNi具有不完全有序的体心立方结构[15],为了避免使用虚拟晶体近似方法建模过程中产生的所谓的“虚拟原子”[24]和长程结构中所累积的误差[25],本文在单个晶胞中建立体心立方结构,在体心立方中的原子上使用虚拟晶体近似.计算过程中,电子间交换-相关作用采取GGA[26]近似下的PBE 泛函[27],采用基于第一性原理的模守恒赝势[28]处理电子-离子相互作用,计算中平面波函数展开的动能截断取为550eV,倒空间中k点网格间距选为0.04Å-1,剖分网格为10×10×10.
在以上计算设置条件下,对计算结果的准确性进行了验证.通过验证计算,体心立方结构Fe晶格常数2.84 Å,与实验值2.87 Å[29]能够很 好吻合,由此可见,本文所选取的计算设置比较合理.
3 结果与讨论
3.1 结构性质
在所设置的计算条件下,本文对高熵合金AlxCoCrCuFeNi(x=0,0.5,1,1.5,2)的结构进行了优化,优化后的晶格常数和密度在表1中列出,为了直观起见,在图1中画出了晶格常数和密度的对比结果.由表1和图1可以看出,随着Al元素摩尔含量增大,高熵合金AlxCoCrCuFeNi的密度减小,Al元素的摩尔含量为0.5 时,高熵合金Al0.5CoCrCuFeNi的密度最大,为8.289g/cm3.当Al元素的摩尔含量为1时,高熵合金AlCoCrCuFeNi的晶格常数最小,为2.791Å,增大或减小Al元素的摩尔含量,高熵合金AlxCoCrCuFeNi的晶格常数都会增大.
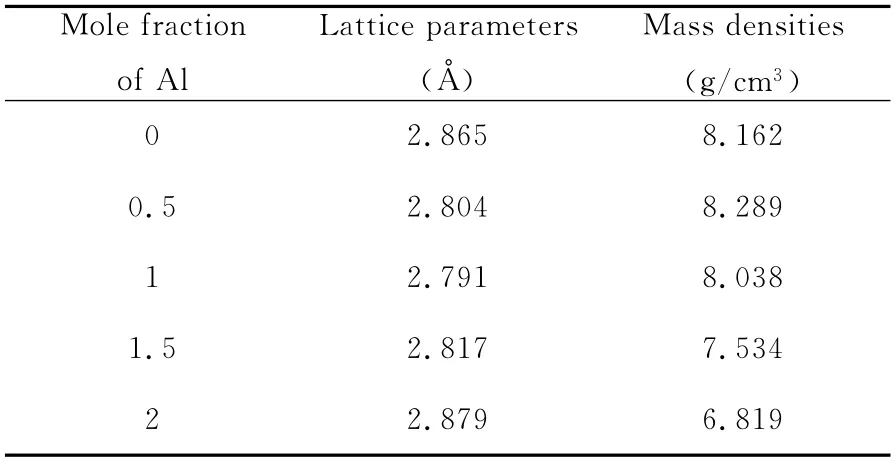
表1 高熵合金AlxCoCrCuFeNi(x=0,0.5,1,1.5,2)的晶格常数和密度Table 1 The lattice parameters and mass densities of the high entropy alloy AlxCoCrCuFeNi with x=0,0.5,1,1.5and 2,respectively
3.2 弹性性质
在优化高熵合金AlxCoCrCuFeNi的晶格结构后,本文仍采用第一性原理密度泛函理论计算了其弹性常数Cij、杨氏模量E、体积弹性模量K 及泊松比ν.表2中列出了不同Al元素摩尔含量的高熵合金AlxCoCrCuFeNi的弹性常数Cij,由于其结构为立方晶体,因此弹性常数只有C11、C12及C44.弹性常数决定了材料的力学稳定性,根据立方晶体的判据[30]:
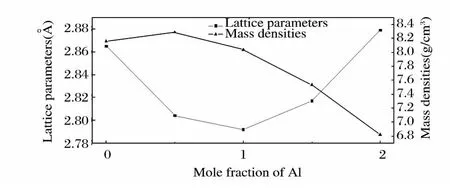
图1 高熵合金AlxCoCrCuFeNi在Al含量不同时晶格常数与密度的比较Fig.1 Comparisons of the lattice parameters and mass densities among the high entropy alloys AlxCoCrCuFeNi when the mole fraction of Al changed

高熵合金AlxCoCrCuFeNi只在Al元素摩尔含量为2时才符合力学稳定性条件.

表2 高熵合金AlxCoCrCuFeNi(x=0,0.5,1,1.5,2)的弹性常数Table 2 The elastic constants Cij(GPa)of the high entropy AlxCoCrCuFeNi with x=0,0.5,1,1.5and 2,respectively
表3列出了高熵合金AlxCoCrCuFeNi的杨氏模量E、体积弹性模量K 及泊松比ν.图2画出了杨氏模量与体积弹性模量随着Al元素摩尔分数的变化.可以看出,当Al元素的摩尔含量为1时,高熵合金AlCoCrCuFeNi的杨氏模量最小而体积弹性模量最大.为了进一步了解高熵合金的力学稳定性,本文采用Voigt-Reuss-Hill(VRH)的方法[31]计算了高熵合金AlxCoCrCuFeNi的体积弹性模量KV、KR、KH和剪切模量GV、GR、GH,其结果列于表4 中.由结果可以明显看出,采用VRH方法计算的体积弹性模量没有明显变化,剪切模量的计算结果有较大差异.当Al元素的摩尔含量为2时,采用VRH 方法计算的高熵合金Al2CoCr-CuFeNi其体积弹性模量和剪切模量都变化不大.
金属材料的脆/韧性取决于泊松比或是剪切模量与体积弹性模量的比值.材料的泊松比为1/3左右时可视为韧性材料,其余为脆性材料[32];剪切模量与体积弹性模量的比值为0.57是材料脆/韧性的分界点,当比值大于0.57时,视为脆性材料,小于0.57时,视为韧性材料[33].表5 列出了高熵合金AlxCoCrCuFeNi的泊松比及剪切模量与体积弹性模量的比值,以泊松比为依据时,高熵合金Al2CoCrCuFeNi为韧性材料,其余为脆性材料;以剪切模量与体积弹性模量的比值为依据时,高熵合金Al1.5CoCrCuFeNi和Al2CoCrCuFeNi可视为韧性材料,其余为脆性材料.

表3 高熵合金AlxCoCrCuFeNi(x=0,0.5,1,1.5,2)的杨氏模量E、体积弹性模量K 及泊松比νTable 3 The Young’s modulus,bulk modulus,Possion’s ratios of the high entropy alloys AlxCoCrCuFeNi with x=0,0.5,1,1.5and 2,respectively

图2 杨氏模量和体积弹性模量与Al元素摩尔分数的关系Fig.2 The relationships of Young’s modulus and bulk modulus to the mole fraction of Al

表4 采用VRH 方法计算的高熵合金AlxCoCrCuFeNi(x=0,0.5,1,1.5,2)的体积弹性模量和剪切模量Table 4 The bulk modulus,shear modulus for the high entropy alloy AlxCoCrCuFeNi with x=0,0.5,1,1.5and 2,respectively

表5 高熵合金AlxCoCrCuFeNi(x=0,0.5,1,1.5,2)的泊松比及剪切模量与体积弹性模量的比值Table 5 Calculated Poisson’s ratiosν,ratios of shear modulus to bulk modulus for the high entropy alloy AlxCoCrCuFeNi with x=0,0.5,1,1.5 and 2,respectively
3.3 生成热及热力学稳定性
本文优化了高熵合金AlxCoCrCuFeNi及各个金属元素单质的晶格结构后,可以得到高熵合金AlxCoCrCuFeNi的基态总能量及平衡晶体结构.因此高熵合金AlxCoCrCuFeNi的生成热就可以由下式算出:

其中Eform为高熵合金的生成热,Etotal为高熵合金的基态总能量,xele和Eele分别是金属元素单质的摩尔分数和平衡晶体结构下的单原子总能量.采用公式(2)计算的高熵合金AlxCoCrCuFeNi的生成热列于表6中,其随Al元素摩尔分数的变化如图3所示.由于金属材料的热力学稳定性由其吉布斯自由能决定,吉布斯自由能是熵与生成热的和.但是由于高熵合金的定义可知其混合熵很大[2-8],因此高熵合金的吉布斯自由能有很大一部分来自熵的贡献,即熵对热力学稳定性的影响不可忽视.但是本文所采用的第一性原理密度泛函理论计算设置为0K 的条件下,没有考虑熵的影响,因此将在以后进一步研究高熵合金其熵对热力学稳定性的影响.

表6 高熵合金AlxCoCrCuFeNi(x=0,0.5,1,1.5,2)的生成热Table 6 The heat of formation of the high entropy alloys with x=0,0.5,1,1.5and 2,respectively
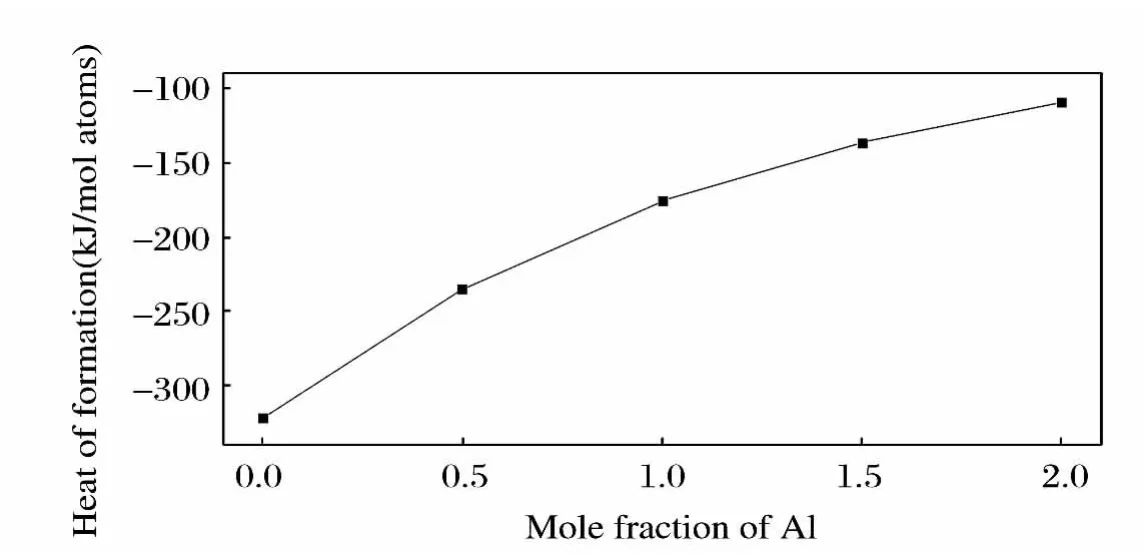
图3 高熵合金AlxCoCrCuFeNi(x=0,0.5,1,1.5,2)生成热与Al元素摩尔含量的关系Fig.3 The relationship between the heat of formation for the high entropy alloy AlxCoCr-CuFeNi and mole fraction of Al with x=0,0.5,1,1.5and 2,respectively
在本文的计算条件下,生成热就决定了高熵合金的热力学稳定性.由表6 可知高熵合金AlxCoCrCuFeNi的生成热皆为负值,因此可看作其在热力学的条件下是稳定的.由图3可以看出,随着Al元素摩尔含量的增大,高熵合金AlxCoCrCuFe-Ni的生成热也随之增大.
4 结 论
本文对高熵合金AlxCoCrCuFeNi的结构性能、弹性能及热力学相对稳定性开展第一性原理计算,得到以下结论:1、随着Al元素摩尔含量增大,高熵合金AlxCoCrCuFeNi的密度减小,当Al元素摩尔含量为1 时,其晶格常数最小;2、高熵合金AlxCoCrCuFeNi在Al元素摩尔含量为2 时符合力学稳定性条件,以泊松比为依据时,高熵合金Al2CoCrCuFeNi为韧性材料,其余为脆性材料;以剪切模量与体积弹性模量的比值为依据时,高熵合金Al1.5CoCrCuFeNi和Al2CoCrCuFeNi可视为韧性材料,其余为脆性材料;3、在本文的计算条件下高熵合金AlxCoCrCuFeNi可视为热力学稳定的,随着Al元素摩尔含量的增大,高熵合金AlxCoCr-CuFeNi的生成热也随之增大.
[1] Ranganathan S.Alloyed pleasures:multimetallic cocktails[J].Current Science,2003,85:1404.
[2] Yeh J W,Chen S K,Lin S J,et al.Nanostructured high-entropy alloys with multiple principal elements:novel alloy design concepts and outcomes[J].Advanced Engineering Materials,2004,6(5):299.
[3] Huang P K,Yeh J W,Shun T T.Multi-principal-el-ement alloys with improved oxidation and wear resistance for thermal spray coating[J].Advanced Engineering Materials,2004,6(1-2):74.
[4] Yeh J W,Chen S K,Gan J Y.Formation of simple crystal structures in Cu-Co-Ni-Cr-Al-Fe-Ti-V alloys with multiprincipal metallic elements[J].Metallurgical and Materials Transaction,2004,35:2533.
[5] Hsu C Y,Yeh J W,Chen S K.Wear resistance and high-temperature compression strength of fcc Cu-CoNiCrAl0.5Fe alloy with boron addition[J].Metallurgical and Materials Transaction,2004,35:1465.
[6] Tong C J,Chen Y L,Chen S K,et al.Microstructure characterization of the AlxCoCrCuFeNi Highentropy alloy system with multiprincipal elements[J].Metallurgical Materials Transaction,2005,36:881.
[7] Tong C J,Chen M R,Chen S K,et al.Mechanical performance of the AlxCoCrCuFeNi high-entropy alloy system with multiprincipal elements[J].Metallurgical Materials Transaction,2005,36:1263.
[8] Wu J M,Lin S J,Yeh J W,et al.Adhesive wear behavior of Al xCoCrCuFeNi high-entropy alloys as a function of aluminum content[J].Wear,2006,261(5-6):513.
[9] Tung C C,Yeh J W,Shun T S,et al.On the elemental effect of AlCoCrCuFeNi high-entropy alloy system[J].Materials Letters,2007,61(1):1.
[10] Zhang Y,Peng W J.Micorstructural control and properties optimization of high-entrop alloys[J].Procedia Engineering,2012,27:1169.
[11] Yang X,Zhang Y,Liaw P K.Microstructure and Compressive Properties of NbTiVTaAlxHigh En-tropy Alloys [J].Procedia Engineering,2012,36:292.
[12] Liu L,Zhu J B,Zhang C,et al.Microstructure and the properties of FeCoCuNiSnxhigh entropy alloys[J].Materials Science and Engineering:A,2012,548:64.
[13] Takeuchi A,Chen N,Wada T,et al.Microstructure and Compressive Properties of NbTiVTaAlxHigh Entropy Alloys[J].Procedia Engineering,2012,36:226.
[14] Zhang K B,Fu Z Y,Zhang J Y,et al.Annealing on the structure and properties evolution of the CoCrFeNiCuAl high-entropy alloy[J].Journal of Alloys and Compounds,2010,502(2):295.
[15] Singh S,Wanderka N,Murty B S,et al.Decomposition in multi-component AlCoCrCuFeNi high-entropy alloy[J].Acta Materialia,2011,59(1):182.
[16] Mariela F G,Guillermo B,Hugo O M.Determination of the transition to the high entropy regime for alloys of refractory elements[J].Journal of Alloys and Compounds,2012,534:25.
[17] Wang W R,Wang W L,Wang S C,et al.Effects of Al addition on the microstructure and mechanical property of AlxCoCrFeNi high-entropy alloys[J].Intermetallics,2012,26:44.
[18] Senkov O N,Scott J M,Senkova S V,et al.Microstructure and room temperature properties of a high-entropy TaNbHfZrTi alloy [J].Journal of Alloys and Compounds,2011,509(20):6043.
[19] Shi D M,Wen B,Roderick M,et al.First-principles studies of Al-Ni intermetallic compounds[J].Journal of Solid State Chemistry,2009,182:2664.
[20] Zhou Y,Wen B,Ma Y Q,et al.First-principles studies of Ni-Ta intermetallic compounds [J].Journal of Solid State Chemistry,2012,187:211.
[21] Yang Z W,Shi D M,Wen B,et al.Structural,elastic,electronic properties and heats of formation of Ca-Zn intermetallics from first principles calculations[J].Journal of Alloys and Compounds,2012,524:53.
[22] Segall M D,Lindan J D,Probert M J,et al.First-principles simulation:idea,illustrations and the CASTEP code[J].Journal of Physics Condensed Matter,2002,14(11):2717.
[23] Ramer N J,Rappe A M.Application of a new virtual crystal approach for the study of disordered perovskites[J].Journal of Physics and Chemistry Solids.,2000,61(2):315.
[24] Bellaiche L,Vanderbilt D.Virtual crystal approximation revisited:Application to dielectric and piezoelectric properties of perovskites [J].Phys.Rev.B,2000,61(12):7877.
[25] Winkler B,Pickard C,Milman V.Applicability of a quantum mechanical‘virtual crystal approximation’to study Al/Si-disorder[J].Chemical Physics Letters,2002,362(3-4):266.
[26] Payne M C,Teter M P,Allan D C,et al.Iterative minimization techniques for ab initio total-energy calculations:molecular dynamics and conjugate gradients[J].Reviews of Modern Physics,1992,64(4):1045.
[27] Perdew J P,Burke K,Ernzerhof M.Generalized Gradient Approximation Made Simple[J].Physical Review Letters,1996,77(18):3865.
[28] Hamann D R,Schluter M,Chiang C.Norm-conserving pseudopotentials[J].Physical Review Letters,1979,43(20):1494.
[29] Leung T C,Chan C T,Harmon B N.Ground-state properties of Fe,Co,Ni,and their monoxides:Results of the generalized gradient approximation[J].Phys.Rev.B,1991,44(7):2923.
[30] Nye J F.Physical Properties of Crystals [M].Oxford:Oxford University Press,1985.
[31] Anderson O L.A simplified method for calculating the Debye temperature from elastic constants[J].Journal of Physics and Chemistry Solids,1963,24(7):909.
[32] Frantsevich I N.Voronov F F,Boduta S A.Elastic constants and elastic moduli of metals and insulators handbook[M].Kiev,1983:60.
[33] Pugh S F.XCⅡ.Relations between the elastic moduli and the plastic properties of polycrystalline pure metals[J].Philosophical Magazine:Series 7,1954,45(367):823.
