不同本构模型对船冰相互作用的影响

翟帅帅，李 辉，王 川，王金峰

(哈尔滨工程大学船舶与海洋工程力学研究所，黑龙江哈尔滨150001)

不同本构模型对船冰相互作用的影响

翟帅帅，李 辉，王 川，王金峰

(哈尔滨工程大学船舶与海洋工程力学研究所，黑龙江哈尔滨150001)

由于对物理模型做了大量假设，经验公式在计算船冰碰撞过程中的冰力时存在很多缺点，而且因为没有考虑船舶自身的非线性现象，导致计算结果与真实值存在较大误差。随着有限元技术的发展，使得利用有限元技术模拟海冰与船舶碰撞问题成为可能。海冰本构模型是影响船冰碰撞过程中计算精度的最重要因素，利用MSC．DYTRAN强大的非线性计算功能对海冰的弹塑性模型、弹脆性模型以及Derradji－Aouat多重失效面模型进行模拟，并且对计算结果和相关本构模型进行分析，认为基于应变率和温度并且考虑了静水压力对海冰失效的影响的多重失效面准则更加适合计算高应变率作用下的船冰碰撞问题。

海冰;本构模型;船舶;数值模拟;碰撞

0 引言

对于作业在有海冰漂浮海域的钻井平台或者航行于冰区的船舶来说，能够准确预报作用于海洋结构物上的冰力显得至关重要。随着我国对极地地区研究的不断深入，对船舶的抗冰性能和破冰性能提出了更高的要求。然而，由于船冰碰撞过程中，海冰表现出复杂的力学行为，并且随着应变率的不同表现出不同的屈服和断裂模式，传统的屈服准则并不能很好地模拟海冰的失效，虽然有些学者根据以往所做的海冰实验提出一些海冰本构模型［1－2］，然而其应用于船冰碰撞过程中的可靠性还有待研究。

在船冰碰撞的数值模拟中，海冰的本构模型对碰撞计算结果的影响最大，将直接导致模拟结果的精度。因此国内外很多学者对海冰的力学行为进行了大量的理论［3－5］和实验研究［6－9］，并且提出一些用于预测作用于海洋结构物的冰力计算公式，然而由于这些经验或者半经验公式做了很多假设和对物理模型的简化，因此，这些经验公式在计算超尺度的海洋结构物以及高应变率下的船冰碰撞问题时存在较大误差，而且这些经验公式并未考虑船冰碰撞过程中比如船体外壳的大变形等非线性因素的影响，因此在用经验公式预测碰撞力时要慎之又慎。

随着计算机技术的迅猛发展，借助有限元、离散元、边界元等方法来计算具有高度非线性的船冰碰撞问题成为可能。基于有限元法发展起来的诸如MSC．DYTRAN、LS．DYNA等商业软件能很好地模拟碰撞过程的强非线性和大变形现象。另外利用有限元技术对船冰碰撞问题进行数值模拟的好处有：一是模拟过程成本较低，而且能够看出经验公式在计算冰力时存在的一些本质问题;二是可以研究不同参数变化包括边界条件、海冰形式、冰排厚度等对计算结果的影响;三是通过数值模拟结果与实验结果的相互比照能够建立较为准确的海冰本构模型以达到预测相似冰况下的海冰与结构物相互作用现象。因此，本文将借助MSC．DYTRAN在分析结构及流体材料的非线性动态行为方面的强大功能，研究不同的海冰本构模型对船冰碰撞过程中碰撞力的影响，并且对不同的本构模型进行对比分析，指出不同本构模型的优缺点。

1 海冰力学性能

一般来说，海冰是不均匀、各向异性及非线性粘性材料。海冰的力学性能随着应变率的不同表现出不同的破坏模式，而且冰粒尺寸的不同对海冰的力学性能也有较大影响。本文研究的对象是高应变率 (一般认为应变率＞10－3s－1)下的柱状头年冰。海冰力学行为随应变率的变化曲线如图1所示。从图中可以看出，高应变率下的海冰行为类似于具有脆性破坏的线弹性材料。对于横观各项同性的柱状海冰来说，其弹性模量、泊松比、单轴拉压强度、剪切强度和弯曲强度与海冰的结晶方向、孔隙率、卤水体积等因素相关。

1.1 弹性模量和泊松比

图1 应变率对海冰力学行为的影响［6］Fig.1 The effect of strain rate on ice behavior

实验表明，弹性模量有较大的变化区间，而且静态测量值和动态测量值也存在较大不同。Bjornar Sand［10］通过总结前人的实验指出，静态测量的弹性模量在0.3～10 GPa之间，而动态测量值在6～10 GPa之间，静态测量值比动态测量值要小一些。对于横观各项同性 (Z轴平行于圆柱轴，X，Y轴垂直于圆柱轴，XY平面表现为各项同性)的海冰来说，其弹性模量的大小与结晶方向有关，EZ，EX和EY不同。另外，应变率也是影响弹性模量的重要因素，Kuehn［11］分别对应变率为 10－3s－1和 10－7s－1的实验室盐水冰做了拉伸试验，发现对应上述应变率下的X向弹性模量分别为 Ex=6.00 GPa和 Ex=1.83 GPa，而Z向弹性模量分别为Ez=8.19 GPa和Ez=5.33 GPa，弹性模量随着应变率的增加而增大。

泊松比与应变率、温度和结晶方向有关，一般借助试验的方法确定泊松比的大小。但需要注意，如果试验过程中蠕变成为主要变形因素，则认为此时的泊松比值是不准确的［12］。一般来说泊松比的取值为0.33。

图2 柱状海冰的坐标定义Fig.2 Definition of coordinate system of columnar sea ice

1.2 单轴拉压强度

海冰的拉压强度直接影响船冰碰撞过程中作用在船体外板上的作用力，因此深入理解海冰的拉压特性非常有必要。海冰的压缩强度与应变率、温度、孔隙率、加载方向等因素有关。有实验表明，在低应变率、高温度时海冰的抗压强度低至0.5 MPa;而高应变率、低温度时却高至大约12 MPa。另外，侧限压力的大小影响海冰的破坏形式，从而影响海冰的抗压强度。没有侧限压力时柱状海冰沿轴向开裂，而有侧限压力时海冰发生层裂。实验表明，Z向压缩强度大约是X向压缩强度的4倍。

实验表明，海冰具有SD效应 (压缩和拉伸屈服强度不等对塑形屈服的影响)，其抗拉强度远远小于抗压强度，在海洋结构物上加装锥形结构，可将海冰的破坏模式变为拉伸破坏，实地试验测量［13］表明，此种结构形式大大改善了结构的抗冰性能。虽然拉伸强度受到温度、卤水体积、晶粒大小的影响，但是其影响没有抗压强度明显，相比来说结晶方向对抗拉强度影响较大。实验表明Z向拉伸强度大约是X向拉伸强度的2～4倍。

1.3 剪切强度

目前讨论剪切强度的文献不多，现有的文献指出，海冰的剪切强度与温度、盐度、密度和加载方向相关。很多因素导致剪切强度难以测量，其中一个主要问题就是实验过程中不仅会产生剪切应力，而且在剪切平面上也产生正应力，因此导致测量结果不准确。

1.4 弯曲强度

解析方法在解决海冰与海洋结构物的问题中，海冰弯曲强度是很重要的考量因素。通常海冰的抗弯强度通过三点或四点弯曲试验来确定，试验结果表明，淡水冰的抗弯强度在0.5～1.0 MPa之间，而海冰在0.1～0.8 MPa之间。不过由于海冰的抗拉强度较小，拉伸断裂在弯曲试验中占主导地位，因为拉伸强度主要受加载率的影响，因此可以认为弯曲强度也主要依赖于加载率的大小。

2 本构模型

在用MSC.DYTRAN进行非线性瞬态动力分析时，不管材料模式多么复杂，单元精度多么高，最终结果的准确度还是要取决于材料本构模型参数的准确度［14］。虽然MSC.DYTRAN中已经提供了丰富的材料模型，但是并没有一种材料是专门基于海冰的力学行为提出的，因此在模拟过程中势必要选择一种海冰的近似材料，并且借助MSC.DYTRAN提供的用户子程序功能实现软件自身不具备的屈服破坏准则。

何菲菲［15］利用弹塑性模型对冲撞式破冰进行了数值模拟初探。武文华［16］利用 Ralston［3］提出的抛物线模型模拟了渤海海冰与JZ20海域海洋平台相互作用的过程。Derradji-Aouat［17］提出了多重失效面的海冰失效准则，并且成功将其应用在水电站［18］的数值模拟中。

2.1 弹塑性本构模型

本文采用的弹塑性模型是建立在单一屈服面方程上的von Mises屈服准则，根据传统塑性理论，屈服面不是破坏面，而失效准则需要以最大应力或者最大塑性应变来定义。在本文中当等效应力σ=10 MPa时，海冰开始发生塑形变形，定义最大塑性应变ε≥0.001时海冰失效。

其中 σ1，σ2，σ3为主应力。

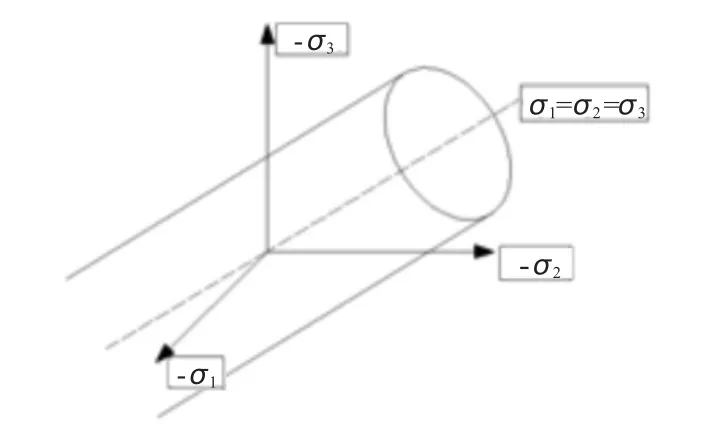
图3 Von Mises失效面包络线Fig.3 Failure envelop of von Mises modeling

2.2 弹脆性模型

对于船冰碰撞的高应变率问题，海冰表现出类似具有脆性破坏的线弹性材料。对于弹脆性材料来说，其屈服面与破坏面保持一致，考虑到柱状海冰的横观各项同性特点以及碰撞过程中海冰主要发生压缩破坏，因此本文选取MSC.DYTRAN中提供的正交各向异性材料，并且以最大压力P=10 MPa作为失效准则。

其中

式中：T为材料坐标系与基本坐标系之间的变换矩阵;CL为材料坐标系中的本构矩阵。

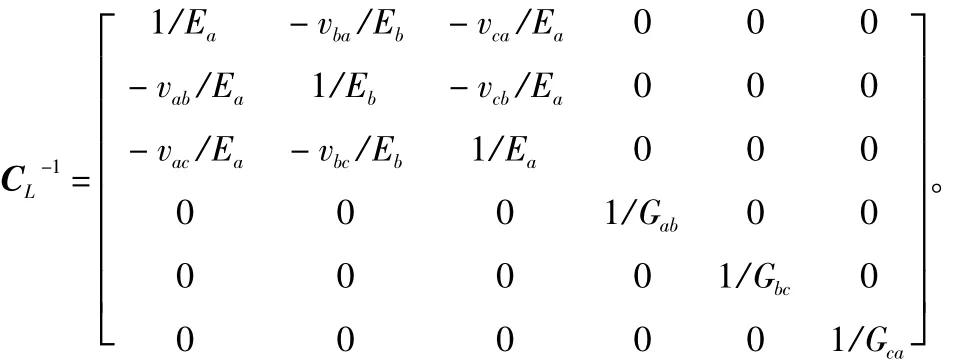
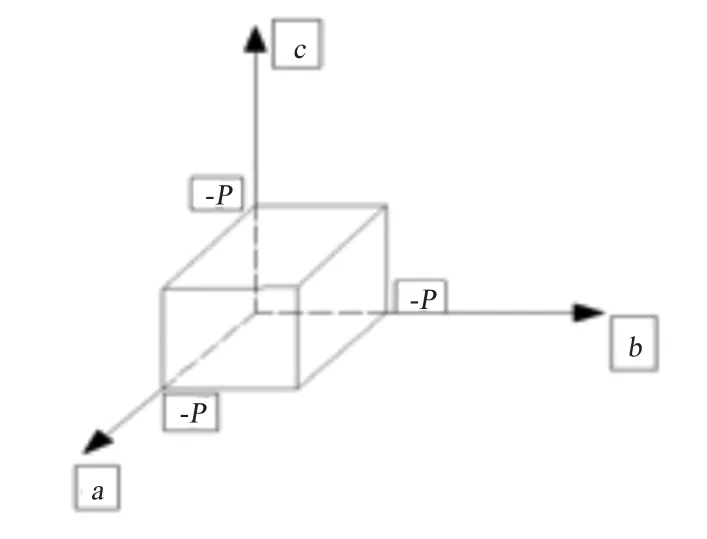
图4 弹脆性本构模型失效面包络线 (a，b，c是单元的拓扑学坐标系)Fig.4 Failure envelop of elastic-brittle modeling(a，b，c is the material coordinate system)

2.3 Derradji-Aouat多重失效面模型

Derradji-Aouat在总结前人的实验数据时发现，海冰的破坏很大程度上依赖于应变率、温度和侧限压力的变化。于是为更准确地反映上述因素的影响，他在Mroz的多重失效面理论基础上提出了适用于淡水冰、冰山冰和盐水冰的海冰失效模式，并且认为，3－D失效面模型也适用于柱状海冰的失效。

式中：J2D为应力偏量第二不变量;I2为应力张量第二不变量;I1为应力张量第一不变量。

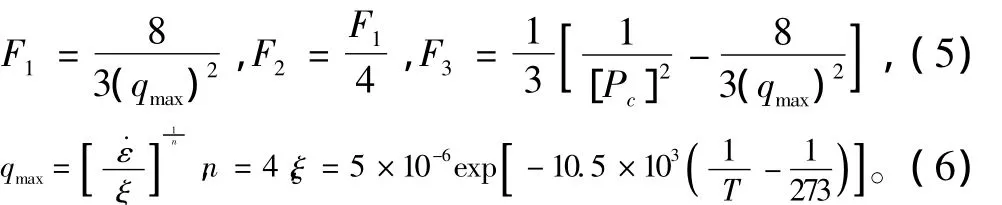
Pc=45.0 MPa(海冰)，55.0 MPa(淡水冰)。

Derradji-Aouat多重失效面模型的包络线如图5所示。

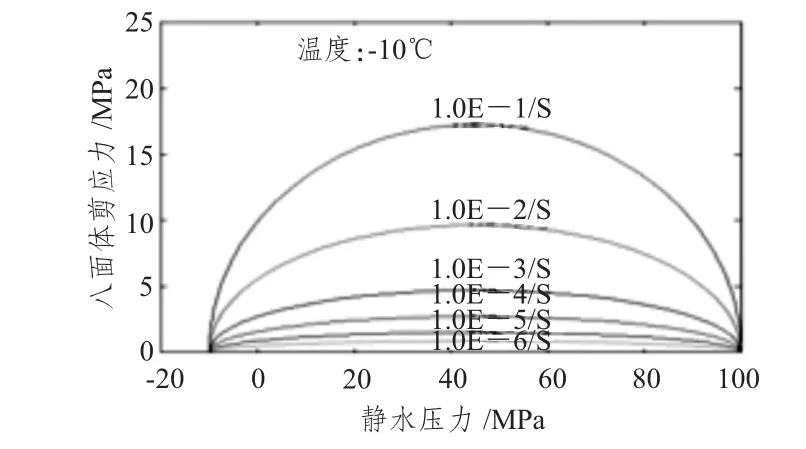
图5 失效面形状随应变率的形状变化Fig.5 Expansion of the failure envelope as the strain rate increases

本文将研究上述3种失效准则在用 MSC．DYTRAN对冲撞式破冰进行模拟时相互之间在碰撞力上的差异性，并且就计算结果进行分析讨论。

3 数值模型的建立

虽然将船体外壳简化为刚体会大大提高计算的效率，但是这样的假设没有考虑在冲撞式破冰过程中外壳板可能发生的大变形情况。因此为更好地反映船冰碰撞的实际情况，本文将船体可能发生碰撞的区域进行了精细建模，范围约为全船的前1/3区域，采用shell单元模拟。为模拟船体运动的正常浮态，船体后2/3区域用刚性外壳模拟，并且保证每一站的重量重心与实船相同。海水用欧拉网格进行模拟，在建立耦合面时，需要将船体后2/3区域的甲板用哑元闭合，哑元在计算过程中不参与计算，因此对其形状没有要求，哑元节点位置在整个计算过程中是不变的，因此需要避免因为因模型移动和变形造成负体积而导致计算终止［14］。海冰用八节点六面体单元模拟，用非线性弹簧元模拟海水的浮力作用，其计算公式如图6所示。

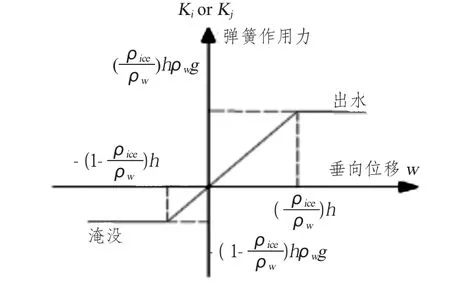
图6 海冰非线性弹簧力计算示意图Fig.6 Spring force versus vertical displacement

建立的船冰碰撞模型如图7所示，共有15 744个shell单元，76 800个欧拉体单元，46 380个拉格朗日体单元，26 938个一维弹簧元，有限元模型如图7所示。船体前端距离海冰边缘约20 m距离，是为了保证船体在与海冰发生碰撞时具有正常浮态。从速度曲线中可看出，船体在开始时有较大的垂向位移;从接触力的曲线看出，在4.8 s左右时船冰开始发生碰撞，此时船体已经有正常的浮态。本文将模拟船舶以8 kn初始速度与2 m厚海冰发生碰撞的过程，除碰撞一侧外，冰排的其余三边刚性固定，计算时间13 s，用16核64 GB内存的工作站需要计算50～60 h。本文计算的4种海冰本构模型设置参数如表1所示。

图7 船冰有限元模型图Fig.7 Ship and sea ice finite element model

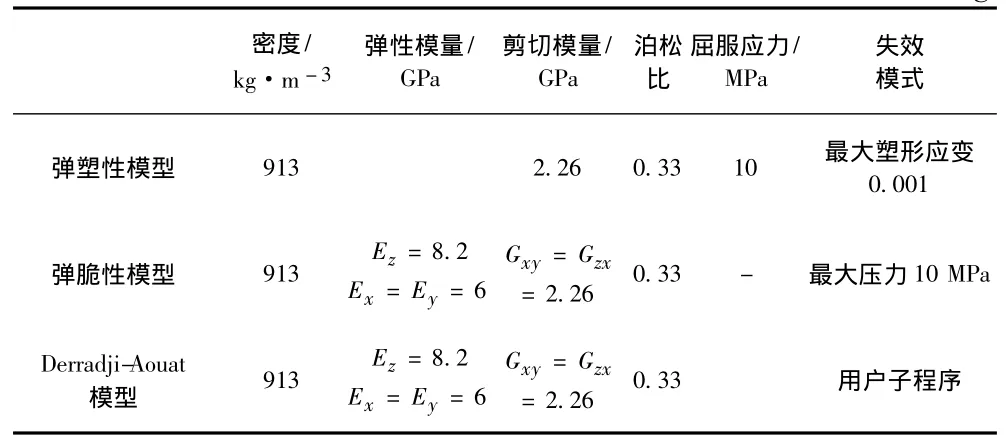
表1 三种海冰本构模型的设置参数Tab.1 Parameter value of the three above constitutive modeling

4 数值模拟结果及分析

4.1 碰撞力数值模拟结果

碰撞力的大小直接决定船体结构的设计和预报破冰船的破冰能力，因此本文将着重比较3种本构模型之间碰撞力的差异，并且从本构模型本身分析造成差异的原因。

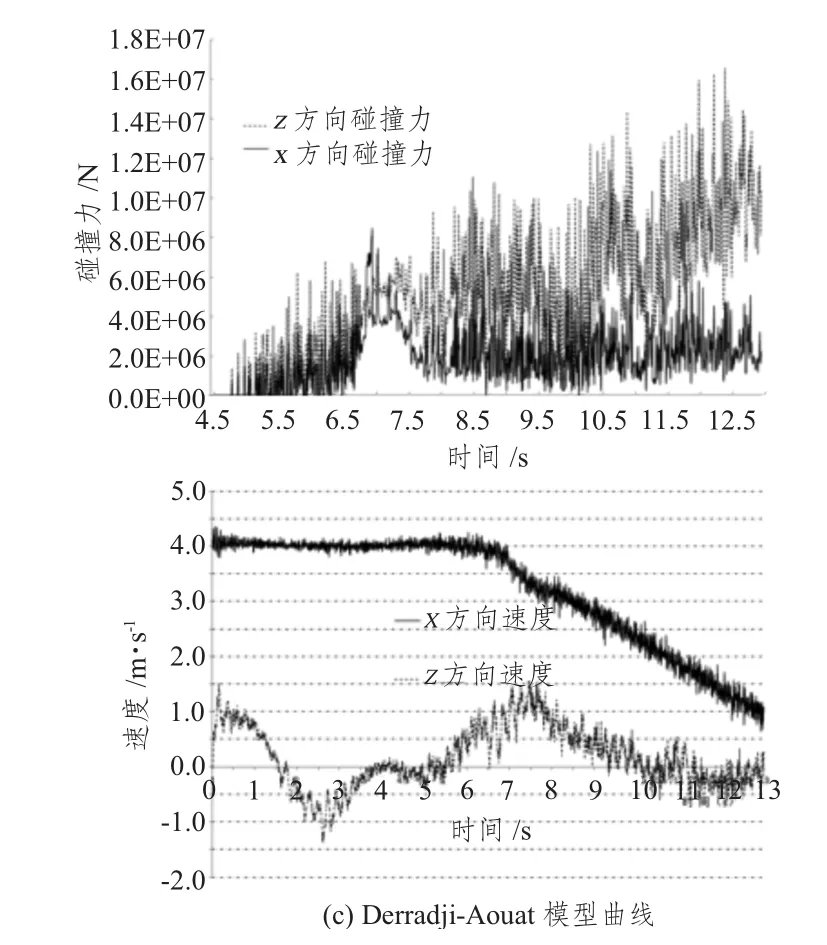
图8 X，Z方向碰撞力和船体速度时域曲线Fig.8 The curves of horizontal and vertical crash forces and velocities

4.2 碰撞力响应分析

从上述碰撞力和速度曲线可以看出以下3点：1)z方向的碰撞力约为x方向的2倍，这是由船体外形决定的;2)船体在重力、浮力和z方向碰撞力的作用下上下波动;3)x方向的碰撞力决定了破冰船的破冰能力，从图中可以看出不同的失效准则对预测船体的破冰能力有着决定性的作用。因此本文将结合x方向碰撞力和速度曲线重点分析3种本构模型的适用性。

弹塑性模型是基于传统塑形屈服理论得到的。从碰撞力曲线可以看出，随着撞深增加碰撞力持续增大，而且由于以最大塑形应变为失效准则，因此只有与船体相接触的单元发生失效，并未出现冰排的径向或者环向断裂，而且单元的失效时刻严重依赖于最大塑形应变的设置，从而大大影响碰撞力的变化。另外，弹塑性模型并未考虑海冰拉压强度之间的差别，也未考虑静水压力的影响，因此传统的弹塑性模型只能粗略模拟船冰碰撞过程。

弹脆性模型主要考虑船冰碰撞过程海冰发生的压碎现象，但是船体外壳并非直立结构，碰撞过程中很多单元的失效是由拉应力决定的，发生的是拉伸、弯曲、剪切破坏，而非压缩破坏。从碰撞力曲线也可看出，以压缩强度作为海冰的破坏准则并不能正确反映碰撞力的大小和速度的变化规律，因此以单轴压缩强度作为海冰的失效准则会大大高估海冰的抵抗能力，使得船体设计过分保守。

Derradji-Aouat基于实验数据提出的海冰失效模型一方面考虑了应变率、静水压力、温度在海冰破坏中的影响;另一方面也考虑了海冰拉压强度不同的SD效应，此模型已成功应用到海冰和水电站挤压断裂过程的数值模拟中［18］。但 Derradji-Aouat模型需要确定的参数较多，而且不同的海域有着特定的参数设置，因此在将此模型应用于特定冰区时还需进行大量实验以确定相关参数。

5 结语

本文通过将目前在数值模拟中常用的3种海冰本构关系引入到船冰碰撞问题中发现，传统的弹塑性模型虽然不能很好地模拟船冰碰撞过程，但在船舶设计初期还是可以利用其简单性来粗略预测破冰船的破冰能力和结构安全性。Derradji-Aouat模型能够很好地模拟高应变率下的船冰碰撞问题，但其需要确定的参数较多，而且并未细致考虑远离碰撞区域的海冰低应变率力学行为，因此还需完善。

［1］ZENG L F，ANDERSEN R．Modelling ductile behavior of columnar ice using conputational plasticity ［J］．Proceedings of the 12th IAHR Symposium on Ice，1994(1)：282－291．

［2］DERRADJI-AOUAT A．Multi-surface failure criterion for saline ice in the brittle regime［J］．Cold Regions Science and Technology，2003，36：47 －70．

［3］RALSTON T D．An analysis of ice sheet indentation［J］．Proceedings of the IAHR Symposium on Ice，1978：13 －31．

［4］MICHEL B，TOUSSAINT N．Mechanisms and theory of indentation of plates［J］．Journal of Glaciology，1977，19(81)：285－301．

［5］李锋，岳前进．不同破坏模式下锥体结构冰力定性分析［J］．大连理工大学学报，2005，45(6)：785 －788．

LI Feng，YUE Qian-jin．Qualitative analysis of ice forces on conical structures under different failure modes［J］．Journal of Dalian University of Technology，2005，45(6)：785－788．

［6］SCHULSON E M．Brittle failure of Ice［J］．Engineering Fracture Mechanics，2001，68：1839 －1887．

［7］JONES S J．The confined compressive strength of polycrystalline Ice［J］．Journal of Glaciology，1982，28(98)：171－177．

［8］沈梧，林树枝．渤海东部一年冰单轴压缩强度的应变速率敏感性［J］．大连工学院学报，1984，23(4)：45 －50．

SHEN Wu，LIN Shu-zhi．The strain rate sensitivity of strength ofBohaisea one yearice underuniaxial compression［J］．Journal of Dalian University of Technology，1984，23(4)：45 －50．

［9］孟广琳，张明远，李志军．渤海平整冰单轴抗压强度的研究［J］．冰川冻土，1987，9(4)：329 －338．

MENG Guang-lin，ZHANG Ming-yuan，LI Zhi-jun．Study of the uniaxial compressive strength of the Bohai sea ice［J］．Journal of Glaciology and Geocryology，1987，9(4)：329－338．

［10］SAND B．Nonlinear finite element simulations of ice forces on offshore structures［M］．University of Technology，2008．

［11］KUEHN G A，LEE R W，NIXON W A，et al．The structure and tensile behavior of first-year sea ice and laboratorygrown saline ice［J］．Journal of Offshore Mechanics and Arctic Engineering，1990，112：357 －363．

［12］SANDERSON T J．Ice mechanics-risks to offshore structures［M］．London：Graham ＆ Trotman，1988．

［13］屈衍．基于现场实验的海洋结构随机冰荷载分析［D］．大连：大连理工大学，2006．

QU Yan．Random ice load analysis on offshore struetures based on field tests［D］．Dalian：Dalian University of Technology，2006．

［14］丁沛然，钱纯．非线性瞬态动力学分析：MSC．DYTRAN理论及应用［M］．北京：科学出版社，2006．

DING Pei-ran，QIAN Chun．Non-linear transient dynamic analysis：MSC．DYTRAN theory and application［M］．Beijing：Sciences Press，2006．

［15］何菲菲．破冰船破冰载荷与破冰能力计算方法研究［D］．哈尔滨：哈尔滨工程大学，2011．

HE Fei-fei．A computational method for ice-breaking loads and ice-breaking capability of icebreaker［D］．Harbin：Harbin Engineering University，2011．

［16］武文华，于佰杰，许宁．海冰与锥体抗冰结构动力作用的数值模拟［J］．工程力学，2008，25(11)：192 －196．

WU Wen-hua，YU Bai-jie，XU Ning．Numerical simulation of dynamic ice action on conical structure［J］．Engneering Mechanics，2008，25(11)：192 －196．

［17］Derradji-Aouat Ahmed．Multi-surface failure criterion for saline ice in the brittle regime［J］．Cold Regions Science and Technology，2003，36(1 －3)：47 －70．

［18］DERRADJI-AOUAT A，LAU M．Ice loads on electric power generating stations in the belle isle strait［J］．18th Int．Conf．on Port and Ocean Eng．Under Arctic Conditions，2005(1)：387－398．

The effect of different constitutive modeling on ship-ice interaction

ZHAI Shuai-shuai，LI Hui，WANG Chuan，WANG Jin-feng
(Institute of Naval Architecture and Ocean Engineering Mechanics，Harbin Engineering University，Harbin 150001，China)

Because of a mass of assumes，there are a lot of disadvantages using empirical formulations to calculate ice loads on ship-ice interaction．Besides，lost sight of the strong nonlinear phenomenon on ship hull，the validity of using existing ice load formulation is surrounded by very high level of uncertainty．The development of finite element method(FEM)made it possible to simulate ship-ice crashing phenomenon．Constitutive modeling of ice behavior plays the most important role in calculation．Numerical simulations of the elastic-plastic criterion，elastic-brittle criterion and Derradji-Aouat multisurface criterion were carried out by using MSC．DYTRAN．Based on the results，the advantages and disadvantages were analysed between different constitutive modeling．Considering the effect of strain rate，temperature and hydrostatic，multi-surface failure criterion is more suitable in numerical simulations of shipice interaction．

sea ice;constitutive modeling;ship;numerical simulation;crash

U661．943

A

1672－7649(2014)06－0020－06

10.3404/j.issn.1672－7649.2014.06.004

2013－08－23;

2013－09－29

国家自然科学基金资助项目(51109046);国家973发展基金资助项目(2011CB013703)

翟帅帅(1987－)，男，硕士研究生，主要从事破冰船载荷及强度研究。