船舶水动力性能的多目标优化方法

胡腾飞，王先洲，刘 平，张志国，冯大奎

(1．华中科技大学船舶与海洋工程学院，湖北武汉430074;2．中国人民解放军92537部队，北京100161)

船舶水动力性能的多目标优化方法

胡腾飞1，王先洲1，刘 平2，张志国1，冯大奎1

(1．华中科技大学船舶与海洋工程学院，湖北武汉430074;2．中国人民解放军92537部队，北京100161)

很多对船舶水动力性能的优化都是对单一性能进行研究，已经不适用于现代化的造船要求。本文对不同遗传算法和粒子群优化算法进行分析，探讨其在船舶水动力性能优化方面的作用，以DTMB5415为母型船进行优化，改变不同算法的参数设置观察优化结果，最后通过分析Pareto解得到最适用于本次研究的优化算法及其参数设置。

船舶水动力性能;多目标优化;遗传算法;粒子群优化算法

0 引言

船舶作为一个复杂的综合系统，其所涉及的学科领域众多。就水动力性能而言，可以划分为耐波性、快速性、操纵性等领域，各性能自身作为独立学科存在，同时又与其他性能相互关联、相互制约着。之前针对某一船型的优化，往往都是集中在某一学科领域［1－2］。由于各性能要素对船型参数的要求往往相互矛盾，因此，针对某一性能的改善可能同时也牺牲了其他性能。随着对船舶所承担的任务要求越来越高，单一作业性能已经不能满足未来发展需要，而多工况下对船舶的各个性能指标都提出了新的要求。

为了解决上述问题，在船舶设计中引入了“多目标优化 (Multi－objective Optimization)”的概念，其意义在于寻找一个或多个解，使得决策者能接受所有的目标值。李立君、崔连琼、李学斌等［1－4］研究了多目标遗传算法，以及基于多目标遗传算法的船体方面和航空发动机的性能优化应用。操安喜［5］采用基于遗传算法的协同优化方法，对某深海载人潜水器耐压球壳进行多目标优化设计，验证其稳定性和可靠性。Hyunyul Kim［6］利用一种多目标遗传算法来满足多目标设计的速度，然后计算与阻力相关的目标方程，从而优化船舶型线。Yusuke Tahara等［7］开发和示范了一种基于CFD的多目标船体优化设计方法，运用2种非线性优化算法对此进行研究，验证了方法的有效性。Boulougouris E K［8］提出一种多目标流体力学优化过程，即用遗传算法来找到Pareto最优解然后赋予权重选择其中的最优解。尽管多目标优化有了很大发展，但对适用于水面舰船水动力性能优化的优化算法的对比研究相对较少。本文将多种多目标优化算法应用到船舶水动力性能优化研究中，并改变各种优化算法的参数，由此寻求最适用于船舶水动力性能的多目标优化问题的优化算法及其参数设置。

1 理论基础

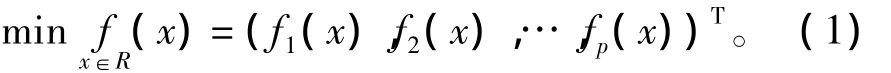
若x*∈R，且不存在 x∈ R，使得 fi(x)≤fi(x*)(i=1，2，…，p)，则x*为Pareto最优解。Pareto最优解集为：

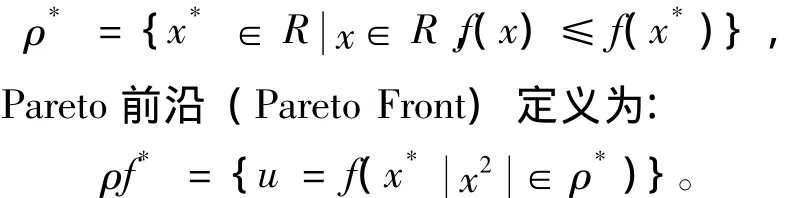
对于多目标问题：

图1 两目标优化的Pareto前沿及可行域Fig.1 Pareto Front and Feasible Region

图1所示为求解两目标优化得到的Pareto前沿及可行域，A，B，C分别分布于Pareto前沿的 (近似)的最优解，点D，E所在区域为基于目标的可行解区域，相对于点A，B，C，点D和E所表示的解为劣解。点A，B和C对应的Pareto前沿上的解均为Pareto最优解，对应的解集为Pareto最优解集。很明显，如果目标函数f1或f2或其中之一不变时，Pareto前沿上的值在可行域内最优。

1.1 多目标遗传算法

遗传算法［9］(Genetic Algorithm，GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。本文对多种改进的遗传算法进行研究，主要包括存档微遗传算法 (AMGA)，多岛遗传算法 (MIGA)，领域培植多目标遗传算法(NCGA)，第2代非劣排序遗传算法 (NSGAⅡ)。遗传算法的参数包括种群规模P(population size)，字串长度l(string length)，交叉概率pc(probability of performing crossover)，变异概率pm(probability of mutation)和中止条件 (termination criteria)。GA的一般流程图如图2所示。

图2 遗传算法一般流程图Fig.2 GA Flowchart

1.2 粒子群优化算法

粒 子 群 优 化 算 法［10］(Particle Swarm Optimization，PSO)，又称微粒群算法，来源于对一个简化社会模型的模拟。粒子群优化算法的流程图如图3所示。PSO算法参数一般包括群体规模m，惯性权重w，加速常数c1和c2，最大速度Vmax，最大代数Gmax。

图3 粒子群优化算法一般流程图Fig.3 PSO Flowchart

2 优化过程

2.1 算例证明

为了验证程序的正确性，对一个数学算例进行多目标优化，问题描述如下：

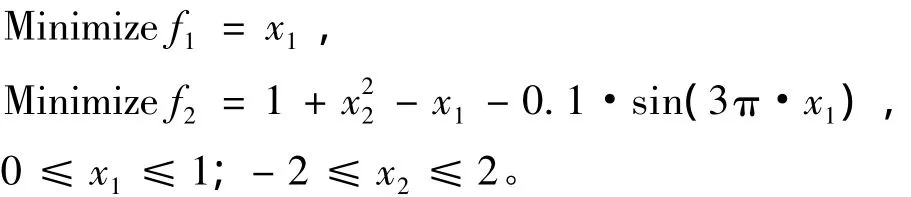
对此问题分别采用5种算法进行计算，下面列出一种遗传算法 (NSGAⅡ算法)的优化结果和粒子群优化算法 (PSO)的优化结果，Pareto解分布f1vs.f2如图4所示。

图4 算例优化结果Fig.4 Result of Example

通过图4可以发现此次优化是成功的，并且从图中可以很明显地观察到Pareto前沿 (最左边的点组成)，其中Pareto解都满足约束条件，此次优化收敛也说明该程序的有效性。对其余算法的结果进行分析可以得到同样的结论。

2.2 目标函数

本次研究考虑的船舶水动力性能包括快速性和耐波性。其中快速性主要考虑减小船舶的阻力系数ct。阻力的计算利用 Holtrop经验公式［11］，Holtrop阻力回归公式如下：

式中：RF为摩擦阻力;RAPP为附体阻力;RW为兴波阻力;RB为球首近水面附加压阻力;RTB为尾封板浸水附加压阻力;RA为船模相关压力;1+k1为船体粘性阻力形状因子。

耐波性评估采用N.K.Bales［12］提出的耐波性最优化模型，这个模型是通过对驱逐舰一类的排水式过度船型的深入研究，把反映耐波性能优劣程度的耐波性品级指标R和几个重要船型几何特征通过简明关系式直接联系起来。R的大小可以用于综合评价高速排水式船舶的耐波性。由于本文研究的船型为DTMB5415，所以可以采用此经验公式，如下：

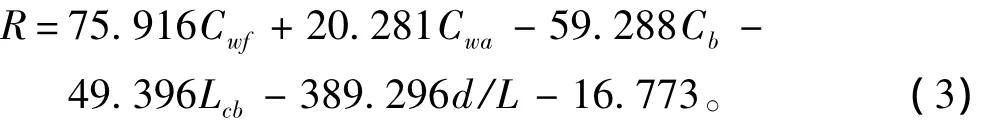
式中：Cwf和Cwa分别为前、后体水线面系数;d为吃水;L为水线长;Cb为方形系数;Lcb为浮心纵向位置。

综上所述，为了使得舰船阻力小的同时耐波性品级指标高，可以决定目标函烽为：

2.3 设计变量和约束条件

本文以DTMB5415［13］母型船为研究对象，确定部分计算常量如表1所示。为了计算方便与准确性，将原有的一些数值全部转化为无量纲数。所以设计变量和初值如表2所示。约束条件包括船舶主尺度的约束和数值自身物理含义的约束。

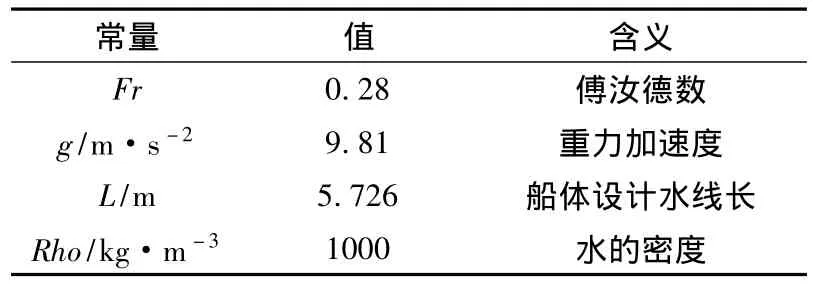
表1 常量Tab.1 Constant

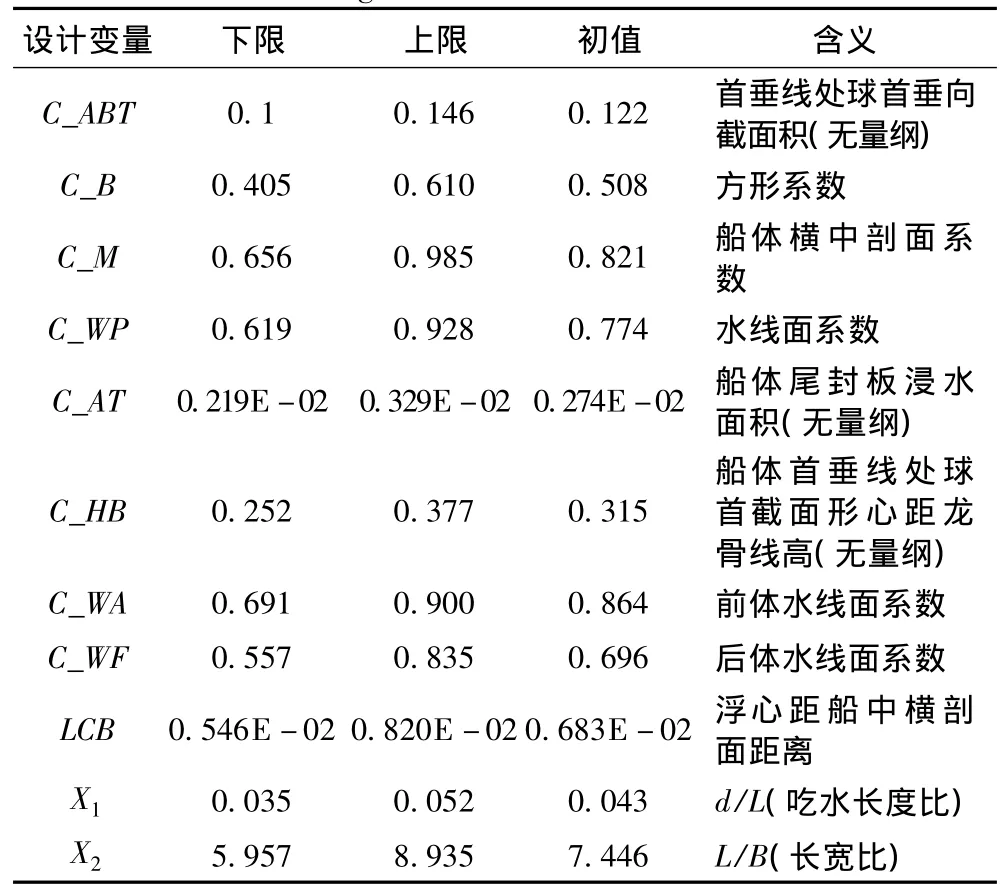
表2 设计变量和初值Tab.2 Design variables and the initial value

2.4 优化结果分析

本次研究采用5种不同的多目标优化算法，数学模型，约束条件和设计变量相同。不同的优化方法其参数的设置不一样，对结果也有一定的影响，所以对于每种优化方法，对其参数进行改变，然后观察优化结果，确定对于本次优化最有利的一种参数设置。

具体方法为在不改变评价总数的情况下改变其它参数，为了在优化过程中消除计算误差，每个Pareto解的个数都是计算10次取平均值得到的。具体结果如表3～表7所示。

表3 AMGA算法参数Tab.3 Main parameters of AMGA

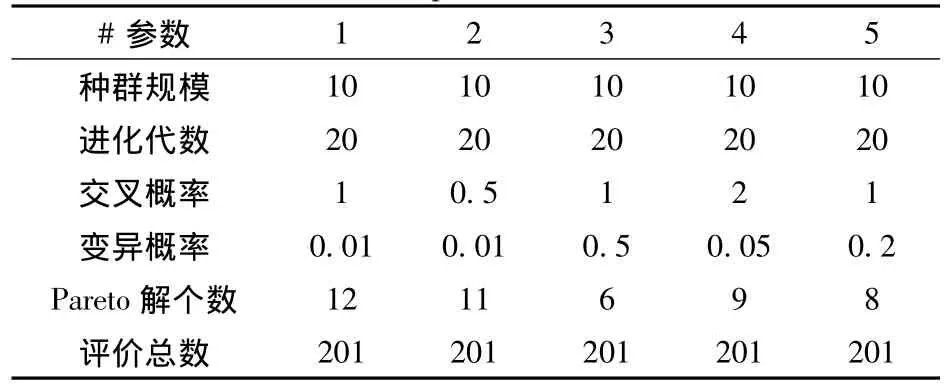
表4 NCGA算法参数Tab.4 Main parameters of NCGA

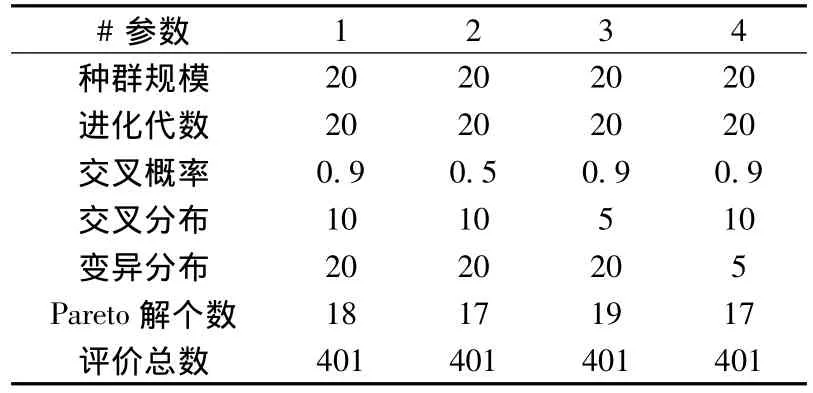
表5 NSGAⅡ算法参数Tab.5 Main parameters of NSGAⅡ

表6 MIGA算法参数Tab.6 Main parameters of MIGA

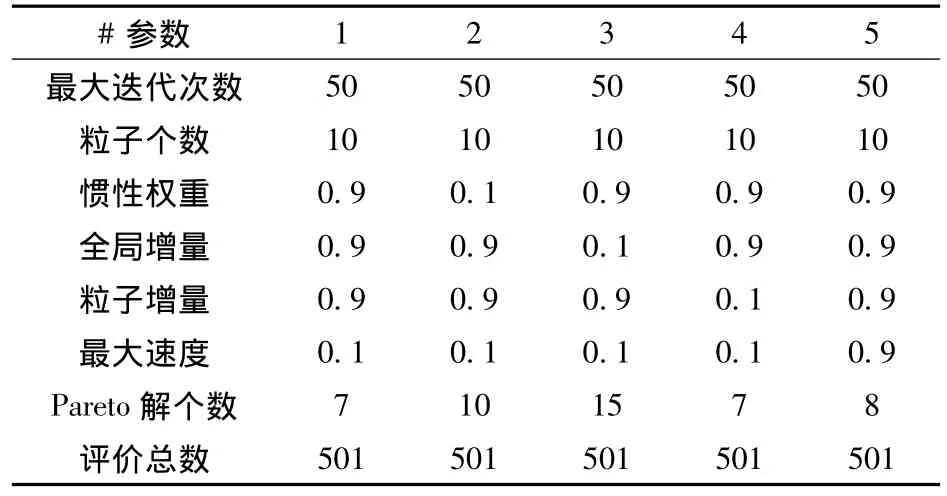
表7 PSO算法参数Tab.6 Main parameters of PSO

通过表中结果可以看出，本次优化中，对于AMGA而言，不改变评价总数时，改变部分参数对结果数量的影响不大，这是因为优化过程中存档和当代种群没有改变，在其搜索过程中得到的解集也不会有很大变化，但是当评价数量变化，例如表3第3列中，改变了初始规模和种群规模，得到的解的数量随着评价总数的减少而减少;对于NCGA，发现变异概率对结果的影响比较大，一般变异概率过高，会使遗传搜索变为随机搜索，本次优化中，通过对计算结果的分析，决定本次优化中，变异概率范围定在0.01～0.05;NSGAⅡ和MIGA算法进行优化时，参数的改变对结果影响不大，其原因是因为这2种改进的遗传算法，都比较适用于非连续的计算空间，对计算规模的要求比较大，在不改变评价总数时，各种参数的改变对总体搜索的改变很小，因此导致此次优化结果中的情况;PSO算法的计算结果表明大部分参数对结果有一定的影响，其中全局增量的影响比较大，最大速度的影响比较小。

在确定上述几种优化算法的最佳参数设置后，对其最好的优化结果进行比较，具体如表8所示，Pareto解分布如图5所示。

表8 不同算法结果比较Tab.8 Results of different optimization algorithm

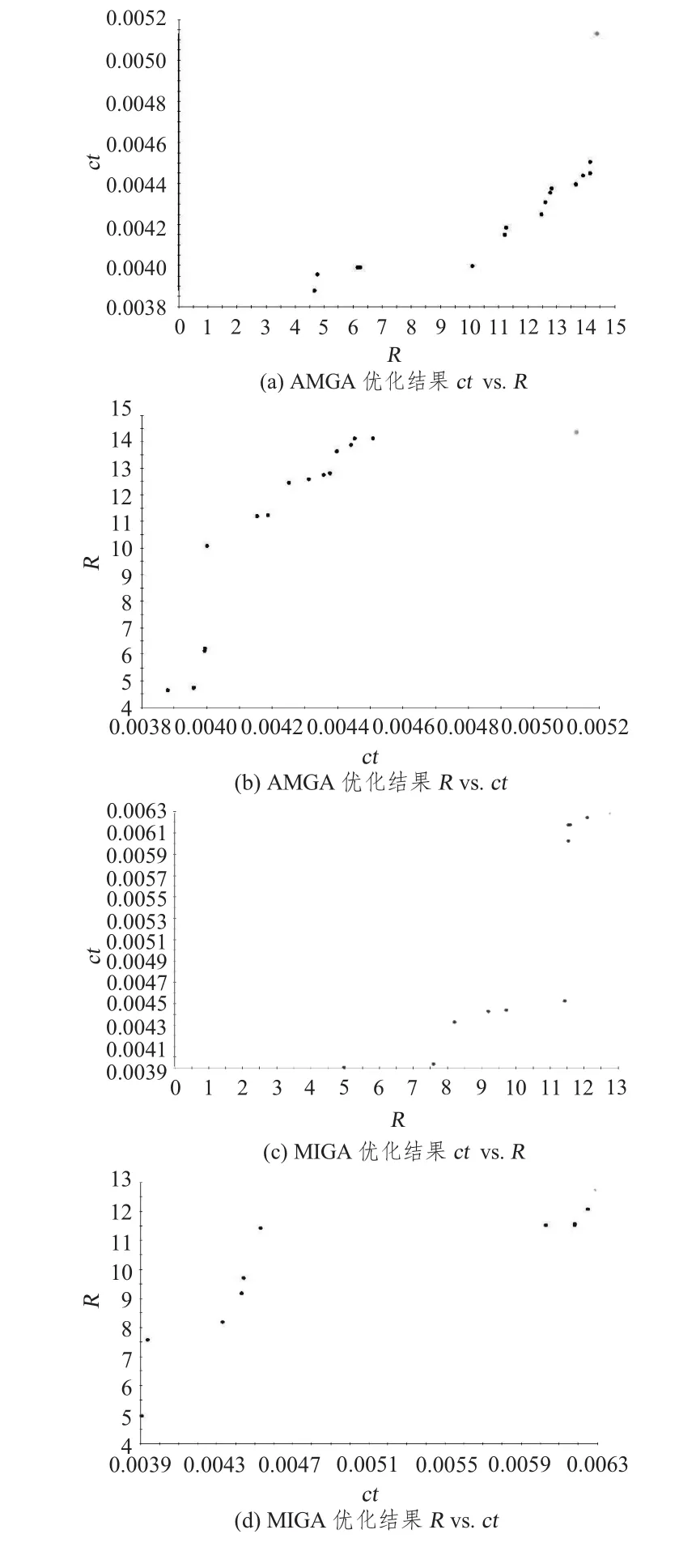
图5 不同优化方法Pareto解分布Fig.5 Pareto front of different optimization algorithm

从计算结果可以看出，对本问题，MIGA算法效率较低 (1个Pareto解需要66.7次评价)，Pareto解分布比较广，不在一个区域;NCGA虽然算法效率最高 (1个Pareto解需要16.8次评价)，但Pareto解不够连续;NSGAⅡ算法效率较高 (1个Pareto解需要22.3次评价)Pareto解也比较均匀连续;AMGA算法效率较低 (1个Pareto解需要29.5次评价)，Pareto解中段连续性不好;PSO算法效率也比较低 (1个 Pareto解需要33.4次评价)，但是其Pareto解分布很均匀，连续性也比较好，说明PSO算法的全局搜索能力更强。综合考虑算法效率和搜索能力，采用PSO算法对本问题进行优化比较好，能够得到更理想的优化结果。

3 结语

本文对船舶水动力性能进行多目标优化，同时考虑了水动力性能的快速性和耐波性2个方面，采用不同的优化算法均成功得到了Pareto解集。

对多目标优化算法的选择和参数的设置进行研究，分析几种常见的优化算法在此方面的应用，得到最适用于本次计算研究的多目标优化算法为PSO(粒子群优化算法)以及其参数设置，为以后对船舶水动力性能多目标优化提供了思路。

以本文为基础，还可以展开进一步的的探讨研究，比如加入船舶操纵性，或者采用高精度求解器对性能进行预报等。相信随着性能预报方法和优化算法的不断改进，利用多目标优化的手段对船舶性能的研究以及船舶的设计将更加细致和全面。

［1］李学斌．多目标遗传算法在船舶操纵性优化设计中的应用［J］．造船技术，2008，(4)：10 －12．

LI Xue-bin．Multi-objective evolutionary algorithm in the optimaldesign ofthe detailed-design［J］．Marine Technology，2008，(4)：10 －12．

［2］李学斌．多目标遗传算法在水面船舶快速性优化设计中的应用［J］．江苏科技大学学报(自然科学版)，2008．22(5)：1 －5．

LI Xue-bin．Application of multi-objective genetic algorithm to the optimal and fast design of surface ship［J］．Journal of Jiangsu University of Science and Technology(Natural Science Edition)，2008，22(5)：1 －5．

［3］李立君，尹泽勇．基于多目标遗传算法的航空发动机总体性能优化设计［J］．乔渭阳航空动力学报，2006(1)：13－18．

LI Li-jun，YIN Ze-yong．Performance optimal design of aircraft engine based on multi-objective genetic algorithms［J］．Journal of Aerospace Power，2006(1)：13 －18．

［4］崔连琼．多目标遗传算法及其在船舶型线优化中的应用［D］．武汉：武汉理工大学，2008．

CUI Lian-qiong．The studyofmulti-objective genetic algorithm and its application in ship design［D］．Wuhan：Wuhan University of Tecnology，2008．

［5］操安喜．载人潜水器多学科设计优化方法及其应用研究［D］．上海：上海交通大学，2008．

CAO An-xi．Multidisciplinary design optimization method and its application in HOV design［D］．Shanghai：Shanghai Jiao Tong University，2008．

［6］HYUNYUL K C Y．A new surface modification approach for CFD － based hull form previous optimization［J］．Journal of Hydrodynamics，2010(10)：520 －525．

［7］YUSUKETAHARA，YUSUKETAHARA S，TOHYAMA S，KATSUI T．CFD －based multi－objective optimization method for ship design［J］．International Journal for Numerical Methods in Fluids，2006，52：499 －527．

［8］E．K．;PAPANIKOLAOU，A．D．Multi-objective optimization of a floating LNG terminal Boulougouris［J］．Ocean engineering，2008，35(8 －9)：787 －811．

［9］HOLLAND J H．Adaptation in natural and artificial systems［M］．Ann Arbor：University of Michigan press，1975．

［10］JOHAN S．Managing inconsistent intelligence［C］．The third internationalconference ofInformation，Fusion．Sunnyvale，CA，2000．

［11］HOLTROP J，MENNEN G．G．J．A statistical power prediction method［J］．International Ship Build Progress，1978，25：253－256．

［12］BALES N K，CUMINS W E．The influence of hull form on seakeeping［J］．TSNAME，1970，78．

［13］OLIEIVRI A，PISTANI F，AVANZINI A，et al．Towing tank experiments of resistance，sinkage and trim，boundary layer，wake，and free surface flow around a naval combatant inseam 2340 model，IIHR Technical Report No．421［C］．IIHR-Hydroscience and Engineering college of Engineering，The University of Iowa，2001．

Investigation of multi-objective optimization on ship hydrodynamic performance

HU Teng-fei1，WANG Xian-zhou1，LIU Ping2，ZHANG Zhi-guo1，FENG Da-kui1
(1．School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China;2．No．92537 Unit of PLA，Beijing 100161，China)

There are several ways to optimize the ship resistance，seakeeping or the ship maneuverability in the last decades．However，most methods just take the only one performance into consideration and this is not suitable for the modern ship design and building．The paper analyzes the use of five multi-objective optimization algorithms such as archive-based micro genetic algorithm(AMGA)，multiisland genetic algorithm(MIGA)，neighborhood cultivation genetic algorithm(NCGA)，non-dominated sorting genetic algorithmⅡ (NSGAⅡ)and particle swarm optimization(PSO)in ship hydrodynamic performance，then finding the best method and its parameters based on DTMB5415．

ship hydrodynamic performance;multi-objective optimization;GA;PSO

U661．3

A

1672－7649(2014)06－0014－06

10.3404/j.issn.1672－7649.2014.06.003

2013－10－18;

2013－12－26

国家自然科学基金资助项目(51009070);国家863计划资助项目(2012AA091002)

胡腾飞(1989－)，男，硕士研究生，研究方向为船舶动力性能计算与优化。