搭建多元学习平台,助推“问题解决”策略性知识的形成——以“植树问题”教学为例
2014-07-10陈祖惠
陈祖惠
策略性知识是关于如何学习、如何思维的知识。让学生“学会学习、学会创造”的核心就是策略性知识。 在小学数学的教学中,有很多“问题解决”的内容,其主要目的不在于解决问题本身,而在于引导学生在解决该问题的过程中,反思、提炼、总结、发现其中的方法策略, 形成策略性知识, 从而达到举一反三、触类旁通、提高能力的目的。 为此,我认为,我们教师在教学中,为学生搭建多元学习平台,引导学生体验反思,可以助推“问题解决”策略性知识的形成。
一、多样化自主尝试,感知策略性知识
小学数学课程标准指出:“学生学习应当是一个生动活泼的、主动的和富有个性的过程,除接受学习外,动手实践、自主探索与合作交流也是数学学习的重要方式,学生应当有足够的时间和空间经历观察、实验、猜测、验证、推理、计算、证明等活动过程”。 因此, 教师在教学中要营造有利于学生自主学习的氛围,给学生搭建自主学习的平台,尊重学生的差异,提供多元化的学习方式, 引导学生在亲身经历自主探究的活动过程中体验学习,积累活动经验。自主是一种学习状态,学生唯有变被动为主动探究,才会激发学习潜能,形成学习能力,生成创造才能。
在《植树问题》的教学中,针对数学问题:“在全长100 米的小路一边植树,每隔5 米栽一棵(两端要栽),一共需要多少棵树苗?”刘杰老师根据学生已有的知识经验,充分相信学生的探究能力,出示问题后只给出三个开放性问题就放手学生进行独立的自主探究活动。 孩子们首先根据自己已有的生活和学习经验,用自己喜欢的方式尝试解决问题。 我们看到,有的学生用摆学具的策略;有的学生用画图的策略;有的学生用算的策略;还有的孩子用举例等策略。通过这样的自主尝试探究,学生对解决“植树问题”的策略性知识有了初步的感知。 正因为有了这样放手的自主探究尝试,有了自己的活动体验,才有后面精彩的交流和源自内心的对策略性知识深刻的感悟。
二、多向化互动交流,凸显策略性知识
小学数学课程标准指出:“数学活动是师生共同参与、交往互动的过程”。一个富有生命力的课堂,总是在动态中生成。课堂教学中,教师要为学生创设生与师,生与生,一对一,一对多等多向互动交流形式,使学生在活动中感受别人的思维方法和思维过程,同时,表达自己的思维过程,达到个性发展的目的。在刘老师的《植树问题》教学中,我们看到学生交流的形式有:语言陈述、画图展示、演算过程、表格列举、实物演示、现场模拟等,在多种形式的互动交流中凸显了策略性知识。 学生“用自己喜欢的方式”做数学,体现了多元化的交流方式。通过交流,或互补,取长补短,变式拓展;或说明,正反举例,左右印证;或争论,争锋相对,面红耳赤。教育的艺术在于激励、唤醒与鼓舞,在这样真实、深入的交流中,学生思维的火花在碰撞中被擦亮、 点燃, 学生的潜能得以开启、个性得到张扬。 学生参与其中,不仅知其然还知其所以然,策略性知识自然凸显。
例如,刘杰老师执教《植树问题》,学生在交流时出现了以下几种方法:
100÷5=20(棵)
100÷5=20(棵) 20+2=40(棵)
100÷5=20(棵) 20+1=21(棵)
100÷5=20(棵) 20+1=21(棵) 21×2=42(棵)
针对这些方法,老师没有急于评判,而是请这样做的同学上台讲解,说明自己的道理。有的是理直气壮,头头是道,边说边展示自己的过程,说得大伙心服口服;也有的边画边说,说着说着,就不能自圆其说而主动说“错了”;还有的被大伙质疑、反驳,使出十八般武艺,举例、演示、画图……学生在争辩中说服了或被说服了。过程是最美丽的风景,在学生开放的展示交流互动中,在学生脸蛋发红,眼睛发亮中,我们看到了思维的火花,“植树问题” 的策略性知识在学生的自主交流中自然地“凸显”了出来。
三、多角度归纳提炼,构建策略性知识
在学生的充分互动交流后, 教师引导学生静下来,回顾反思学习的过程,通过猜想、操作,有的发现:画了4 棵树得到3 个间隔;也有的画了10 棵树,得到9 个间隔,还有的画了21 棵树得到20 个间隔……在学生得到的丰富感性材料的基础上,教师用课件逐步呈现:

由此学生发现:“两端都栽的情况下,棵数比间隔数多1”的规律。 在这里,数学的数、形、式、文多种方式综合呈现,相得益彰,数学知识得以深刻理解。更可贵的是,刘老师没有停留在解决了这个问题,发现了这个规律上,而是将学生的思维进一步引向数学的本质上:“我们在解决这个问题的过程中,用了哪些方法策略? ”学生通过回忆、思考,交流,最后总结出:
1.可以把抽象的文字题的信息和问题用直观形象的线段图表示, 这就是数学上常用的数形结合的思想,画图的策略。
2.可以用一个“△”代表栽的一棵树,用“—”代表一个间隔,通过摆“△”和“—”,发现了两端都栽的情况下,棵数与间隔数间的关系。 这种用符号表示抽象的事物及其关系,简单明了,渗透了符号化意识,同时也将一一对应的策略性知识植入了学生的心中。
3.通过列表举例,从简单的数量开始,一一列举,发现规律,从而找到答案,进而发现“两端都栽的情况下,有n 个间隔,就要栽n+1 棵树”的规律。这种列举的策略,化繁为简的策略应运而生,逐步构建。
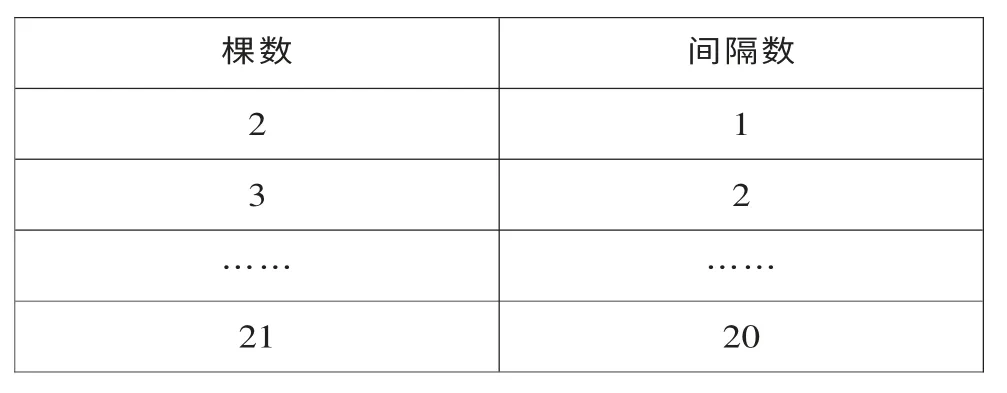
棵数 间隔数2 1 3 2…… ……21 20
通过引导学生交流、反思,知识在不断的内化中升华,更重要的是提炼了数学的思想方法,构建了问题解决的策略性知识,将数学的思想方法的“根”植入了学生的心中,关注了数学的本质,自然展现了数学学习的魅力。波利亚强调:要把“有益的思考方式、应有的思维习惯”放在数学教学的首要地位。要强化数学思想方法的教学,学生一旦掌握数学思想方法,对知识的理解就会更深刻,记忆就会更长久,思维就会更灵活,解决问题的能力就更强,并且学生在这个过程中也会进一步体验到数学活动的价值和乐趣。因此,我们要重视在教学中渗透数学思想方法策略,并引导学生回顾反思,提炼构建策略性知识。
四、多层次练习巩固,提升策略性知识
学生的数学能力不仅仅在于其掌握数学知识的多少,而是看他能否运用数学知识、数学思想、方法策略去解决实际问题。围绕学习内容,根据教学目标设计富有层次的,形式新颖的,具有典型性的练习题进行练习,引导学生在练习中巩固,在练习中比较,在练习中反思总结方法策略, 就能进一步提升问题解决的策略性知识,真正实现“授人以渔”。
如,刘杰老师在《植树问题》一课,在练习中注意了以下几点:
1.设计了与例题同类的基础题,进行巩固,达到“人人都能获得良好的数学教育”的目标。
2.设计了变式拓展练习:从“植树”拓展到“路灯”、“排队”、“敲钟”;从解决“栽多少棵树”拓展到解决“第一棵到最后一棵有多远”的问题;在题型上也克服了形式单一的弊端,有口答题、看图编题并解答、图文结合的情景题、应用问题等,鼓励学生挑战选作,学生在练习中自觉运用画图的策略、运用化繁为简的策略解决了问题。多层次、多角度的变式拓展练习,达到了“保底促优”,“不同的人在数学上得到不同的发展”的目标。
3.鼓励学生交流汇报自己的思考过程和运用策略,同时还引导学生反思比较题的异同,达到了举一反三的目的,提高了学生灵活解决问题的能力,并进一步提升了问题解决的策略性知识。同时,教师还引导学生在练习中对 “植树”、“路灯”、“排队”、“敲钟”问题进行比较,发现相同点,明确了“植树问题”的共同特征,进一步建构了“植树问题”的模型,促使学生真正“获得良好的数学教育”。
在小学数学教学中,“问题解决”的内容蕴含着学生终身受用的重要的策略性知识,教师在引导学生解决问题的过程中,一定要为学生搭建多元学习平台,助推“问题解决”策略性知识的形成。 实现“人人都能获得良好的数学教育,不同的人在数学上得到不同的发展”的目标。
