维修时间截尾序贯验后加权检验的实现*
2014-07-10刘勇徐廷学彭军
刘勇,徐廷学,彭军
(海军航空工程学院 a.接改装训练大队;b. 2系,山东 烟台264001)
0 引言
经典的维修性指标验证方法所需的样本量较大,但由于条件、经费等因素的限制,获取很多的现场数据和进行大量的维修性试验面临巨大困难。为此,基于Bayes理论的小子样检验方法在工程应用上获得了成功。这些方法主要有验后似然比检验[1]、序贯概率比检验[2-3]和序贯验后加权检验(sequential posterior odd test, SPOT)[4-9],其中SPOT方法是基于Bayes理论的小子样检验方法的核心。SPOT方法尽可能地利用未知参数的验前信息,在每次试验之后作统计判断,若尚不足以作出决定,就进行下一次试验,故试验次数并不是固定的。但出于试验时间和经费的考虑,并不能无限制地序贯下去,因此,有时会在试验前就把所需试验次数即试验样本量的上界确定下来,这时就称为截尾SPOT方法[6]。应用截尾SPOT方法时,如果截尾后仍不能用SPOT方法进行判决,则需要引入决策阈值并对之进行求解。部分学者文献对决策阈值的求解问题进行了研究,但未给出可行的实现方法。为了能将此方法应用于工程实践,本文在满足检验精度的情况下尝试用近似计算的方法代替积分运算,并通过某导弹维修性指标验证的实例证明了该方法的可行性。
1 截尾SPOT方法介绍
由于一般可认为系统维修时间服从正态分布或对数正态分布,所以本文按正态分布来讨论。当维修时间服从对数正态分布时,将维修时间以及可接受值作对数变换。
设系统维修时间均值的可接受值为μ1,检验假设为
H0:μ≤μ1,H1:μ>μ1.
若Y=lnX~Nθ,σ2,σ2已知,对μ1的转换方法为
θ1=lnμ1-σ2/2.
于是检验假设可更改为
H0:θ≤θ1,H1:θ>θ1.
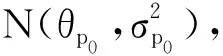
(1)
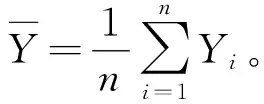
(2)
有了上述公式计算ON,然后引入A,B两值进行判决检验。
设2类假设的验前概率分别为PH0和PH1,取
(3)
PH1=1-PH0,
(4)
式中:Φ(·)为标准正态分布函数。
若生产方和使用方风险值分别为α和β,则
(5)
(6)
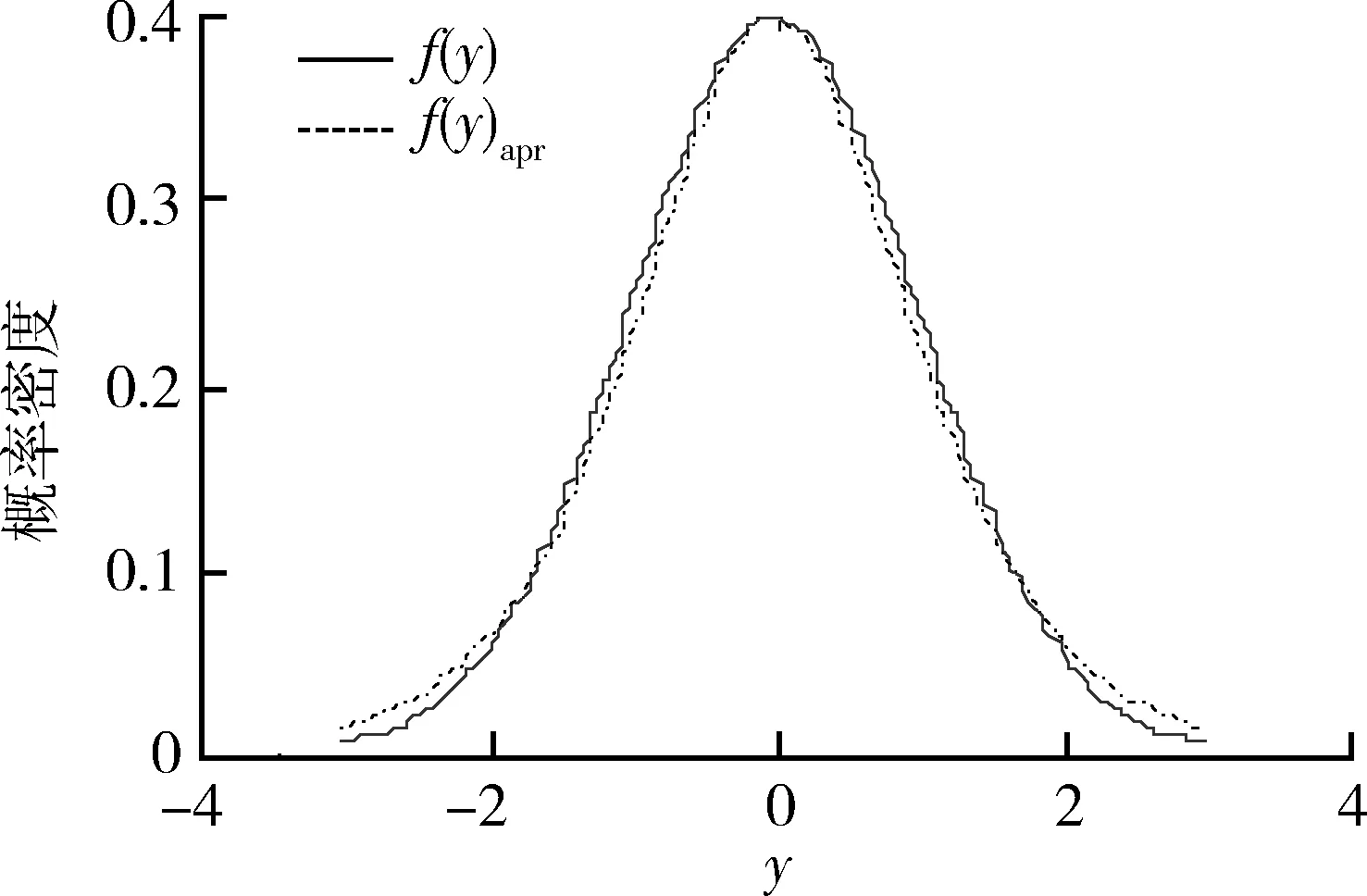
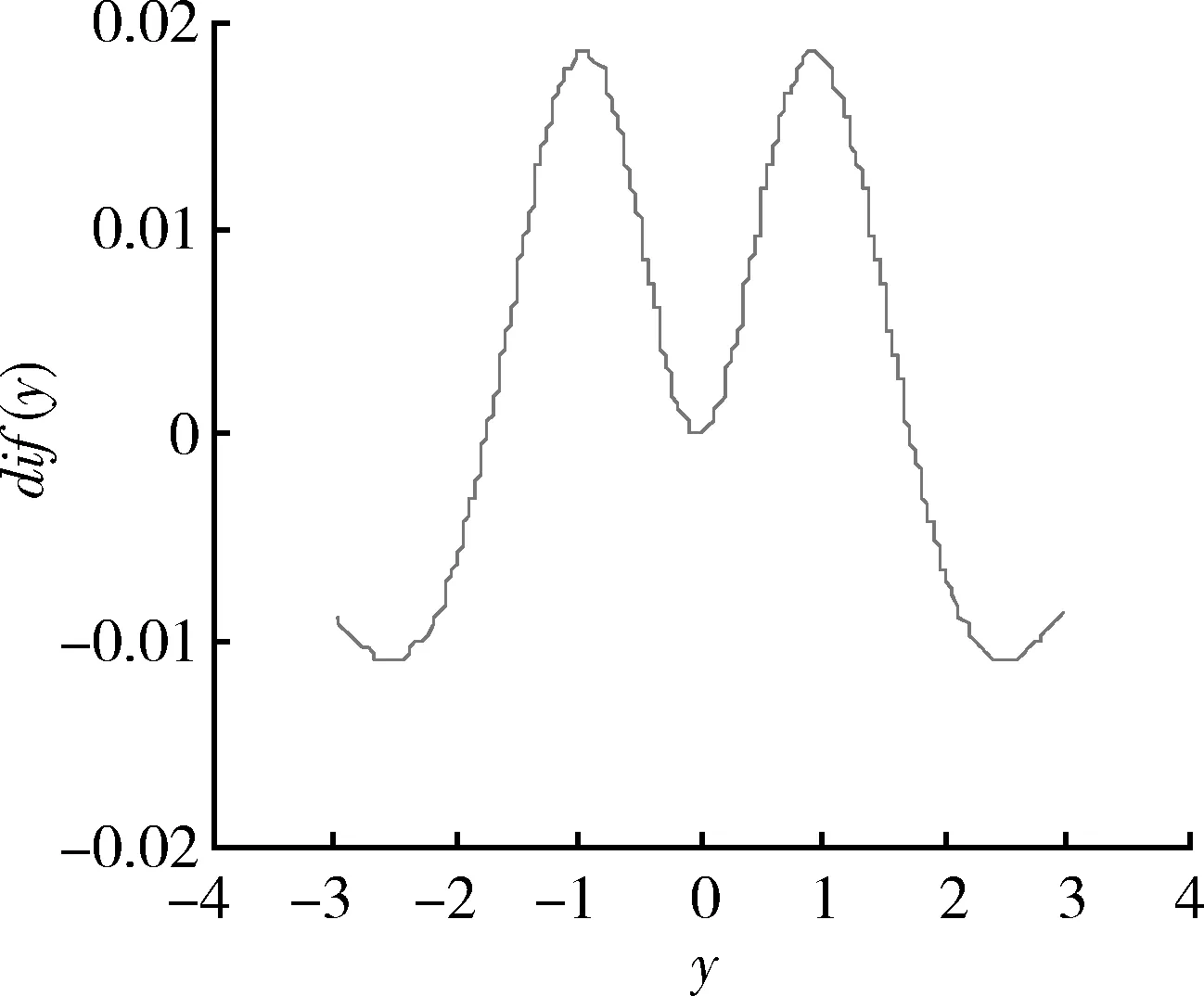
如果在试验之前就确定了样本量N,在N次试验后有A D1={Ω:A 判决检验如下: (1) 当A (2) 当C 由文献[4, 12]可知 (7) 且有 (8) 式中: 式中:Z1/(B+1)为标准正态分布的1/(B+1)分位点。 (2) 计算p(i)。 p(i)的精确表达式为 (9) (3) 若τ>ε,进行如下判断 令i=i+1,转(2)。 式(9)的Φ(·)中含有未知数θ。因为Φ(·)没有关于θ的解析表达式,因此不能直接对式(9)等号右边的部分进行积分运算。p(i)的计算是关键的一个环节,为此,接下来对此作进一步的探讨。 当不能进行积分运算时,可以寻找近似计算方法作为替代。 设Y~N0,1,其分布函数为 (10) 其概率密度函数为 (11) (12) 相应的密度函数为 (13) (14) 图1 f(y)与f(y)aprFig. 1 Curves of f(y) and f(y)apr 图2 近似与积分运算的相对误差曲线Fig.2 Curve of relative error between approximate calculation and integral calculation 由图2可看出,近似计算与积分运算的相对误差小于2%,满足工程上计算判别的需要,因此,这里用式(14)替代式(10),以实现p(i)的计算。这样就有 (15) 于是 (16) (17) 将式(16)和(17)代入式(9),最终可得到p(i)的计算模型为 (18) 在定型阶段对某导弹的平均修复时间MTTR进行检验,规定α=β=0.1,对MTTR的最大可接受值μ1=42 min,最大试验样本量N=8。已知维修时间X服从对数正态分布,维修时间的对数方差为σ2=0.162,即Y=lnX~N(θ,0.162);求得θ的先验分布为N(3.721,0.020)。 H0:θ≤3.730, H1:θ>3.730. 此时Θ=Θ0∪Θ1,其中Θ0={θ≤θ0},Θ1={θ>θ0}。 经过现场试验,得到了8个维修时间数据,对之取对数,如表1所示。 表1 现场维修时间数据及其对数Table 1 Field maintenance data and their natural logarithms 由式(3)和(4)可得 P(H0)=0.526, P(H1)=0.474. 于是根据A,B的计算公式(5)和(6),可以得到 A=0.048, B=17.122. 显然有A 在应用截尾SPOT方法进行维修性指标验证的过程中,现有基于数值逼近原理求解决策阈值的方法存在的难题是积分变量中含有的正态分布积分函数没有解析表达式,因此不能直接进行积分运算。为此,本文在满足检验精度的情况下,用近似计算的方法代替正态分布积分运算,给出了一种求解决策阈值的可行方法。用此方法对某导弹MTTR进行验证的实例表明用近似计算代替积分运算的方法是有效的,且可以看出,相比传统的统计试验方法,基于Bayes理论的截尾SPOT方法减少了试验次数,能够缩短试验时间,提高军事效益。 参考文献: [1] 刘颖, 杜健. 基于Bayes理论的装备维修性验证方法[J]. 装甲兵工程学院学报, 2011, 25(1): 18-21. LIU Ying, DU Jian. Maintainability Verification Method for the Equipment Based on Bayes Theory[J]. Journal of Academy of Armored Force Engineering, 2011, 25(1): 18-21. [2] 黄寒砚, 王磊. 基于参数优化的截尾序贯检验法[J]. 飞行器测控学报, 2011, 30(3): 49-55. HUANG Han-yan, WANG Lei. Truncated Sequential Test Based on Parameter Optimization[J]. Journal of Spacecraft TT&C Technology, 2011, 30(3): 49-55. [3] WILLIS A J. Design of a Modified Sequential Probability Ratio Test (SPRT) for Pipeline Leak Detection[J]. Computers and Chemical Engineering, 2011, 35(1): 127-131. [4] 董博超, 宋保维, 梁庆卫, 等. 武器装备小子样维修性试验与评定方法研究[J]. 兵工学报, 2011, 32(3): 327-330. DONG Bo-chao, SONG Bao-wei, LIANG Qing-wei, et al. Research on Small Sample Maintainability Experimentation and Evaluation of Weapon System[J]. Acta Armamentll,2011,32(3):327-330. [5] 王雪峥,韩成哲.可靠性试验中多参数空间复杂假设的SPOT方法研究[J].战术导弹技术.2010,(1):48-52. WANG Xue-zheng, HAN Cheng-zhe. Development of SPOT Method for Multiple Parameter Spaces with Complex Hypothesis in Reliability Test[J]. Tactical Missile Technology, 2010(1): 48-52. [6] 巨养锋,张曼菊,邵铭,等. 序贯验后加权检验法在激光告警试验中的应用[J]. 激光技术, 2009, 33(6): 667-669. JU Yang-feng, ZHANG Man-ju, SHAO Ming, et al. Sequential Posterior Odd Test Approach in Laser Warning System Test[J]. Laser Technology, 2009, 33(6): 667-669. [7] 黄秀平, 周经伦, 冯静. 装备部件平均修复时间的序贯验后加权检验方法[J]. 装备制造技术, 2008(6): 1-3. HUANG Xiu-ping, ZHOU Jing-lun, FENG Jing. The Sequential Posterior Odd Test for the Mean Time to Repair of the Armored Vehicle’s Components[J]. Equipment Manufacturing Technology, 2008(6): 1-3. [8] MAO Zhao-yong, SONG Bao-wei. The Sampling Inspection Method Based on Sequential Posterior Odd Test[C]∥ 2010 International Conference on Computational and Information Sciences,2010:163-166. [9] GUO Bo, JIANG Ping, XING Yun-yan. A Censored Sequential Posterior Odd Test (SPOT) Method for Verification of the Mean Time to Repair[J]. IEEE Transactions on Reliability, 2008, 57(2): 243-247. [10] 张守玉, 封伟书. 基于随机加权法的装备平均维修时间验证研究[J]. 装备指挥技术学院学报, 2009, 20(3): 100-103. ZHANG Shou-yu, FENG Wei-shu. Study of Equipment MTTR on Random Weighted Method[J]. Journal of the Academy of Equipment Command & Technology, 2009, 20(3): 100-103. [11] 贾占强, 蔡金燕, 梁玉英. 基于改进Bootstrap和Bayesian Bootstrap的小样本产品实时性能可靠性评估[J]. 计算机应用研究, 2009, 26(8): 2851-2854. JIA Zhan-qiang, CAI Jin-yan, LIANG Yu-ying. Real-Time Performance Reliability Evaluation Method of Small-Sample Based on Improved Bootstrap and Bayesian Bootstrap[J]. Application Research of Computers, 2009, 26(8): 2851-2854. [12] 黄秀平. 装甲装备维修性试验数据处理和小子样验证方法[D]. 长沙: 国防科学技术大学, 2008. HUANG Xiu-ping. Armored Equipment Test Data Processing and Small Sample Demonstration Method[D]. Changsha: National University of Defense Technology, 2008. [13] 刘清珺, 陈婷, 陈舜琮. 正态分布积分近似计算公式及其在实验结果判定中的应用[J]. 现代测量与实验室管理, 2009(3): 21-23. LIU Qing-jun, CHEN Ting, CHEN Shun-cong. Normal Distribution Integral Approximate Calculation Formula and Its Application in Experimental Result Determination[J]. Modern measurement and Laboratory Management, 2009(3): 21-23.


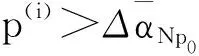
2 决策阈值的近似计算方法
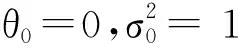
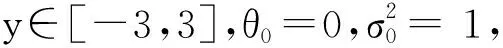

3 案例分析

4 结束语
