基于小生境遗传算法的干扰资源调度研究*
2014-07-10雷磊周青松张剑云刘春泉
雷磊,周青松,张剑云,刘春泉
(1.电子工程学院,安徽 合肥 230037; 2.北京电子设备技术研究所,北京 100191)
0 引言
在未来战场中,作战任务要求和环境日益复杂多样,对作战武器系统电子对抗能力的要求也越来越高,而对多雷达目标的干扰决策能力就是衡量电子对抗能力的一个重要指标。以我方攻击机对敌方空域进行突防的典型战场态势想定为例,我方综合运用多部干扰机实施远距离支援干扰和伴随干扰,但在干扰资源有限、任务时间紧迫等不利条件下,可能同时遭遇敌方多部不同类型雷达的探测,若不能及时制定有效的干扰决策、采取有效的干扰措施进行掩护,一旦被敌方地空、空空武器平台跟踪锁定,后果不堪设想。因此,如何对敌方多部探测雷达实施有效的干扰、实现“隐身”突防就成为一个极富意义和挑战的研究课题。
干扰机的资源调度是建立在雷达侦察的基础上,综合分析敌方布防雷达参数,实时解算探测雷达数量、探测距离、威胁等级,并结合我方干扰机的工作效能,制定干扰方案,形成干扰决策[1]。文献[2-4]分别将基于投影梯度、0-1规划和最大元素算法的资源分配方法运用到了类似的问题中,取得了一定的效果,但随着雷达数M和干扰资源数N的增加,该问题涉及的解空间呈指数级增加,容易出现计算量的组合爆炸现象[5],上述方法难以高效求解。文献[6]在问题的求解中引入了遗传算法,并运用基于Grefenstette等在解决TSP问题时提出的巡回路线编码方法,解决了常规编码方法所对应的交叉运算和变异运算会使子代群体中产生较多不满足问题约束条件的分配方案的问题,但由于编码方式的限制,实际上是对模型和解空间作了额外的约束,削弱了模型和算法的普遍适用性。文献[7]在无线自组网多目标优化资源选择模型中引入了一种基于整数编码的改进遗传算法,弥补了二进制编码和实数编码在处理此类问题时的缺陷,但仍然存在传统遗传算法处理此类问题时易出现的收敛稳定性差和容易早熟等问题。
文献[8]中首先提出了基于小生境思想的改进型遗传算法,其基本思想是:首先给出群体中各个染色体之间的距离定义,然后两两比较个体之间的距离。若小于预设值D,则选择二者中适应度值较低的个体,极大地降低其适应度。经此处理,距离较近的较差个体在后续竞争中将会逐渐被淘汰,因而数代之后在距离D之内将只存在一个的较优者。这样既维护了群体的多样性,又使得种群中的各个个体之间保持了一定的距离,从而使个体能够在整个约束空间中分散开来,保证了有效基因的传递性。
本文从干扰压制概率公式出发,建立了雷达干扰资源调度模型。然后采用基于整数编码的小生境遗传算法对模型进行寻优求解,有效改善了传统遗传算法收敛速度慢、计算结果稳定性差以及容易早熟等问题,相较其他文献方法,能够进一步提升算法的整体寻优能力。
1 雷达干扰资源调度的数学模型
雷达干扰资源调度优选问题从本质上可以归结为一个多目标规划问题,即在一系列节点、链路上优化一个反映某些参数指标的资源约束函数,并据此寻找满足目标约束条件的满意解。下面基于多目标规划方法,建立雷达干扰资源调度的数学模型。
由雷达原理可知,一般地,在虚警概率Pfa一定时,信噪比SNR越大,发现概率Pd越大,即雷达发现目标的概率是以信噪比为自变量的增函数[9]。这里可以按照文献[5]中计算发现概率Pd和压制概率Q的方法对二者进行计算。显然,发现概率Pd越小,压制概率Q越大,干扰机对雷达的干扰效果就越好,所以可用压制概率Q作为干扰压制效果的评估准则。
假设在某次突防任务中,我方可用干扰资源由N部干扰机组成,集合为J={J1,J2,…,JN},干扰方式为压制式干扰;需要干扰的敌方布防雷达网由M部雷达组成,集合为R={R1,R2,…,RM}。因为各部雷达的探测性能、工作方式、开机时间以及布防区域均有所差别,所以各部雷达的威胁等级也不尽相同,因此不妨设第j部雷达的威胁等级为Lj,j=1,2,…,M,并规定威胁等级越大,其对突防任务的威胁程度就越高,需要对其分配更多的干扰压制,以保证干扰掩护的整体效果。为方便计算,对Lj进行归一化处理,可得第j部雷达的威胁权系数为
(1)
由文献[5]计算方法可得如下的干扰效能矩阵
(2)
式中:Qij为第i部干扰机对第j部雷达的干扰压制概率,i=1,2,…,N,j=1,2,…,M。
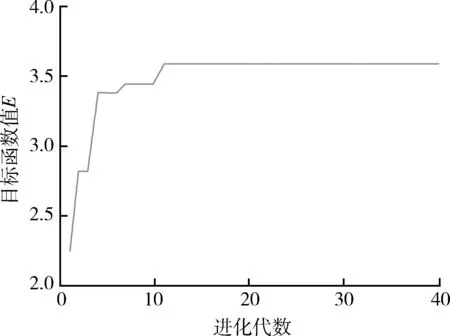
为简化模型,设定干扰策略原则为:采用干扰效益最大准则,优先分配威胁等级较大的雷达;每部干扰机在某一时刻只能集中功率干扰一部雷达;某部雷达在某一时刻可不被干扰机干扰,也可被多部干扰机同时干扰。在这里应注意2点:一是部分文献[5-6]在设定干扰策略原则时规定“每部雷达在某一时刻中至少分配一部干扰机”,这实际上是忽略了可能存在的“某部雷达威胁等级较低时,综合考虑整体的干扰效益,可选择不对其分配干扰资源,而是将多余的资源分配给威胁等级较高的雷达,进行重点干扰”的实际情况,这样虽然模型求解时的速度较快,但却是在以降低模型和算法的普遍适用性为代价减小解空间,因此本文并未直接采用这些文献中的模型,而是对模型的约束条件作了相应的改进;二是若N 根据上述原则,可得N部干扰机对M部雷达实施干扰的资源调度模型目标函数为 (3) 其约束条件为 式中:E为干扰资源调度的整体效益;xij=1时表示将第i部干扰机分配给第j部雷达,xij=0时则表示不分配。 由分析可知,式(3)的干扰资源调度问题为一种多参数、多约束的非线性整数规划问题,属于NP难问题。当干扰机数N和雷达数M增大时,干扰资源调度问题的解空间呈指数级增加[11],常规方法难以高效地求解此类优化问题,因此,可采用小生境遗传算法进行优化求解。 为进一步避免算法中存在的收敛速度慢、计算结果稳定性差以及容易早熟等问题,应对基本小生境遗传算法进行一定的改进。其具体实现步骤如下: 步骤1 编码 编码的目的就是把自变量在解空间中的数据表示成遗传空间中的基因型结构数据,其基本的码型有0-1编码、整数编码和实数编码等。二进制编码计算量大,权系数的表示精度受到限制;而对于变量离散型的问题,采用实数编码的GA(genetic algorithm)得到的最优解必须离散化归整处理,结果往往不再是全局最优,对于多约束的优化问题甚至会产生不可行解[7]。为此,文献[12]提出了基于整数编码的改进遗传算法,兼具二进制编码和实数编码的优点,具有很好的全局收敛性能。因此,本文采用整数编码,编码得到的基因串用一个整数数列表示,顺序值表示干扰机的编号,整数值表示雷达的编号,如一个染色体为[5,1,4,2,3,4],其表示将第1部干扰机分配给第5部雷达,第2部干扰机分配给第1部雷达,第3部干扰机分配给第4部雷达,……,第6部干扰机分配给第4部雷达。这样就可以将干扰资源调度方案转化为一个整数编码的基因串,并且这种对应是唯一的。 步骤2 初始群体的产生 采用随机方法产生K个维数为N的整数向量,每个向量作为一个独立的染色体;向量的维数N代表染色体上基因的个数,即干扰机的个数;每个基因取≥1,≤M的整数,M为雷达的数量;K个染色体作为一个种群,每个染色体表示为Xi,t,i表示染色体在种群中的序列,1≤i≤K,t表示遗传代数,G表示最大的遗传代数,1≤t≤G。 步骤3 构造适应度函数 遗传算法在搜索进化过程中一般不需要其他外部信息,仅用评估函数值来评估个体或解的优劣,并作为以后遗传操作的依据。这里根据第1部分中的目标函数式(3)来评估群体中的每个个体的适应度。 步骤4 选择 本文将选择分为2步,首先从得到的子代个体中预选出前K个较优个体(这里初始群体的个数为K),让它们成为下步遗传操作中的备选父代。然后利用轮盘赌的方法选出实际参与交叉操作的父代个体。为了避免传统轮盘赌方法易出现的“一枝独秀”而使得优化问题陷于局部解的现象,对其进行如下改进:将群体中的染色体按照适应度由好到坏进行排序,即序号越小,对应的个体越优,那么其被选中的概率也就越大。其后的个体被选中的概率应逐步减小,但也不宜过小。这里可生成一个向量 P=P0,P1,P2,…,Pi,…,PK, 然后在0,PK内产生均匀分布的随机数r,若Pi-1≤r≤Pi,就选择第i个染色体放入交叉队列,i=1,2,…,K。重复上述步骤,直至得到含有K个实际参与交叉操作父代个体的交叉队列。 步骤5 交叉 为了克服收敛对于初始群体选择的依赖,可采用4种不同的交叉操作,并在后代生成的过程中两两交替使用这4种操作。 在奇次代中使用单点交叉和多点交叉操作生成子代染色体: (1) 单点交叉操作 随机选择一个初始基因位,便得到了从首位基因到初始基因位的一个基因段,然后再随机选取2个染色体,将二者的上述相应基因段进行交换,得到2个新的子代个体。 (2) 多点交叉操作 与单点交叉操作类似,不同的是被交换的基因段是由随机产生的2个初始基因位决定的。 在偶数代中使用差分进化和内插/外推操作生成子代染色体: (1) 差分进化操作 (4) 式中:i=1,2,…;F∈0,2,用于控制差分项的幅度,在仿真中可根据具体情况进行设定。 得到新染色体后需对超出边界和非整数的基因进行强制规整赋值:若xi,j≤1,则令xi,j=1;若xi,j≥M,则令xi,j=M;若1 (2) 内插/外推操作 (5) 式中:i=0,1,2,…;C∈0,0.5,用于控制内插/外推的幅度,在仿真中可根据具体情况进行设定。然后再对每个基因采用类似于差分进化中规整赋值的方法进行处理。 步骤6 变异 每一代的交叉操作完成后,应随机选取少数子代个体进行变异操作,其具体操作类似于初始群体中个体的产生。通常情况下,应使变异个体数占总群体数目的1%~2%。此外,由于在遗传操作的后几代,染色体会相继进入局部解,所以可以在一定代数之后稍微增大变异概率,以使其突破局部限制,收敛到全局最优解。 步骤7 评价适应度函数 与步骤3类似。 步骤8 小生境淘汰运算 步骤9 精英保留策略 如果经过步骤8得到的种群的最优值劣于父代,则需用父代种群中的最优个体代替子代中的最差个体,以使后代种群的最优值不差于前代,提高算法的收敛效率。 小生境遗传算法的具体实现流程如图1所示。 图1 小生境遗传算法流程图Fig.1 Flow chart of niche genetic algorithm 为了验证本文算法的有效性,这里给出基于整数编码小生境遗传算法的雷达干扰资源调度的计算机仿真结果。设作战区域中5部干扰机对5部雷达进行干扰,5部雷达的威胁系数分别为0.80,0.76,0.84,0.86,0.90,根据干扰机和雷达各自参数性能、空间位置关系和压制时间段的设置,利用压制概率计算方法,可得干扰决策矩阵,如表1所示。 表1 干扰效能数据列表Table 1 Performance data of interference 设定参数,令整数编码小生境遗传算法的初始种群中个体数目K=20,最大进化代数G=40,差分幅度控制系数F=1,内插外推系数C=0.25,参量ε=0.5,β=0.92,α=0.098 6,变异概率取0.015,小生境个体间最小欧几里德距离预设值D=1。 优化结果为:gbest=[1,5,3,2,4],其所对应的适应度函数值为3.579 4,其结果与用匈牙利算法进行的优化结果一样,说明了本文算法的正确性。其干扰资源调度方案表示为:第1部干扰机干扰第1部雷达,第2部干扰机干扰第5部雷达,依此类推。 图2给出了目标函数的收敛特性。 图2 目标函数的收敛曲线Fig.2 Convergence curve of objective function 从图2中可知,本文算法目标函数的上升,分了几个不同的阶段,这是因为雷达干扰资源调度的目标函数是非线性的多峰函数,这些不同的阶段正好说明了整数编码小生境遗传算法的正确性和有效性,能够很好地减小搜索过程陷入到局部最优解的概率,从而提高算法的寻优能力。 为了验证本文算法的优越性,这里再给出本文算法与其他文献算法的计算机仿真结果比较。在上述参数均相同的情况下,将文献[6]算法与本文算法进行对比,二者各独立运行500次,算法性能对比结果如表2。 表2 两种算法的性能对比结果Table 2 Comparisons of performance obtained with two different methods 从表2可以看出,虽然2种算法多次运行后都可以最佳收敛到全局最优解,但本文算法的收敛稳定性明显高于文献[6]算法,且本文算法的最差收敛结果和目标函数收敛后的平均值也明显优于文献[6]算法。同时,以上性能的提升所付出的代价是耗时的小幅增加。 在上述参数不变的情况下,再将二者各独立运行100次,收敛误差对比结果如图3所示。 a)文献[6]算法的收敛误差图 b)本文算法的收敛误差图图3 收敛误差对比结果Fig.3 Comparisons of convergence error 从图3中可知,运行100次后,本文算法的非最优收敛次数和最差收敛误差分别为6次和0.202 6,均优于文献[6]算法的27次和0.358 6,因此,本文算法较文献[6]算法有明显优势。 本文提出了一种基于整数编码小生境遗传算法的雷达干扰资源调度方法,采用实数编码,以最大化雷达干扰资源调度的整体效益为目标函数,在遗传进化过程中交替使用4种交叉方式。最后,通过仿真实验说明了该方法的正确性和优越性,相较文献方法,本文方法在有效提升最优收敛稳定性的前提下,可进一步提升最差收敛的目标函数值和目标函数收敛后的平均值,同时有效地控制了收敛误差,因此能够使雷达干扰资源调度的整体效益达到最优。 参考文献: [1] 裴立彬,刘春生. 宽带阵列的同时多目标干扰资源调度研究[J]. 电子对抗信息技术,2012,25(6):46-54. PEI Li-bin, LIU Chun-sheng. Jamming Strategy of Wide-Band Array to Multi-Target[J]. Electronic Information Warfare Technology, 2012, 25(6): 46-54. [2] 徐振海,王雪松,肖顺平,等. 雷达组网对抗中遮盖干扰功率优化分配[J]. 系统工程与电子技术,2003,25(6):655-657. XU Zhen-hai, WANG Xue-song, XIAO Shun-ping, et al. Optimum Allocation of Barrage Jamming Power in Netted Radar Countermeasure[J]. Systerns Engineering and Electronics, 2003, 25(6): 655-657. [3] 沈阳,陈永光,李修和. 基于0-1规划的雷达干扰资源优化分配研究[J]. 兵工学报,2007,28(5):528-532. SHEN Yang, CHEN Yong-guang, LI Xiu-he. Research on Optimal Distribution of Radar Jamming Resource Based on Zero-One Programming[J]. Acta Armamentarii, 2007, 28(5): 528-532. [4] 李波,高晓光. 编队空战中协同电子干扰的功率分配[J]. 系统工程与电子技术,2008,30(7):1298-1300. LI Bo,GAO Xiao-guang. Algorithm of Power Allocation for Cooperative Electronic Jamming in Air Combat of Formation [J]. Systems Engineering and Electronics, 2008, 30(7): 1298-1300. [5] 刘以安,倪天权,张秀辉,等. 模拟退火算法在雷达干扰资源优化分配中的应用[J]. 系统工程与电子技术,2009,31(8):1914-1917. LIU Yi-an, NI Tian-quan, ZHANG Xiu-hui, et al. Application of Simulated Annealing Algorithm in Optimizing Allocation of Radar Jamming Resources [J]. Systems Engineering and Electronics, 2009, 31(8): 1914-1917. [6] 高彬,吕善伟,郭庆丰,等. 遗传算法在电子战干扰规划中的应用[J]. 北京航空航天大学学报,2006,32(8):933-936. GAO Bin, LÜ Shan-wei, GUO Qing-feng, et al. Genetic Algorithm Approach to the Jammer’s Layout for EW[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(8): 933-936. [7] 刘勇,张晓红. 遗传算法的多目标优化资源选择算法[J].火力与指挥控制,2009,33(2):89-92. LIU Yong, ZHANG Xiao-hong. Research on Resource Selection Algorithm of Multi-Objective Optimization Based on Genetic Algorithms[J]. Fire Control and Command Control, 2009, 33(2): 89-92. [8] DEB K, GOLDBERG D E. An Investigation of Niche and Species Formation in Genetic Function Optimization[C]∥Proceedings of the Third International Conference on Genetic Algorithms, 1989:42-50. [9] 丁鹭飞,耿富录. 雷达原理[M]. 西安:西安电子科技大学出版社,2002. DING Lu-fei, GENG Fu-lu. Radar Principle[M]. Xi’an: Xidian University Press, 2002. [10] 胡运权. 运筹学教程[M]. 北京:清华大学出版社,1998. HU Yun-quan. The Tutorial on Operational Research[M]. Beijing: Tsinghua University Press, 1998. [11] PARSOPOULOS K E, VRAHATIS M N. Recent Approaches to Global Optimization Problems Through Particle Swam Optimization[J]. Natural Computing, 2002, 1(2-3): 235-306. [12] 廖美英,郭荷清,张勇军. 一种整数编码的改进遗传算法[J]. 计算机工程与应用,2003(1):103-105. LIAO Mei-ying, GUO He-qing, ZHANG Yong-jun. An Ameliorative Integer Coded Genetic Algorithm[J]. Computer Engineering and Applications, 2003(1):103-105.
2 基于整数编码小生境遗传算法的干扰资源调度优化
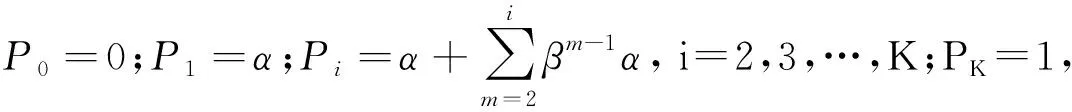


3 仿真实验
3.1 算法正确性验证

3.2 算法优越性验证



4 结束语
