基于直觉模糊聚类算法的导弹打击目标规划*

贺小亮，满莉

(1.第二炮兵工程大学 初级指挥学院，陕西 西安 710025； 2.国防大学 研究生学院，北京 100091)

0 引言

导弹主要用于打击敌纵深战略战役目标，其以射程远、精度高、毁伤大等优点成为我军联合火力打击行动中的一支重要力量。合理的目标规划是导弹火力运用的核心问题之一，对整个作战进程影响重大。由于目标的多属性特点，在规划时各属性存在一定的模糊特征。传统的模糊聚类算法对目标规划分类时，对单一的隶属度函数依赖较重，不能充分利用各模糊属性信息，有一定的局限性。

直觉模糊集[1-5]是对Zadeh模糊集的一种重要扩充和拓展，其隶属度函数μA(x)、非隶属度函数γA(x)及直觉指数πA(x)可以分别表述x对集A支持、反对及中立的程度，因而有效克服了Zadeh模糊集单一隶属度函数的局限性，能够更加细腻地描述客观对象的模糊性本质[6]。

基于此，本文利用直觉模糊集的这类优点，将直觉模糊聚类算法用于导弹打击目标规划领域。首先设计了隶属度函数和非隶属度函数，将目标特征和规划标准进行直觉模糊化，然后根据直觉模糊特征量的相似度函数和相异度函数构建相似矩阵，并计算其等价矩阵，最后利用直觉模糊等价矩阵进行聚类分析，实现了目标的规划。

1 目标处理

鉴于导弹打击目标的特点，本文主要针对战略性目标开展研究。战略目标的相对重要性是受多属性影响的，因此这是一个多属性目标规划问题。经查阅资料[7]，选择以下8种影响因素：人口、面积、工业产值、政治重要性、军事重要性、文化重要性、战略地位及威胁程度。目标的规划标准可划分为：重要、较重要、一般、不重要，4类标准等级，将每一个待评价的战略目标视为待规划的具体对象，要决定它相对于4个标准等级的相对归属即决定其相对重要性。

设待规划目标包括n个对象A=A1,A2,…,An，每个对象包括8个属性Ai=(xi1,xi2,…,xi8)，i=1,2，…,n。按照目标规划的需求，设定目标规划标准，同样，规划标准也具有8个属性，设为B=B1,B2,B3,B4，Bi=(xi1,xi2,…,xi8)，i=1,2,3,4。

2 直觉模糊聚类算法

2.1 数学描述

定义1 直觉模糊集[1]：设X是一个给定论域，则X上的一个直觉模糊集A为

A=(x,μA(x),γA(x))|x∈X，

(1)

式中：μA(x):X→0,1和γA(x):X→0,1分别代表A的隶属函数μA(x)和非隶属函数γA(x)，且对于A上的所有x∈X,0≤μA(x)+γA(x)≤1成立。对于X中的每个直觉模糊子集，称πA(x)=1-μA(x)-γA(x)为A中x的直觉指数，它是x对A的犹豫程度的一种测度。显然，对于每一个x∈X,0≤πA(x)≤1。

定义2 将目标原始信息直觉模糊特征化的隶属函数和非隶属函数分别为

(2)

(3)

式中：Amin和Amax分别为A(x)在论域X上的最小值和最大值；a≥1，用来调节犹豫度，当a=1，犹豫度为0，当a→∞，犹豫度→1-μA(x)，a一般取1～1.3[8]。

定义3 直觉模糊关系[9]。设X和Y是普通、有限、非空集合或论域。定义在直积空间X×Y上的直觉模糊子集成为从X到Y之间的二元直觉模糊关系。记为

R={[(x,y),μR(x,y),γR(x,y)]|x∈X,y∈Y}，

(4)

式中：μR(x):X×Y→0,1和γR(x):X×Y→0,1满足条件0≤μR(x,y)+γR(x,y)≤1，∀(x,y)∈X×Y；

用IFR(X×Y)来表示X×Y上的直觉模糊子集的全体。若X和Y为有限集时，即X=x1,x2,…,xm，Y=y1,y2,…,yn，则从X到Y之间的二元直觉模糊关系R可以用矩阵表示，记为R=(μij,γij)m×n。

定义4 直觉模糊相似矩阵[10]。若直觉模糊关系矩阵R=(μij,γij)m×n满足下列条件：

(1) 自反性。(μii,γii)=(1,0),i=1,2,…,n；

(2) 对称性。(μij,γij)=(μji,γji),i,j=1,2,…,n，

则称R为直觉模糊相似矩阵。

本文利用直觉模糊相似度[11]和相异度[12]，构造直觉模糊相似矩阵。设论域包括n个待规划对象A={A1,A2,…,An}，每个对象包括m个属性Ai=(xi1,xi2,…,xim)，对象的属性数据均使用直觉模糊集表示，记其隶属度为μAi(xk)，非隶属度为γAi(xk)，直觉指数为πAi(xk)=1-μAi(xk)-γAi(xk)，其中i=1,2,…,n；k=1,2,…,m。Ai与Aj之间的相似度为

(5)

Ai与Aj之间的相异度为

(6)

设μij=S(Ai,Aj)，γij=D(Ai,Aj)，则R=(μij,γij)n×n为满足定义3的关于n个对象A=A1,A2,…,An的直觉模糊相似矩阵[13]。

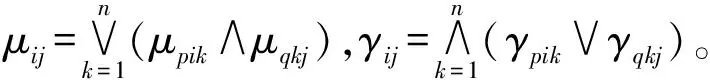
直觉模糊关系矩阵的合成运算，完全是直觉模糊关系合成的一种矩阵表达形式，合成矩阵的每个元素也是“∧-∨”运算的结果，目的是得到等价矩阵。

定义6 直觉模糊等价矩阵。若直觉模糊矩阵R=(μij,γij)n×n满足下列条件：

(1) 自反性同定义3；

(2) 对称性同定义3；

(3) 传递性。R2=R∘R⊆R，即

则称R为直觉模糊等价矩阵。

定义7 直觉模糊集的截集[13]：设A={(x,μA(x),γA(x))|x∈X}为有限论域X上的一个直觉模糊集，对0≤α,β≤1，且α+β≤1，称集合A(α,β)={x|μA(x)≥α,γA(x)≥β,x∈X}为直觉模糊集A的(α,β)截集，(α,β)称为置信水平或置信度。

设R=(μij,γij)n×n为直觉模糊等价矩阵，定义其(α,β)截矩阵为R(α,β)=(r(α,β)ij)n×n，其中

(7)

显然，截矩阵R(α,β)是布尔矩阵，用模糊聚类的方法，可由截矩阵R(α,β)按照目标规划标准实现对象A=A1,A2,…,An的规划分类。

2.2 计算步骤

(1) 将目标的指标值和目标规划标准建立增广的目标指标值矩阵

所谓增广的目标指标值矩阵，是将n个待规划目标对象A和目标规划标准B的指标值构造成矩阵。据此得到增广的目标指标值矩阵X。

(8)

式中：i=1,2，…,n+4；j=1,2，…,8。

(2) 建立标准化矩阵[7]

将步骤1得到的增广的目标指标值矩阵X，按照式(9)，计算得出标准化矩阵Y。

(9)

Y=(yij)(n+4)×8，i=1,2，…,n+4；j=1,2，…,8.

(3) 建立直觉模糊特征矩阵

根据定义2，将步骤2得到的标准化矩阵Y，按照式(2)，(3)分别求出目标信息的直觉模糊特征，隶属度μAi(xj)和非隶属度γAi(xj)，进而得出直觉模糊特征矩阵Y′。

Y′=(μAi(xj),γAi(xj))(n+4)×8，i=1,2，…,n+4;

j=1,2，…,8

(4) 建立直觉模糊相似矩阵

根据定义4，直觉模糊特征矩阵Y′按照式(5)，(6)，计算得到直觉模糊矩阵的相似度和相异度，构造直觉模糊相似矩阵R。

R=(μij,γij)(n+4)×(n+4)，i=1,2，…,n+4；

j=1,2，…,n+4.

(5) 建立直觉模糊等价矩阵

根据定义5和定理1，通过合成运算，由相似矩阵R求取直觉模糊等价矩阵Rn。

(6) 建立截矩阵R(α,β)，进行聚类分析[15]

根据定义7，对等价矩阵Rn，合理设定置信度(α,β)，得出截矩阵R(α,β)，之后进行聚类分析。根据每列对应元素是否为1，找出每列对应的目标和规划标准等级，进而得出聚类结果。

3 仿真应用

根据目标处理结果，每个战略目标包括8个指标：人口、面积、工农业产值、政治重要性、军事重要性、文化重要性、战略地位及威胁程度。在上述指标中，人口单位：万人；面积单位：km2；工农业产值单位：万；其余指标均为[0,1]上无量纲数。设定待规划战略目标个数为6，A=A1,A2,…,A6，目标规划标准B=B7,B8,B9,B10，分别对应：重要、较重要、一般、不重要。参照文献[7]的数据建立战略目标指标值和规划标准指标值，如表1。

按照直觉模糊聚类算法，将表1中的6个目标,依照4个标准等级，进行规划分类。

(1) 构造增广的目标指标值矩阵

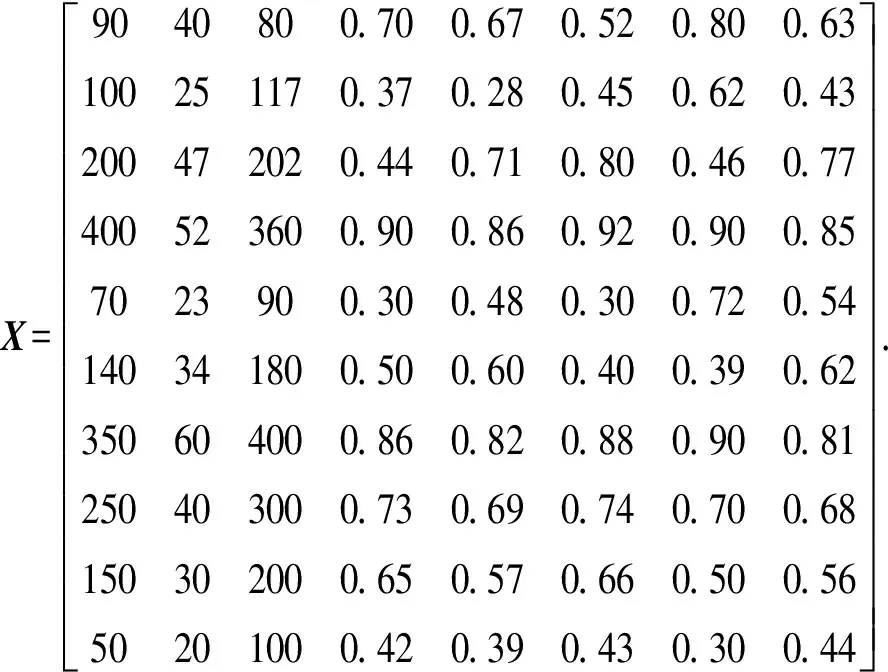
(2) 计算标准化指标值矩阵

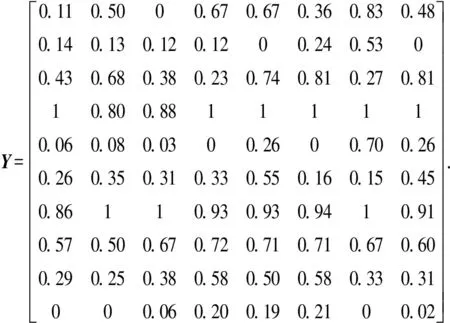
(3) 计算直觉模糊特征矩阵

按照步骤3和定义2，取a=1.2，计算直觉模糊特征矩阵，

(4) 计算相似矩阵

按照步骤4，为了简化计算取p=1，计算相似矩阵，

(5) 计算相似矩阵R的等价矩阵

采用平方的方法，进行合成运算，发现R2≠R；再次进行合成运算，R4≠R2；进一步计算后，R16=R8，那么R8为直觉模糊等价矩阵，即

(6) 计算截矩阵和聚类分析

在设定置信度时，等价矩阵根据选取的置信度数值，按式(7)计算得出截矩阵，此时，设定的置信度水平，应保证截矩阵每列为1的目标元素对应该列中为1的规划标准元素仅有1个，即规划分类的目标仅对应1个规划标准。因此，取置信度(α,β)=(0.77,0.21)，按照步骤6，计算等价矩阵R8的截矩阵为

针对截矩阵R(0.77,0.21)的结果，进行聚类分析。根据每列的元素是否为1进行区分，得出聚类结果，A1,A3,B8，A2,A5,B10，A4,B7，A6,B9。可见，6个战略目标的规划结果为：目标A4为重要目标，目标A1和A3为较重要目标，目标A6为一般目标，目标A2和A5为不重要目标。本算例所有计算是由Matlab编程实现。

4 结束语

本文通过对导弹打击目标信息的原始数据标准化和直觉模糊化，运用直觉模糊聚类算法，实现了对导弹打击目标的规划分类。针对现有模糊聚类算法的局限性，利用直觉模糊集能够更好地描述事物的模糊性本质的优势，并运用隶属函数和非隶属函数，实现对目标信息原始数据的直觉模糊特征化；利用直觉模糊相似度和相异度构造了直觉模糊相似矩阵，进而计算得出等价矩阵；选取合适的置信度获得截矩阵，从而实现目标的规划分类，该方法概念清晰，计算简单。通过实例的仿真应用，表明该方法能够按照规划需求，较快的对目标进行规划分类，计算结果相对文献[7]更加准确，验证了算法的有效性和准确性。

参考文献：

[1] ATANASSOV K. Intuitionistic Fuzzy Sets [J]. Fuzzy Sets and Systems, 1986, 20(1):87-96.

[2] ATANASSOV K. More on Intuitionistic Fuzzy Sets [J]. Fuzzy Sets and Systems, 1989, 33(1):37-46.

[3] ATANASSOV K. New Operations Defined Over the Intuitionistic Fuzzy Sets [J]. Fuzzy Sets and Systems,1994,61(2):137-142.

[4] Supriya Kumar De, Ranjit Biswas, Akhil Ranjan Roy. Some Operations on Intuitionistic Fuzzy Sets [J]. Fuzzy Sets and Systems,2000,114(3):477-484.

[5] Atanassov Krassimir T, Kacprzyk Janusz, Szmidt Eulalia, et al. On Separability of Intuitionistic Fuzzy Sets [J]. Lecture Notes in Artificial Intelligence,2003,2715(1):285-292.

[6] 雷英杰，王宝树，胡军红. 直觉模糊等价矩阵构造方法[J]. 系统工程理论与实践，2007(7):127-131.

LEI Ying-jie, WANG Bao-shu, HU Jun-hong. Method for Constructing Intuitionistic Fuzzy Equivalent Matrixes [J]. Systems Engineering Theory & Practice,2007(7):127-131.

[7] 汪民乐，高晓光. 导弹攻击目标选择的Fuzzy方法[J]. 西北工业大学学报，2008,18(3)：387-391.

WANG Min-le,GAO Xiao-guang.A Fuzzy Method for Missile Terget Selection[J].Journal of Northwestem Polytechnical University,2000,18(3):387-391.

[8] 徐小来，雷英杰，戴文义. 基于改进微粒群算法的直觉模糊整数规划[J]. 计算机应用，2008,28(9)：2395-2396.

XU Xiao-lai, Lei Ying-jie, DAI Wen-yi. Intuitionistic Fuzzy Integer Programming Based on Improved Particle Swarm Optimization [J]. Computer Application, 2008,28(9):2395-2396.

[9] 蔡茹，雷英杰，申骁勇，等. 基于直觉模糊等价相异矩阵的聚类方法[J]. 计算机应用，2009,29(1):123-126.

CAI Ru, LEI Yjing-jie, SHEN Xiao-yong, et al. Clustering Method Based on Intuitionistic Fuzzy Equivalent Dissimilarity Matrix [J]. Computer Application,2009,29(1):123-126.

[10] 张洪美，徐泽水，陈琦. 直觉模糊集的聚类方法研究[J]. 控制与决策，2007,22(8)：882-888.

ZHANG Hong-mei, XU Ze-shui, CHEN Qi. On Clustering Approach to Intuitionistic Fuzzy Sets [J]. Control and Decision,2007,22(8):882-888.

[11] LIU H W. New Similarity Measures Between Intuitionistic Fuzzy Sets and Between Elements [J]. Mathematical and Computer Modelling, 2005,42(1-2):61-70.

[12] LI D F. Some Measures of Dissimilarity in Intuitionistic Fuzzy Structures [J]. Journal of Computer and System Sciences, 2004,68(1):115-122.

[13] 贺正洪，雷英杰，王刚. 基于直觉模糊聚类的目标识别[J]. 系统工程与电子技术，2011，33(6)：1283-1286.

HE Zheng-hong, LEI Ying-jie, WANG Gang. Target Recognition Based on Intuitionistic Fuzzy Clustering [J]. Systems Engineering and Electronics, 2011，33(6)：1283-1286.

[14] ZHAO F X, MA Z M, YAN L. Fuzzy Clustering Based on Vague Relations [C] ∥ Proc. of the Fuzzy Systems and Knowledge Discovery，Xi′an, 2006: 79-88.

[15] XU Z H, CHEN J, WU J J. Clustering Algorithm for Intuitionistic Fuzzy Sets [J]. Information Sciences, 2008,178(19):3775-3790.