改进IMM的两飞行体无源定位跟踪算法*

高宪军,霍长庚,谈欣荣

(空军航空大学 科研部,吉林 长春 130022)

0 引言

两飞行体间的相对定位难点主要表现在2个方面：一是飞行器间的相对测量信息较少，依靠单一时刻的量测信息无法实现两飞行期间的相对定位；二是两飞行器间复杂的相对运动形式，使得精确的跟踪方程难以建立，从而影响跟踪算法的精度。针对上述困难，本文选择了基于相位差变化率[1-2]的无源定位方法对两飞行体进行相对定位。单纯利用无源定位技术不足以获取运动目标连续的位置信息，对于运动目标而言需要进行有效的跟踪滤波。

在机动目标跟踪领域，交互式多模型(interacting multiple model,IMM)算法[3-6]被认为是迄今为止最有效的算法之一。交互式多模型算法考虑了模型的特点，它假设目标有多种运动状态，每一种运动状态对应一种模型，目标在任意时刻的运动状态都可以用给定模型中的一种来表示，而运动状态的变化也就是运动模型之间的切换用齐次马尔可夫链表示，目标的滤波结果是多个模型滤波结果的加权综合。对于不同的应用要求，IMM算法又可能结合多种滤波算法。在这些算法中，各个模型匹配的都是卡尔曼滤波器(Kalman filter,KF)或者无迹卡尔曼滤波器(unscented Kalman filter,UKF)。这样做有算法简单，计算量小等优点，但是这些算法存在线性化误差，估计精度不高，且不适用于非高斯问题。

对于大多数的无源定位系统而言，其所提供的测量数据与目标状态间常呈非线性关系。如果希望利用观测数据完成目标状态的更新，必须解决非线性滤波问题。近几年，粒子滤波(particle filtering,PF)被应用于目标跟踪，成功地解决了滤波的非线性非高斯问题。将IMM算法与粒子滤波相结合的IMMPF(interacting multiple model particle filter)[7-10]算法采用交互式多模型结构来描述目标的运动过程，采用粒子滤波算法进行目标状态估计，集成了IMM对机动目标跟踪的良好特性，同时避免了线性化误差和高斯噪声的限制，有效地提高了状态估计的精确度。然而，粒子滤波的主要问题是巨大的计算量，若多模型中每个模型匹配一个粒子滤波器，计算量无疑会很大，影响跟踪的实时性。

针对以上问题，本文提出了一种改进的IMM滤波算法(IMMK-UKF-PF)进行定位跟踪。其原理是：将系统的多模型分成3类，①线性模型，匹配无迹卡尔曼滤波；②三阶及三阶以下非线性高斯模型，匹配无迹卡尔曼滤波；③三阶以上非线性高斯模型或非高斯模型，匹配粒子滤波。仿真结果表明该算法大大改善了计算效率。

1 利用相位差变化率的两飞行体二维相对定位原理

为了便于实现二飞行器间的相对定位，本文首先建立两飞行器A和B的相对坐标系如图1所示。

图1 两飞行器相对定位中的相对坐标系Fig.1 Relative coordinate system between two aircrafts in the relative location

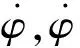
在二维平面上，观测站载机在机身上设置双阵元E1,E2，由于信号到达干涉仪天线的时间有先后，导致干涉仪接收到的信号存在相位差φt，则在某时刻t，

(1)

式中:d为基线间间距;λ为信号波长;w0为辐射波角频率;Δt为辐射波到达两阵元的时间差;βt为辐射源的方位角。

经过一系列的推导可得

(2)

由三角函数定义可推出

(3)

(4)

(5)

(6)

式中：x，y为t时刻的相对位置。

当目标辐射源运动时，由于无法得到目标的运动速度，此时不能对目标进行即时定位，因而必须在此基础上通过相应的滤波算法对目标速度进行估计和逼近，从而得到目标的速度和位置。

2 IMMK-UKF-PF滤波算法

设一个使用确定模型集合M=Mii=1,2,…,M的混合系统，状态方程和观测方程离散形式为

xik=Fixik-1+Givik-1，

(7)

zik=Hxik+rk，

(8)

式中：xik为在模型i(i=1,2,…,M) 下的目标运动状态矢量；vi为相应的非高斯过程噪声；zik为观测矢量；r为高斯观测噪声。

Qik和R分别为vik和rk的协方差。一共有M个模型，假设其中1到M1是线性的，M1到M2时是三阶及三阶以下非线性高斯模型，其他是三阶以上非线性高斯模型或非高斯模型。

系统模型之间的转移概率用一个马尔可夫链来表示：

Pmk+1=jmk=i=Pij，i,j=1,2,…,M.

(9)

图2给出了IMMK-UKF-PF滤波算法结构示意图。

从k-1时刻开始到k时刻，一个采样周期的IMMK-UKF-PF实现步骤如下：

(1)步骤1：输入交互

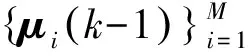
j=1,2,…,M，

(10)

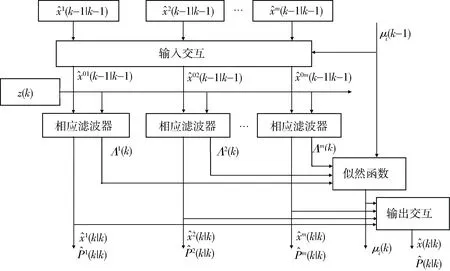
图2 IMMK-UKF-PF滤波算法结构示意图Fig.2 Filter algorithm structure of IMMK-UKF-PF

j=1,2,…,M.

(11)

三阶以上非线性高斯模型或非高斯模型中的粒子与其他模型估计值进行交互运算：

l=1,2,…,N;j=M2+1,M2+2,…,M,

(12)

(2) 步骤2：滤波

(3) 步骤3：模型概率更新

每一时刻模型概率都需要得到更新，模型1到M2有似然函数：

Λik=Nδik;0,Sik，i=1,2,…,M2.

(13)

其中残差的协方差计算如下：

(14)

而模型M2到M有似然函数：

i=M2+1,M2+2,…,M.

(15)

其中残差的协方差计算如下：

i=M2+1,M2+2,…,M.

(16)

各模型概率更新如下：

(17)

(4) 步骤4：输出交互

(18)

3 仿真验证

为了验证本文改进的IMM算法的有效性，将其与IMM-PF算法进行Matlab仿真，并将仿真结果进行比较分析。

仿真的软硬件环境为：联想IdeaPad Y450笔记本电脑，英特尔 酷睿2 双核 P7450 @ 2.13 GHz笔记本处理器器，2 G内存，Windows 7家庭普通板32位系统，Matlab 7.1软件仿真平台。

仿真中采用CV模型、CA模型和JERK模型[12]进行交互。

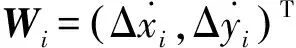
建立如下状态方程：

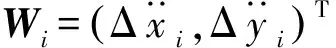
可以得到观测方程

式中：n1i，n2i，n3i，n4i为相互独立服从零均值高斯分布的测量误差。

当目标处于变加速运动时，x或y一维情况下状态转移矩阵为

p1=2-2αT+α2T2-2e-αT/2α3,

q1=e-αT-1+αT/α2,

r1=1-e-αT/α,

s1=e-αT,

式中:α为“机动”频率。

各模型滤波状态初始化，按照假定目标距离搜索范围为0～500 km，目标速度范围假定为-500～500 m/s，且初始分布假定为均匀分布，在此假定下由概率论知识得到目标位置和速度的期望值以及相应协方差值。X(0)=(4 000,3 000,250,450)T是初始状态矢量，P=diag(1,1,1,1)是初始状态协方差，各模型初始概率均为1/3，模型转移概率矩阵为

粒子滤波时模型的粒子数为N=800，采样周期为T=1 s，蒙特卡罗仿真次数为100。

仿真结果如图3～5所示，分别表示IMMPF,IMMK-UKF-PF2种算法估计目标位置的误差曲线。

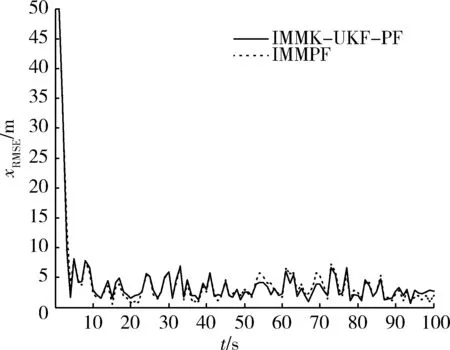
图3 x方向均方根误差Fig.3 Error of x direction

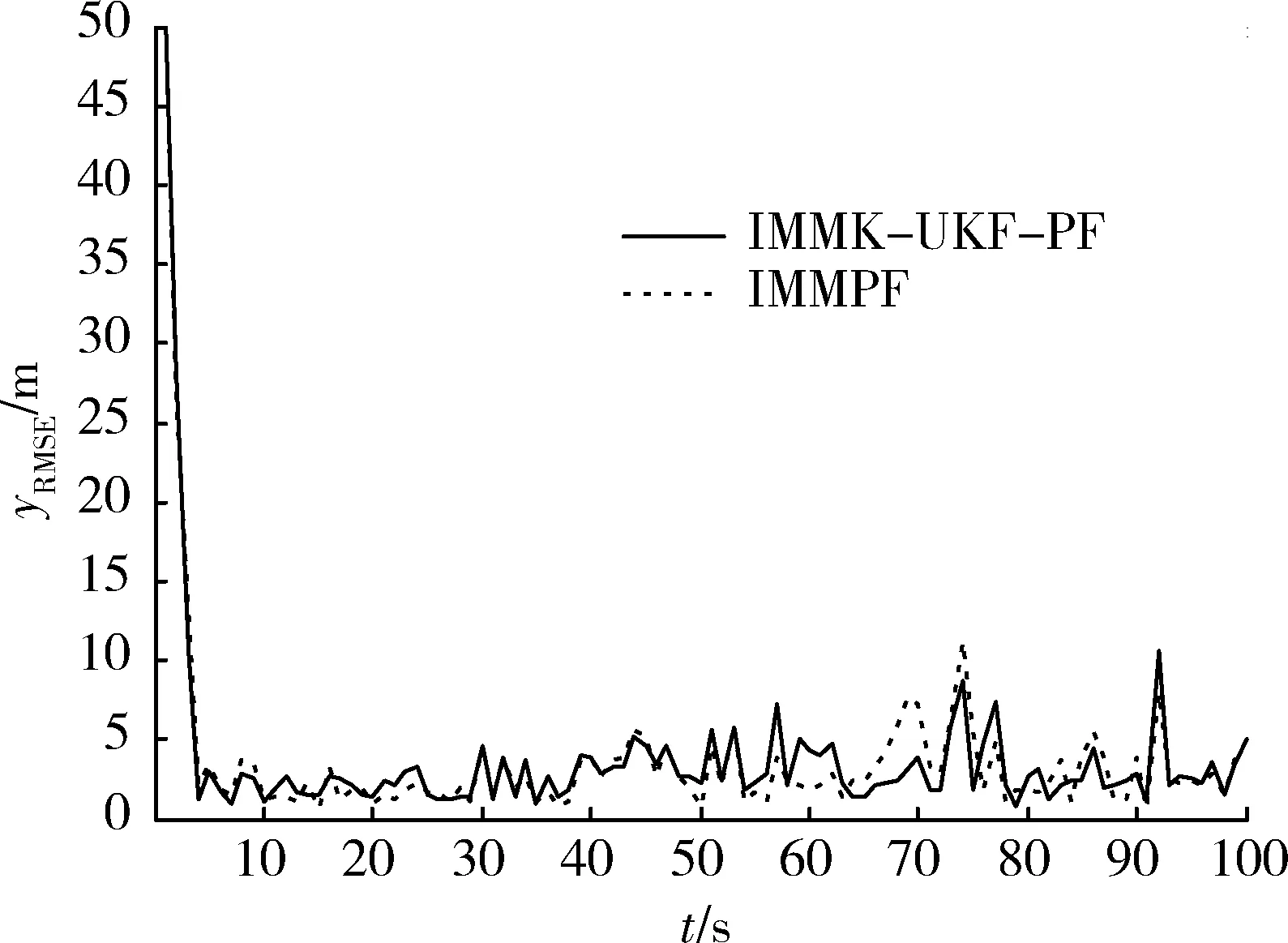
图4 y方向均方根误差Fig.4 Error of y direction

图5 r方向均方根误差Fig.5 Error of r direction

Execution time (seconds)

tIMMPF= 13.451 2，tIMMK-UKF-PF= 6.032 4.

由图3～5以及仿真时间可以得出，IMMK-UKF-PF滤波算法的均方根误差略小于IMMPF算法，跟踪性能有一定的改善，最重要的是仿真所用时间减少很多，这在现实应用中具有重要的意义。

4 结束语

本文在基于相位差变化率的两飞行体相对定位问题的基础上提出了一种改进的交互式多模型滤波算法(IMMK-UKF-PF)，利用不同的模型匹配不同类型的滤波器，IMMK-UKF-PF算法充分发挥了粒子滤波和无迹卡尔曼滤波以及卡尔曼滤波各自的优点，大大提高了计算效率，减少了跟踪定位所用时间，同时该算法具有良好的跟踪性能和较强的鲁棒性。在实际的机动目标跟踪中，目标的运动情况比较复杂，往往需要多个不同参数的线性及非线性模型进行匹配，在这种情况下，采用IMM-UKF-PF算法改善的计算负荷是可观的。

参考文献：

[1] 孙仲康，郭福成，冯道旺．单站无源定位跟踪技术[M]．北京：国防工业出版社，2008．

SUN Zhong-kang,GUO Fu-cheng,FENG Dao-wang.Passive Lacation and Tracking Technology by Single Observer [M].Beijing:National Defense Industry Press ,2008.

[2] 胡来招．无源定位[M]．北京：国防工业出版社，2004．

HU Lai-zhao.Passive Lacation [M].Beijing:National Defense Industry Press,2004.

[3] 梁彦,潘泉,杨峰,等.复杂系统的现代估计理论及应用[M].北京:科学出版社,2009.

LIANG Yan,PAN Quan,YANG Feng,et al.Modern Estimate Theory and Application in Complex System[M].Beijing:Seience Press 2009.

[4] MAZOR E,AVERBUCH A, BAR-SHALOM Y,et al. Interacting Multiple Model Methods in Target Tracking:A Survey[J]. IEEE Trans.on Aerospace and Electronic Systems,1998,34(1):103-122.

[5] BLOM H A P,BAR-SHALOM Y. The Interacting Multiple Model Algorithm for Systems with Markovian Switching Coefficients[J]. IEEE Trans on Automatic Control.1988,33(8):780-783.

[6] LI X R.Multiple-Model Estimation with Variable Structure-PartⅡ：Model-Set Adaptation[J]. IEEE Trans on Automatic Control,2000,45(11):2047-2060.

[7] BOERS Y,DRIESSEN J N. Interacting Multiple Model Particle Filter[J]. IEE Proc.-Radar Sonar Navig,2003,150(5):344-349.

[8] BLOM H A P,BLOEM E A. Particle Filtering for Stochastic Hybrid Systems[C]∥43IEEE Conference on Decision and Control.USA:IEEE,2004,3:3221-3226.

[9] MORELANDE M R,CHALLA S. Maneuvering Target Tracking in Clutter Using Particle Filters[J].IEEE Trans.on Aerospace and Electronic Systems,2005,41(1):252-270.

[10] MUKESH A Z, MERCHANT S N, UDAY B D. Arbitrary Trajectories Tracking Using Multiple Model Based Particle Filtering in Infrared Image Sequence[C]∥Proceeding of the International Conference on Information Technology:Code and Computer(ITCC04).Washington,USA:IEEE,2004.

[11] 宫淑丽,王帮峰,吴红兰,等.基于IMM算法的机场场面运动目标跟踪[J].系统工程与电子技术,2011,33(10):2322-2326.

GONG Shu-li,WANG Bang-feng,WU Xiao-lan,et al.Tracking of Moving Tragets on Airport Surface Based on IMM Algorithm[J].System Engineering and Electronics,2011,33(10):2322-2326.

[12] 李大治,程，皇甫堪.基于JERK模型的单站无源定位跟踪算法研究[J].系统仿真学报,2008,20(24):6750-6752.

LI Da-zhi,HUNAG Pu-kan.Research on Single Observer Passive Location and Tracking Algorithm Based on JERK Model[J].Journal of system simulation,2008,20(24):6750-6752.