Caputo 分数阶微分算子合成性质的推广①

秦彤晖， 张 笛

(中国矿业大学(北京)理学院，北京100083)

0 引言

分数阶微积分算子理论的研究近年来取得了蓬勃的发展[1～2]，受到了相关学者越来越多的关注[3～5]，分数阶积分算子和分数阶微分算子间的合成性质是进一步研究分数阶微分方程解的关键所在，特别地，在一般条件下对Caputo分数阶微分算子合成性质研究的文献较为罕见，本文应用分析的方法，给出了Caputo分数阶微分算子合成性质的一般形式．

1 预备知识

设函数f(x)在有限区间[a，b]上有定义且在[a，b]的任意子区间上可积，α ∈ C，其中Gamma函数Γ(z)=特别地，Gamma函数经延拓后有，则

定义 1[1]函数 f(x)的 α 阶 Riemann －Liouville分数阶左积分

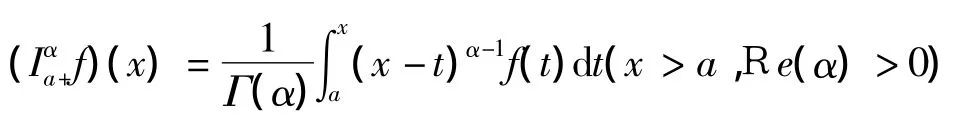
定义 2[1]函数 f(x)的 α 阶 Riemann －Liouville分数阶右积分

定义 3[1]函数 f(x)的 α 阶 Riemann －Liouville分数阶左微分

定义 4[1]函数 f(x)的 α 阶 Riemann －Liouville分数阶右微分

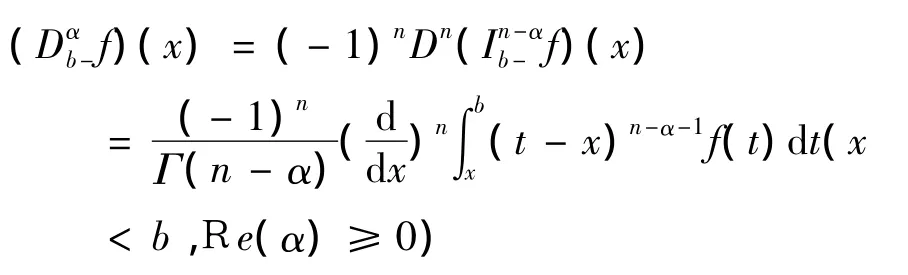
引理1．1[1]若 α，β ∈ C，Re(α)，Re(β)＞0，且 f(x)∈ Lp(a，b)(1 ≤ p≤ ∞)，则

引理1．2[1]若α，β∈C，Re(α)≥0，Re(β)＞ 0，则

引理1．3[1]若α∈C，R e(α)＞ 0，f(x)∈L1(a，)，则

引理1．4[2]若 α，β ∈ C，Re(β)≥ Re(α)＞ 0，m = [Re(β)] +1，f(x) ∈ L1(a，b)，∈ACm[a，b]，则

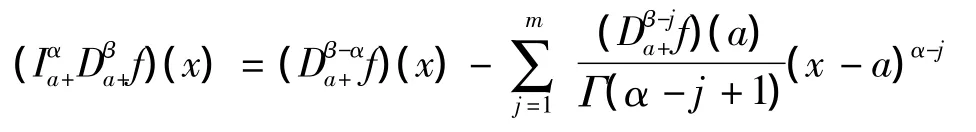
2 Caputo分数阶微分算子

定义2．1[1]函数f(x)的α阶Caputo分数阶左微分

定义2．2[1]函数f(x)的α阶Caputo分数阶右微分

引理 2．1[1]设 Re(α)≥0，n ∈ N，则

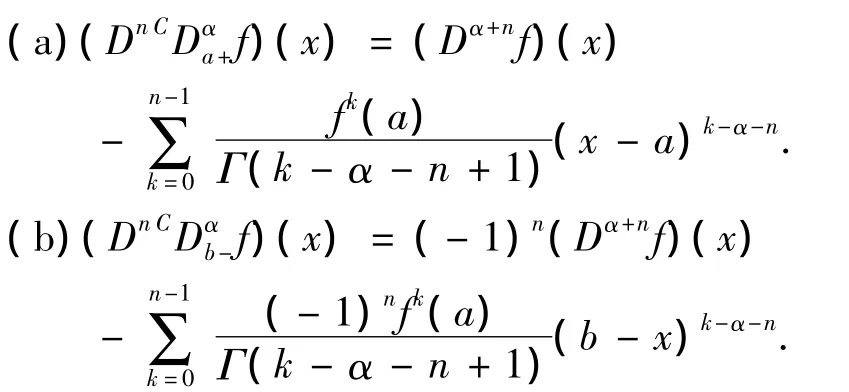
证明 由定义 2．1[1]，2．2[1]及引理 1．2[1]，2．1[1]可得证，故在此省略．

3 Caputo分数阶微分算子合成性质的推广

文献[1]中给出了Riemann－Liouville分数阶积分算子和Caputo分数阶微分算子阶数相同时的积分和微分间合成关系:

定理3．1[1]若α∈C，Re(α)＞ 0，当α∉N，f(x)∈Cn－1[a，b]或α∈N，f(x)∈Cn[a，b]时，则

现考虑把定理3．1[1]推广到一般情形．

定理3．2 若 α，β ∈C，Re(α)，Re(β)＞ 0，当α，β ∉N，m= [Re(β)]+1，f(x)∈Cm－1[a，b]或 α，β ∈ N，f(x)∈ Cm[a，b]时，则

证明(1) 当α，β∉N，f(x)∈Cm－1[a，b]时，由定义 2．1[1]得

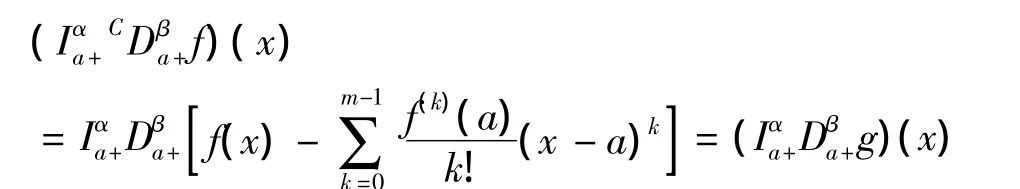
(a)当 Re(α)＞ Re(β)时，由引理1．1[1]及引理 1．3[1]得

对上式两边关于x求导得

所以，由引理 1．2[1]得

(b)当Re(β)≥Re(α)时，由引理1．4[2]得

令

由(a)知 h(x)=gm－β(x)

则(Dβ－ja+g)(a)=0

故由引理 1．2[1]得(2)当α，β∈N，f(x)∈Cm[a，b]时，由注2．1得

综上知，命题得证．

[1] A．A．Kilbas，H．M．Srivastava，J．J．Trujillo．Theory and Applications of Fractional Differential Equations[M]．vol．204 of North － Holland Mathematics Studies，Elsevier Science B．V．，Amsterdam，The Netherlands，2006．

[2] 郭柏灵，浦学科，黄凤辉．分数阶偏微分方程及其数值解[M]．北京:科学出版社，2011．

[3] 王小东．Riemann－Liouville分数阶微分及其性质证明[D]．太原:太原理工大学，2008．

[4] 武则女．分数阶导数、积分的性质及几何意义[J]．哈尔滨师范大学自然科学学报，2013，29(1):19 －22．

[5] 秦君琴．分数阶微积分的性质[J]．江苏师范大学学报(自然科学版)，2012，30(2):13 －14．