一类具分布时滞的退化微分系统周期解存在性①

王莉萍， 周宗福

(安徽大学数学科学学院，安徽合肥230601)

0 引言

微分系统的周期解一直是人们非常关注的问题，对于通常的微分系统，其周期解问题已被广泛地研究，而对于退化微分系统(也称广义微分系统)，目前周期解方面的结果不多．文献[1]利用不动点定理分析了一类退化中立型微分系统的周期解存在性．文献[2]研究了一类指标为1(参见[3])的具分布时滞的退化微分系统的周期解问题．关于指标为2情形的周期解问题研究，目前尚不多见，本文将对这一问题进行研究．

本文研究如下形式的具分布时滞的退化微分系统的周期解的存在性，其中x∈Rn，r＞0为常数，E，A∈ Rn×n，f∈ C1(R ×[－ r，0]× Rn，Rn)且 f(t+T，s，x)=f(t，s，t)，T ＞ 0 为常数，r(E)＜ n 矩阵对[E，A]正则且指标为2．

1 系统的转化及预备知识

在系统(1)中，由于[E，A]正则且指标为2，由文献[4]存在可逆矩阵 P，Q ∈ Rn×n，使得

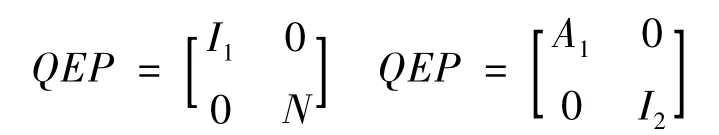
其中 I1，I2分别为 n1，n2阶单位阵，A1∈ Rn1×n1，N ∈Rn2×n2，且 N ≠ 0，N2=0，n1+n2=n．

对系统(1)作变换x(t)=Py(t)(且方程两边左乘Q)，则系统(1)即被化为

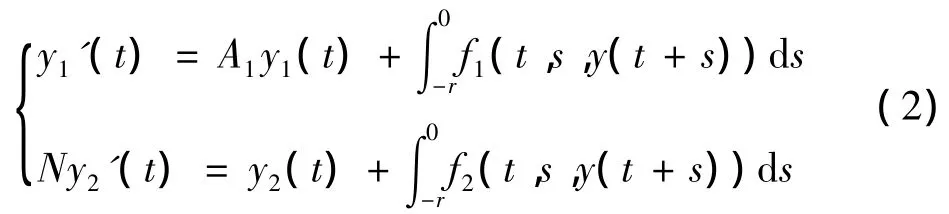
其中，

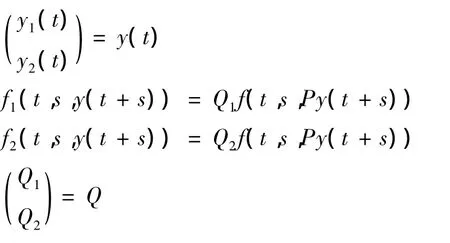
易知 f1(t，s，y)，f2(t，s，y)关 t是 T 周期的，且 f1∈C2(R ×[－ r，0]× Rn，Rn)，f2∈ C2(R ×[－ r，0]×Rn，Rn2)．

于是，讨论系统(1)的T周期解存在问题就转化为讨论系统(2)的T周期解存在问题．

引理1[2]设 y∈ C(R，Rn)(并不要求 y可微)，则∫0－rf2(t，s，y(t+s))ds可微，且

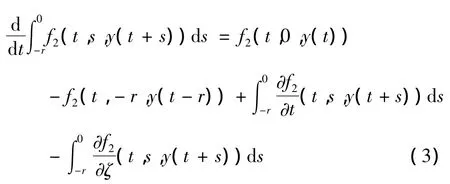
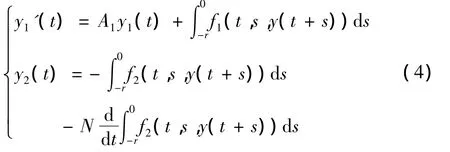
证明 证明比较显然，略去．

下面主要讨论系统(4)的T周期解存在性．

定义1[5]对矩阵A∈Rn×n，定义矩阵测度

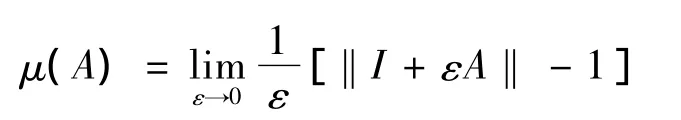
考虑线性系统

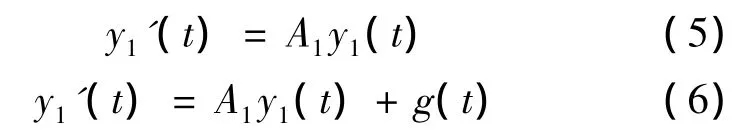
其中 A1∈ Rn1×n1，g:R → Rn1连续，且 g(t+T)=g(t)，T ＞ 0．

引理3[5]设Y(t)为(5)的基解矩阵，则

引理4[5]如果 μ(A1)＜0，则系统(6)存在唯一的T周期解

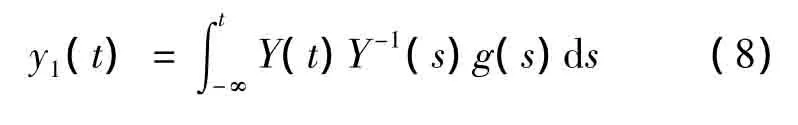
引理5[6](Krasnoselskii不动点定理)

设K为Banach空间X中的一个有界闭凸集，映射F:K→K及G:K→K满足:

(i)∀u，v∈ K，Fu+Gv∈ K;

(ii)F为全连续的，G为压缩的，则F+G在K上至少有一个不动点．

2 主要结果

记 E=C(R，Rn)，设

CT={u∈ E:u(t+T)=u(t)，t∈ R}

定理1 对于系统，假设

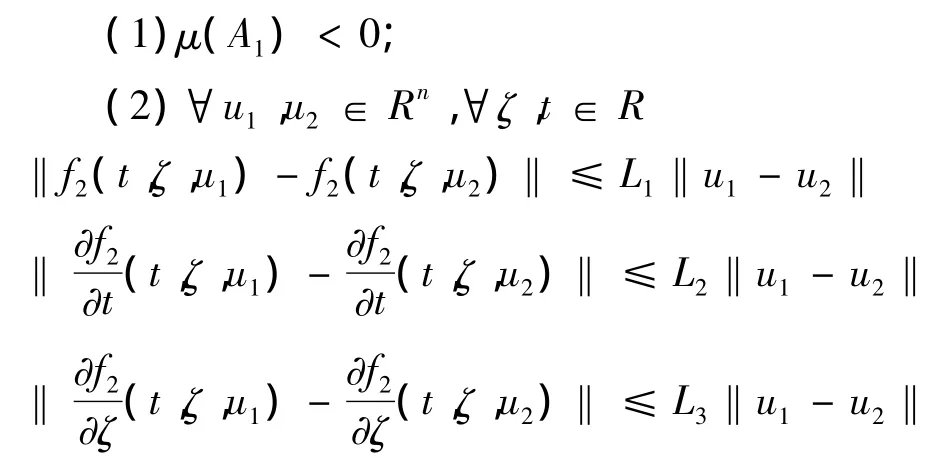
且

2(‖N‖ +r)L1+r‖N‖(L2+L3)＜1

其中 k=eμ(A1)T

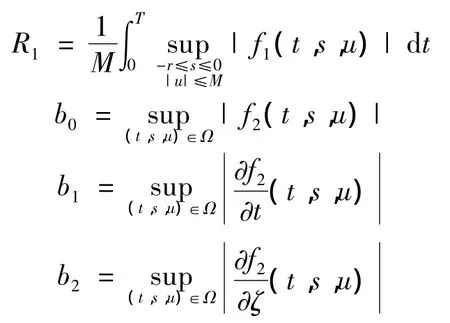
Ω ={(t，s，u)∈Rn+2，0≤t≤T，－r≤s≤0，|u|≤M}则系统(4)存在连续的T周期解．

任取u∈CT，考虑周期系统

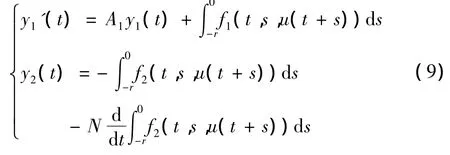
其中

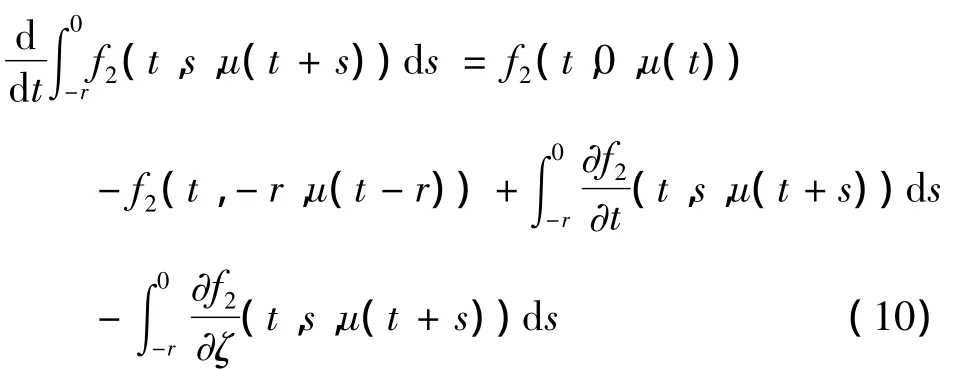
由引理4，系统(9)有唯一的T周期解

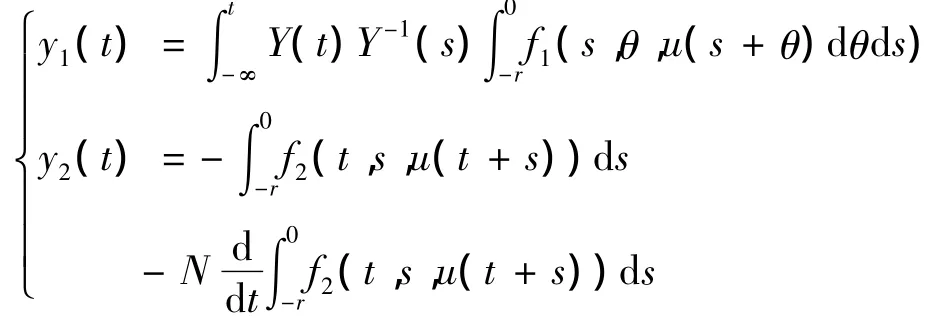
定义从CT到CT的算子F及G如下:

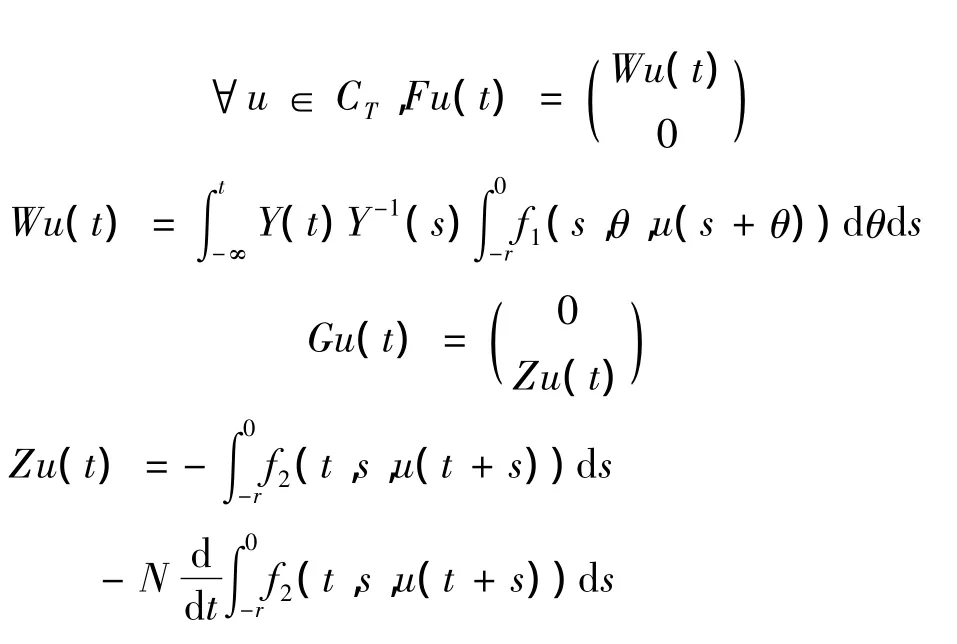
则算子F+G的不动点就是系统(4)的连续的T周期解．

令 K={u:u∈CT，‖u‖≤M}，则K为CT中的有界闭凸集．下面证明(1)∀u，v∈ K，Fu∈ K，Gv∈K，Fu+Gv∈K，(2)F在K上全连续，(3)G在K上为压缩的．

(1)∀u，v∈K由引理3及文献[6]中的定理1的证明方法可知

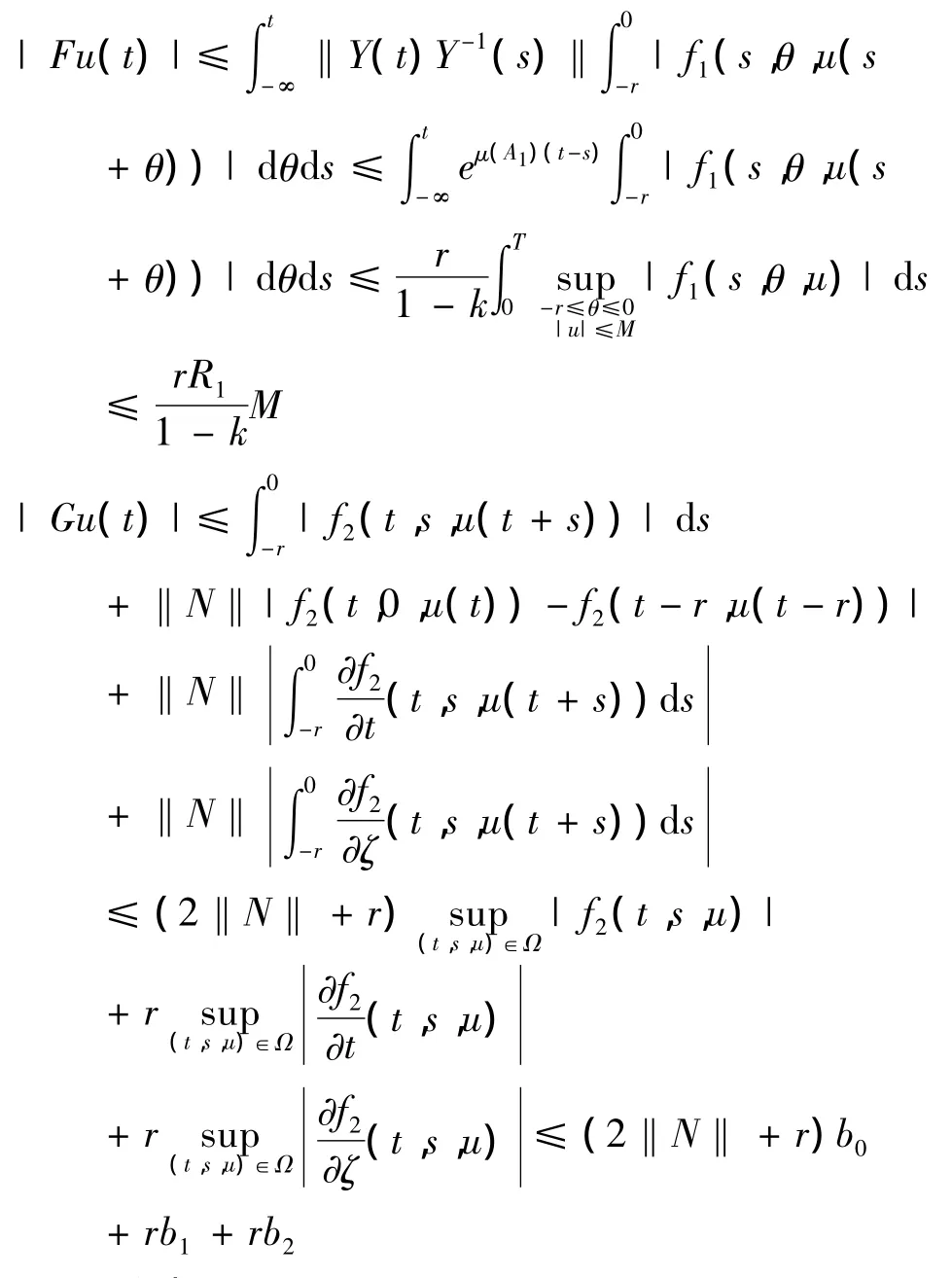
所以

从而‖Fu+Gv‖≤M，因此Fu+Gv∈K，由上述证明过程可以看出Fu∈K，Gv∈K．

(2)证明F在K上全连续．即证①F在K上是连续的;②F在K上是紧的．

①∀un，u ∈ K，若

类似(1)的证明过程可得

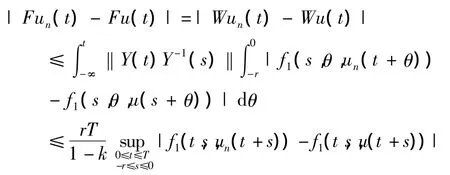
即有

由于f1(t，s，u)在Ω上一致连续，可知，当时，所以F在K上是连续的．

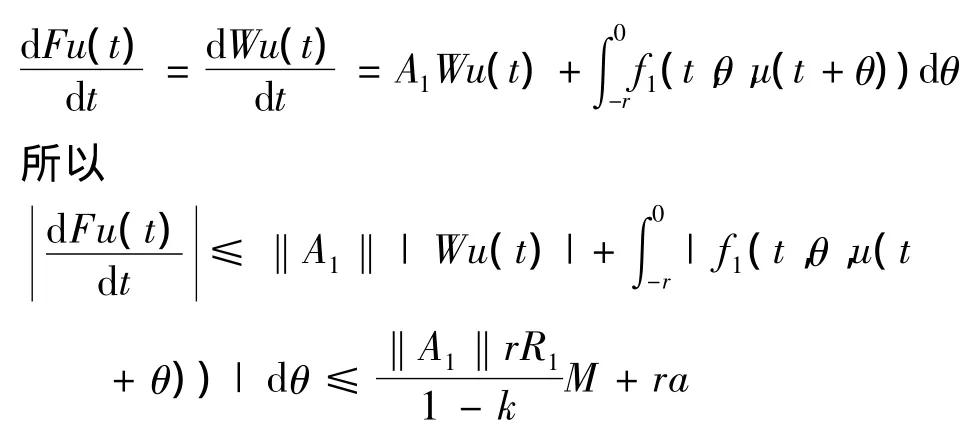
②证明F在K上是紧的．即证FK是列紧的．

由K的定义及FK⊂K知，FK中的函数是一致有界的．下证FK是等度连续的．

由于

可见FK是等度连续的，由Arael˙a－Ascoli定理可得，FK是列紧的．即得F在K上是紧的．综上所述，F在K上是全连续的．

(3)证明G在K上为压缩的．

∀u1，u2∈ K，∀t∈[0，T]，由条件(2)可得

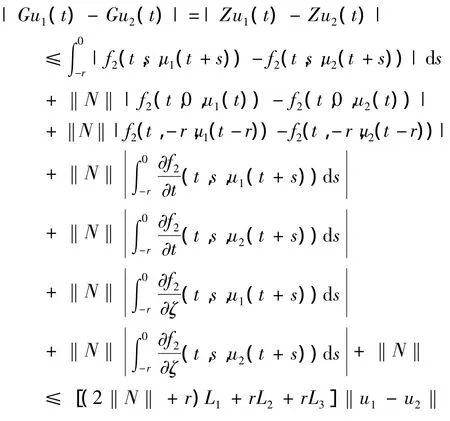
即

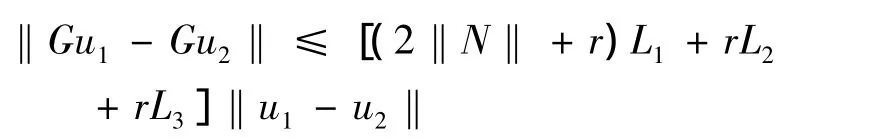
由于

[(2‖N‖ +r)L1+rL2+rL3]＜1

可知G在K上为压缩的．于是，由引理5可得，F+G在K上至少有一个不动点u*，u*即为系统(4)的T周期解．证毕．

[1] 周宗福，李蕾，王敬丰，胡秀林．一类退化中立型微分系统的周期解[J]．数学物理学报，2006，26A(7):1025－1030．

[2] 周宗福．一类具分布时滞的退化微分系统的周期解[J]．应用数学，2005，18(3):476 －483．

[3] Marz R．Some New Results Concerning Index－3 Differential－Algebraic Equations[J]．J．Math．Anal．Appl，1989，140(1):177－199．

[4] 蒋威．退化、时滞微分系统[M]．合肥:安徽大学出版社，1998．

[5] 彭世国，朱思铭．具有无穷时滞泛函微分方程的周期解[J]．数学年刊，2002，23A(3):371 －380．

[6] 周宗福，郑祖庥．非线性退化时滞系统的周期解[J]．系统科学与数学，2003，23(1):43 －50．