半鞅的极大值不等式①

冯德成， 陈彩龙， 蒋文君

(西北师范大学数学与统计学院，甘肃兰州730070)

0 引言

本文用 X1，X2，… 或 S1，S2，… 表示定义在固定的概率空间(Ω，F，P)上的随机变量序列，X+=max(0，－X)，I(A)表示集合A上的示性函数．

定义1 设S1，S2，…是L1随机变量序列，如果对任意的j=1，2，…都有

E{(Sj+1－ Sj)f(S1，…，Sj)}≥0 (1)其中f是任一使上述期望存在且对每个变元均非降的函数，则称{Sn，n≥1}为一个半鞅．此外，如果f是非负的，则称{Sn，n≥1}为一个半下鞅．

上述定义首先是由Newman和Wright提出来的，此后有很多学者对半(下)鞅进行了研究(如文献[1]－[9]等)．

而本文将文献[1]中关于半鞅的极大值不等式的结论进行了改进和推广，并得到了该不等式的一些应用．

1 主要结果及证明

定理1 设{Sn，n≥1}是半鞅，h(·)是一个不减函数，{ck，k≥1}是一正数序列，若函数g(·)满足g(0)=0，且对∀x，y∈R，有g(y)－g(x)≥(y－x)h(x)且(ck－ck+1)g(Sk)≥0，k≥1，则对∀ε ＞ 0，有

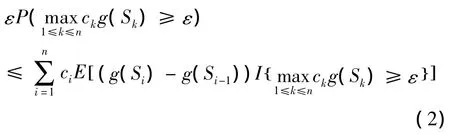
证明: 令m(·)为R上的非负不减函数，且m(0)=0，定义Sn'=max(c1g(S1)，cng(Sn))，S0'=0．由于

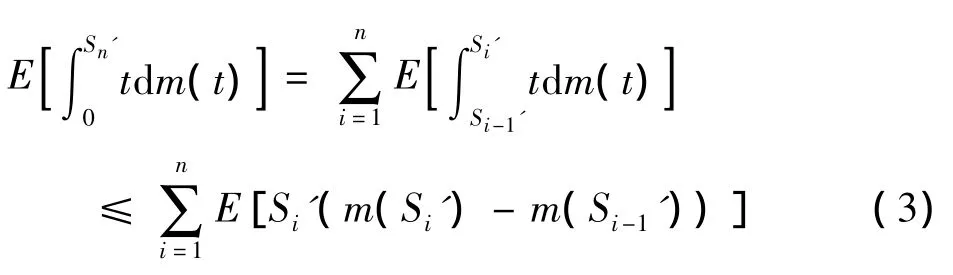
由Sn'的定义知，S1'＜0则m(Si')=0，而且当 Si' ＞ Si－1'有 Si'=cig(Si)，m(Si')=m(Si－1')，因此有

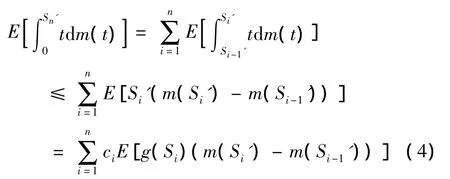
又因为 m(·)是 R上非负不减函数，Si'＞Si－1'，则

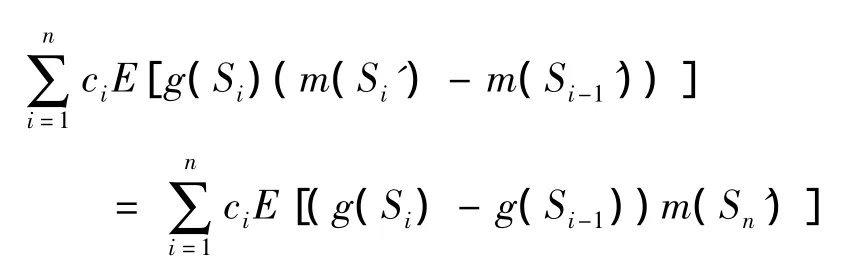
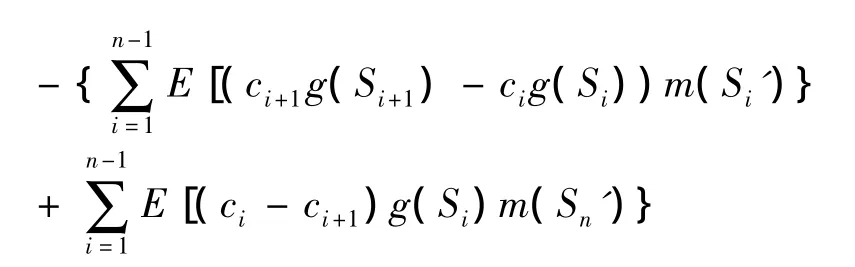
设

又因为(ck－ ck+1)g(Sk)≥0，k≥1，则

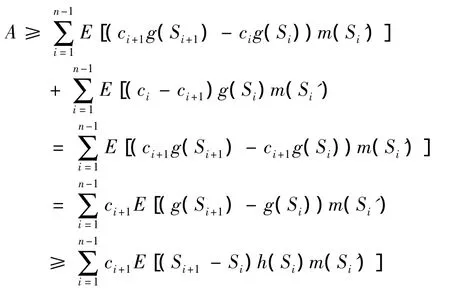
因为 g(·)满足g(0)=0，且对 ∀x，y∈R，有g(y)－g(x)≥(y－x)h(x)，h(Si)m(Si')是关于S1，…，Si的不减函数，由{Si，i≥ 1}是半鞅，则ciE[(g(Si)－ g(Si－1))m(Sn')]令 m(r)=I{t≥ ε}，则

三组学生网上收集“汶川地震17岁少年马健用双手救同学”的故事，谈谈勇气、坚毅、信心、意志和干劲是人的精神状态，如何理解“精神不是万能的，但没有精神是万万不能的”？

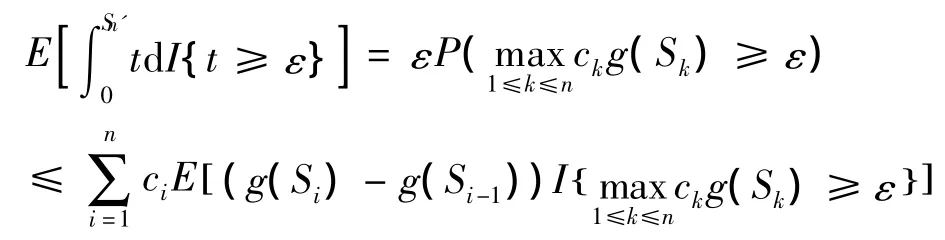
注 若令g(·)是一个凸函数，h(·)是函数g(·)的左导数函数，即

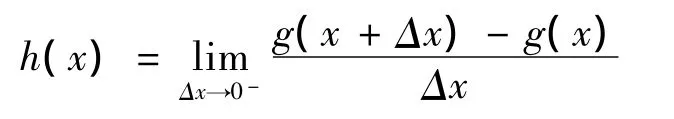
则h(·)是不减函数，且满足

g(x)－g(x)≥(y－x)h(x)

此时定理1则为文献[1]中的定理2．1．

定理2 设{Sn，n≥1}是半鞅，h(·)是一个不减函数，{ck，k≥1}是一正数序列，若函数g(·)满足g(0)=0，且对∀x，y∈R，有g(y)－g(x)≥(y－x)h(x)且(ck－ck+1)g(Sk)≥0，对p＞1，∀k≥1，都有E(g(Sk))p＜ ∞，则

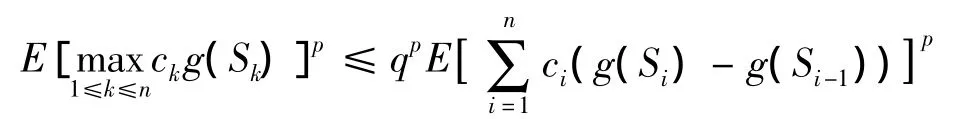
其中

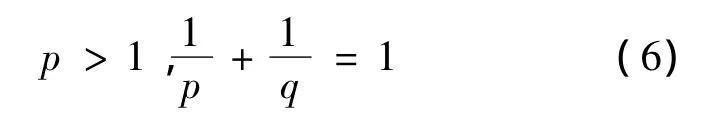
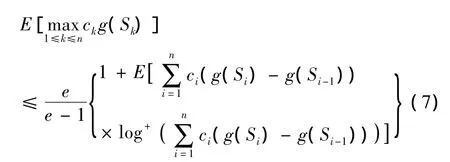
证明 由定理1，得

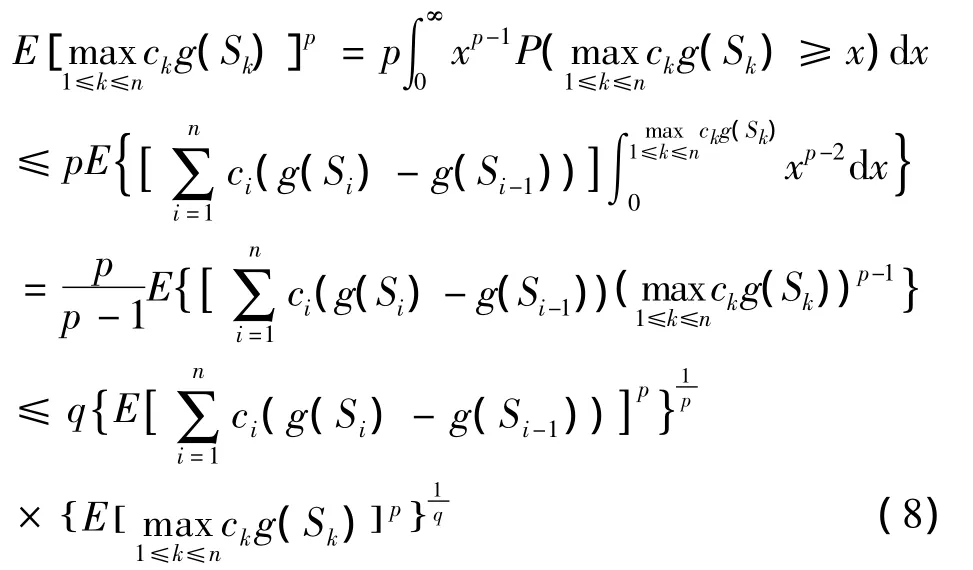
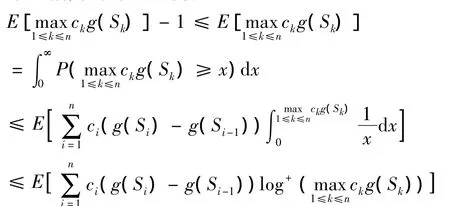
又因为 a≥0，b≥0，有alogb≤aloga++be+，则

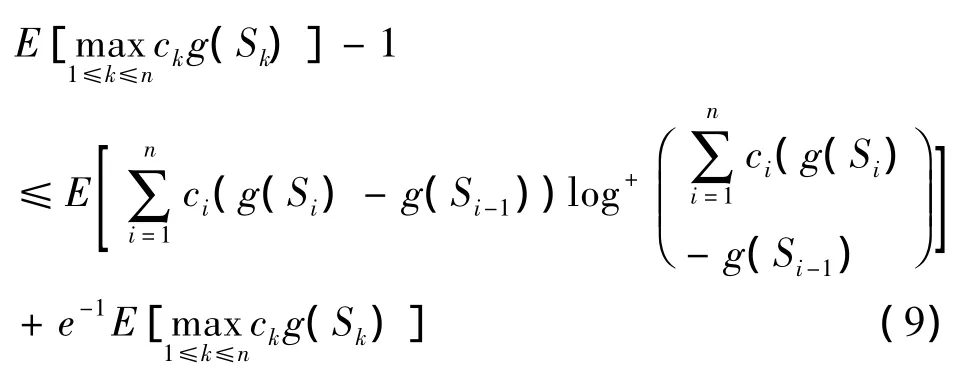
由(9)得到(7)．

推论1 设{Sn，n≥1}是半鞅，h(·)是一个不减函数，{ck，k≥1}是一正数序列，若函数g(·)满足g(0)=0，且对∀x，y∈R，有g(y)－g(x)≥(y－x)h(x)且(ck－ck+1)g(Sk)≥0，对p＞1，∀k≥1，都有E(g(Sk))p＜ ∞，则

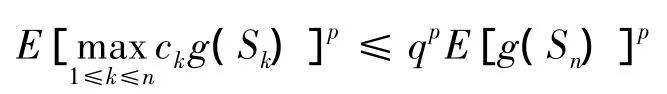
其中p＞1，

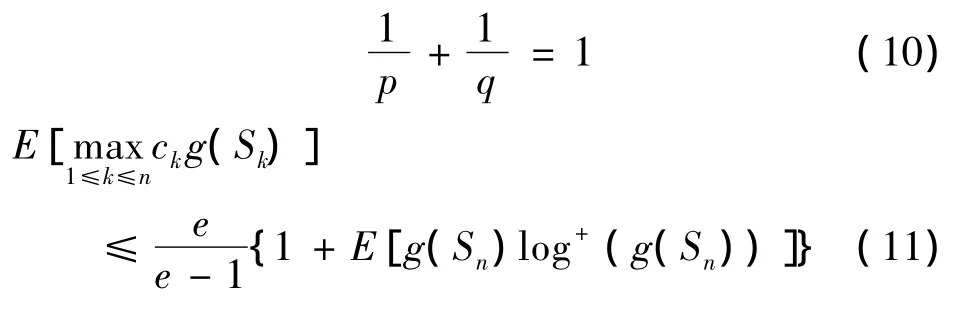
证明 由定理2，取ck≡1，则得(10)和(11)．

定理3 设{Sn，n≥1}是半鞅，h(·)是一个不减函数，{ck，k≥1}是一正数序列，若函数g(·)满足g(0)=0，且对∀x，y∈R，有g(y)－g(x)≥(y－x)h(x)且(ck－ck+1)g(Sk)≥0，∀k≥1，对0＜p＜1有

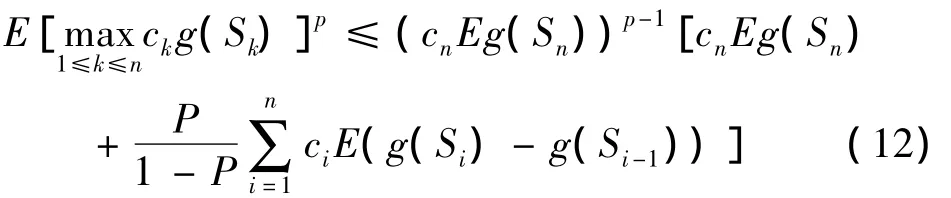
证明

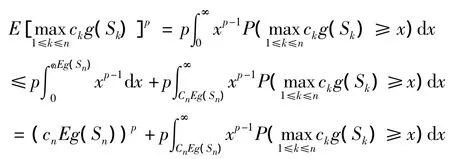
由定理1，得

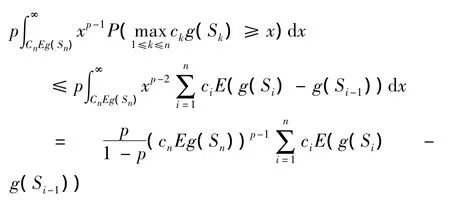
则(12)成立．

推论2 条件同定理1，则对k≥1，0＜p＜1，n≥1，有

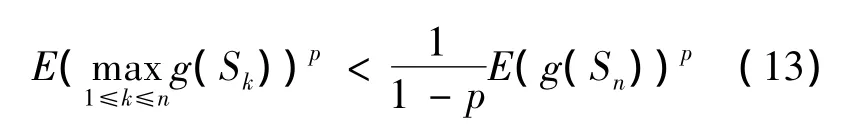
证明 由定理3，取ck≡1，则得(13)．

本文给出了半鞅的另一种形式的Chow型不等式，推广了文献[1]的结论．在此基础上，得到了半鞅的其它极大值不等式，并进行了一些应用．

[1] WANG Jian－ feng．Maximal Inequalities for Associated Random Variables and Demimartingales[J]．Statistics and Probability Letters，2004，3(66):347－354 ．

[2] Newman C M，Wright A L．Associated Random Variables and Martingale Inequalities[J]．Z．Wahrsch．Verw．Geb，1982，3(59):361－371．

[3] Newman C M，Wright A L．An Invariance Principle for Certain Dependent Sequences[J]．The Annals of Probability，1981，4(9):671－675．

[4] Tasos C．Christofides．Maximal Inequality for Demimartingales and a Strong Law of Large Numbers[J]．Statistics and Probability Letters，2000，50:357 －363．

[5] B．L．S Prakasa Rao．Hajek－Renyi －type Inequality for Associated Sequences[J]．Statistics and Probability Letters，2002 ，2(57):139－143．

[6] Hu，Shu－he，Chen，Gui－jing ，Wang，Xue－ jun．On Extending the Brunk－Prokhorov Strong Law of Large Numbers for Martingale Differences[J]．Statistics and Probability Letters，2008，78(18):3187－3194．

[7] WANG Xue－jun，HU Shu－he．Maximal Inequalities for Demimartingales and Their Applications[J]．Science in China Series A:Mathematics，2009 ，10(52):2207－2217．

[8] Wang Xue－jun ，Hu Shu－He，Zhao Ting et al．Doob’s Type Inequality and Strong Law of Large Numbers for Demimartingales[J]．Inequalities and Applications，2010:11．

[9] Wang Xue － jun．，Prakasa Rao B．L．S．，Hu Shu － he et al．On Some Maximal Inequalities for Demimartingales and N－demimartingales based on Concave Young Function[J]．Journal of Mathematical Analysis and Applications，2012，2(396):434－440．

[10] Chow YS．A Martingale Inequality and the Law of Large Numbers[J]．Proceedings of the American Mathematical Society，1960 ，11:107－111．

[11] Fazekas I，Klesov O．A general Approach to the Strong Law of Large Numbers[J]．Theory of Probability and its Applications ，2001，45(3):436－449．

[12] Wang Xue－ jun，Hu Shu－he，B．L．S．Prakasa Rao．Maximal Inequalities for N－demimartingale and Strong Law of Large Numbers[J]．Statistics and Probability Letters，2011，9(81):1348－1353．

[13] Esary J D，Proschan F，Walkup D W．Association of Random Variables with Applications[J]．The Annals of Mathematical Statistics，1967，38:1466 －1474．