非线性和常规方法在求取异常下限中的对比研究①

董跃华

(成都理工大学数学地质四川省重点实验室，四川成都610059)

0 引言

地球化学异常下限的确定是勘查地球化学的一个基本问题，也是勘查地球化学应用与矿产勘查时决定成败的一个关键性环节[1]．一直以来，人们主要是使用常规的统计学方法来求取异常下限．如:概率格纸法、85%累频法、均值加标准离差法等．非线性分形理论能有效地克服传统统计方法的不足，它既能考虑到地球化学数据值的频率分布，也能体现地球化学数据的空间属性，同时又符合地球化学数据的非线性特征[2]．由于各种方法的局限性，还没有一种方法能够适用于所有的地质条件背景．这就需要根据地质背景数据来选择合适的方法．

1 常规统计分析方法

勘查地球化学数据中常用的统计分析方法主要有传统统计方法、累频方法和概率格纸法．

传统统计方法是以地球化学数据呈正态分布为基础的．当实际中数据不呈现正态分布时，需对数据进行预处理，即对数据中的极大/极小值进行剔除，然后以均值加上2倍标准离差做为异常下限．累频方法是把样本值小于或等于某个样本值的数据频率累加，即得到小于或等于该样本值的累积频率．一般使用累积频率85%时的样本值作为异常下限[3]．概率格纸法是将数据投影到概率格纸上，在格纸上的曲线上找到拐点，计算得出背景部分累计频率所对应的横坐标，就是异常下限．

2 非线性统计方法－分形含量面积法

分形含量面积法首先根据地球化学采样数据的空间位置以及含量变化构建地球化学含量曲面，然后改变度量尺度来求取对应的曲面的面积，最后通过最小二乘法拟合确定地球化学异常下限[4～6]．

3 实际应用

以谢通门地区为例，其土壤地球化学测量采样点共 415 个，对采样点中的 Cu，Au，Ag，Pb，Zn 等五种元素进行分析，其特征统计量如表1，用不同方法分别求取五种元素的异常下限，如表2．

表1 各元素特征统计量

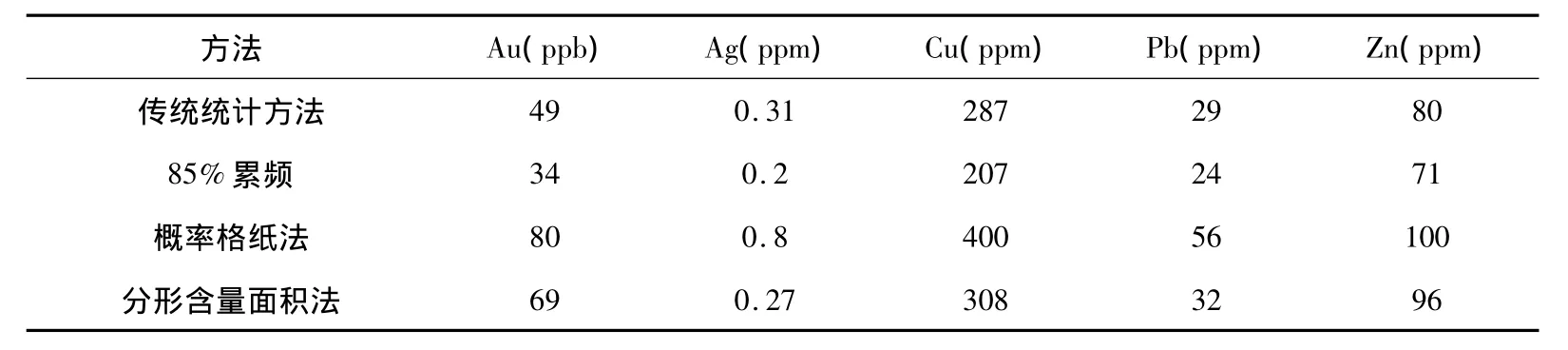
表2 各元素采用不同方法确定的异常下限值

研究区域主要是铜金矿区，现在对Au元素进行分析讨论，Au元素原始数据直方图与原始数据对数直方图如图1～图2．根据表2中统计出的异常下限值，通过Mapgis软件将其异常图绘制出来，如图3～图6．

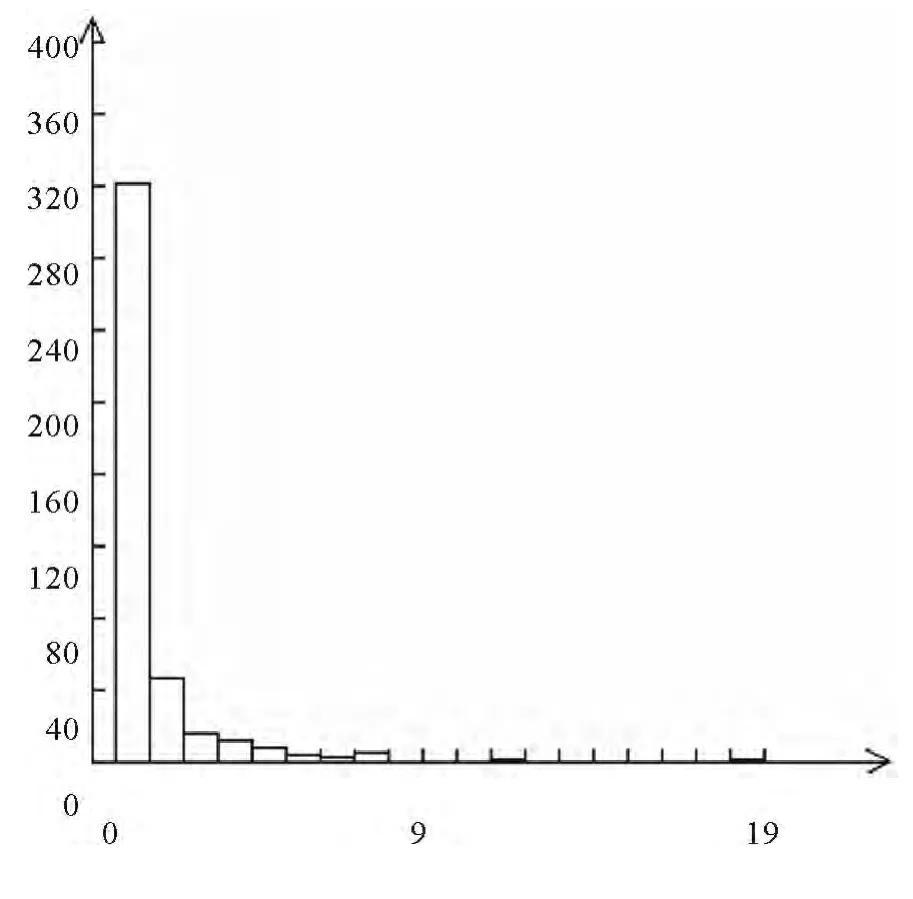
图1 Au元素原始数据直方图

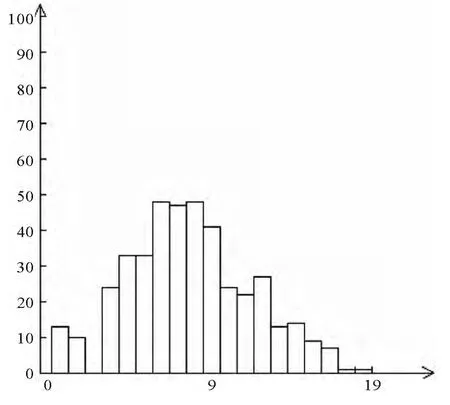
图2 Au元素原始数据对数直方图

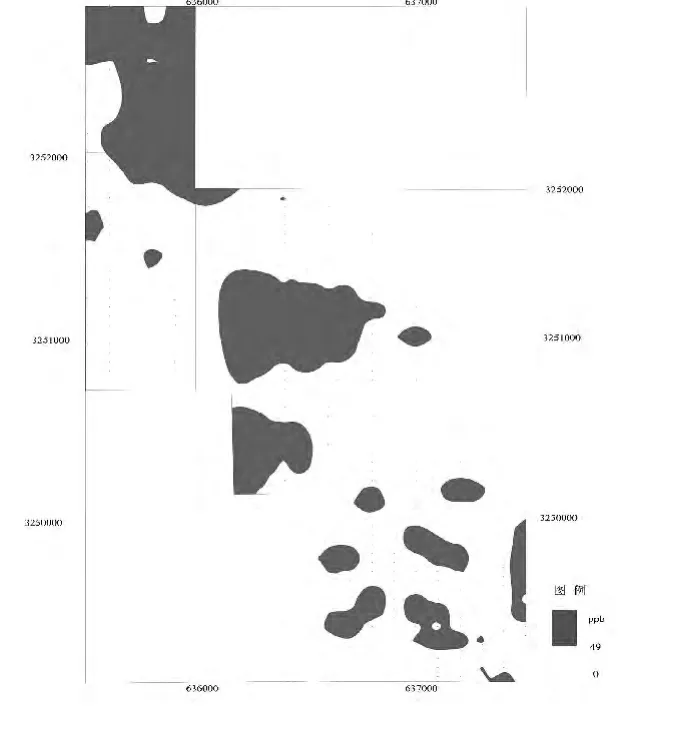
图3 传统统计方法异常图

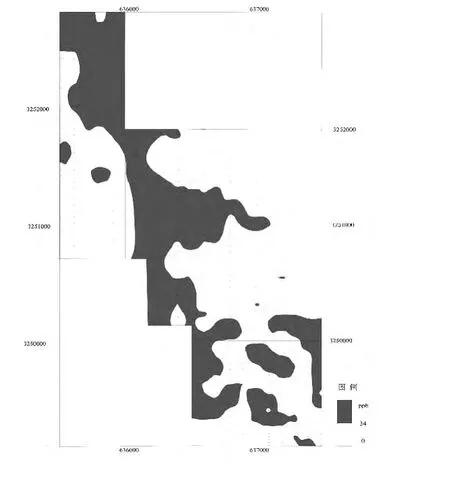
图4 85%累频方法异常图

图5 概率格纸法异常图

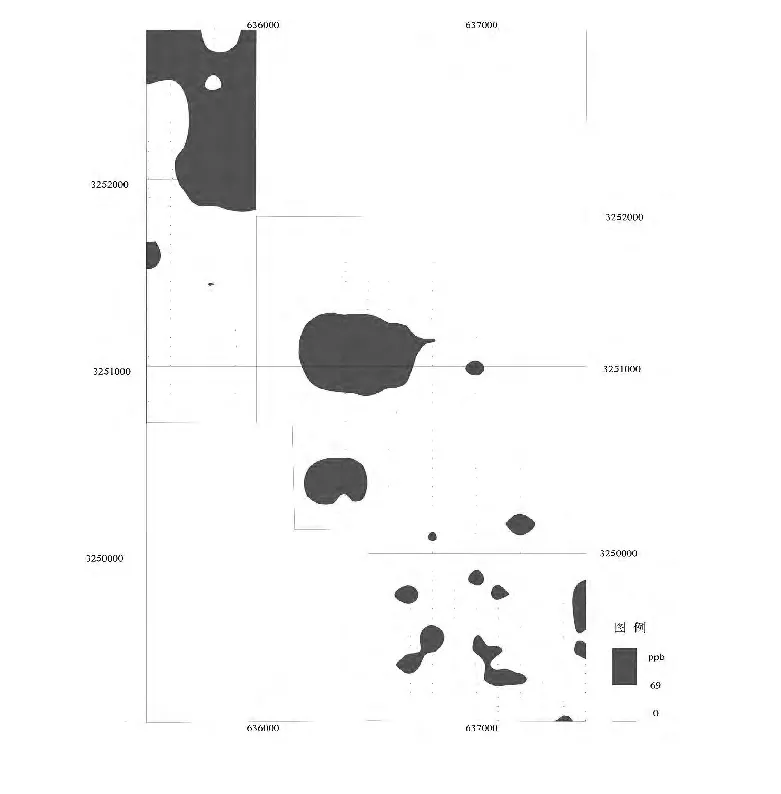
图6 分形含量面积法异常图

从表2中可以看出，85%累频确定的异常下限最低，而概率格纸法所确定的异常下限值最高，含量面积法所确定的异常下限相比于传统统计方法有时高有时低，是因为它在处理数据的过程中是对所有数据进行的处理，会有特高值和特低值的影响，而传统统计方法在进行数据处理时是经过数据筛选过的．

通过以上四种方法绘制的异常图，可以发现概率格纸法和分形含量面积法所圈定的异常范围基本一样．累频法所圈定的异常面积比较大，约占通体的1/3左右．总体来讲，通过以上方法能基本确定Au元素的空间分布特征，并且经后期工程验证，传统统计方法和累频法与圈定的元素异常区域基本相符，但累频法所圈定的范围太大，相比与传统方法，其实际工作量将大大增加．

4 结论

谢通门地区的Au元素含量服从对数正态分布，概率格纸法与分形所圈定的异常范围基本一样，但是无法将一些异常区域完全凸显出来，传统统计方法和85%累频法可以将异常区域很好的反映出来，但若依据85%累频法来进行地质勘测，需要很多的人力物力．以此看来传统统计方法在处理数据服从正态分布或对数正态时，效果更好．

[1] 郭科，魏友华，陈聆，等．基于MAPGIS平台下分形理论在地球化学异常圈定中的应用[J]．成都理工大学学报，2006，33(4):356－359．

[2] 孙忠军．矿产勘查中化探异常下限的多重分形计算方法[J]．物探化探计算技术，2007，29(1):54．

[3] 成秋明．多重分形与地质统计学方法用于勘查地球化学异常空间结构和奇异性分析[J]．地球科学－中国地质大学学报，2001，26(2):161 －167．

[4] 成秋明．多维分形理论和地球化学元素分布规律[J]．地球科学，2000，25(3):311 －317．

[5] 汪伟，张颖慧，袁峰，等．基于分形方法确定合肥大兴地区土壤中Cd元素的异常下限[J]．环境科学与管理，2009，34(5):27－30．

[6] 柳炳利，郭科，王维，等．非线性地球化学矿化元素组合求异方法在西藏洞噶普矿区的应用[J]．地学前缘，2012，19(2):256－265．