基于粒子群算法的平面刚架及组合结构的优化①

蔡保佩， 易平

(大连理工大学建设工程学部土木工程学院，辽宁大连116024)

0 引言

刚架[1]是目前较为广泛采用的一种建筑结构形式，在越来越多的建筑工程领域得到采用．刚架及其组合结构由于受力、内力复杂，截面自由度多等特点比桁架结构复杂的多，故对刚架的研究比桁架的研究要困难的多．近年来，随着钢结构使用的越来越广泛，针对刚架结构的优化问题，国内外设计和研究单位已经开展了一些研究工作，并取得了一些研究成果[1～2]．Haug 和 Arora[3]用矩阵力法对刚架进行优化研究，实现材料重量的最小化．朱伯芳[4]针对有应力约束的刚架问题，首先求出刚架的截面A、惯性矩I和截面模量W，进而通过整体分析得到各个构件的最大应力，最终完成刚架的有应力约束的优化．佟维[5]利用遗传算法．提出取刚架截面尺寸为设计变量，结构体积为目标函数，求全局最优解的概念．刘鹏[6]采用遗传算法，针对门式刚架，进行了包括离散和连续变量的截面形状混合优化，通过实例证明遗传算法应用于门式刚架的优化设计是可行的．吴科等[7]采用蚁群算法对3跨24层168根杆件的钢框架的结构质量进行优化计算，论证了蚁群算法在结构优化设计中的良好的实用价值．本文以刚架或刚架与桁架组合结构的截面尺寸为设计变量，在材料性质、荷载已知的情况下，进行有应力约束和位移约束的结构重量或体积最小化．主要利用了粒子群优化算法，并将其优化结果与改进的可行域算法(MMFD)、序列线性算法(SLP)、序列二次规划(SQP)等传统优化算法的结果进行比较．

1 粒子群优化算法简介

粒子群优化算法(PSO)是一种基于群智能方法的演化计算技术，于1995由Kennedy和Eennedy提出，算法模拟鸟群飞行觅食的行为，通过鸟之间的集体协作使群体达到最优．该方法初值由程序随机选取，群体解空间中追随最优粒子进行搜索，容易实现，同时又有深刻的智能背景，既适合科学研究，又特别适合工程应用[8～9]．

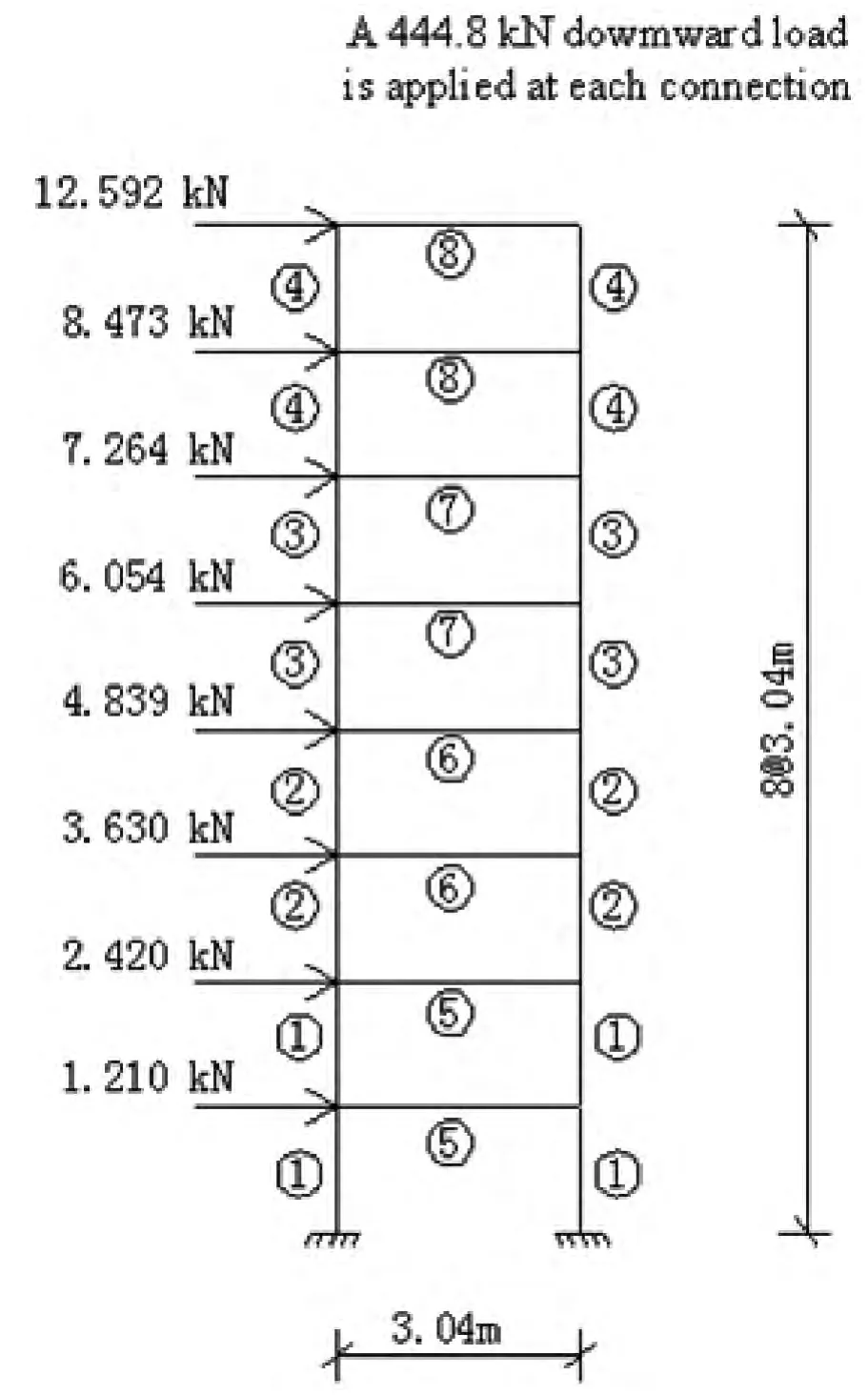
图1 八层刚架的结构计算简图

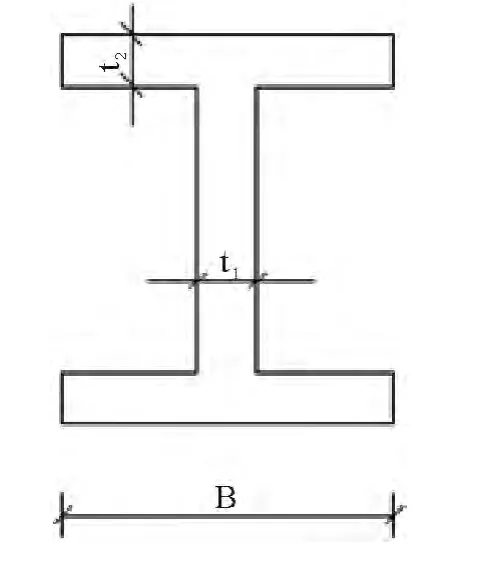
图2 型钢截面尺寸示意图

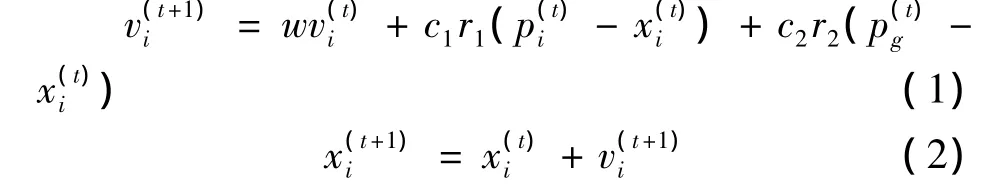
其中w为惯性权重，采用线性变化的惯性权重，c1，c2是正的实常数，称为加速因子，本文取为2．05;r1，r2为[0，1]中均匀分布的随机数[10～12]．本文PSO的计算参数选择如下:粒子群数ps=300，最大迭代次数T=400，c1=c2=2．05;

2 优化模型的建立及程序的运行步骤

刚架结构不仅要承受轴力、剪力，还要承受弯矩，截面受力复杂，本文利用求取最大应力．同时由于本文采用的有限元程序仅可计算出杆单元两端的轴力、剪力和弯矩，故在实际杆的两端、剪力为零处、集中力作用点、集中力偶作用点等处设置结点，从而有望求出整个刚架结构内的最大应力．

优化模型如下:

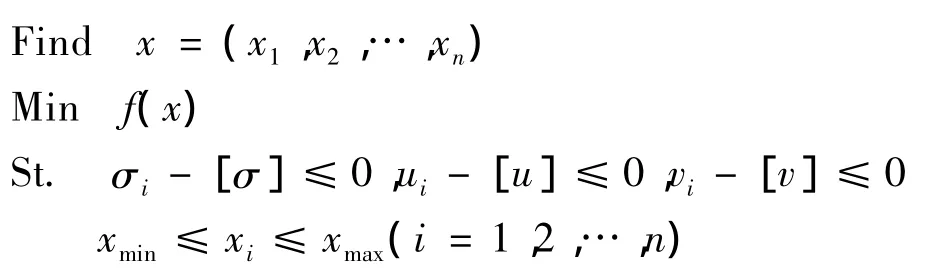
程序运行步骤如下:

(1)给定各设计变量初值(PSO不用给定初值，为随机取值);

(2)有限元程序读入各设计变量的初值;

我右手边的墙上是一个小女孩的关节造影，她的父母在那次车祸中双双辞世，她被推进手术室，诊断结果她右大腿肌肉坏死严重，只能高位截肢，我为她做了右髋关节离断术，这意味着她以后右腿将无法安装假肢。她的高烧不退，当我走到她的病床边，她问我，能否握着我的手睡觉，我点点头，她稚嫩的手指勾着我的手，手上还挂着一只小娃娃。她说见到小娃娃就好像见到了死去的爸爸妈妈，她不时地睁开眼确定我在她身边，才又睡去。

(3)有限元程序计算目标函数值、最大应力及最大位移;

(4)优化程序对最大应力、最大位移等约束条件进行检验，同时根据一定的寻优规则确定新的设计点;

(5)重复过程(3)和(4)，直至满足某项终止准则结束迭代．

3 算例

本文基于PSO算法依次对八层刚架结构、平面刚架与桁架组合结构进行尺寸优化．同时将所得结果与MMFD，SLP，SQP三种传统优化算法的结果进行比较．约束条件＞0．001视为违反约束，最大迭代次数均为100．

3．1 平面刚架结构的尺寸优化

如图1所示八层平面刚架，选自文献[13]．左侧结点均受一个大小如图示的集中力，同时每个结点均受一个大小为444．8 kN的集中力，各单元的弹性模量E=200GPa，材料密度为ρ=76．8 kN/m3，要求顶端位移不超过0．0508 m．选取各类截面面积为设计变量，截面面积分类如图1示，具有相同数字的各杆具有相同的截面面积．截面为H型截面，截面形式如图2所示，截面宽度B不得小于0．05 m，不得大于0．5 m，截面高度H不得小于0．1 m，不得大于1m，截面高宽比B/H不得小于1，不得大于10．优化结构使总重量最小．

本题中刚架为H型钢，截面比较复杂，故采用一定的简化措施[14]．腹板与翼缘的厚度选用经验公式

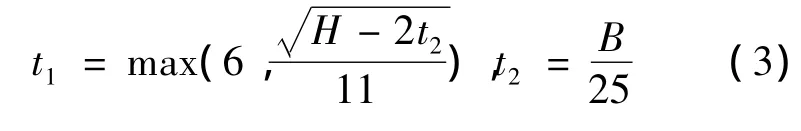
截面面积A的表达式为

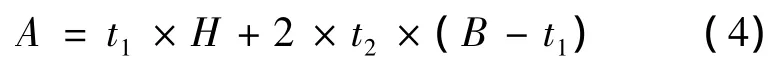
故设计变量仅剩下截面宽度B与截面高度H．

其优化模型可表示为:

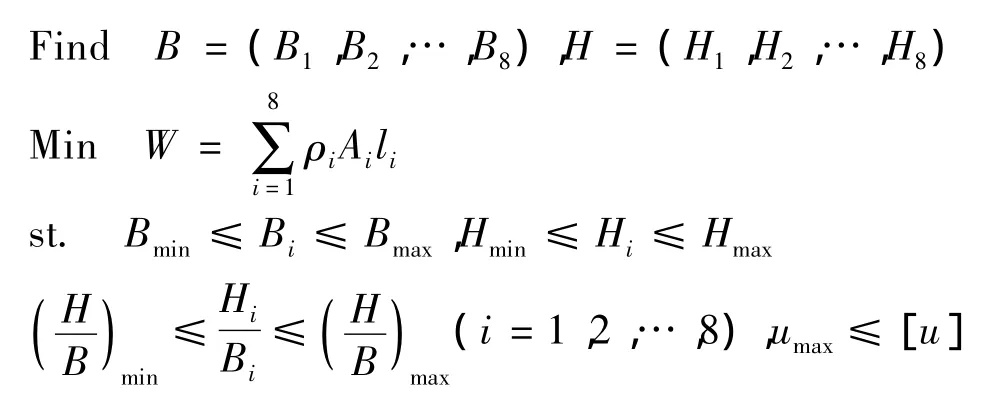
注意:式中li是结构中截面面积为Ai的各杆单元长度之和．

本算例分别使用四种不同的优化方法进行了五次优化，PSO算法初值五次均有由程序随机选取，三种传统算法的初值分别为:J1(最小值)、J2(最小值与最大值四分之一点处)、J3(最小值与最大值中点处)、J4(最小值与最大值四分之三点处)、J5(最大值)．四种不同方法五次优化的最终优化结果如表1所示:

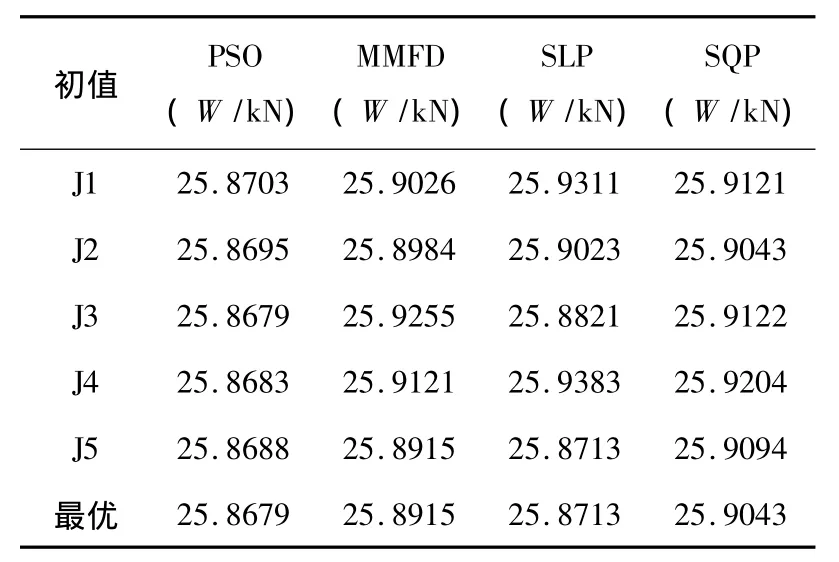
表1 八层刚架的不同方法优化目标值对比

由表1 可知，MMFD，SLP，SQP，PSO 算法的五次优化均能得到较好的可行解，但总体比较而言，PSO算法的五个结果更加接近，相对优于其他几种方法，充分说明了在八层刚架的优化过程中，PSO算法相对传统算法具有更强的稳定性．

针对不同方法在五次优化中选取最佳结果，其各个变量的对比如表2所示:

表2 八层刚架的不同方法最优结果对比

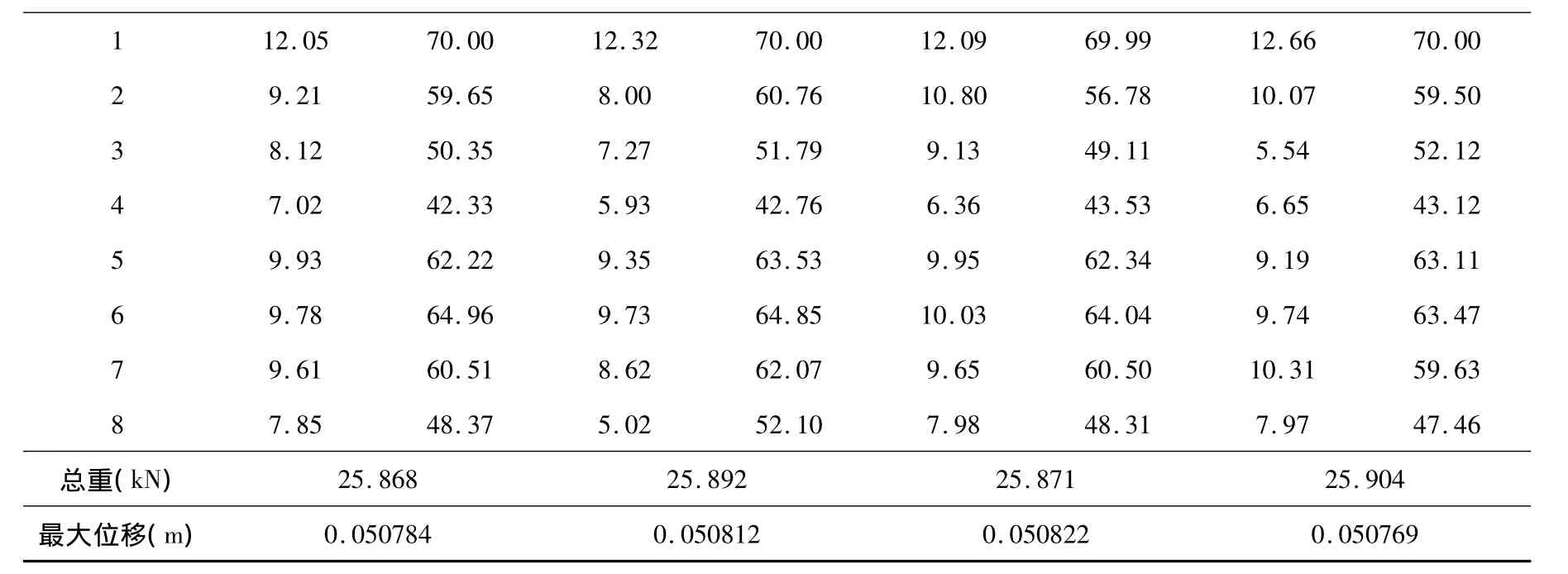
1 00 2 9．21 59．65 8．00 60．76 10．80 56．78 10．07 59．50 3 8．12 50．35 7．27 51．79 9．13 49．11 5．54 52．12 4 7．02 42．33 5．93 42．76 6．36 43．53 6．65 43．12 5 9．93 62．22 9．35 63．53 9．95 62．34 9．19 63．11 6 9．78 64．96 9．73 64．85 10．03 64．04 9．74 63．47 7 9．61 60．51 8．62 62．07 9．65 60．50 10．31 59．63 8 7．85 48．37 5．02 52．10 7．98 48．31 7．97 47．46 12．05 70．00 12．32 70．00 12．09 69．99 12．66 70．25．868 25．892 25．871 25．904最大位移(m)总重(kN)0．050784 0．050812 0．050822 0．050769

由表2可知，PSO，MMFD，SLP，SQP算法的最优结果均符合约束条件的要求，约束偏差均在0．001内，视为满足约束．同时比较四种算法的结果，PSO算法的总重量最小，充分说明了在八层刚架的优化过程中，PSO算法相较传统算法具有较好的收敛性．

同时文献参考文献[8]中也给出了优化的最终结果，并对其进行了型钢的选取，PSO算法先按连续变量求取最优解，然后参照型钢表选取型钢的结果与原文献结果对比如表3所示:

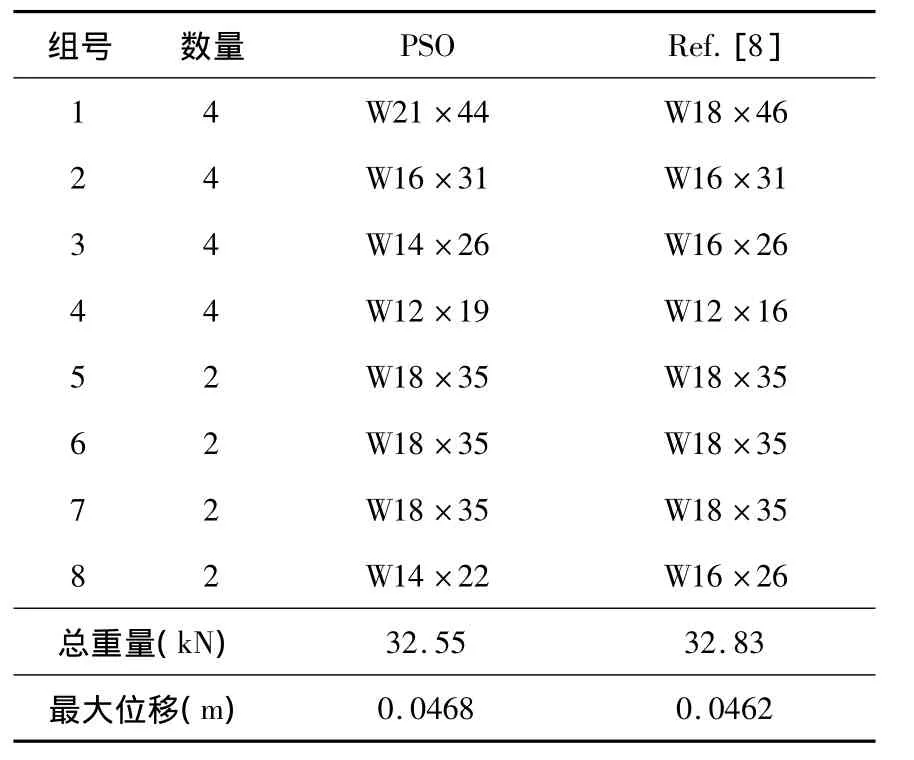
表3 选取型钢截面对比

由表3可知，通过PSO算法先按连续变量求取最优解，然后参照型钢表选取型钢，最大位移均在0．0508范围内，完全符合要求，同时用钢量比文献所用方法更加节省．充分说明了PSO算法在八层钢架优化过程中的正确性、有效性．

3．2 平面刚架与桁架组合结构的尺寸优化

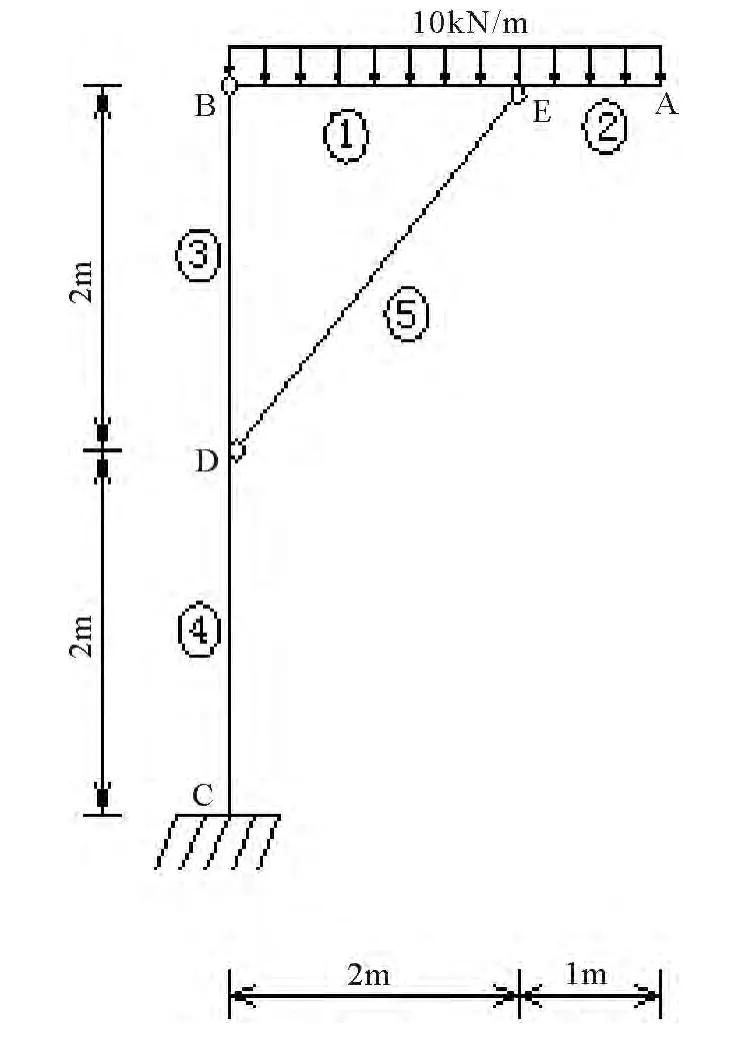
图3 组合结构计算简图

如图3所示组合结构，结构由相同材料组成，材料弹性模量E=210 GPa，许用应力为25 MPa．各节点的横向、竖向位移均不得超过0．02 m，选取各类截面面积为设计变量(图3中横梁1与2，立柱3与4分别采用相同的截面面积)，各杆截面面积不得小于1E－04 m2，不得大于6E－02m2，优化结构使总体积最小．

组合结构兼有桁架与刚架的性质，在现实中的应用十分广泛．结构中有一部分杆只承受轴向力，一部分杆却受力复杂，图2中横梁1上有弯矩最大点，选取该点及各杆杆端为结点，该结构结点的序号、杆的序号以及各自的自由度如图4所示．

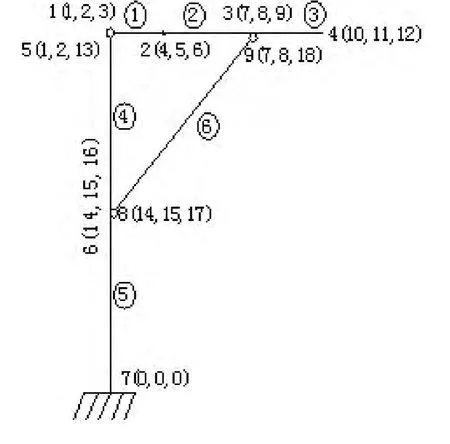
图4 组合结构结点及结点自由度示意图

其优化模型可表示为:

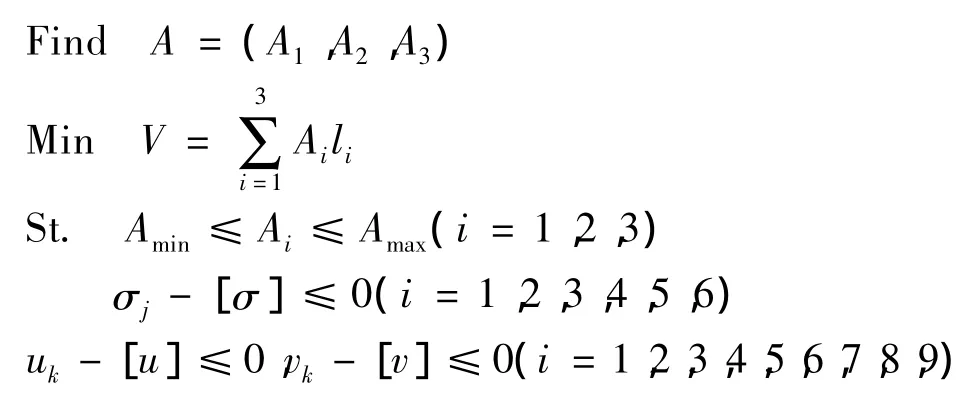
注意:式中li是结构中截面面积为Ai的各杆单元长度之和．

和例题1一样，本算例也分别使用四种不同的优化方法进行了五次优化，其最终优化结果如表4所示:

表4 组合结构不同方法目标值对比

注意:“－”代表局部收敛，“×”代表违反约束

由表4可知，SLP算法在初值取J3时得不到可行解，SQP算法在初值取J2、J4时不能得到可行解，在初值取J5时陷入局部收敛，而PSO算法的五次计算均能得到可行解，且五个结果都很接近，充分说明了在平面刚架与桁架组合结构的优化过程中，PSO算法相对传统算法具有更强的稳定性．针对不同方法在五次优化中选取最佳结果，其各个变量的对比如表5所示:

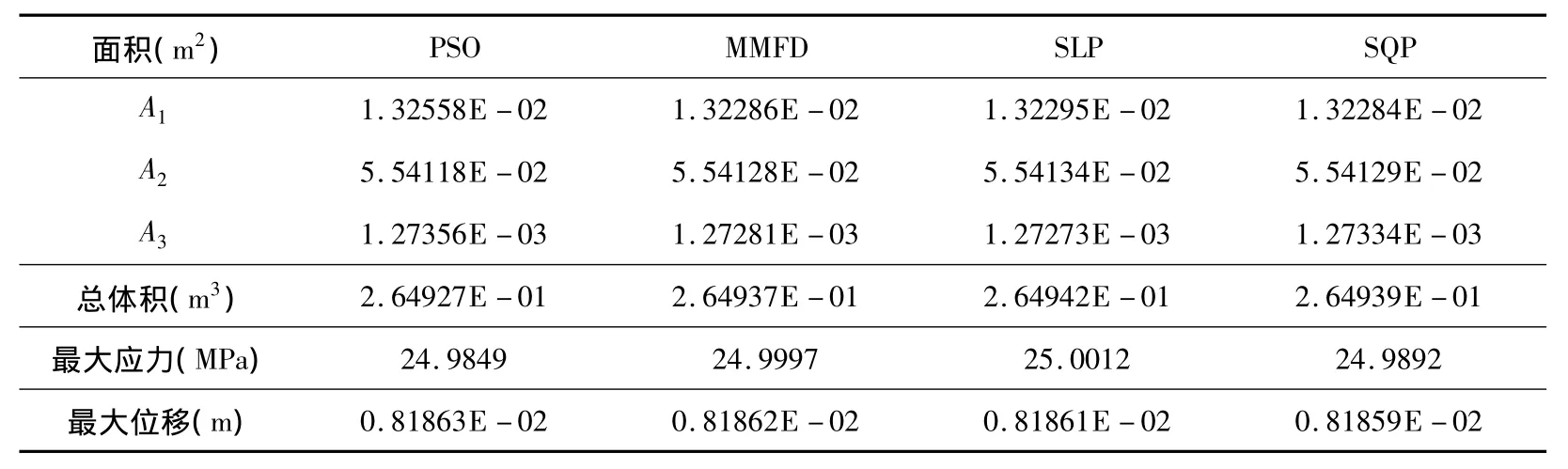
表5 组合结构不同方法最优结果对比

由表5可知，PSO，MMFD，SQP算法的最优结果均符合约束条件的要求，最大应力约束偏差均在0．001内，最大位移远远满足约束，视为应力约束、位移约束均得到满足．充分说明了在平面刚架与桁架组合结构的优化过程中，PSO算法具有很好的收敛性．

4 结论

本文运用粒子群优化算法实现了平面刚架结构及组合结构的优化设计，同时运用MMFD，SLP，SQP等传统算法进行优化结果的比较，主要结论如下:

(1)平面刚架结构及平面组合结构由于受力、内力更复杂，故其优化相对桁架结构要复杂的多;而粒子群优化算法可以较好地解决平面刚架及平面组合结构的尺寸优化问题;

(2)粒子群优化算法相对传统优化算法MMFD，SLP，SQP有更好的全局收敛性与稳定性，其优化结果不依赖于初值的选取，可以更加有效地避免局部收敛，于现实工程更有意义．

[1] 汪洋．门式刚架轻型钢结构优化设计研究[D]．杭州:浙江工业大学，2006．

[2] 冯建霖．门式刚架轻钢结构优化设计研究[D]．西安:西北建筑科技大学，2009．

[3] Haug E J，Arora J S．Applied Optimal Design:Mechanical and Structural Systems[M]．New York:Wiley，1979．

[4] 朱伯芳．结构优化设计原理与应用[M]．北京:水利水电出版社，1984．

[5] 佟维．利用遗传算法的结构优化设计[J]．大连铁道学院学报，2000，21(2):7－11．

[6] 刘鹏．门式刚架优化设计[J]．工业建筑:2001(7):58－60．

[7] 吴科，李哲，赵岩峰，等．基于蚁群算法的刚架结构优化设计[J]．钢结构，2007，22(6):13 －16．

[8] Eberhart R C，Shi Y．Particle Swarm Optimization:Developments，Applications and Resources[C]．//Evolutionary Computation，2001．Proceedings of the 2001 Congress on．IEEE，2001(1):81－86．

[9] Parsopoulos K E，Vrahatis M N．Recent Approaches to Global Optimization Problems through Particle Swarm Optimization[J]．Natural computing，2002，1(2 －3):235 －306．

[10] 王万良，唐宇．微粒群算法的研究现状与展望[J]．浙江工业大学学报，2007，35(2):136 －141．

[11] Poli R，Kennedy J，Blackwell T．Particle Swarm Optimization[J]．Swarm intelligence，2007，1(1):33 －57．

[12] 李宁，付国江，库少平，等．粒子群优化算法的发展与展望[J]．武汉理工大学学报(信息与管理工程版)，2005，30(02):26－29．

[13] Camp C，Pezeshk S，Cao G．．Optimized Design of Two－Dimensional Structures Using a Genetic Algorithm[J]．Journal of Structural Engineering，1998，124(5):551 －559．

[14] 陈绍蕃，顾强．钢结构基础[M]．北京:中国建筑工业出版社，2007．