交通事故下路段通行能力变化研究模型①

蒋梦曦， 杨 博， 刘凯旋

(1．重庆交通大学交通运输学院，重庆400074;2．重庆交通大学信息科学与工程学院，重庆400074)

0 引言

车道被占用是指因交通事故、路边停车、占道施工等因素，导致车道或道路横断面通行能力在单位时间内降低的现象．由于城市道路具有交通流密度大、连续性强等特点，一条车道被占用，其他车道的司机可能会减速瞭望占用的现场情况而使自身车辆的速度下降，同时被占用车道的车辆会转移到未被占用的车道，这些因素也可能降低未发生事故路段车道的通行能力，即使时间短，也可能引起车辆排队，出现交通阻塞．如处理不当，甚至出现区域性拥堵．车道被占用的情况种类繁多、复杂，正确估算车道被占用对城市道路通行能力的影响程度，将为交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案、设置路边停车位和设置非港湾式公交车站等提供理论依据．

目前，国内现有的方法如将公路通行能力乘以道路通行能力折算系数得到车道被占用情况下的通行能力[1]或则通过BP神经网络构建事故横断面实际通行能力模型[2]等．获取路段通行能力的主要方法主要有三种:第一种是通过实地调查，获取路段的实际通行能力，如美国《道路通行能力手册》[3]的研究;第二种是通过仿真研究，主要是通过仿真软件对道路通行能力的研究，如美国的TSIS、瑞典的VTI、德国的VISSIM等;第三种是通过一些相似情况下的模型，进行对比分析，找出两者的不同点与需要修正的地方来进行套用．前两种方法能够较为准确地获得路段通行能力，但是需要投入大量的人力、物力[4]．

因此本文将在现有研究成果的基础上，将交通事故下道路通行能力的计算模型与无信号管制的交叉口通行能力的计算模型进行了对比分析，从而得出了交通事故下通行能力计算模型，并通过实例分析了某城市道路交通事故发生前、发生时以及撤离后路段通行能力的变化情况，并分析其原因，证明了该方法的可用性．

1 交通事故发生前后路段通行能力变化

1．1 通行能力计算模型

假设研究路段内车辆的到达符合泊松分布，车辆间出现的时间间隔符合负指数分布，路段双向共有6条车道，即单向有3条车道，假设其中某条车道与相邻车道的车辆发生交通事故，并且完全占用两条车道．为了得到从交通事故发生至事故现场撤离完毕这期间，事故所处横断面实际通行能力的变化过程．可以采用如下步骤计算:

在事故发生时，利用最短车头时距t可以得到优先通行方向的交通量:

将无信号交叉口通行能力模型与交通事故下交通能力模型进行对比分析，可以得出两者的相似性．因为在无信号交叉口，如由东西方向直行的车行至交叉口处左转、右转与在交通事故下，相邻两条车道发生交通事故，这两条车道上的车辆全部转移到其余车道上的情况是相似的(如图1所示)．根据可插间隙理论[5]，直接计算优先方向交通流中的可插间隙(车头时间间隔)，即非优先方向交通可以横穿或插入的间隙数，作为非优先方向可以通过的最大交通量，从而得到交通量变化情况．我们把交通事故发生时占用的相邻的两条车道上的交通流作为非优先方向上的交通流，剩余的那一条条车道上的交通流作为优先方向上的交通流．

图1 无信号交叉口与交通事故发生道路车俩通行情况比较

因此，根据无信号交叉口通行能力计算公式:

从而计算出交通事故发生时所处横断面实际的通行能力:

对于事故发生前、事故撤离后每一条车道的实际能力计算，我们采用公式:

其中，C0为理想通行能力，其计算公式为，不同车道的t0取不同的值．fw，fcw，fFBIC均为实际道路通行能力修正系数．

fw为车道宽度修正系数;fcw为横向干扰修正系数;fFBIC为侧向净空受限的修正系数;t0为最小车头时距

Cr前，Cr后分别为事故发生前、后道路所有车道实际通行能力的总和．

Cr1，Cr2，Cr3，Cr1'，Cr2'，Cr3'分别为事故发生前后每条车道的实际通行能力．

根据(1)(2)(3)(4)(5)(6)可以计算出事故发生的前、中、撤离后的实际通行能力．从而得到在交通事故发生至撤离期间事故横断面通行能力的变化过程．

1．2 通行能力计算的实例分析

如图2所示为一条双向六车道的城市道路，单向交通量为Q，现在假设一次交通事故发生在车道二和车道三上且完全占用两条车道．当交通事故发生后，交通事故所占用车道上行驶的车将会全部转移到未被交通事故占用的车道上．城市道路的两条车道发生事故后，由于驾驶员观望甚至停车观望和其他的因素影响，剩余一条车道的通行能力也会下降．

本文数据来源于2013年全国大学生数学建模竞赛A[6]，道路上的电瓶车、行人作为道路干扰条件处理．

事故实例分析

如图2所示为一条双向六车道的城市道路，交通量为Q，现在假设交通事故发生在车道二和车道三上，当交通事故发生后，交通事故所占用车道上行驶的车将会全部转移到未被交通事故占用的车道上．

图2 交通事故发生路段情况示意图

根据视频一，可以得到事故发生前、中、后的最短车头时距，数据见表1所示．

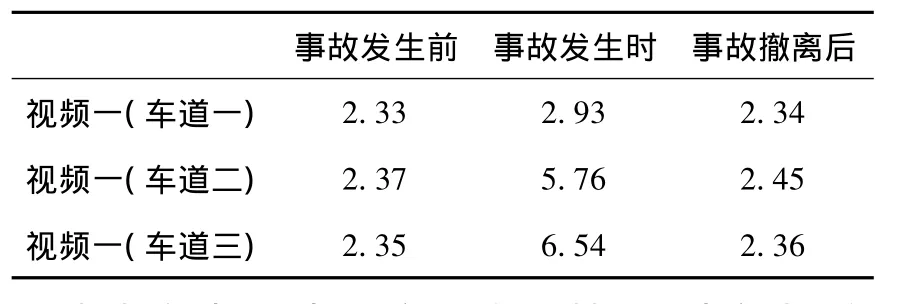
表1 各时段对应车道的最短车头时距(s)

根据视频一中的实际交通情况，查阅相关道路条件修正系数[7]，最外侧的车道(车道一)受到的横向干扰较大同时侧向净空受限，因此车道一中:fw=0．96，fcw=0．85，fFBIC=0．81．而车道二和车道三中均取:fw=0．96，fcw=0．94，fFBIC=0．92．其中，t=2，93s，tc=6s．

由公式(1)(2)(3)(4)(5)(6)以及表1中各时段车道的最短车头时距分别计算出各时段的实际通行能力，见表2．

表2 各时段事故断面实际通行能力(pcu/h)

可以看出，发生交通事故，事故断面的实际通行能力明显下降，是因为只剩下一个可通行车道，通行能力当然迅速下降．由于交通需求量大于实际通行能力，所以会造成拥堵，事故撤离后，道路实际通行能力又上升了，且事故撤离后道路的实际通行能力与道路，事故发生前的实际通行能力相差不大．

2 结语

本文利用无信号交叉口的通行能力与交通事故下道路的通行能力进行对比分析，两者具有相似之处，由无信号交叉口的通行能力计算模型推导出了交通事故下道路通行能力计算模型．该通行能力计算模型能够较好的估算车道被占用时道路通行能力的变化情况，这将为交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案、设置路边停车位和设置非港湾式公交车站等提供理论依据．

[1] 陈岩，朱家明，姜聪等．交通事故下道路通行能力及排队长度的研究[J]．佳木斯大学学报，2013，31(6):880－883．

[2] 葛逊，赵小婷，时章强等．车道被占用对城市道路通行能力的影响[J]．上海商学院学报，2013，14(5):85－88．

[3] Highway Capacity Manual[M]．Higliway Research Board．Special Report 87．National Academy of Sciences．National Research Council．Publication 1328．Wasliington D C．2011．

[4] 牛世峰，姜桂艳．灾害条件下公路通行能力折算方法研究[J]．HIGHWAY，2013，3(3):128－132．

[5] 郭学琴，袁振洲．主路优先控制交叉口通行能力分析[J]．《山东理工大学学报(自然科学版)》，2006，(06):89－92．

[6] 2013年高教社杯全国大学生数学建模竞赛A题，http://www．mcm．edu．cn/．

[7] 李淑庆，李钰．交通工程导论[M]．北京:人民交通出版社，2010:121－122．