土石混合料压实特性的离散元分析①

程晓明， 郝培文

(1．天津市政工程设计研究院，天津300051;2．长安大学，陕西 西安710064)

土石混合料分布广泛，是一种优良的路基填料，常用于山区公路路基建设．由于粒径变化大，工程性质多变，因此在同一工程的不同路段、甚至同一路段的不同层位，土石混合料的标准干密度差别很大．高频率地校正土石混合料的标准干密度会严重阻碍施工的进度，给压实质量控制和检测带来诸多不便[1]．针对该问题很多学者提出了解决方法，但尚未形成系统的、可推广的体系，其中一个重要原因就是对影响土石混合料最大干密度的因素研究的不够深入．为此，本文借助离散元软件PFC2D对土石混合料振动压实试验进行模拟，探讨不同因素对土石混合料压实效果的影响，从而更好地指导工程实践．

1 PFC2D简介

二维颗粒流程序(PFC2D)理论基础是离散单元法(Distinct Element Method，DEM)，它将物理领域的颗粒实体抽象为数学领域的圆或球体，实物边界抽象为数学领域的多边形、多面体、柱体、球体等;颗粒间行为通过定义的接触模型实现;通过对实体边界施加力或速度来加载，进而实现颗粒集的力学特性分析．离散元法通过循环计算的方式跟踪颗粒圆的移动状况，每次循环包括两个计算步骤[2]:1)由作用力和反作用力确定颗粒间的接触作用力和相对位移;2)由牛顿第二定律确定颗粒间产生的新的不平衡力，直至达到要求的循环次数或者颗粒移动趋于稳定和平衡．

2 振动压实模型建立

模拟前应先生成颗粒体试样，通过控制颗粒间平均不平衡力与最大不平衡力的比值，使其达到重力平衡．然后，对试样施加循环力模拟振动压实过程，压实过程中通过记录试件密度、应力应变等参数随时间的变化情况来研究不同因素对压实效果的影响．

参照表面振动压实仪试筒尺寸，在280mm×250mm的矩形区域内生成级配颗粒，颗粒半径从Rmin到Rmax符合高斯分布．墙体刚度取颗粒刚度的0．1倍以降低边界效应影响[3]．为简化计算不妨设材料性质各向均匀，颗粒间呈线性接触(无黏聚力)，只通过摩擦系数fric、法向刚度Kn和切向刚度Ks来控制颗粒间行为．PFC2D软件不能直接对墙体施加力，因此采用28个半径为1cm的小球作为加载介质，球体间连接状态设为平行粘结模型(传递力和力矩，避免球体间滑动)．此外，设定球体角速度为0，使之不产生旋转．本文采用简化的简偕振动力模拟振动加载[4，5]．由于表面振动压实仪的激振力为80kN，频率为50Hz，振幅0．5mm简谐振动力为F=－[Acos(ωt)]，其中 ω=2πf=314;A=80kN．加载时设置加载力为F=－[Acos(ωt)]，负号表示力的方向向下．离散元数值模型如图1所示．

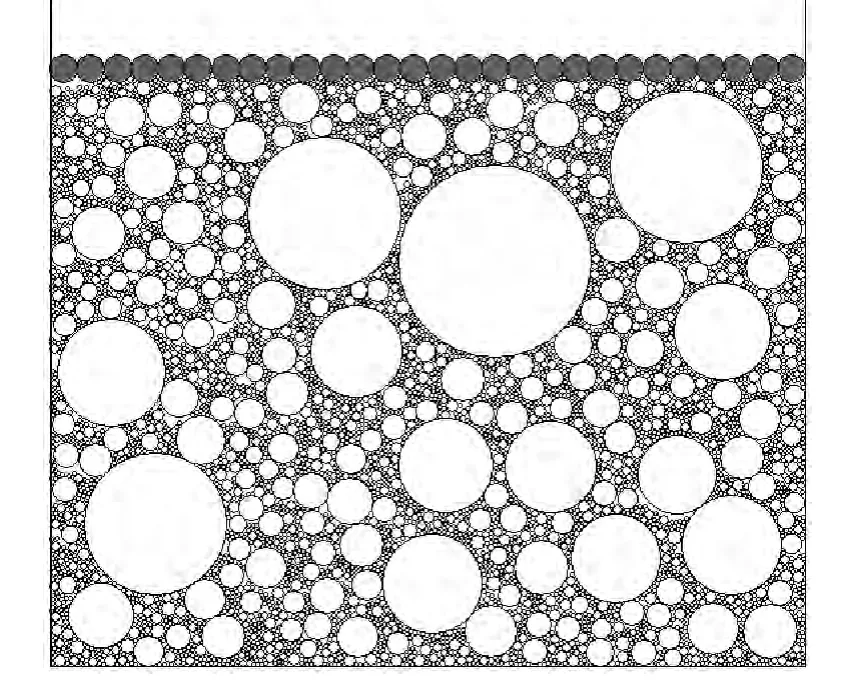
图1 颗粒体振动加载模型

生成的级配颗粒是否满足要求是模拟结果是否真实可信的关键．本文级配颗粒按如下步骤生成[4～6]:首先确定所有颗粒总质量．已知初始孔隙率和压实密度可由e=1－ρ/ρd反算颗粒初始密度(ρ，ρd分别为试样毛体积密度和压实密度)，在280mm×250mm容器中即可确定颗粒总质量．因此，不妨设初始孔隙率为15%，压实干密度2．5kg/cm3．求得总质量后，根据每档级配颗粒占的百分比可得到相应级配颗粒的质量，进而由n=∑m/(πρR2i)求得颗粒个数(ρ为级配颗粒密度，可试验测得)．为计算方便起见，R取每档级配的平均半径，计算结果n取整．

值得注意的是，随着粒径n变小，计算得到的颗粒数目越来越大．若颗粒数目超过1万，PFC2D软件的运行效率严重下降，甚至会出现程序无法响应、电脑死机等状况．为了提高计算效率，不妨将5mm以下的颗粒等量代换成1mm～5mm间的颗粒，经分析这种简化方法产生的级配误差可以忽略不计．

3 试验结果与分析

3．1 颗粒粗糙度影响效应

变化摩擦系数建立振动压实模型．从图2可以看出，初始状态下不同摩擦系数对应的密实度相差较小，随加载过程的进行，密实度差值越来越大．不难理解这种现象:石料越粗糙，达到相应密度需要克服的摩阻力就越大，需要的功也越多．加载初期应力应变曲线斜率有明显差别(如图3所示，负号表示受压):摩擦系数越小，曲线斜率越小．这同摩尔库仑定律反映的内容一致:模量反应了抵抗变形的能力，摩擦系数越小，斜率越小，抵抗变形的能力越差;而根据摩尔库仑定律，摩阻力越大，法向抗剪强度越高，抵抗变形能力越强．加载到中后期，应力应变曲线斜率逐渐减小．这说明颗粒粗糙度对加载初期的模量影响较大，填料粗糙度高的土石混填路基比材料粗糙度低的路基更加稳定．

图2 摩擦系数对密度的影响

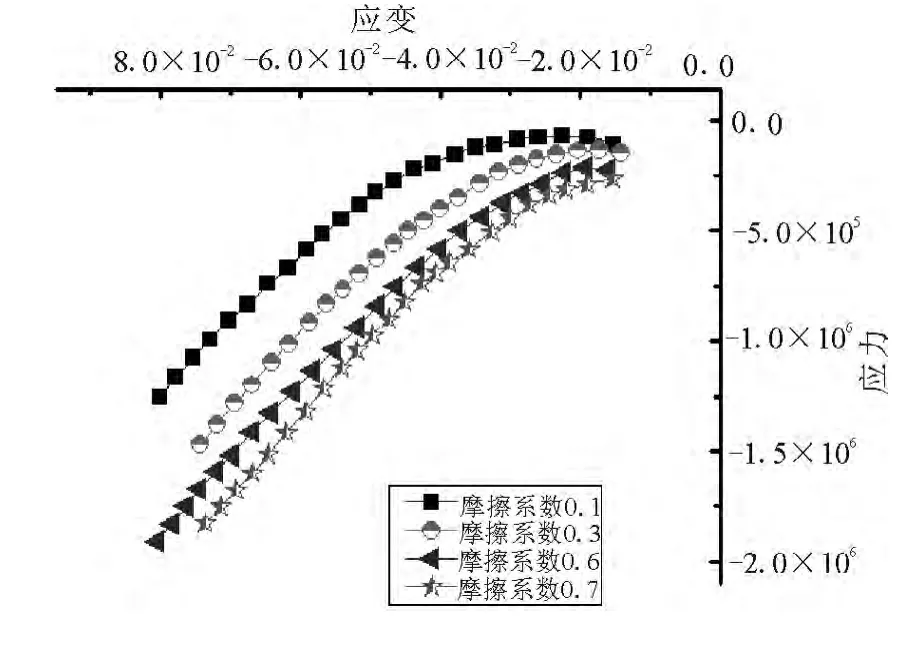
图3 摩擦系数对应力应变的影响

3．2 颗粒刚度影响效应

不同岩性的岩石，其破坏机制也有差异:在一定测压下，软岩表现为弱面破坏和塑性破坏，中硬岩石表现为剪切破坏，硬质岩石表现为脆性张裂破坏和剪切破坏．而土石混合料50%以上颗粒都是粗粒土或巨粒土，球体刚度直接反应石料性质，其含石量越大，球体刚度影响越难以忽略．

相同加载条件下，球体刚度越大密度越小(见图4)．可以理解为:土石混合料在加载过程中发生空间位置移动和自身形变．岩性不同，两者的主导地位也不同．硬岩颗粒刚度较大，导致密实度增加的主导因素是位移变化，颗粒位置重新排列;而软岩颗粒刚度较小，除了颗粒位移变化还发生自身形变，因此体积较硬岩小，密度较硬岩大．土石混合料本质是颗粒的集合，整体效应必然同颗粒本身相同．故颗粒刚度越大，相同加载时间下土石混合料的应力越大，应变越小，模量越大(如图5示)，抵抗变形的能力越强．整体来说，刚度对密度的影响较小，对模量影响则较为明显．

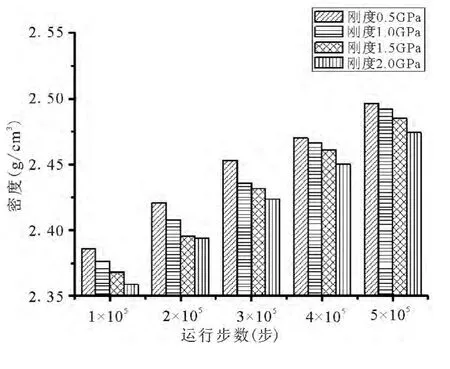
图4 颗粒刚度对密度的影响

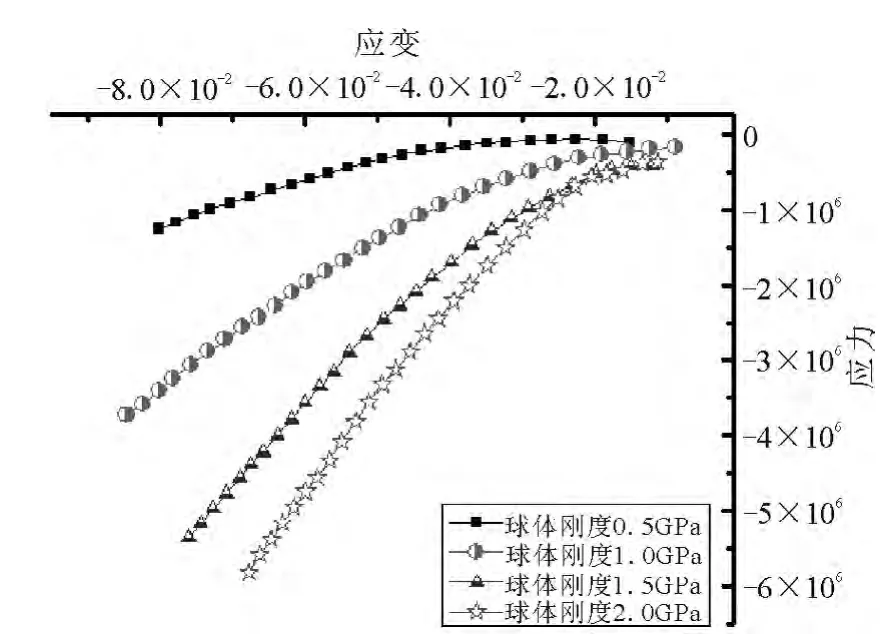
图5 颗粒刚度对应力应变的影响

3．3 最大粒径影响效应

大量室内试验显示，土石混合料最大粒径对密实度有较大影响．图6、图7是变化最大粒径建立振动加载模型得到的结果．由图可见:在相同的压实时间下，最大粒径越大，级配颗粒密度越大，模量越大．密度与粒径本身没有直接的相关性，而是与岩石类型有关．土石料是由暴露在地壳表面的岩石长期风化而成的，土石料形成过程中，主要受到地面水、氧气和二氧化碳等作用逐渐被溶解和氧化，变成松散的岩石和土壤．这个过程中，软岩较硬岩更容易风化，这就是粒径大的岩石其密度也大，粒径小的岩石其密度也小的原因所在．

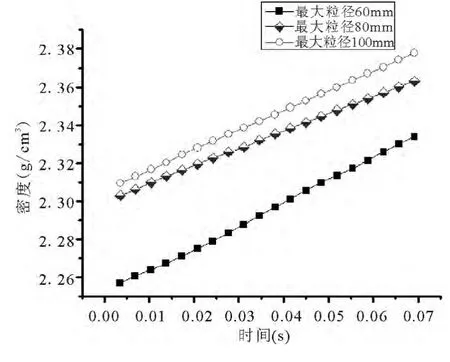
图6 不同粒径下密度随时间变化

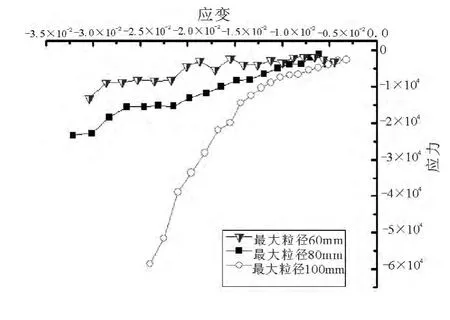
图7 不同粒径下应力应变随时间变化

3．4 含石量影响效应

为了研究不同含石量对密实度的影响，建立了不同含石量的振动加载模型进行分析对比．结果表明:含石量不同的试样其初始密实度不同，且含石量越大密实度越大(如图8)．含石量通过改变土石混合料的结构来影响土石料的密实度和模量的:含石量小于50%时，粗粒料悬浮在细料中，强度主要以颗粒间粘结力和填充力为主．含石量为60% ～70%时，混合土中粗料逐渐形成骨架，细料起填充空隙和胶结作用，强度由粗料骨架形成的嵌挤力和细料的胶结力共同组成，该类结构强度高，密实度也大．含石量超过80%以上时，骨架形成，细料不足，容易产生架空和粗料集中现象，密实度降低，粗粒料的嵌挤力是强度的主要来源．因此，一定范围内含石量大其模量也大(见图9)．

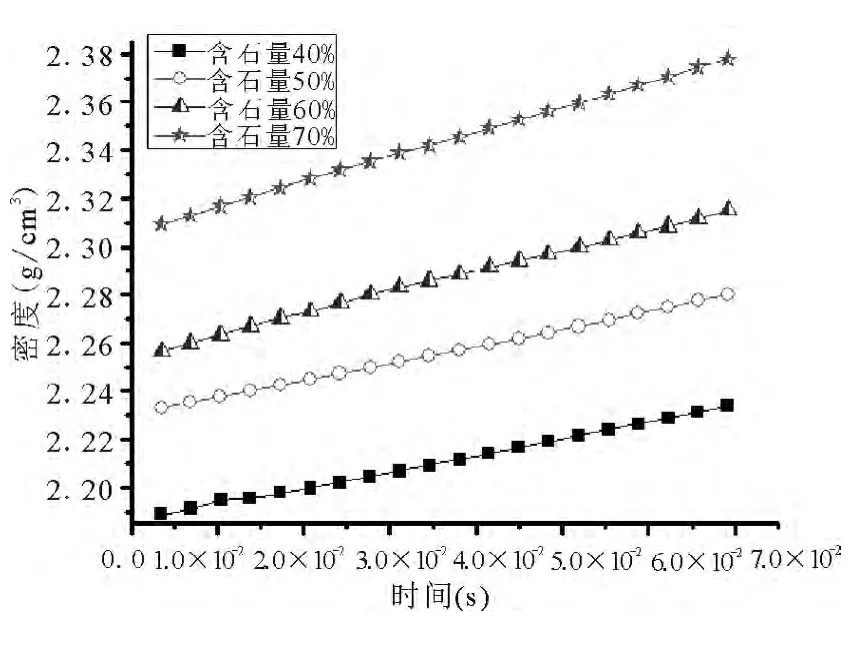
图8 不同含石量下密度随时间的变化

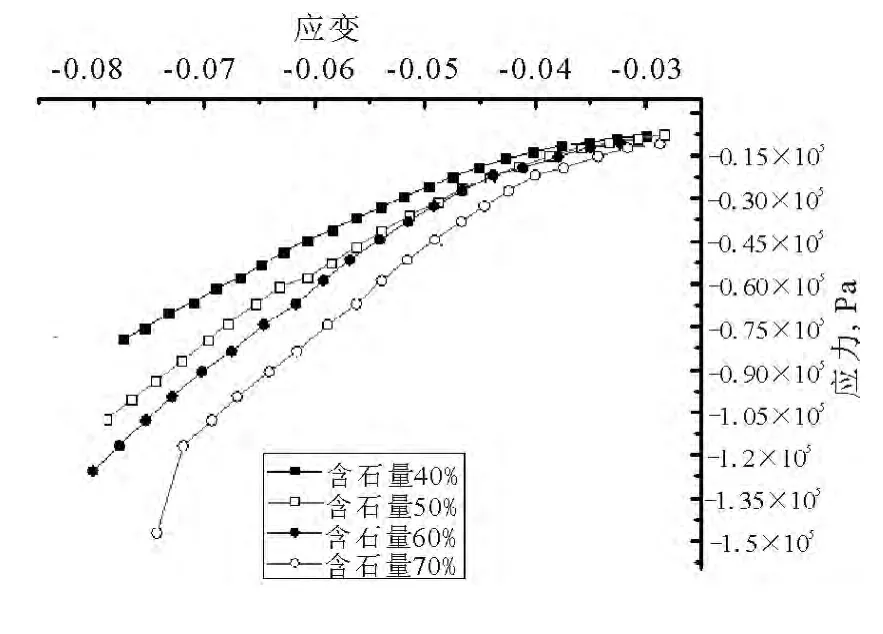
图9 不同含石量下模量随时间的变化

4 结论

(1)影响土石混合料压实度的内因主要有:颗粒粗糙度、颗粒刚度、最大粒径和含石量．(2)相同情况下，密实度与颗粒粗糙度、刚度成负相关性，与最大粒径、含石量成正相关性．模量与颗粒粗糙度、刚度、最大粒径、含石量均成正相关性．(3)从密实度随不同因素的变化增幅来看，宏观参数最大粒径、含石量对压实度的高低起主要作用，而微观参数颗粒粗糙度、刚度对压实度高低的作用较小．(4)以压实度为指标控制土石混填路基压实质量时，需要用最大粒径、含石量对标准干密度进行修正．

[1] 程晓明．土石混填路基压实特性与数值模拟[D]．陕西:长安大学，2012．06．

[23] 罗勇．土石问题的颗粒流模拟及应用研究[D]．杭州:浙江大学，2007，12．

[4] 蒋应军，任蛟龙，徐寅善等．级配碎石力学性能的颗粒流数值模拟方法[J]．同济大学学报，2011，39(5)．

[5] 孔祥臣，陈谦应，贾学明．土石混合料振动及时试验的PFC2D模拟研究[J]．重庆交通学院学报，2005，24(1):61 －66．

[6] Y．P．CHENG，Y．NAKATA and M．D．BOLTON．Discrete Element Simulation of Crushable Soil[J]．Ge techniques，2003，53，No．7:633–641．