航天器快速绕飞监测的相对姿轨耦合控制*

张庆展 靳永强 康志宇 肖余之

1.上海航天技术研究院航天运输与维护总体技术研究中心，上海 2011092.上海宇航系统工程研究所，上海 201109

航天器快速绕飞监测的相对姿轨耦合控制*

张庆展1，2靳永强1，2康志宇1，2肖余之1，2

1.上海航天技术研究院航天运输与维护总体技术研究中心，上海 201109
2.上海宇航系统工程研究所，上海 201109

研究了航天器空间任意方位快速绕飞与监测的相对姿轨耦合控制问题。通过合理绕飞参考系和期望姿态系的定义，将问题转化为绕飞参考系内的相对姿轨跟踪控制。通过设计航天器期望相对位置矢量和求取期望姿态运动规律，建立了符合航天器空间一般物理运动规律的相对运动与姿态指向模型，并给出相应控制律。仿真中以实现与目标轨道异面的快速圆绕飞为例，同时考虑绕飞航天器初始位置不在绕飞面的情况，设计了期望相对位置矢量的运动规律，并加入指数函数引导相对姿轨平滑过渡。考虑相对姿轨控制的强耦合性，绕飞航天器采用冗余推力器配置，并引入伪逆法实现控制指令的动态分配。最后针对示例的数值和可视化仿真验证了算法的正确性。

航天器;快速绕飞;监测;相对姿轨耦合控制;期望相对位置矢量

随着空间技术与应用的发展，航天器在轨服务已成为国际航天领域的研究热点。快速绕飞与姿态指向为航天器提供了短时间内快速在轨全方位探查空间目标的能力，在航天器的在轨检查和监测，空间目标识别与侦查等空间活动中具有重要作用。“快速绕飞”是较自然绕飞而言的概念，指绕飞航天器在控制力作用下，绕飞周期小于目标航天器轨道周期的环绕飞行。“监测”指在航天器间的相对运动中，控制航天器的姿态使其敏感轴始终保持指向目标航天器或目标区域。实现对目标航天器或目标区域全方位的快速绕飞监测，需要对绕飞航天器进行姿轨耦合控制。其耦合性主要体现在2方面:1)期望姿态指向由相对位置决定;2)共用推力器同时实现姿态和轨道控制。文献［1］基于四元数研究了编队飞行中姿态指向控制问题。文献［2］给出了连续小推力条件下的一种快速圆编队设计方法。文献［3］研究了多脉冲控制的快速圆绕飞轨迹优化问题。文献［4］以圆绕飞为例，给出了任意方位快速绕飞轨迹数学表示和期望姿态计算模型。文献［5］在相对运动T-H动力学基础上研究了快速绕飞姿轨的协同控制问题，在绕飞轨迹规划中未考虑初始位置不在绕飞面的过渡问题。上述内容主要是针对特定目标的姿态指向或者特定绕飞轨迹的设计方法进行研究，尚未见到针对空间一般相对运动与姿态指向问题的研究。

本文从符合航天器空间一般物理运动规律的相对运动与姿态指向入手，通过合理绕飞参考系和期望姿态系的定义，将航天器任意方位快速绕飞监测控制转化为绕飞参考系内相对姿轨跟踪控制。首先，以面向任务需求的设计思想，在绕飞参考系内设计绕飞航天器相对目标的期望相对位置矢量，并建立绕飞航天器的期望姿态运动规律。然后，构建基于期望相对位置矢量的相对姿态轨道动力学方程，并给出控制律。最后，针对与目标轨道异面的快速圆绕飞监测进行仿真，并考虑绕飞航天器初始位置不在绕飞面的过渡问题，加入指数函数引导相对姿轨平滑过渡。考虑相对姿轨控制的强耦合特性，绕飞航天器采用冗余推力器配置，引入伪逆法实现控制指令动态分配，并对推力器作用时间进行脉宽调制处理。

1 定义坐标系

1)相对轨道坐标系oTxTyTzT:原点oT位于目标航天器质心，xT为地心与目标航天器质心连线背离地心方向，zT为目标航天器轨道面法向，yT与xT，zT形成右手坐标系，如图1所示。

图1 相对轨道系与绕飞参考系示意图

图2 绕飞参考系与期望姿态系示意图

2)绕飞参考坐标系orxryrzr:为便于绕飞轨迹规划与控制而定义，为相对轨道坐标系oTxTyTzT通过方位旋转矩阵RrT转换得到，如图1所示。若绕飞参考系为相对轨道系按3-1-2旋转得到，且旋转角分别为 γrT，αrT和 βrT，则 RrT为

式中，Rx，Ry和Rz分别表示绕x，y和z旋转的主轴旋转矩阵。

3)期望姿态坐标系odxdydzd:为便于描述期望姿态而定义，原点od位于绕飞航天器质心，xd沿绕飞航天器质心与目标质心连线指向目标，yd为绕飞轨道面负法向，zd与xd，yd形成右手系，如图2所示。

2 建立数学模型

绕飞航天器与目标航天器相对位置关系决定其期望姿态指向。首先设计绕飞航天器相对目标的期望相对位置矢量。然后由设计的期望相对位置矢量求取绕飞航天器期望姿态运动规律。最后构建含期望相对位置矢量的相对轨道动力学方程及实际姿态与期望姿态的相对姿态运动学和动力学方程。此方法将航天器快速绕飞监测控制转化为控制实际位置与期望位置误差和实际姿态与期望姿态误差，即实现相对位置跟踪和姿态跟踪控制。

2.1 设计期望相对位置矢量

从航天器空间一般相对运动入手，设计期望相对位置矢量。绕飞参考系内设计期望相对位置矢量lr为

将lr投影到相对轨道系得lT为

式中，RrT为相对轨道系到绕飞参考系的坐标转换矩阵，为常数矩阵，详情见式(1)。

2.2 求取期望姿态运动规律

期望相对运动关系决定绕飞航天器的期望姿态运动规律，体现在期望姿态系的运动规律上。则期望姿态系相对于惯性系的角速度ωdi和角加速度为

式中，ωdr和为期望姿态系相对绕飞参考系的角速度和角加速度;ωrT和为绕飞参考系相对于相对轨道系的角速度和角加速度;ωTi和为相对轨道系相对惯性系的角速度和角加速度;Rdr为绕飞参考系到期望姿态系的坐标转换矩阵。

则绕飞航天器的期望姿态运动规律为

由期望姿态系与绕飞参考系定义，易得Rdr为

式中，符号“‖‖”表示矢量的2范数;由于式中存在相除，必须考虑分母为0的情况。对于Rdr中第1项，当绕飞航天器与目标位置重合时， lr为0;第2项，当绕飞航天器相对目标做直线运动或者静止，l×为0;当第1项或第2项为0，则第3项为

r0。对于Rdr的奇异情况，概括起来属于相对运动稳态情况，此时Rdr为

2.3 相对轨道动力学

为了实现期望相对运动规律、分析相对运动过程和设计相对轨道控制律，需构建包含期望相对位置矢量的相对运动方程，并表示在相对轨道坐标系中，即相对轨道动力学方程。

图3 绕飞航天器与目标航天器相对位置关系示意图

绕飞航天器与目标航天器相对位置关系如图3所示。rt，rs分别表示目标航天器和绕飞航天器在惯性系下位置矢量;Δr是相对位置矢量LT和期望相对位置矢量lT之间的误差矢量。

选择状态量X=［ΔrΔ］T，相对轨道动力学方程写成状态空间形式为

姿态运动学描述姿态角与角速度之间关系。姿态动力学描述航天器在各种力矩作用下绕自身质心的转动。在姿态指向控制中，对绕飞航天器实际姿态进行控制，消除其与期望姿态之间误差，完成姿态指向。

相对姿态运动学方程为

式中，σsd为绕飞航天器本体系相对期望姿态系的姿态MRP表示;M(σsd)的形式参照式(6)中的M(σd);ωsd=ωsi-Rsdωdi为绕飞航天器本体系相对期望姿态系的角速度，ωsi为绕飞航天器本体系相对惯性系的角速度;Rsd为由期望姿态系到绕飞航天器本体系的坐标转换矩阵［8］。

相对姿态动力学方程为

式中，Tcs为姿态控制力矩;Tds为姿态干扰力矩［8］。

3 设计控制律

现有大部分航天器为近圆轨道，忽略摄动后，由线性二次型调节器理论设计最优状态反馈控制律

式中，K=-R-1BTP，而P是代数黎卡提方程式(16)的解，

式中，R为正定对称矩阵;Q为半正定对称矩阵。由uLQR解出作用在航天器本体系上的控制加速度us［7］。

由相对姿态动力学方程，根据Lyapunov稳定性原理设计相对姿态控制律为

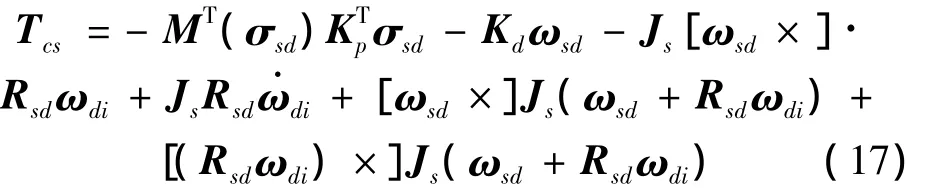
式中，Kd为正定矩阵。稳定性证明参见文献［9-10］。

4 仿真分析

初步设计绕飞航天器推力器(A1-A16)冗余配置方案以及构型主要尺寸如图4所示，推力器参数:推力25N，最小脉冲宽度30ms，比冲2900m/s。引入伪逆法实现控制指令动态分配，并且根据采样周期内作用在航天器上控制冲量和冲量矩相等原则，对推力作用时间进行脉宽调制。

图4 绕飞航天器推力器配置及构型尺寸示意图

若绕飞航天器可达绕飞包络为空间球面或椭球面，则在绕飞参考系内设计期望相对位置矢量为lr=［asinφrcosθrbsinφrsinθrccosφr］T，式中a，b，c为绕飞包络参数，与初始期望相对位置矢量lr0有关;φr∈［0，π］为lr与zr的夹角;θr为lr在xryr平面投影与xr正向的夹角。为使绕飞航天器相对目标航天器的姿态轨道平滑过渡，引入指数函数设计绕飞参数角φr和θr分别为φr=(φr0-φrinf)exp(-1/P1)+φrinf和θr=2π/T·(t+P2exp(-t/P2)-P2)+θr0，式中φr0，θr0为绕飞初始角，由lr0确定;φrinf=π/2;P1，P2为延迟系数，T为绕飞周期。

目标航天器初始轨道参数为:at=42164137m，et=0，it=0°，ut=215°。绕飞航天器初始轨道参数为:as=42164135m，es=0，is=2.71795exp(-6)°，us=214.99932°。绕飞航天器三轴初始姿态角为1°。绕飞航天器质量ms=2000kg，主惯量为 Js=diag(［3256 2922 3505］)kg·m2。假设为球面绕飞取绕飞半径a=b=c=500m;绕飞方位角αrT=70°;绕飞初始角 φr0=20.13°，θr0=269.33°;延迟系数P1=1000s，P2=2000s;绕飞周期T=7200s;仿真时间18000s;采样周期ΔT=0.2s。仿真结果如图5～9。

图5 前7200s相对姿态轨道控制开机时间曲线

图6 前7200s姿态状态跟踪误差曲线

图7 前7200s轨道状态跟踪误差曲线

图8 绕飞航天器在相对轨道坐标系的相对位置曲线

图9 仿真数据可视化验证图

前7200s推力器A1～A16开机时间曲线如图5所示，相对角速度和姿态角跟踪误差曲线如图6所示，相对速度和位置跟踪误差曲线如图7所示。仿真时间内相对位置曲线如图8所示，可视化验证如图9所示。从图8和9看出，绕飞航天器相对目标航天器从初始绕飞面夹角αrT=0°平滑过渡到αrT=70°的绕飞面，并形成与目标航天器轨道面夹角为70°的空间圆绕飞。从图6和7看出，姿态角速度稳态最大跟踪误差约0.04(°)/s，姿态角稳态最大跟踪误差约0.63°，相对速度稳态最大跟踪误差约0.026m/s，相对位置稳态最大跟踪误差约0.55m。故可以满足绕飞航天器始终保持敏感轴指向目标航天器。从推力器开机时间看出，在绕飞启动100s后基本是以推力器最小脉冲来维持绕飞，并且估算出在18000s仿真时间里绕飞航天器需速度增量约15.8065m/s，消耗燃料约11.0926kg。也即在小推力下实现航天器短时间内的快速绕飞监测姿轨耦合控制是可行的。

5 结论

从实现航天器空间一般相对运动与姿态指向入手，研究了航天器任意方位快速绕飞监测控制问题。通过合理定义坐标系使问题转化为相对姿态轨道跟踪控制。引入期望相对位置矢量方便了绕飞航天器轨迹规划、姿态指向求取和控制律设计。考虑了绕飞航天器初始位置不在绕飞面的过渡问题，加入指数函数引导相对姿轨平滑过渡。由仿真结果可以看出，该方法能够解决航天器任意方位快速绕飞监测的设计和控制问题。与航天器的自然绕飞相比，快速绕飞带来燃料消耗，但节省大量时间。航天器对特定目标短时间内的快速绕飞监测是未来空间在轨服务的一种任务工作模式。

［1］张治国，李俊峰，宝音贺西.考虑太阳帆板指向的编队卫星相对姿态跟踪控制［J］.宇航学报，2008，29(1):203-204.(ZHANG Zhiguo，LI Junfeng，BAOYIN Hexi.Relative Attitude Pointing Tracking Control of Satellite Formation Flying with Considering the Orientation of Solar Panel［J］.Journal of Astronautics，2008，29(1):203-204.)

［2］王功波，孟云鹤，郑伟，等.快速绕飞卫星空间圆编队设计方法［J］.宇航学报，2010，31(11):2466-2468.(WANG Gongbo，MENG Yunhe，ZHENG Wei，et al.Fast Fly Around Satellite Space Circle Formation Design［J］.Journal of Astronautics，2010，31(11):2466-2468.)

［3］Masutani Y，Matsushita M，Miyazaki F.Fly Around Maneuvers on A Satellite Orbit by Impulsive Thrust Control［C］//Proceedings of the 2001 IEEE International Conference on Robotics＆Autmation，Seoul Korea:2001:421-426.

［4］朱彦伟，杨乐平.航天器快速绕飞任务的六自由度滑膜控制研究［J］.宇航学报，2009，30(4):1483-1485.(ZHU Yanwei，YANG Leping.6-DOF Sliding Mode Control for Fast Spacecraft Circumnavigation Mission［J］.Journal of Astronautics，2009，30(4):1483-1485.)

［5］朱志斌，李果，何英姿，等.基于滚动优化和微分Theta-D方法的快速绕飞航天器姿轨协同控制［J］.宇航学报，2012，33(2):168-171.(ZHU Zhibin，LI Guo，HE YingZi，et al.Cooperative Relative Attitude and Translation Control Based on Finite Horizon Optimization and Differential Theta-D Method［J］.Journal of Astronautics，2012，33(2):168-171.)

［6］Guang Q Xing，Shabbor A.Design and Implementation of Synchronized Autonomous Orbit and Attitude Control for Multiple Spacecraft Formation Using GPS Measurement Feedback［J］.Frontier Science，2008，2(6):65-70.

［7］Guang Q Xing，Shabbor A.Implementation of Autonomous GPS Guidance and Control for the Spacecraft Formation Flying［J］.Frontier Science，2008，2(5):59-62.

［8］Guang Q Xing，Shabbor A.Alternate Forms of Relative Attitude Kinematics and Dynamics Equations［J］.Frontier Science，2008，2(8):53-59.

［9］Guang Q.Xing，Shabbor A.Parvez.Nonlinear Attitude State Tracking Control for Spacecraft［J］.Journal of Guidance，Control，and Dynaics，2001，24(3):624-625.

［10］Guang Q.Xing，Shabbor A.Relative Attitude Kinematics＆Dynamics Equations and Its Applications to the General Spacecraft Attitude State Tracking Control Problem［J］.Frontier Science，2008，2(7):26-34.

［11］陈寅昕.过驱动航天器推力器动态分配方法［D］.哈尔滨:哈尔滨工业大学，2010，7.

The Relative Coupling Attitude and Orbit Control of Fast Fly-around with Monitoring Spacecraft

ZHANG Qingzhan1，2JIN Yongqiang1，2KANG Zhiyu1，2XIAO Yuzhi1，2
1.Aerospace Transport and Space Service Research and Development Center of SAST，Shanghai 201109，China
2.Aerospace System Engineering Shanghai，Shanghai 201109，China

The relative coupling attitude and orbit control on fast fly-around with monitoring from any orientation in space is researched．By defining fly-around reference and desired attitude coordinate system，the problem is transformed to relative attitude and orbit tracking．Through desired relative position vector designed and desired attitude motion law calculated，the universal model of general relative motion with monitoring is established．And the corresponding control law is supplied．By taking non-coplanar circular flyaround in simulation，with considering fly-around spacecraft not in fly-around plane，the desired relative position vector is designed and the index function is added to smooth relative attitude-orbit．With considering coupling，control commands are distributed dynamically by pseudo-inverse algorithm with redundant thruster deployment．Through the presentation of numerical simulation and visualization，the effectiveness is validated．

book=54,ebook=75

Spacecraft;Fast fly-around;Monitoring;Relative coupling attitude and orbit;Desired relative position vector

V448.22

A

1006-3242(2014)02-0053-07

*上海市科学技术委员会资助课题(13QB1404000)

2013-02-06

张庆展(1987-)，男，山东人，硕士，助理工程师，主要从事航天器相对姿轨耦合控制研究;靳永强(1981-)，男，山西人，博士，高级工程师，主要从事航天器总体GNC领域研究;康志宇(1976-)，男，河北人，博士，研究员，主要从事航天器总体设计研究;肖余之(1964-)，男，江苏人，硕士，研究员，主要从事航天器总体设计研究。