约束最大高度和再入倾角的耗尽关机闭路制导

张志健 王小虎

北京控制与电子技术研究所，北京 100038

约束最大高度和再入倾角的耗尽关机闭路制导

张志健 王小虎

北京控制与电子技术研究所，北京 100038

针对固体助推滑翔弹主动段制导问题，提出一种满足最大高度、再入倾角约束的耗尽关机闭路制导方法。该方法基于开普勒定理和能量守恒定理，得到了满足最大高度、再入倾角约束的自由轨道，并据射程、射向修正轨道，获得导弹需用速度;然后以改进通用能量管理(GEM)方法对发动机剩余能量进行管理，实现了耗尽关机闭路制导。在地球旋转椭球模型下，分别对定轨精度和主动段制导效果进行了数学仿真验证，结果表明:1)修正轨道后，高度、再入倾角精度明显提升，其中倾角误差减小了2个数量级;2)可以高精度地实现不同高度、倾角约束弹道，制导指令姿态变化平缓，有利于控制实现。

闭路制导;耗尽关机;多约束;助推滑翔

远程助推滑翔弹可在临近空间长距离无动力滑翔，具有很强的机动能力、突防能力、隐身性，被各国广泛研究。作为一类新型飞行器，滑翔段射程优化、能量管理和突防轨迹等被大量研究，而与之相适宜的助推段制导控制研究却较少。相对于滑翔段，助推至再入段速度较小、弹道易被预测，随着激光拦截技术、空射主动段拦截弹研究［1］的进步，以及隐身无人机、空天飞机等载体的实际应用，使导弹面临严峻的主动段拦截问题。因此进攻方急需研究适合助推滑翔导弹、强突防、满足多约束条件的新型主动段制导方法。

助推滑翔弹为提高武器生存率、作战效率，采用固体火箭、机动部署、即停即射方案，因此发射点、目标点的相对位置不确定。为攻击不同位置目标，制导系统应根据目标点在线规划弹道，管理多余能量以满足低弹道、再入倾角约束。目前研究中，朱建文［2］在传统调姿能量管理(AEM)［3］基础上，考虑空气阻力影响，得到了低弹道条件耗尽关机方法，但该方法是开环能量管理，易受干扰;许衡、刘鲁华等针对大气层外飞行器，提出样条式能量管理(SEM)［4-5］，得到满足关机点速度大小、速度方向、零攻角约束的耗尽关机方法，但是该方法没有考虑空气阻力，且不具备高度约束;李新国［6］针对助推滑翔弹耗尽关机的特点，通过Newton算法离线优化具有高度和速度约束的飞行程序角，但飞行中使用事先优化的程序角，制导方式易受各种偏差干扰，精度不高。

针对上述不足，本文提出一种满足高度、倾角约束的耗尽关机闭路制导方法。该方法首先利用开普勒轨道和能量守恒得到满足最大高度、再入倾角约束的弹道，并据射向、射程加以修正，以此获得关机需要速度;然后通过管理发动机多余能量实现耗尽关机闭路制导。该方法可实现不同最大高度、再入倾角的自由段轨道，为助推滑翔类飞行器提供良好初始条件，具有结构简单、精度高和姿态角变化平缓的特点。

1 高度、再入倾角约束闭路制导

助推滑翔弹关机后至再入前只受重力影响，其运动学规律符合两体假设，若关机速度满足一定条件，弹道便可满足最大高度、再入倾角约束。求解该速度是闭路制导重要内容。本文方法运用了椭圆轨道和能量守恒定律，得到了简洁的、满足约束条件的解析解弹道;经过高度修正，提高了弹道的精度。该方法原理清晰、计算简单。

1.1 多约束闭路制导原理

假设地球为理想球体，且忽略关机后自由飞行段的气动力影响，则自由段为开普勒椭圆，满足能量守恒。

假设当前高度Hp，再入高度He，再入倾角θe，最大高度Hm已知，且满足同一椭圆轨道。因最大高度出现在轨道远地点，于是以远地点作参考的开普勒椭圆轨道为:

其中，地球引力系数为fM=3．98600×1014;ξ为轨道上点与地心连线和远地点长半轴间的夹角，θ*为当地速度倾角，R*为至地心的距离，V*为相应速度，下标“* ”可取p，m，e，分别代表当前、最高点和再入点，且θe=0。

图1 开普勒轨道

根据能量守恒，再入点和最高点满足:

1.2 轨道修正及需用速度求取

由式(3)可见，计算轨道参数需要最高点和再入点的地心距离。已知条件是弹道最高点、再入点的地理高度。而真实地球为椭球，赤道和南北极地球半径相差21km，故发射点、射向和射程的变化，将改变纬度值，从而影响地心距大小。为更精确地控制最高点和再入点的高度，必须根据弹道参数修正地心距。根据地球参考模型，φ纬度地心到地表距离可表示为［3］:

其中，地球长半轴aE=6．378137×106，第二偏心率e'2=6．73949677548×10-3。

当导弹自由飞行段射程较大时，最高点尤其是再入点的纬度变化较大，必须依据纬度修正最高点、再入点到地心的距离。如图2所示，设A点纬度为φ0，其到B点方位角为α，地心角为β，则B点纬度可由下式确定:

图2 射向、射程与纬度的关系

考虑到高度修正，可按如下步骤求取修正轨道和需用速度:

1)认为当前位置、最高点、再入点的地球半径相等为R0，将高度约束转换为地心距约束:

2)联系再入倾角θe和式(3)可得轨道参数p，e。由于当前点到最高点和再入点的射程角分别为βm，βe，满足 βm=ξp，βe=ξp+ξe，因此由式(1)中第1式可确定射程角:

3)将式(7)代入式(5)得到最高点、再入点对应的纬度，再经式(4)得到相应纬度的地球半径。从而得到修正后的地心距Rm，Re。再重复步骤1)和2)，可得修正后的轨道参数，设为p，e。

4)由椭圆轨道确定当前需用速度。先由最高点地心距Rm和式(1)第2式可得Vm，再据能量守恒式(2)和椭圆方程式(3)可得需用速度大小和倾角:

此Vp，θp即闭路制导期望值，可在每个制导周期计算，当导弹关机时刻达到该值，则自由段可满足最大高度和再入倾角约束。下面介绍如何使导弹在耗尽关机时达到制导期望。

2 耗尽关机能量管理

耗尽关机能量管理的目的是在发动机剩余工作时间内将速度矢量控制到期望值。由于在此过程中，速度和期望速度都在变化，因此能量管理可表示为:

其中，T为发动机推力，R为气动力，g为重力加速度;V0，Vp0为t0时刻速度和期望速度。速度与期望值的偏差为:

注意到，当V0→Vp时，导弹逐渐进入期望轨道，因此有˙Vp→g;又因关机点附近高度已足够大，可忽略空气阻力，因此只要发动机能力足够，必能实现期望速度。下面分析发动机剩余能力。

当燃料一定，发动机总冲固定，能提供的总视速度增量Wa为:

其中，ve为排气速度，m0为点火质量，mco为关机质量，˙m为秒耗量。

在大气层外飞行时，将总视速度增量减去视加速度积分便得到剩余值，而若起始阶段大气阻力不可忽略，则必须考虑空气阻力对视加速度的影响。考虑气动力时，视加速度为:

故由发动机推力产生的视加速度分量为:

因此，t时刻剩余视速度增量为:

其中ts为发动机开机时间。

耗尽关机能量管理制导有很多研究成果［3，5，7-9］，本质是规划Wl的空间路径，使其末端与期望速度矢量重合。已有方法都未同时考虑高度和再入倾角约束，在能量管理阶段会使高度超出限制。因此本文对通用能量管理(GEM)［8］加以改进，以适应限高控制，该方法具有闭环、结构简单、精度高的特点。如图3所示，GEM方法本质为:当Wl大于速度偏差ΔV，则以圆弧轨迹管理能量，让弦长等于速度需求。为满足高度控制目的，本文对原有GEM做了相应调整，将圆心置于轨迹上方。

图3 能量管理角度示意

能量管理中各变量满足如下几何关系:

将正弦函数展开成两阶泰勒多项式，可得:

如图3所示，η为偏差速度与水平面夹角，于是能量管理中俯仰角指令为:

GEM方法可在每个制导周期由ΔV和Wl计算指令姿态，因此控制偏差的影响不会积累，且对重力加速度偏差不敏感，制导精度远高于开环方式。相比传统GEM，改进型圆心在上方，故起始时刻推力指向下方，可减小垂直速度，从而避免最大高度超过限定。

3 仿真验证

以Matlab语言对本文所述求取需用速度的步骤和能量管理方法进行数学仿真验证，仿真中考虑地球旋转椭球模型，所使用弹体参数见文献［5］，飞行起点为赤道，射向为正北，再入点高度为80km。下面分2部分考察弹道计算偏差和耗尽关机制导方式的实现。

仿真中，针对A，B两组不同约束弹道作了分析，其中A弹道最高点110km，再入倾角4°;B弹道最高点90km，再入倾角3°。

3.1 弹道计算偏差分析

由于地球为旋转椭球，本文求取需用速度的步骤中，在解析解的基础上，依据射程、射向做了一次高度修正，下面对修正前后的精度进行对比。分析中，以本文步骤求解确定赤道上方75km处满足A，B弹道的关机速度，再以龙格库塔法求自由段弹道，时间步长为2ms，结果如表1所示。

表1高度和再入倾角约束弹道偏差

A组中，未修正时高度偏差280m，再入倾角偏差0.104°，修正后高度偏差减小为150m，再入倾角偏差0.003°，高度偏差约减小一半，倾角偏差降低2个数量级。B组中，未修正时，高度偏差60m，倾角偏差0.053°，修正后偏差减小为50m，0.001°。可见采用高度修正后，轨道精度有明显提升，尤其是再入倾角偏差，提高了2个数量级。

3.2 耗尽关机制导分析

为验证本文所提耗尽关机闭路制导方法的有效性，针对A，B两种弹道，进行数学仿真。起点在赤道，高度55km，射向正北。为保证制导指令的可实现性，最大姿态角速度限制为10(°)/s。仿真结果如图4～6所示。

由图4可知，A，B弹道都是以负俯仰角飞行，导致y方向速度迅速减小，见图5。相对于A弹道，B弹道的姿态角更小，这是因为B弹道最高点只有90km，需将垂直速度很快减下来。在关机点附近，发动机推力大小会快速变化，不利于姿态控制，所以制导设计中需将关机附近设计为小机动或无机动飞行。由图4可知，本方法中A，B弹道姿态角此时基本为常值，有利于控制实现。图6给出了耗尽关机制导下，导弹从助推至再入的射程、高程轨迹。其中A弹道高度偏差110m，倾角偏差0.03°;B弹道高度偏差70m，倾角偏差0.03°。可见其具有较高的制导精度。注意到该误差与轨道计算偏差不一致，这是由于以下2方面原因:1)制导指令中限制了姿态角速度;2)导弹实际的关机高度与轨道计算偏差分析时设定的75km不一致。

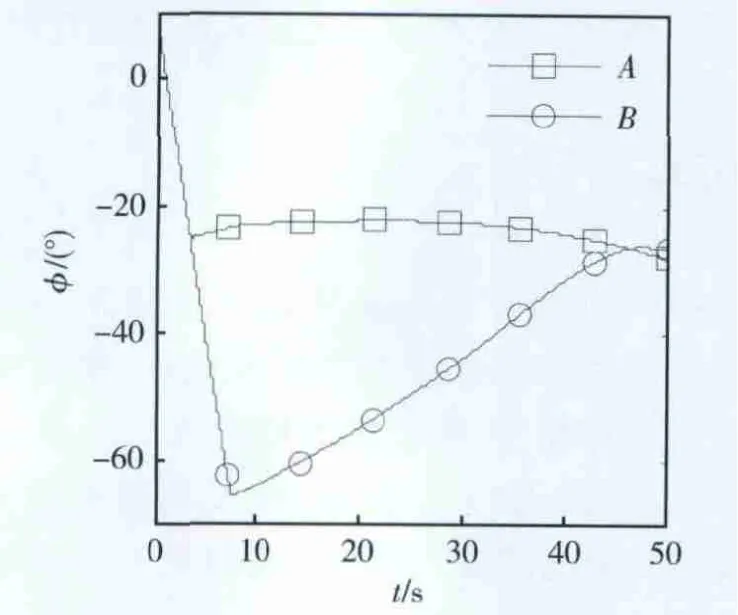
图4 助推段姿态角变化曲线

图5 助推段速度变化轨迹

图6 射程与高度变化轨迹

4 结论

为实现助推滑翔弹耗尽关机条件下最大高度和再入倾角约束，本文提出一种新型耗尽关机闭路制导方法，利用开普勒定理和能量守恒确定弹道，并据射程、射向加以修正，由此得到需要速度;然后利用GEM方法管理发动机多余能量，实现了满足高度、再入倾角约束的耗尽关机闭路制导。该方法可实现不同高度、倾角约束弹道，具有精度高、结构简单、姿态角变化平缓，易于实现的特点。

［1］Zarchan P.Kill Vehicle Guidance and Control Sizing for Boost-phase Intercept［J］.Journal of Guidance Control and Dynamics，2011，34(2):513-521.

［2］朱建文，刘鲁华，汤国建，等.低弹道多约束固体火箭能量管理方法研究［J］.弹箭与制导学报，2012，32(5):121-123.(ZHU Jianwen，LIU Luhua，TANG Guojian，XU Mingliang.Research on Energy Management of Solid Rocket with Multi-constraints and Lower Trajectory［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2012，32(5):121-123.)

［3］陈世年，李连仲，王京武.控制系统设计［M］.北京 :中国宇航出版社，1996:216-229.

［4］Liu Luhua，Chen Kejun，Tang Guojian.Research of Multirestriction Energy Management of Solid Rocket［C］//5th International Conference on Recent Advances in Space Technologies，Ístanbul，TÜRKÍYE ，2011.

［5］Xu Heng，Chen Wanchun.An Energy Management AscentGuidance Algorithm forSolid Rocket-Powered Launch［C］//17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference，San Francisco，USA，2011.

［6］李新国，王晨曦，王文虎.基于修正Newton法的固体火箭能量管理弹道设计［J］.固体火箭技术，2013，36(1):1-5.(LI Xinguo，WANG Chenxi，WANG Wenhu.Energy Management Trajectory Design of Solid Launch Vehicle Based on Modified Newton Method［J］.Journal of Solid Rocket Technology，2013，36(1):1-5.)

［7］周军，潘彦鹏，呼卫军.固体火箭的鲁棒自适应耗尽关机制导方法研究［J］.航天控制，2013，31(3):34-39.(ZHOU Jun，PAN Yanpeng，HU Weijun.A Robust and Adaptive Depleted Shutdown Guidance Method of Solid Rocket［J］.Aerospace Control，2013，31(3):34-39.)

［8］Zarchan P.Tactical and Strategic Missile Guidance［M］.Fifth ed.AIAA Inc，2007:281-289.

［9］姚党鼐，张力，王振国.姿态角单次调整的固体运载火箭耗尽关机能量管理方法［J］.国防科技大学学报，2013，35(1):39-42.(YAO Dangnai， ZHANG Li，WANG Zhenguo.Depleted Shutdown Energy Management Approach for Solid Launch Vehicle with Singular Attitude Angle Adjustment［J］，Journal of National University of Defense Technology，2013，35(1):39-42.)

Depleted Shutdown Closed Loop Guidance with Maximum Height and Reentry Angle Constraint

ZHANG Zhijian WANG Xiaohu
Beijing Institute of Control＆ Electronics Technology，Beijing 100038，China

According to satisfy the constraints of maximum height and reentry angle of boost glide missile，a depleted shutdown closed loop guidance is proposed．The required velocity to meet the constraints is obtained from the ballistic segment trajectory，which is based on theKepler'slaw and the law of conservation of energy and is modified according to its direction and range．And then，the closed loop depleted shutdown guidance is completed by using general energy management(GEM)method to waste excessive energy．Finally，based on the ellipsoid earth model，the precision and effect of proposed method is verified by computer simulation．The results show that the precision of maximum height and reentry angle are improved through modification and particularly the error of reentry angle is decreased by two orders of magnitude．Moreover，the high-precision trajectory of difference height and reentry angle can be achieved and is suitable to control system as the attitude angle command changes slowly．

Closed loop guidance;Depleted shutdown;Multi-constraints;Boost glide

V448.23

A

1006-3242(2014)02-0068-05

2013-08-22

张志健(1986-)，男，湖南人，博士研究生，主要研究方向为导航制导与控制;王小虎(1962-)，男，江苏人，研究员，博士生导师，主要研究方向为精确制导与控制。