供应链库存的模糊机会约束规划模型

李成严，林英丽，赵绍航

1.哈尔滨工业大学计算机科学与技术学院，哈尔滨 150001

2.哈尔滨理工大学计算机科学与技术学院，哈尔滨 150080

供应链库存的模糊机会约束规划模型

李成严1，2，林英丽2，赵绍航2

1.哈尔滨工业大学计算机科学与技术学院，哈尔滨 150001

2.哈尔滨理工大学计算机科学与技术学院，哈尔滨 150080

研究了不确定环境下的供应链库存优化问题。考虑需求为模糊量，且可能在一定条件下不满足约束条件的决策前提，用三角模糊数表示需求，结合可能性理论中的可信性测度，建立了多品种联合补充的模糊机会约束规划模型，目标函数为最小化供应链订货成本和库存成本的期望值。用遗传算法对优化模型求解，以目标函数值作为染色体适应度，给出了编码方案及选择、交叉、变异算子。用数值实例进行了仿真计算，证明了模型和算法的有效性和性能，并给出了不同置信水平下的计算结果。

供应链管理；联合补充问题；模糊机会约束规划；三角模糊数；遗传算法

1 引言

经济全球化带来的竞争压力使各企业不断提高供应链库存管理水平以降低运行成本。多个供应商之间的多品种联合补充问题（Joint Replenishment Problem，JRP）就是在多品种库存补充过程中确定每种产品的订货批量大小及订货周期，从而在满足需求的前提下最小化单位时间内的总成本。研究表明，联合补充可以有效地降低供应链库存成本[1]。

针对实际供应链库存中普遍存在的不确定性，文献[2]将具有随机需求和资源约束的JRP问题用差分进化算法进行求解；文献[3]运用模糊规划求解了模糊需求下的联合补充问题，由已知模糊集的隶属函数求出相应的模糊目标函数的隶属函数，将其转化为是目标函数并求解。但是，模糊规划模型对约束条件只是做了模糊处理，却缺少对模糊事件发生的可能程度的度量。

模糊机会约束规划模型用于描述模糊事件发生的可能程度。其基本思想是允许所做的决策在某种程度上不满足约束条件，但是模糊约束条件成立的可能性不小于决策者预先给定的置信水平[4]；文献[5]又进一步提出可信性测度，具有自对偶特性，在某些方面优于可能性测度。目前，模糊机会约束规划已应用于库存控制[6-7]、产品组合[8]、电力[9]、金融[10]、物流[11]等工程领域。

遗传算法以其擅长全局搜索，具有高度鲁棒性，避免在最优解附近徘徊等优势，在解决JRP的问题中得到了广泛的应用[12]。文献[13]结果表明遗传算法求解过程中效率较高。文献[14]表明遗传算法在寻优能力，稳定性和运算速度上优于克隆选择算法和粒子群算法。

本文采用模糊机会约束规划来讨论不确定环境下供应链库存问题。用三角模糊数表示模糊需求，针对多品种的独立库存优化问题进行分析，建立模糊机会约束规划模型，并用遗传算法进行求解，目标是最小化库存总成本并确定订货周期。

2 用模糊机会约束规划模型求解JRP问题

2.1 联合补充问题的数学模型

联合补充模型主要假设如下：

产品的总资源不确定；

年需求为模糊数，用三角模糊数来表示；

库存补充时间为基本补充周期的整数倍数；

模型不考虑缺货损失。

主要符号如下：

ki为每种产品相对于基本补充周期的倍数；

si为产品i在每个基本补充周期的次要准备成本；

hi为单位库存持有成本系数；

bi为第i中产品的单价；

S为每个基本补充周期的主要准备成本；

n为联合订购的品种数；

T为基本补充周期；

B为资金确定值。

将每种产品的需求看作模糊量Di，在实际决策中，Di的可能范围为[a-d，a+d]，d为一弹性因子，表示不确定的波动范围，而[a，b]为Di的最可能范围值。采用模糊集的思想，将这种不确定需求用三角模糊数来表示，式（1）为年需求的模糊隶属度函数：

其对应的函数图形为如图1所示。

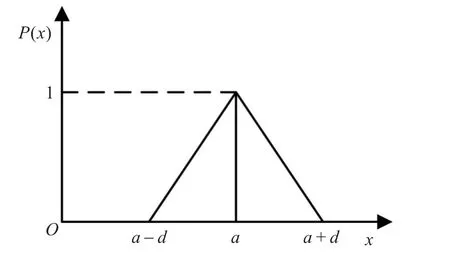
图1 年需求模糊隶属度函数

结合文献[3]中的确定性联合补充模型如公式（2）（3）所示，式（4）为模糊资源约束，表示在单位时间内订货不超过资金上限，式（1）至（5）构成了模糊需求的联合补充问题模型，依据该模型再根据文献[5]和文献[15]，设表示模糊需求下的库存成本，将目标函数当成机会约束对待，模糊目标函数，可推导出本文所需的基于可行性测度的模糊机会约束模型如下：

因此总成本可表示成：

2.2 遗传算法求解模糊机会约束规划模型

遗传学是生物学的重要分支，主要研究基因进化以及其带来的影响。遗传算法将生物进化理论与最优化技术和计算机技术有机结合在一起，遗传算法以其自身优势在解决JRP问题中得到广泛的应用。因此本文采用遗传算法对模糊机会约束规划模型进行求解，基本补充周期长度T和产品相对于基本补充周期的倍数ki是需要确定的决策变量，根据文献[12]设计如下步骤：

（1）编码。根据有意义的最小字符集编码规则和积木块编码规则，将决策变量n用整数表示，编码的长度为n，也就是对n个周期乘子(k1，k2，…，kn)进行整数编码，其中n为联合补充物料的种类。对于策变量T可由公式（8）计算得出。由于在一个基本补充周期内每种产品至少补充1次，所以不比计算ki的下限kiLB，其值为1；而上界k是要满足条件(k+1)，其中要求由于ki不会受交叉和变异的影响，只是在可行域内取值，因此可以取n个随机整数来进行编码。

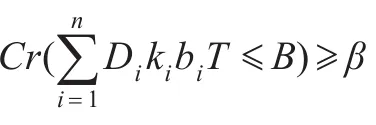
（3）生成初始群体。定义pop_size为染色体个数，并随机产生pop_size个初始的染色体作为初始群体。

（4）适应值函数。适应值函数是基于目标函数来确定并区分群体中个体好坏的标准，是选择操作的依据。本文目标函数TC为最小化总成本，则每个染色体的适应值函数为：

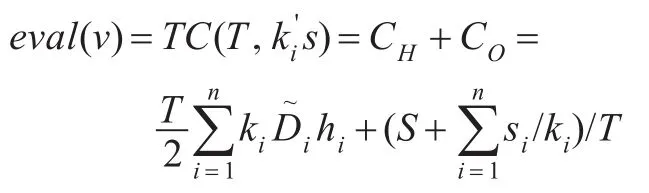
（5）选择。采用赌轮方法选择算子，每个个体进入下一代的概率依据适应度值与整个种群中个体适应度值总和的比例。个体适应值越高，被选中的可能性则越大。

（6）交叉。交叉操作是遗传的核心，采用由二进制编码演变的单点交叉。其操作过程是随机选取断点，然后选取第二个、第一个双亲的断点后部分作为后代的一部分，再从第一个、第二个双亲中按顺序选取合法基因填充余下部分，即要保证每个[1，n]之间的自然数在染色体中只出现m次，这样可避免产生非法个体。例如：

随机选择交叉位置5（由随机数产生）：

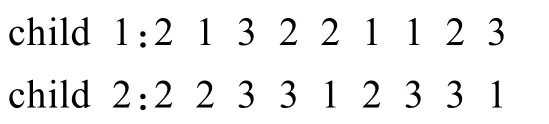
（7）变异。变异操作是生物进化的总要组成部分采用单点变异法。从步骤（5）、（6）所生成的交配池中，按变异概率选择个体，随机产生一个变异的基因位，对该位置的基因进行变异，新基因的范围为1≤Gene(i)≤k。

（8）终止循环条件。以预先设定的最大进化代数Nmax作为停止循环条件。

3 数值实例

本文用VC++实现所提出的模型，当需求Di为三角模糊数时，设a=Di，弹性因子d=0.1Di，各种产品的需求率Di最可能值为在[a-d，a+d]范围内。采用文献[3]中数值实例，如表1所示，设某企业对六种产品进行联合补充，其中主要成本S=$200，每个补充周期可用资金上限B=$25 000，目标为确定决策变量并使总成本值最小。

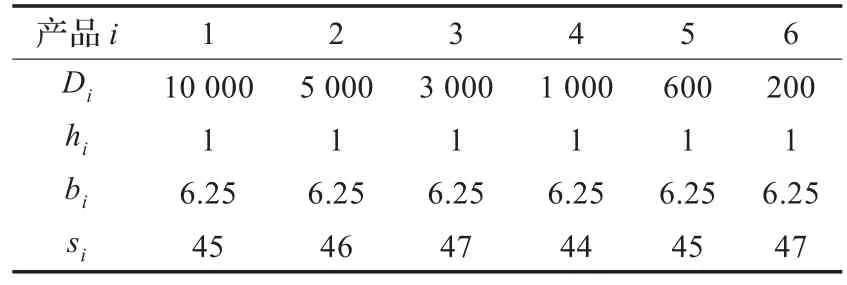
表1 实例数据

遗传算法的参数设置为：种群大小为POPSIZE=30，变异概率为Pm=0.2，交叉概率为Pc=0.3，迭代次数为100次。当置信水平α=0.9，β=0.9时，得到的结果如表2所示。

表2 计算结果

求解过程中，达到最好解的平均迭代次数为8，算法的效率是比较高的。表2中的结果表示基本补充周期的长度为0.168 4，对应的产品1～6的补充周期分别为基本补充周期的1，1，1，2，2，4倍，最优总成本为$4 341.845 0，大于文献[3]实验结果的最优总成本$4 331.003 1，这是由于不确定因素越来越多导致的。为了得到更多数据，当α在[0.5，0.9]区间取值，β=0.9时，得到的结果如表3所示。

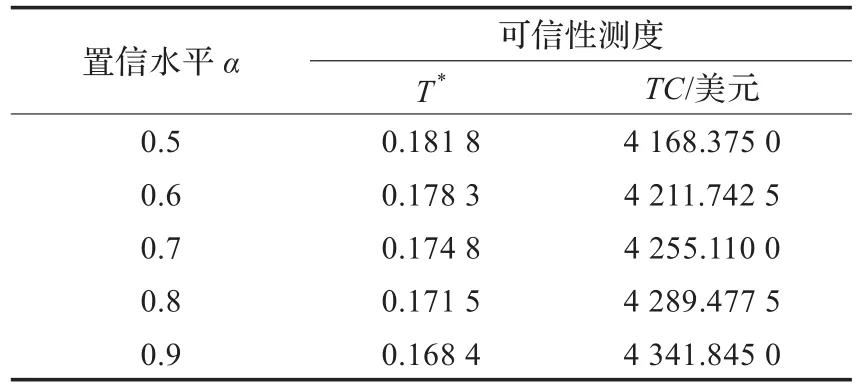
表3 不同置信水平计算结果比较

由表3的结果可知，置信水平α在[0.5，0.9]区间的值越大，联合补充库存成本越高，证明了算法的有效性。

4 结束语

本文主要针对联合补充问题中每种产品需求率进行研究，结合实际应用，利用模糊机会约束规划的思想，用模糊变量表示每种产品的需求率，建立了联合补充问题的模糊机会约束规划模型，利用遗传算法对模型进行求解，并采用数值实例证明了模型和算法的有效性。实现了企业决策者可以通过主观经验判断而非客观概率来确定模糊需求的联合补充问题，本文资源约束的可信性以及对目标函数机会约束处理后的可信性达到决策者设定值时，得到的补充周期和库存总成本，即为基于模糊机会约束规划模型的联合补充问题。所得结果可以为实际应用提供依据。

[1]Moon I K，Cha B C.The joint replenishment and freight consolidation of a warehouse in a supply chain[J].Production Econom ics，2011，133（1）：344-350.

[2]王林，陈璨，曾宇容.资源约束情况下随机性联合采购模型的差分进化算法[J].计算机集成制造系统，2011，17（7）：1541-1546.

[3]包美玲，李成严.模糊需求的联合补充问题研究[J].计算机应与软件，2010，27（9）：91-93.

[4]Xu J，Yao L，Zhao X.A multi-objective chance-constrained network optimal model with random fuzzy coefficients and its application to logistics distribution center location problem[J].Fuzzy optimization Decision Making，2011，10（1）：255-285.

[5]Liu B，Liu Y K.Expected value of fuzzy variable and fuzzy expected value models[J].IEEE Transactions on Fuzzy Systems，2002，10（4）：445-450.

[6]Chien C L.A fuzzy integrated vendor-buyer inventory policy of deteriorating items under credibility measure[C]// IEEE IEEM，2010：1666-1670.

[7]吴杰康，唐力.基于模糊机会约束规划的水火电力系统多目标随机调度模型[J].中国电机工程学报，2011，31（25）：26-34.

[8]张会娟，张强.基于模糊机会约束规划的最优产量决策[J].运筹与管理，2009，18（6）：89-96.

[9]Zhang Y M，Huang G H，Lin Q G.Integer fuzzy credibility constrained programming for power system management[J].Energy，2012，38（1）：398-405.

[10]Li X，Shou B，Qin Z.An expected regret m inim ization portfolio selection model[J].Europe Journal Operation Research，2012，218（2）：484-492.

[11]Pishvaee M S，Torabi S A，Razm i J.Credibility-based fuzzy mathematical programming model for green logistics design under uncertainty[J].Computer Industrial Engineering，2012，62（2）：624-632.

[12]Liu B，Iwamura K.Chance constrained programming with fuzzy parameters[J].Fuzzy Sets and System，1998，94（2）：227-237.

[13]李成严，徐晓飞，战德臣.模糊资源约束的联合补充问题[J].计算机集成与制造系统，2008，13（2）：113-117.

[14]税文兵，叶怀珍，张诗波.物流配送中心动态选址模型及算法研究[J].计算机应用研究，2010，27（12）：4476-4479.

[15]刘宝碇，赵瑞清，王纲.不确定规划与应用[M].北京：清华大学出版社，2008.

LI Chengyan1，2,LIN Yingli2,ZHAO Shaohang2

1.School of Computer Science and Technology, Harbin Institute of Technology, Harbin 150001, China
2.School of Computer Science and Technology, Harbin University of Science and Technology, Harbin 150080, China

Abstract：Supply chain inventory optimization problem under uncertain environment is concerned. Fuzzy chance constrained programming model for multi-item joint replenishment is thus proposed, which can take into account fuzzy demand quantity, as well as the constrained conditions are not satisfied to a certain degree. Demand quantity is a triangular fuzzy number, combined with the possibility of credibility measure theory. The objective function is to minimize the expected discounted cost of ordering and inventories in the supply chain. Genetic Algorithm（GA）is used to solve the obtained optimalityconditions equations, and the fitness function value of the chromosome is the objective value of fuzzy chance constrained programming model. Chromosome coding, selection, crossover and mutation operations are also studied. The feasibility of the model and the effectiveness of the algorithm are illustrated by simulation numerical examples. Some results under different probability level are presented and discussed.

supply chain management; joint replenishment problem; fuzzy chance constrained programming; triangular fuzzy number; genetic algorithm

LI Chengyan, LIN Yingli, ZHAO Shaohang. Fuzzy chance constrained programming model for supply chain inventory.Computer Engineering and Applications, 2014, 50（17）：241-244.

A

TP399

10.3778/j.issn.1002-8331.1311-0468

哈尔滨市攻关项目（No.2011AA 1CG063）；黑龙江省教育厅资助项目（No.12541142）。

李成严（1972—），男，在读博士，教授，研究领域为企业智能计算；林英丽（1989—），女，硕士研究生；赵绍航（1989—），男，硕士研究生。E-mail：linyinglide@163.com

2013-12-02

2014-03-13

1002-8331（2014）17-0241-04