基于权重参数实时更新的室内定位算法

周雄，陈国彬

重庆工商大学融智学院，重庆 400033

基于权重参数实时更新的室内定位算法

周雄，陈国彬

重庆工商大学融智学院，重庆 400033

为了提高室内节点的定位精度，提出一种基于权值参数实时更新的室内定位算法。选择3个最能反映待定位点信息的访问接入点，实时获取测距模型的参数，并采用最小二乘支持向量机对测距进行补偿，得到距离权重，三边定位算法根据权重对节点进行定位，并对计算中的距离进行加权处理，采用卡尔曼滤波法对定位误差的进行校正。实验结果表明，该算法可以较好地降低环境变化和测量误差对定位的不利影响，提高了室内节点的定位精度。

室内定位；无线网络；最小二乘支持向量机；卡尔曼滤波

1 引言

随着无线通信技术和智能移动终端不断发展，位置服务已经得到迅速普及，无线定位技术在军事、交通、物流、医疗、民生等领域得到了广泛的应用。在室外空旷的环境下，全球定位系统（Global Position System，GPS）通过卫星的授时和测距对用户节点进行定位，具有定位精度高、实时性好、抗干扰能力强等优点[1]。相对于室外环境，室内环境更加复杂，信号传播易受到人员、墙体以及其他障碍物的阻挡，定位难度增加，GPS捕捉卫星信号相当微弱，其定位性能不能满足实际人们生产活动定位精度的需求，因此如何提高室内定位精度已成为当前无线定位技术研究中的热点[2-3]。

针对无线室内定位问题，大量学者和研究人员进行了深入的研究，提出许多有效的室内定位算法[4]。根据定位原理，室内定位算法主要分为两类：时间测距定位和接收信号强度（Received Signal Strength Indication，RSSI）定位[5]。基于时间测距的定位方法主要包括：信号到达时间（Time Of A rrival，TOA）定位、信号到达时间差（Time Difference of A rrival，TDOA）定位等[6-9]。基于TOA定位算法存在对噪声敏感、多路径反射以及参考时钟不精确等缺陷，距离估计误差大；基于TDOA定位算法要求各设备间同步，但由于室内距离有限，导致测得距离误差较大，同时它们在定位过程中需要其他辅助设备的支持，因此在室内定位中，这些算法难以真正有效实现[10]。基于RSSI的定位思想为：首先得到发射节点的发射信号强度，接收节点根据收到信号的强度计算出信号的传播损耗，然后通过传输损耗模型得到待定位点到访问接入点（Access Point，AP）之间的距离，再选择合适的算法计算出节点的位置，从而实现对定位节点的精确定位。相对于时间测试距定位算法，其不需要添加额外的硬件设备，简单易实现，成本低，可以将定位系统的应用范围扩大到楼群和室内，因此成为室内定位的主要研究方向[11]。但是在实际室内环境中，信号传播过程受到传播方向、通信多径现象以及室内结构等环境因素的影响，AP的RSSI值不固定，具有时变性，如果直接采用AP的RSS值为输入，实现室内定位，导致室内定位误差大，精度低。针对该难题，许多学者在RSSI定位算法的基础上，对环境影响因素进行了分析，提出许多学改进的RSSI室内定位算法，对各种不利影响进行抑制，消除估计误差，以提高室内定位的精度[12]。

为了提高室内节点定位的精度，提出一种基于权值参数实时更新（Weight Parameter Real-time Updating，WPRU）的室内定位算法，并通过仿真实验测试本文算法的有效性和优越性。仿真结果表明，WPRU减少因环境因素以及信号强度测量过程的误差，提高了室内定位的精度。

2 三边定位算法

在理想情况下，由测距阶段得到的待定位点到3个AP的距离就可以计算出待定位点的位置，即以已知位置的三个AP为圆心，以其各自到待定位点的距离为半径做圆，所得三个圆的交点，即为待定位点的位置[13]。

如图1所示，设未知节点D坐标为(x，y)，A，B，C三个点坐标分别为(xA，yA)、(xB，yB)、(xC，yC)，它们到点D的距离分别为dA、dB、dC，根据距离公式得到以下方程组：

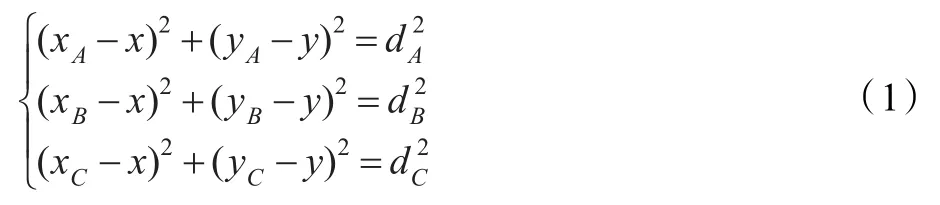
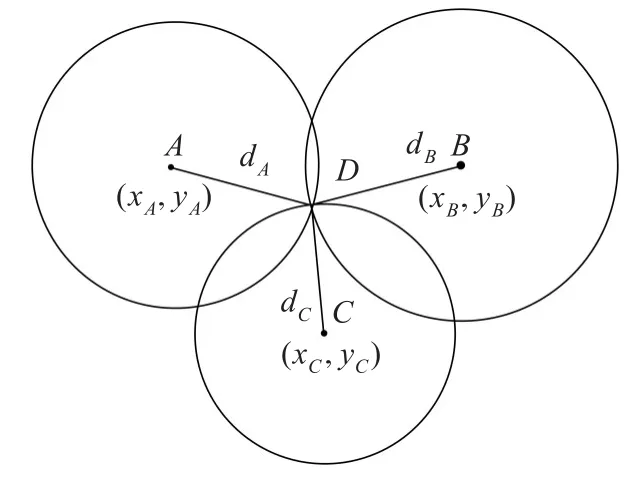
图1 三边定位法示意图

3 WPRU定位算法

3.1 WPRU算法的工作流程

WPRU算法首先实时获取测距模型参数A和n的值，然后采用最小二乘支持向量机补偿测距误差，然后计算距离权重，并采用三边定位算法进行定位，最后采用卡尔曼滤波法对定位误差进行校正，以提高定位精度，具体如图2所示。

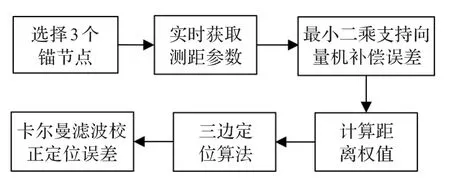
图2 WPRU算法的工作流程

在城市、郊区等环境，接收到的信号强度为：

式中，n为信号路径传播耗散系数；RSSIr为接收到的信号强度；A为在参考距离的接收信号强度。

对式（3）进行推导，可以得：

受到多种因素的影响，如人员走动，A和n值的变化比较大，对于不同室内环境，其值不相同，它们的值根据经验进行设置，有时误差相当大，因此需根据具体定位环境，找到最能反映定位环境的参数值，以提高室内定位的精度。

已知3个锚节点A(xA，yA)，B(xB，yB)，C(xC，yC)的位置，C点的当前环境下A、B两个点信号强度RSSIA、RSSIB，按照测距模型得：

对式（5）进行求解，可以得到A和n的值，这样它们的值可以准确反映当前环境下的实时参数值。

3.2 设置距离的权值

文献[14]指出，随着距离的增大，信号强度的误差相应增大，在实时获取参数A和n的值同时，需要对测距距离进行加权处理，降低信号强度和距离引起的误差。权重参数反映了不同AP对目标点的影响程度，而距离可以反映目标点和AP之间位置关系，因此采用距离平方的倒数作为权值，权重参数ωi计算公式为：

式中，di为目标点到AP距离大小的序列。

目标点的位置计算公式为：

3.3 误差补偿

设实际距离为d，则实际距离d与测量距离d′间存在如下关系：

式中，∆E表示误差。

采用最小二乘支持向量机对误差进行预测和补偿，LSSVM的回归函数为：

式中，ω表示为权向量。

综合考虑函数的复杂度和拟合误差，最小二乘支持向量机的目标函数为：

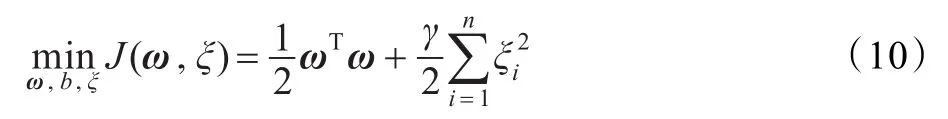
式中，ξi为误差变量；γ为正则化参数。

根据Karush-Kuhn-Tucker（KKT）最优条件，得到如下线性方程组：

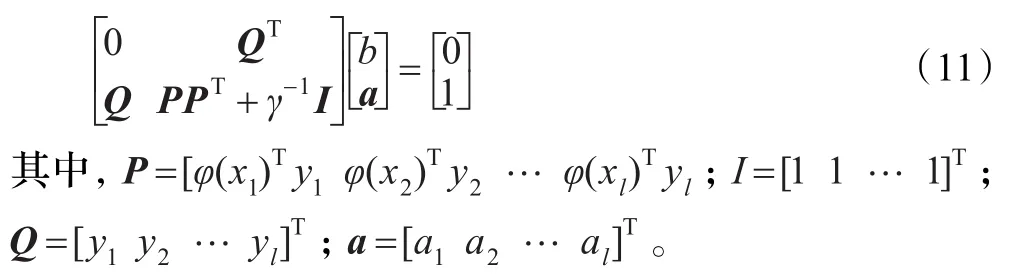
根据Mercer条件，核函数可写为：

计算b，a后，最小二乘支持向量机的回归函数为：

径向基核函数具有参数少，通用性好等优点，选择该函数作为最小二乘支持向量机的核函数，具体定义如下：

通过式（14）建立了距离误差函数，得到相应的预测误差值(∆E′)，并进行误差补偿，即

其中，d″为未知节点与锚节点间的测量距离修正值。

3.4 卡尔曼滤波修正误差

为了得到更准确的信号强度值，使用卡尔曼滤波修正误差，卡尔曼滤波通过线性随机差分方程来评估离散系统过程中状态变量x的一个过程，其表达形式如下：

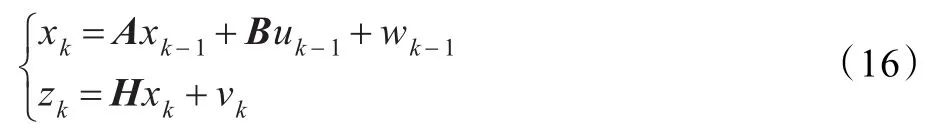
式中，A∈Rn×n为状态转移矩阵；uk-1和B分别为输入变量和与之对应的系数矩阵；zk∈Rm为测量值；H∈Rm×n为测量矩阵；随机变量wk和vk分别表示滤波系统误差和测量误差，它们被假定为相互独立且具有标准正态分布的白噪声，即

式中，Q为滤波过程噪声协方差矩阵，R为测量噪声协方差矩阵[15]。

卡尔曼滤波器的计算方程分为两组：时间更新方程和测量更新方程；时间更新方程中当前阶段的预测状态通过上个阶段的状态和误差协方差矩阵获得；测量更新方程则将当前阶段的测量值与当前阶段的预测状态结合起来获得当前阶段的状态。时间更新方程的数学表达如下：

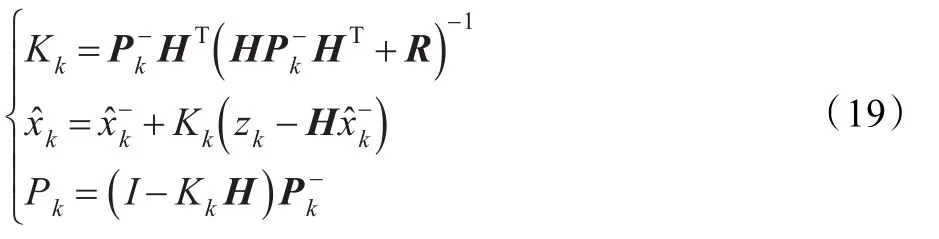
式中，Kk为卡尔曼增益，zk为当前阶段的测量值。

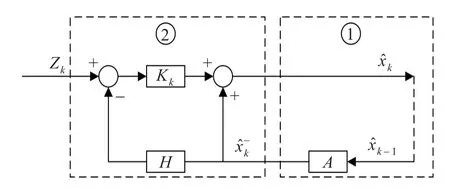
图3 卡尔曼滤波方框图

定位算法的位置用zk表示，先前状态得到的定位位置用表示，整个卡尔曼滤波过程应用在每次误差计算中，对协方差进行不断递归，卡尔曼增益不断调节，并将校正后的距离用在新的定位计算中。

4 仿真实验

4.1 仿真环境

为了测试本文算法的性能，实验场景大小为10 m× 40 m的区域，在4个顶点部署4个锚节点，中间隔放置4个锚节点。定位误差计算公式为：

式中，(x，y)表示计算得到的待定位点的位置；(x′，y′)表示待定位点实际的位置。

4.2 参数实时更新对定位的影响

为了测距模型参数实时更新对定位结果的影响，采用经验参数确定方法进行对比实验，待定位节点在室内进行随机移动，并不断测量AP节点发送来的信号强度信息，它们待定位点的位置如图4所示。

实时获取参数方法和参数经验设置方法的定位误差如图5所示，从图5可知，相对于经验设置参数值方法，实时获取参数方法定位误差明显减小，而且波动范围较小，对比结果表明，由于实时获取参数方法可以较好地描述实验场景动态变化，适用范围更广，定位结果更加可靠。

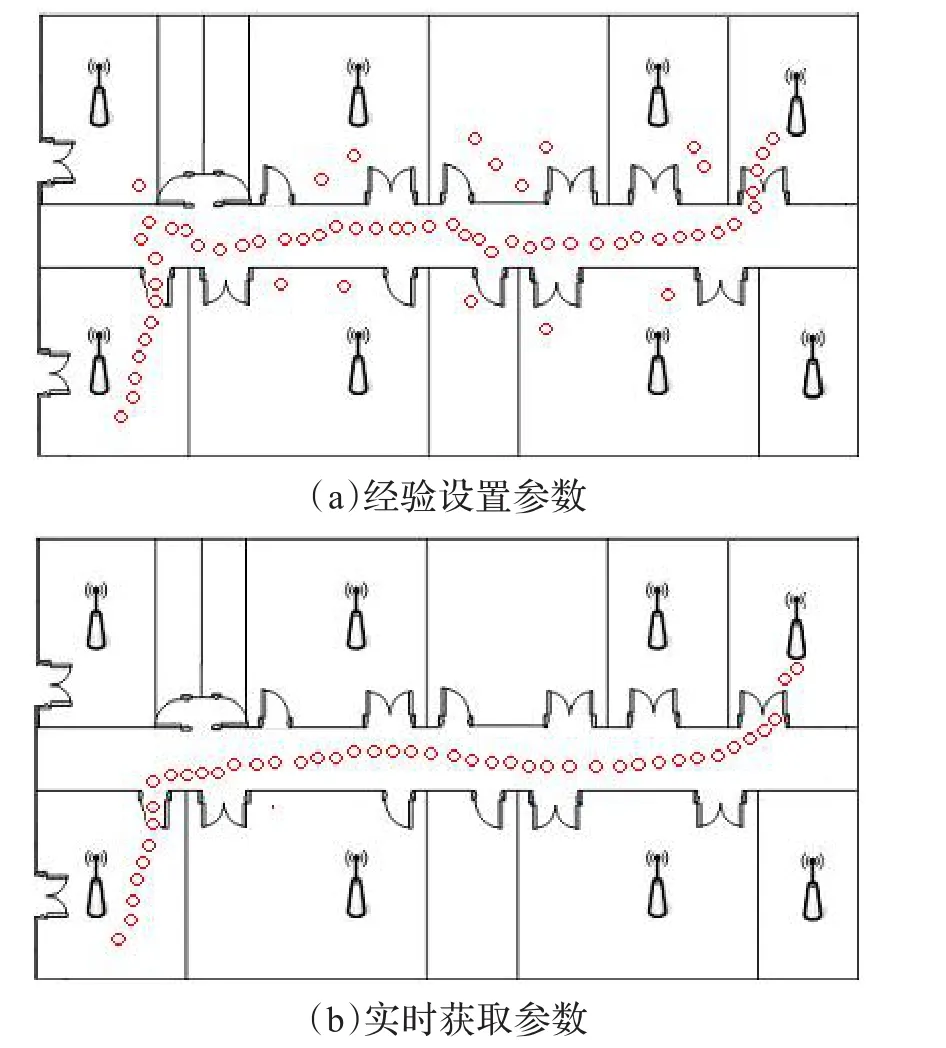
图4 两种方法的节点定位轨迹

图5 实时和经验参数定位方法的误差比较

4.3 卡尔曼滤波对定位结果的影响

为了测试卡尔曼滤波的作用，采用没有卡尔曼滤波定位方法进行对比实验，两种方法的定位误差的变化曲线如图6所示。从图可知，卡尔曼滤波法的平均定位误差较小，50次实验平均定位误差变化平稳，较好解决了RSSI测距误差室内定位的不利影响，而没有采用卡尔曼滤波法的平均定位误差变化比较剧烈，误差较大，定位结果不可靠，对比结果证明了WPRU方法采用卡尔曼滤波法校正定位算法误差的思想是正确的，有利于提高室内的定位精度。

4.4 与其他定位方法的性能对比

为了使WPRU定位算法的结果更具说服力，选择三边定位算法、文献[14]的室内定位算法进行对比实验，它们的结果见表1所示。对表1的结果进行分析，可以得到如下结论：

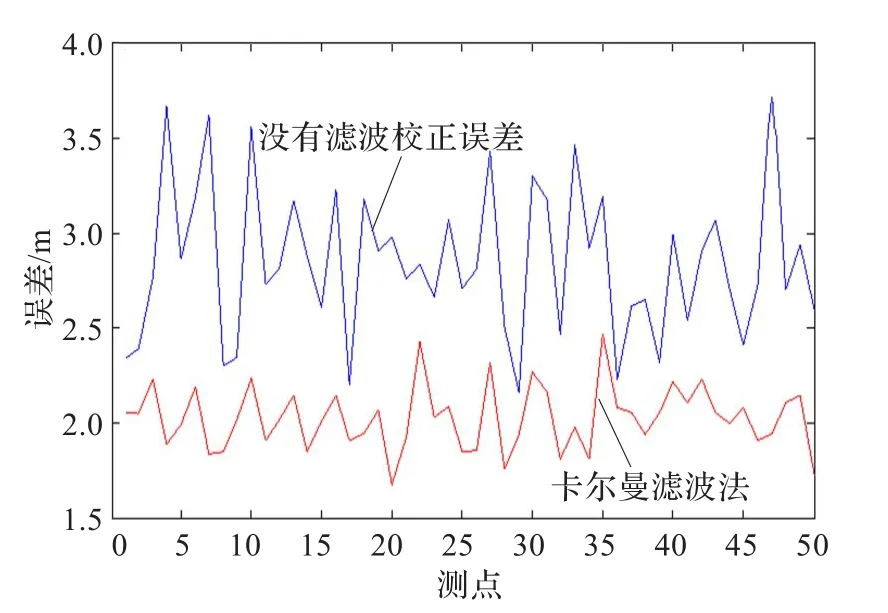
图6 卡尔曼滤波法对定位误差的影响

（1）相对于三边定位算法，WPRU算法的定位精度显著提高，定位误差大变化幅度减小，这是因为在实际定位过程中，由于测距存在着误差，使得三圆心未必会交于一点，使三边定位算法的定位误差较大，而WPRU算法通过实时采集测距模型的参数，减少了测距误差，并通过卡尔曼滤波对定位误差进行校正，有效提高了室内的定位精度。

（2）相对于文献[14]的定位算法，WPRU算法的定位精度得到了相应提高，主要由于WPRU算法采用最小二乘支持向量机对距离误差进行补偿，减少了定位误差，一定程度上可以提高室内的定位精度。

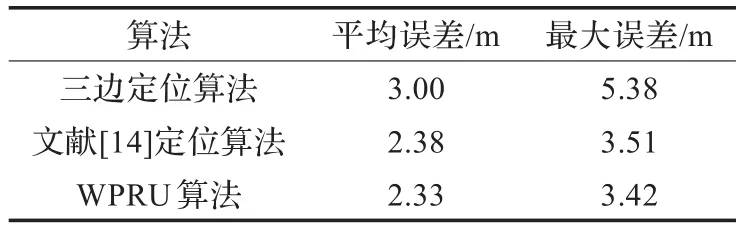
表1 不同定位算法的定位误差比较

WPRU定位算法与其他算法的定位速度进行对比实验，采用定位时间作为衡量指标，它们的结果如图7所示，从图7可知，相对于三边定位算法和文献[14]的定位算法，WPRU定位算法的定位时间更短，定位最快，可以较好地满足无线室内定位的实时性要求。

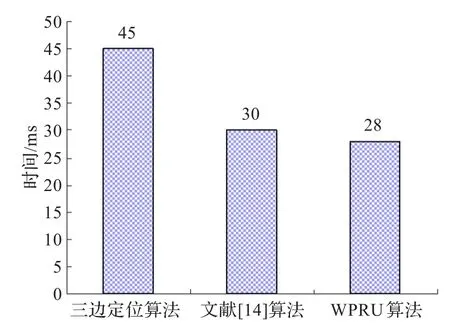
图7 不同算法的定位速度对比

5 结语

针对室内定位精度低的难题，提出一种基于WPRU定位算法，并通过仿真实验测试算法的性能。仿真结果表明，WPRU算法不仅提高了室内定位的精度，降低了定位的误差，同时没有增加定位成本，具有更大的实用值。

[1]Gu Y Y，Lo A，Niemegeers I.A survey of indoor positioning systems for wireless personal networks[J].IEEE Communications Surveys&Tutorials，2009，11（1）：13-32.

[2]Bshara M，Orguner U，Gustafsson F，et al.Fingerprinting localization in wireless networks based on received-signalstrength measurements：a case study on W iMAX networks[J].IEEE Trans on Veh Technol，2010，59（1）：283-294.

[3]Bulusu N，Heidemann J，Estrin D.GPS-less low cost outdoor localization for very small devices[J].IEEE Personal Communications M agazine，2000，7（5）：28-34.

[4]朱剑，赵海，孙佩刚，等.基于RSSI均值的等边三角形定位算法[J].东北大学学报，2007，28（8）：1094-1097.

[5]刘运杰，金明录，崔承毅.基于RSSI的无线传感器网络修正加权定位算法[J].传感技术学报，2009，23（5）：717-721.

[6]徐凤燕，单杭冠，王宗欣.一种带参数估计的基于接收信号强度的室内定位算法[J].微波学报，2008，24（2）：67-72.

[7]张明华，张申生，曹健.无线局域网中基于信号强度的室内定位[J].计算机科学，2007，34（6）：68-71.

[8]刘召伟，徐凤燕，王宗欣.基于参数拟合的室内多用户定位算法[J].电波科学学报，2009，23（6）：1090-1094.

[9]Agustín E，Salcedoz S，Vidales P，et al.Near optimal cityWide W iFi network deployment using a hybrid grouping genetic algorithm[J].Expert Systems with Applications，2011，38（8）：9543-9556.

[10]倪巍，王宗欣.基于接收信号强度测量的室内定位算法[J].复旦学报：自然科学版，2004，43（1）：72-76.

[11]Carlos K F，Inmaculada M J，A licia G C，et al.Nonparametric model comparison and uncertainty evaluation for signal strength indoor location[J].IEEE Transactions on Mobile Computing，2009，8（9）：1250-1264.

[12]万国锋，钟俊.基于三角形理论的无线传感器网络定位算法[J].计算机应用研究，2013，30（1）：249-251.

[13]Kushki A，Plataniotis K，Venetsanopoulos A.Intelligent dynamic radio tracking in indoor wireless local area networks[J].IEEE Transactions on M obile Computing，2010，9（3）：405-419.

[14]白云.一种传播模型无关的快速W iFi访问点定位算法[J].小型微型计算机系统，2013，34（2）：220-223.

[15]Raman Kumar K，Apte V，Powar Y A.Improving the accuracy of wireless LAN based location determ ination systems using Kalman filter and multiple observers[C]//IEEE Wireless Communication and Networking Conference，Las Vegas，USA，2006，1：463-468.

ZHOU Xiong,CHEN Guobin

College of Rongzhi, Chongqing Technology and Business University, Chongqing 400033, China

In order to improve the localization precision, a novel indoor localization algorithm based on weight parameter real-time updating is proposed in this paper. Three APs which can best explain the information of object are selected, and then the parameters of range model are updated in a real-time way, and the least square support vector machine is used to correct the range error to obtain the distance weights, the localization is obtained by using triangle-based localization algorithm based on distance weights and the localization error is corrected by Kalman filter method. The experimental results show that the proposed algorithm can reduce the error caused by surroundings and signal strength, and it has improved the higher localization precision.

indoor location;wireless network;least square support vector machine;Kalman filter

ZHOU Xiong, CHEN Guobin. Indoor localization algorithm based on weight parameter real-time updating. Computer Engineering and Applications, 2014, 50（17）：191-194.

A

TP393

10.3778/j.issn.1002-8331.1401-0396

重庆市教委科学技术研究项目（No.KJ133103）。

周雄（1980—），男，高级工程师，主研领域为计算机网络类；陈国彬（1982—），男，讲师，主研领域为计算机网络类。

2014-01-23

2014-03-10

1002-8331（2014）17-0191-04

CNKI网络优先出版：2014-08-05,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1401-0396.htm l