比例最小偏度单行采样的平方根UKF-SLAM算法

汪贵冬，陈跃东，陈孟元

安徽工程大学安徽省电气传动与控制重点实验室，安徽芜湖 241000

比例最小偏度单行采样的平方根UKF-SLAM算法

汪贵冬，陈跃东，陈孟元

安徽工程大学安徽省电气传动与控制重点实验室，安徽芜湖 241000

对于UKF-SLAM算法所存在的滤波增益矩阵计算失真，采用对称采样计算复杂度相对较高且易产生非局部效应等问题，提出基于比例最小偏度单行采样的平方根UKF-SLAM算法。改进后的算法采用协方差阵的平方根代替协方差阵带入迭代运算，并以比例最小偏度单行采样的方式优化采样策略。仿真结果表明，该算法能够有效地提高机器人位姿以及特征地图的估计精度，并降低了计算复杂度，提高算法的稳定性。

滤波增益；采样策略；平方根；计算复杂度

未知环境下，利用自身所携带的传感器，机器人递增式地创建环境的特征地图，与此同时在创建的地图中修正自身的位置，即移动机器人的同步定位与地图构建问题（Simultaneous Localization and Mapping，SLAM）[1]。应用于SLAM的经典算法是将机器人的运动模型和观测模型进行一阶泰勒级数展开，然后利用扩展卡尔曼滤波（Extended Kalman Filter，EKF）对机器人的位姿以及特征图进行同时最优估计。此模型最早是由Sm ith和Cheeseman提出[2-3]。诸多国内外学者基于EKF-SLAM框架，进行优化与改进。例如，吕太之提出的采用极坐标对比临近两次的观测值来检测与减小外部干扰，提高算法的估计精度与鲁棒性[4]；张海强等提出改进的压缩型EKF-SLAM算法来降低计算复杂度[5]；周武等则提出全局观测地图模型来改进地图的表征方式[6]。但线性化过程中产生的截断误差，且雅克比矩阵计算量大等固有缺陷使得EKF-SLAM算法并不适合在大规模的环境地图中使用[7]。

因此，在研究如何改进EKF-SLAM的同时，Julier等人提出了一种可以直接应用于非线性系统的新型滤波器[8]，即无迹卡尔曼滤波[9]（UKF）。UKF是一种基于最小方差估计准则的非线性高斯状态估计器。类似于扩展卡尔曼滤波，均使用高斯随机变量来近似状态分布，不同的是，UKF使用一些确定性采样得到的加权采样点（Sigma点）来逼近。利用这些采样点，可以较好地描述高斯随机变量真实的均值及方差，其精度逼近泰勒二阶，而同等条件下的EKF只能达到一阶精度。在计算复杂度上，UKF与EKF属于同阶次的，且无需进行雅克比矩阵的计算，所以UKF更易于实现[10]。进一步研究发现，由于计算机的舍入误差，UKF算法的状态协方差阵在传递的过程中，易失去非负定性和对称性，从而造成滤波器的发散。平方根滤波[11]指出传递协方差阵的平方根代替传递协方差阵本身很好地解决了这一问题，并成功应用于GPS/DR组合定位[12]与室内定位[13]中。

本文首先对UKF算法与平方根UKF算法（SR-UKF）应用于SLAM过程进行MATLAB对比仿真实验，得出SR-UKF算法可以明显提高机器人位姿估计的精度。但对于SLAM这种对实时性要求较高的系统，降低计算复杂度、提高计算效率也是至关重要的[14]。再对SR-UKF算法进行深入研究，考虑通过改变采样策略，使用比例最小偏度单行采样代替对称采样，减少Sigma点数目来降低算法的计算复杂度，从而提高实时性。因此，提出一种基于比例最小偏度单行采样的平方根UKF（SPSR-UKF）算法。

1 SLAM问题的概率描述

其中，Z1:k和u1:k为已知条件。采用贝叶斯滤波原理计算式（1）的后验概率分布，获得状态的最优估计。整个过程分为两个步骤，第一步进行预测，由机器人的位姿计算模型以及k-1时刻的后验概率分布得到k时刻的先验概率分布：

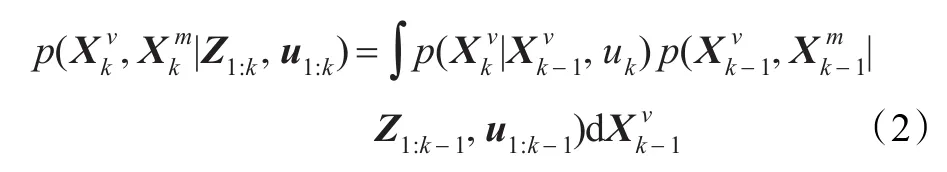
第二步进行观测更新。由系统的观测模型得到k时刻的观测值Zk，实现由先验概率分布求解后验概率分布：

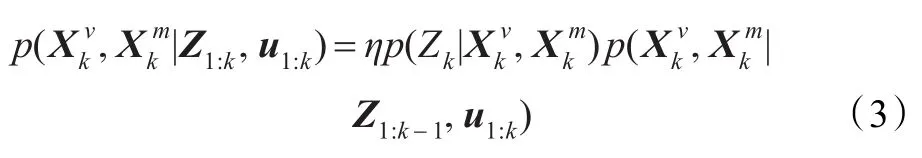
其中，η为归一化系数。

2 SR-UKF-SLAM算法

2.1 UKF-SLAM算法

UKF以UT变换为核心，以卡尔曼滤波为基本框架，使用确定性采样的方式得到状态估计的后验状态分布。在进行滤波之前，将原来的状态向量增广为高斯噪声变量：

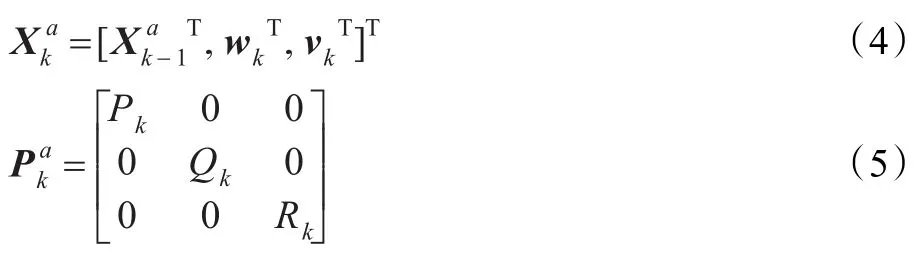
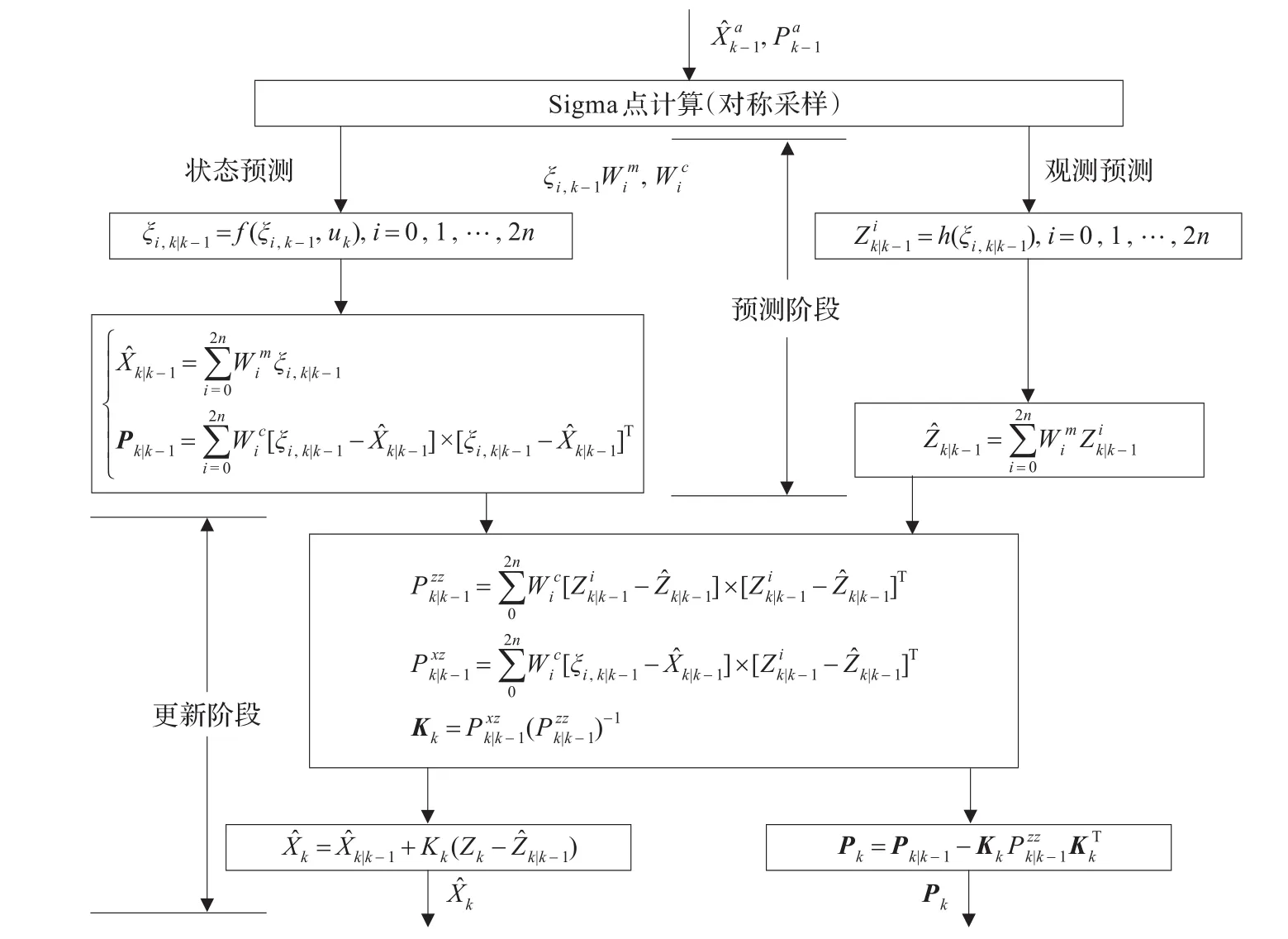
图1 UKF-SLAM算法框图

2.2 SR-UKF-SLAM算法

在上述的滤波模型中，计算机的舍入误差随着滤波的深入逐渐累积，滤波误差协方差矩阵Pk和预测误差协方差阵Pk|k-1失去非负定性和对称性的可能性也随之增大，使得滤波增益Kk计算失真，造成滤波器发散。因此，在UKF-SLAM算法模型的基础上，用协方差平方根Sk更新代替协方差Pk更新(Pk=Sk)，提出基于平方根的UKF-SLAM算法（SR-UKF-SLAM）。具体算法过程中，需要用到QR分解以及Cholesky因子更新两种运算方式来降低计算复杂度。区别于UKF-SLAM算法，其优化过程如下：

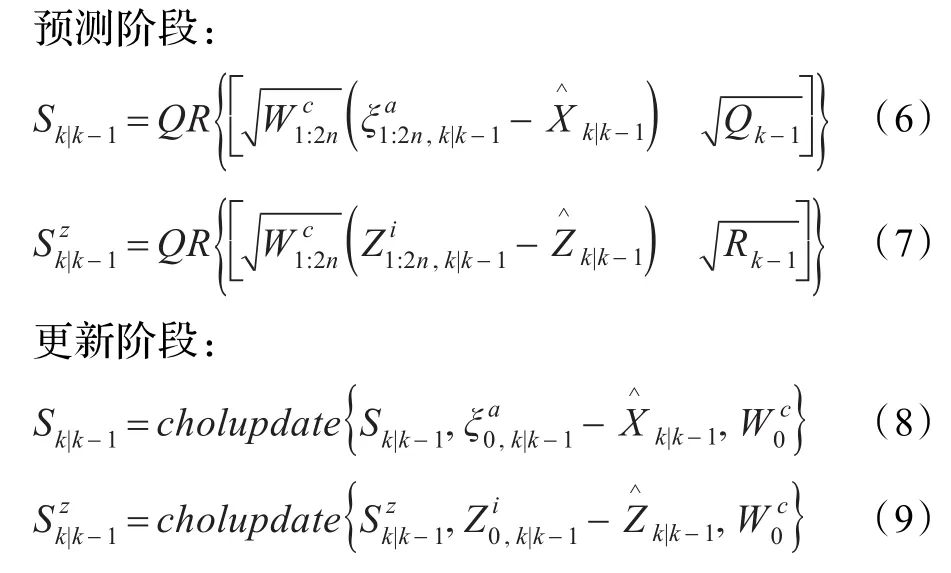
为了避免矩阵逆运算，在对滤波增益Kk的处理上，考虑采用回代法求解，如式（10）所示。最终用式（11）、（13）对状态向量进行迭代更新。

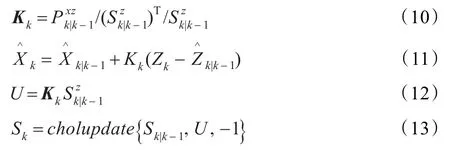
3 SPSR-UKF-SLAM算法

虽然SR-UKF-SLAM算法在一定程度提高了机器人位姿和特征地图的估计精度，但对于SLAM这种对实时性要求较高的系统，希望通过减少Sigma点的数目来进一步降低计算复杂度。且在对称采样中，Sigma点到中心的距离随的状态维数增加而增大，这样易产生非局部效应，影响了滤波的精度与稳定性。

最小偏度单行采样是一种采样点数最少的采样方式，由于采样点个数对UKF的计算量有着直接影响，因此，该策略更适合应用于实时性较高的系统中。根据Julier等人在文献[16]中的分析，对于n维状态分布向量，至少需要n+1个采样点来确定系统的验后分布。研究发现，比例修正可以很好地解决非局部效应的问题。因此，本文结合上述采样策略的优点，应用到SLAM过程中，提出一种基于比例最小偏度的平方根UKF-SLAM算法，即SPSR-UKF-SLAM算法。算法修正了SR-UKF-SLAM算法的采样策略，其具体采样过程如下：

（3）初始向量(L=1)为：

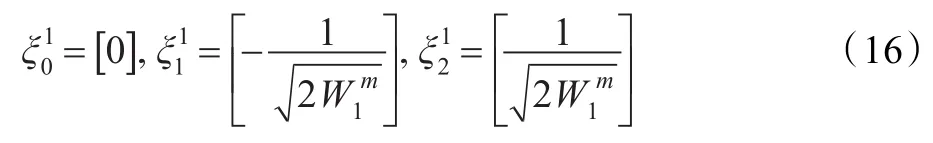
对于输入的状态维数L=2，3，…，n时，向量的迭代公式为：

4 算法仿真实验及其仿真结果分析

为了研究改进后的算法对估计精度的影响，在MATLAB仿真环境下，利用Tim Bailey开发的开源仿真平台，分别对UKF-SLAM、SR-UKF-SLAM以及SPSRUKF-SLAM进行仿真实验。计算机采用Inter Core-i5的双核处理器，主频2.6 GHz，内存为4 GB。在实验中，模拟250 m×200 m的室外环境，机器人从坐标点（0，0）沿17个路径点（“•”）巡游一圈，机器人的行使速度为2 m/s，环境中随机分布了35个静止的特征点（“*”），两种算法的仿真结果如图2～图4所示，细线表示机器人的理想运动轨迹。虚线表示机器人的估计路径，“+”为SLAM估计的特征点位置，椭圆表示特征点估计的误差范围。图2至图4表明，在初始阶段，UKF-SLAM与SRUKF-SLAM计算误差相似，但随着时间的推移，由于新的特征不断加入，UKF-SLAM的机器人估计轨迹偏离理想运动轨迹的程度越来越大，且特征地图的误差椭圆也明显大于SR-UKF-SLAM算法。与SR-UKF-SLAM算法相比，而SPSR-UKF-SLAM算法过程中，机器人估计轨迹进一步逼近理想的运动轨迹，且误差椭圆进一步缩小。

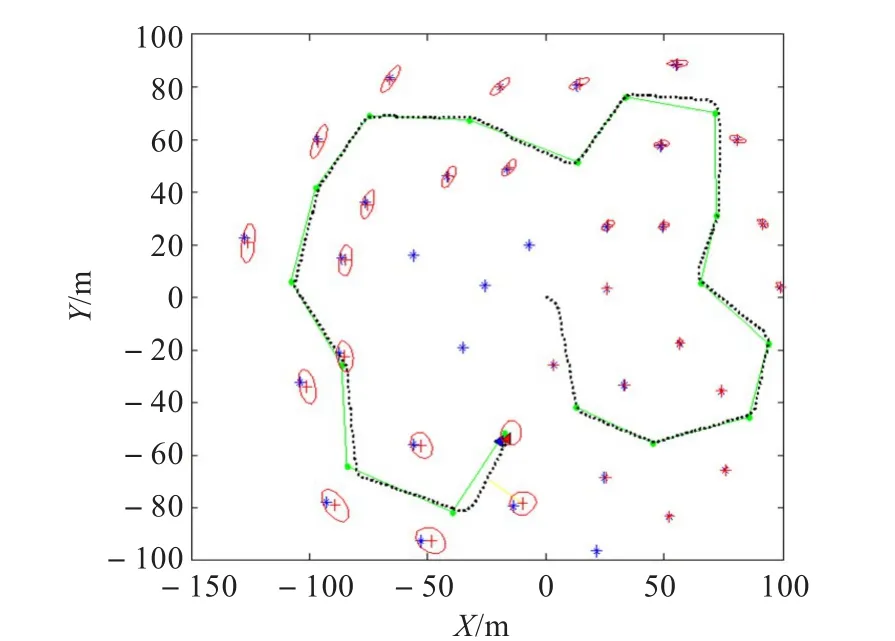
图2 UKF-SLAM仿真结果

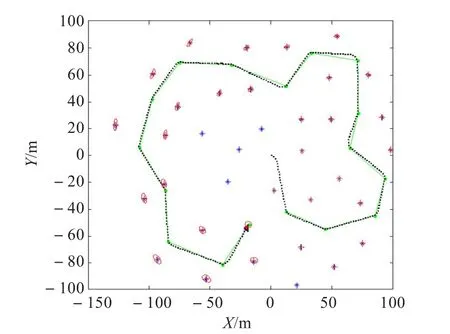
图3 SR-UKF-SLAM仿真结果

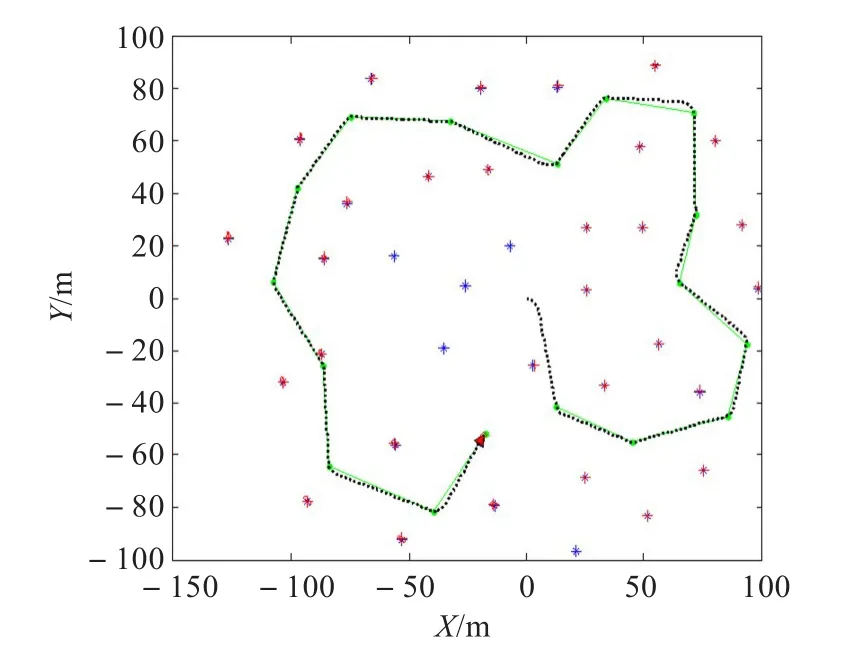
图4 SPSR-UKF-SLAM仿真结果

机器人探索一圈历时330 s左右，进行多次实验取均值。本文取其前300 s的仿真结果进行数据分析。图5（a）、（b）、（c）分别为UKF-SLAM算法、SR-UKF-SLAM算法以及SR-UKF-SLAM算法在机器人位姿的x方向、y方向以及航向角的误差对比图。从图中可以看出，三种算法对机器人位姿估计的误差均呈上升趋势，但对比于前两种算法，SR-UKF-SLAM算法的估计误差相对平稳，并保持较低的水平。以上的实验结果均表明，SPSR-UKF-SLAM算法在降低计算复杂度的同时，也提高了机器人位姿的估计精度。

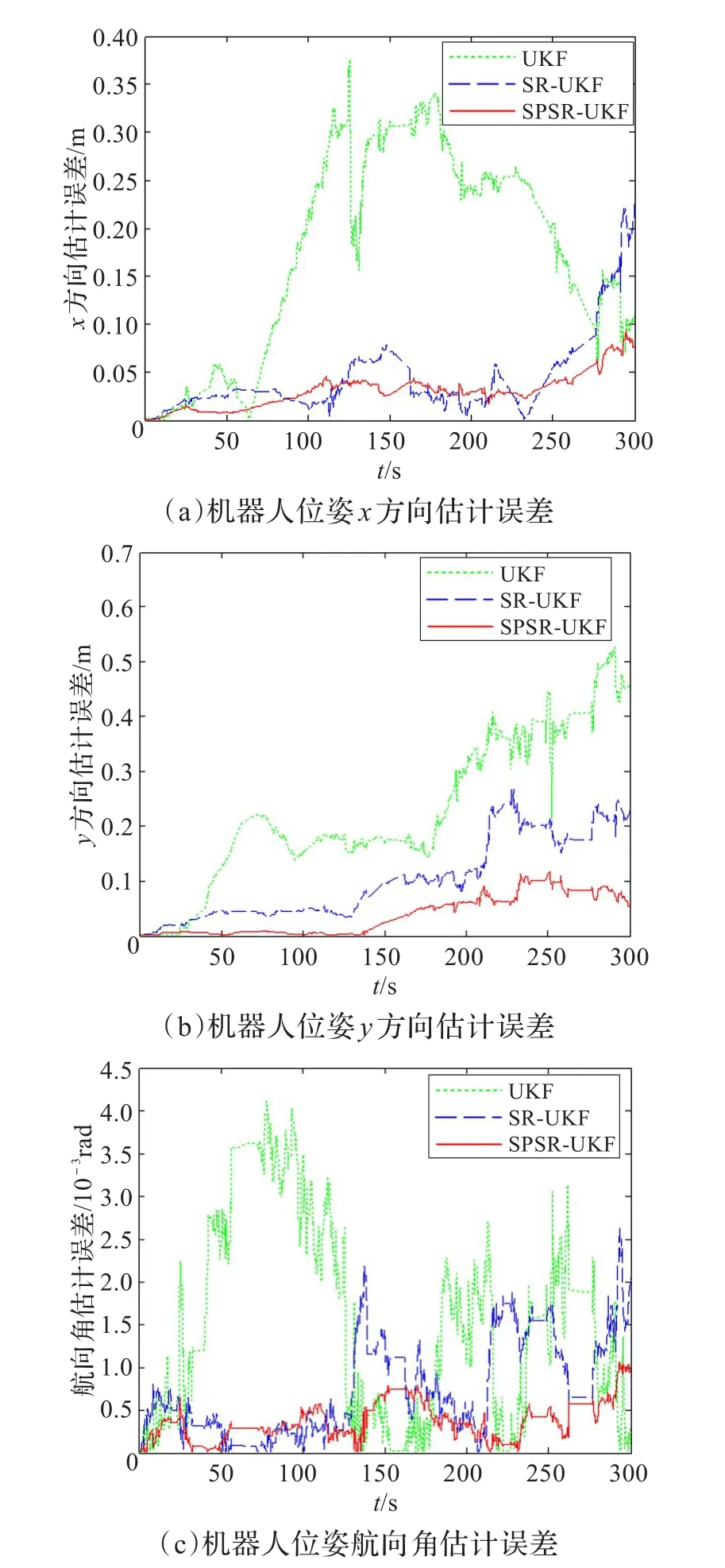
图5 三种算法的估计误差对比

为了更直观地对比三种SLAM算法的性能，分别计算三种算法的平均误差，如表1所示。从表1中的数据得知，三种算法中，SPSR-UKF-SLAM算法的机器人位姿估计精度最高。与SR-UKF-SLAM算法相比，SPSRUKF-SLAM算法在机器人位姿的x方向、y方向以及航向角的误差分别降低了19.08%、29.31%、50.47%。

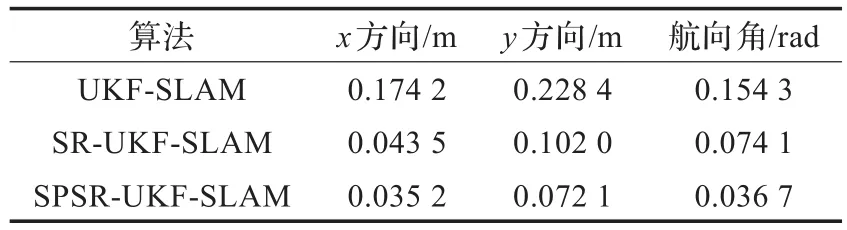
表1 算法误差统计比较

5 结论

根据UKF-SLAM算法存在的计算机的舍入误差带来的滤波器发散，使用协方差平方根更新替代协方差更新；并针对对称采样的采样点较多，实时性差且易产生非局部效应等问题，变换采样策略为比例最小偏度单行采样，从而提出了更为优化的SR-UFK-SLAM算法。经过MATLAB仿真实验表明，SPSR-UKF-SLAM算法与UKF-SLAM算法相比，可以有效地提高机器人位姿的估计精度，以及特征地图的估计准确度，且计算复杂度相对较低，并具有更好的稳定性。

[1]王璐，蔡自兴.未知环境中移动机器人并发建图与定位（CML）的研究进展[J].机器人，2004，26（4）：380-384.

[2]Sm ith R C，Cheeseman P.On the representation and estimation of spatial uncertainty[J].Robotics Research，1986，5（4）：231-238.

[3]Sm ith R，Self M，Cheesseman P.Estimating uncertain spatial relationships in robotics[C]//Proc of Conf Uncertainty in Artificial Intelligence，1988：435-461.

[4]吕太之.一种新的抗外部干扰EKF-SLAM算法[J].计算机工程，2012，38（21）：1-4.

[5]张海强，窦丽华，方浩，等.基于压缩型EKF的SLAM改进算法[J].系统仿真学报，2009，21（18）：5668-5680.

[6]周武，赵春霞，沈亚强，等.基于全局观测地图模型的SLAM研究[J].机器人，2010，32（5）：647-654.

[7]李秀才，郑志强，张辉.SLAM问题中机器人定位误差分析与控制[J].自动化学报，2008，34（3）：323-330.

[8]张恒，樊晓平，刘艳丽.移动机器人同时定位与地图构建研究进展[J].数据采集与处理，2005，20（4）：458-465.

[9]Julier S J，Uhlmann J K，Durrant-Whyte H.A new method for the nonlinear transformation of means and covariances in filters and estimation[J].IEEE Transactions on Automatic Control，2000，45（3）：477-482.

[10]石杏喜，赵春霞，郭剑辉.基于PF/CUKF/EKF的移动机器人SLAM框架算法[J].电子学报，2009（8）：1865-1868.

[11]Merwe R V D，Wan E A.The squre-root unscented Kalman filter for state and parameter-estimation[C]//International Conference on Acoustics，Speech，and Signal Processing，Utah，2001.

[12]杨静，郑南宁.一种基于SR-UKF的GPS/DR组合定位算法[J].系统仿真学报，2009，21（3）：721-722.

[13]安雷，张国良，汤文俊.基于RSSI的机器人室内卡尔曼滤波定位算法[J].计算机工程与应用，2012，48（8）：230-232.

[14]李树荣，倪鹏飞.基于平方根UKF的SLAM算法[J].计算机工程与应用，2011，47（22）：209-212.

[15]石杏喜，赵春霞.基于概率的移动机器人SLAM算法框架[J].计算机工程，2010，36（2）：31-32.

[16]Julier S J，Uhlmann J K.Reduced sigma point filters for propagation of means and covariances through nonlinear transformation[C]//Proc of American Control Conf，Jefferson City，2002：887-892.

WANG Guidong, CHEN Yuedong, CHEN Mengyuan

Anhui Key Laboratory of Electric Drive and Control, Anhui Polytechnic University, Wuhu, Anhui 241000, China

Due to the distortion of filter gain matrix and high calculation complexity associating with nonlocal effect if symmetric sampling is adopted in the UKF-SLAM algorithm, the UKF-SLAM algorithm adopting square root and single row sampling method based on the proportion and mini-skewness is proposed. The advanced algorithm puts the square root of covariance matrix into iterative computation instead of covariance matrix and adopts the optimized single row sampling strategy based on the proportion and mini-skewness. The experimental results show the algorithm can improve the estimation accuracy of feature map and the pose of robot, besides, that can reduce the complexity and increase stability of the algorithm.

filter gain; sampling strategy; square root; computational complexity

WANG Guidong, CHEN Yuedong, CHEN Mengyuan. UKF-SLAM algorithm adopting square root and single row sampling method based on proportion and mini-skewness. Computer Engineering and Applications, 2014, 50（17）：63-67.

A

TP24

10.3778/j.issn.1002-8331.1404-0132

安徽省自然科学基金（No.11040606M 153）；安徽高校省级自然科学研究项目（No.KJ2013A 041）。

汪贵冬（1990—），男，硕士在读，研究领域为无线传感器网络；陈跃东（1956—），通讯作者，男，教授，硕导，研究领域为运动控制系统与检测技术；陈孟元（1984—），男，讲师，研究领域为无线传感器网络。E-mail：76920395@qq.com

2014-04-09

2014-05-30

1002-8331（2014）17-0063-05