改进的乘幂适应度函数在遗传算法中的应用

杨水清，杨加明，孙超

南昌航空大学飞行器工程学院，南昌 330063

改进的乘幂适应度函数在遗传算法中的应用

杨水清，杨加明，孙超

南昌航空大学飞行器工程学院，南昌 330063

在遗传算法优化过程中，引导搜索的主要依据是适应度函数。通过评估常见的几种适应度函数，兼顾保持种群的多样性和算法的收敛性，由乘幂尺度变换，提出了一种改进的乘幂适应度函数。以三个典型的测试函数为例，在相同遗传操作和参数情况下，分别采用常见的与改进的适应度函数进行优化比较。结果表明，所改进的乘幂适应度函数能明显提高算法的收敛精度、收敛速度和收敛稳定性，对提高遗传算法的整体性能有重要的意义。

遗传算法；适应度函数；测试函数；优化计算

1 引言

求解复杂函数的最优问题是遗传算法（Genetic A lgorithms，GA）的一个重要研究方向。Holstien[1]首先在纯数学优化领域应用GA。De Jong[2]在函数优化方面进行了深入研究，并对一些具有代表性的测试函数进行了算法优化实验。20世纪80年代末，Goldberg[3]对适应度函数做了进一步分析，发现目标函数经过线性变换后，可作为一种较好形式的适应度函数。

在遗传算法中，适应度（Fitness）用来度量群体中的个体在优化计算中达到或接近于最优解的优良程度[4]。适应度较高的个体遗传到下一代的概率就较大；而较低的个体遗传到下一代的概率就相对小一些。遗传算法引导搜索的主要依据就是个体的适应度值。也就是说，遗传算法依靠选择操作来引导算法的搜索方向。选择操作是以个体的适应度作为确定性指标，从当前群体中选择适应度值高的个体进行交叉和变异，寻找最优解。

如果适应度函数选择不当，可能会造成遗传算法的欺骗现象[5]，因此适应度函数的选取至关重要，它直接影响到遗传算法的收敛速度以及能否找到最优解。遗传算法的多数改进方案主要针对适应度函数、遗传操作算子、控制参数的选择及编码。文献[6]提出的自适应遗传算法对交叉概率pc和变异概率pm进行自适应调整，其方案建立在个体适应度的基础之上。

已有研究[7-13]表明，适应度函数的改进对遗传算法优化有积极影响。本文以函数最优化问题为背景，在现有研究的基础上对适应度函数作进一步改进，利用乘幂变换法的特点，结合适应度线性尺度变换，提出了基于乘幂变换的非线性动态适应度函数，用典型的遗传算法测试函数[14]验证本文提出的适应度函数的有效性与可行性。

2 适应度函数的选择

2.1 适应度函数的作用

对遗传算法进行选择操作时，往往会出现两个遗传算法的欺骗问题：

（1）在遗传进化的初期，通常会产生一些超常的个体，若按照比例选择法，这些超常个体会因竞争力突出而控制选择过程，影响算法的全局优化性能。

（2）在遗传进化的后期，即算法接近收敛时，由于种群中个体适应度差异较小，继续优化的潜能降低，可能获得某个局部最优解。

如果适应度函数设计不当，有可能造成这两种问题的出现，所以适应度函数的设计是遗传算法设计的一个重要内容。

2.2 适应度函数的分析

适应度函数的设计应尽量满足如下条件：

（1）单值、连续、非负、最大化。

（2）合理、一致性，要求适应度值反映对应解的优劣程度。

（3）计算量小。适应度函数设计应尽量简单，这样可以减少计算时间和算法的复杂性。

（4）通用性较强。适应度对某类具体的问题，应尽可能通用，最好无需改变适应度函数中的参数。

2.2.1 基本适应度函数（BGA）

（1）直接以待解的目标函数f(x)转化为适应度函数Fit(f(x))，这种适应度函数简单直观，即

其中，f(x)为目标函数最大化问题；-f(x)为目标函数最小化问题。但有可能出现两种现象：一是不能满足常用的赌盘选择中概率非负的要求；二是某些待解函数在函数值分布上相差很大，由此得到的平均适应度不利于体现种群的平均性能，从而影响算法的性能。

（2）对于求最小值问题，可以做下列转换：

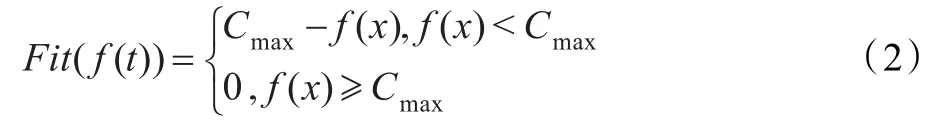
式中，Cmax为一个适当的相对较大的数，它是f(x)的最大估计值。

对于求最大值问题，做下列转换：

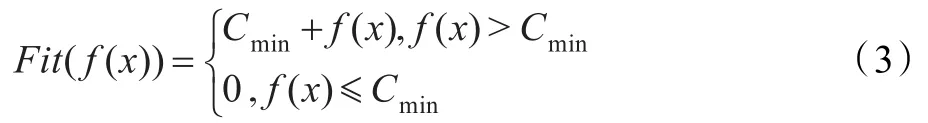
式中，Cmin为f(x)最小估计值，它可以是一个合适的输入值。这种方法是第一种方法的改进，可以称为“界限改造法”，但这种方法有时存在界限值预先估计困难，导致计算结果不精确。

2.2.2 乘幂适应度函数（EGA）

乘幂尺度变换是指新的适应度为原来适应度的某个指定乘幂，其乘幂尺度变换的公式为：

式中，F′是经过乘幂变换后得到的新适应度函数；F是原适应度函数，可直接取目标函数。幂指数k与所求的问题有关，在算法的执行过程中需要不断对其进行修正，才能使尺度变换满足一定的伸缩要求。

2.2.3 改进的乘幂适应度函数（MGA）

改进的新适应度函数如下：

式中，F′是经过乘幂变换后得到的新适应度函数；F是原适应度函数；Cmax是最大估计值，可直接取目标函数。此时k不再是一个常数，而是一个随进化代数增加的非线性动态变化的正数。t是当前的进化代数；T是最大的遗传代数；Favg是当代种群的平均值；ξ是适当大小的数。

3 测试与分析

3.1 测试函数

函数1定义为：

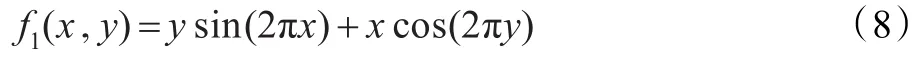
该函数是一个非线性、不对称、不可分离的多峰函数，其中x，y的区间均为[-2，2]。全局有多个极值点，较难找到最优点。其三维形状如图1所示，图中的圆圈表示各代种群搜寻到的最优解。

互联网大数据支持下的“共享经济模式”，同时影响着现代城市的建设与发展，使智慧城市建设步入以大数据中心为背景的“共享时代”，同时也为智慧城市在我国的建设与发展开创了新局面，智慧城市在大数据平台的支撑下，会得到更好的发展[1]。

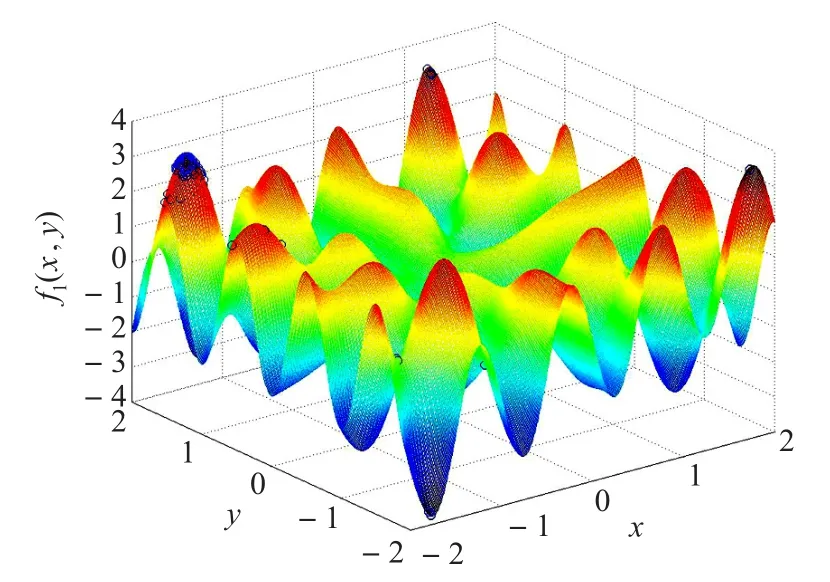
图1 函数1的分布图

函数2又称为Shubert函数，定义为：

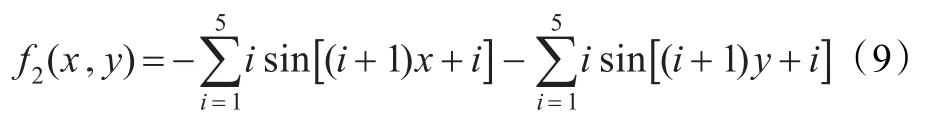
该函数是一个复杂的二维函数，(x，y)的取值区间为[-10，10]，可以看出有很多的极大值点，由于该函数具有强烈的震荡形态，所以找到全局极大值有一定的困难。其三维形状如图2所示，图中圆圈表示各代种群搜寻到的最优解。

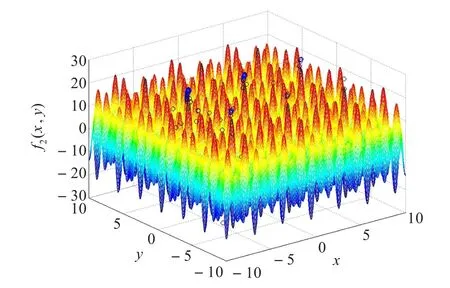
图2 函数2的分布图

函数3又称为Rastrigrin函数，定义为：

f3(x，y)=20+x2-10 cos(2πx)+y2-10 cos(2πy)（10）

该函数是复杂的二维函数，具有很多的极值点，(x，y)的取值区间为[-5，5]，三维形状如图3所示，图中圆圈表示各代种群搜寻到的最优解。

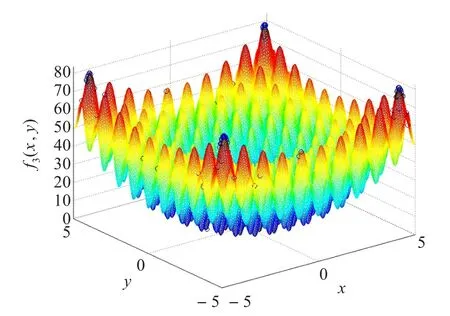
图3 函数3的分布图

3.2 测试结果与分析

为了便于比较各算法搜索的性能，选取同样的测试参数比较。本文选择种群规模为100；进化代数为60；交叉概率为0.7；变异概率为0.01；代沟（GGAP）为0.95，采用进化代数固定的终止策略。对每个适应度函数算法分别运行50次，实验测试的结果保留四位有效数。为了验证MGA的有效性和可行性，将其与BGA以及EGA进行了对比。

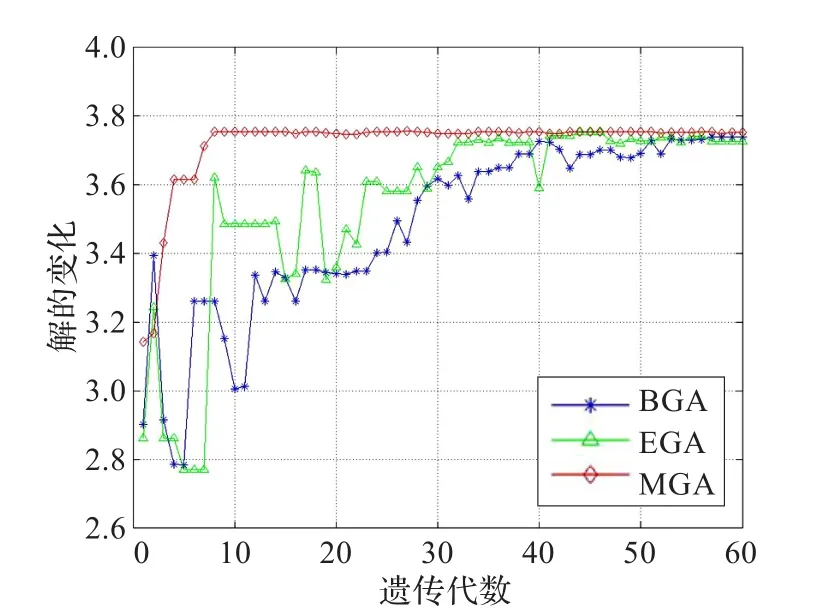
图4 函数f1(x，y)在不同算法下解的变化对比

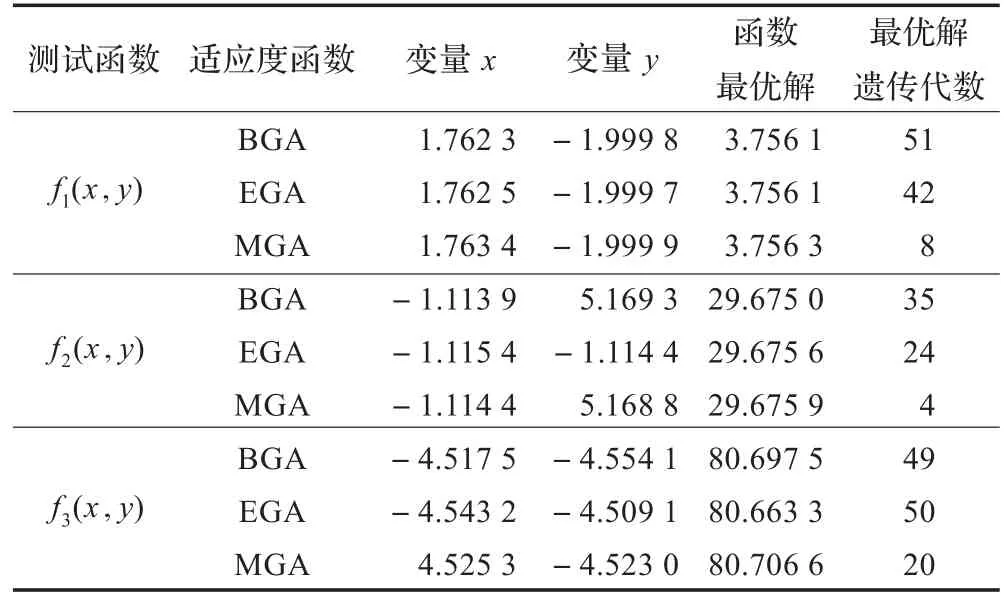
表1 测试实验的最优结果

下面讨论MGA、EGA和BGA之间的收敛速度、收敛精度和收敛稳定性的优劣。

图4、图5和图6分别为函数f1(x，y)、f2(x，y)和f3(x，y)在不同算法下解的变化对比，从图4可以看出，虽然BGA、EGA和MGA最后都能收敛到最优解，但MGA的收敛速度要明显快于BGA和EGA。由图5及图6知道，MGA很快收敛到最优解；而EGA和BGA收敛波动性较大，且它们在遗传进化的后期才收敛于最优解。

图7、图8和图9分别为函数f1(x，y)、f2(x，y)和f3(x，y)在不同算法下运行50次得到的最优解变动对比。从图7中可以看出，BGA和EGA算法每次运行得到的最优解变动非常大，尤其是BGA；而且它们的最优解的精确度不高。故在收敛精度和收敛稳定性方面，EGA要优于BGA；MGA要优于BGA和EGA。类似的结论反映在图8和图9上，MGA算法每次运行所得的最优解几乎在一条直线上，而EGA和BGA的变动较大。

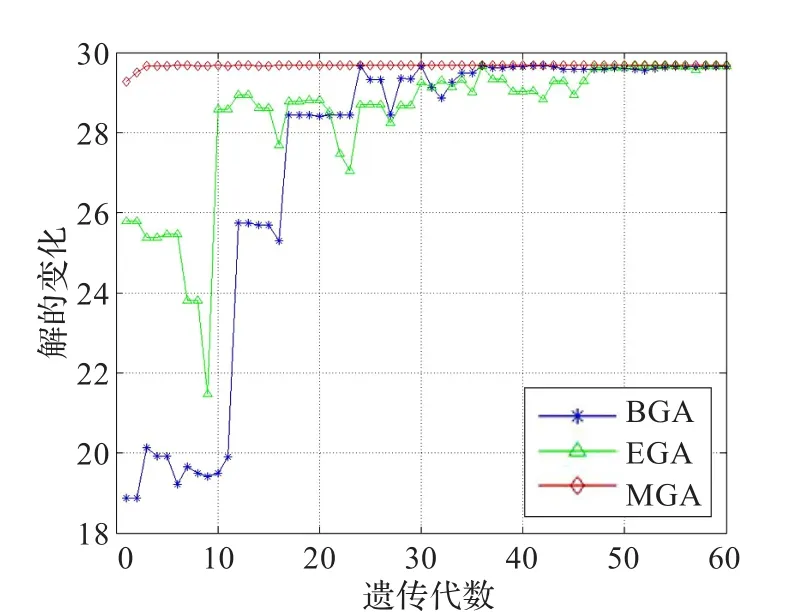
图5 函数f2(x，y)在不同算法下解的变化对比

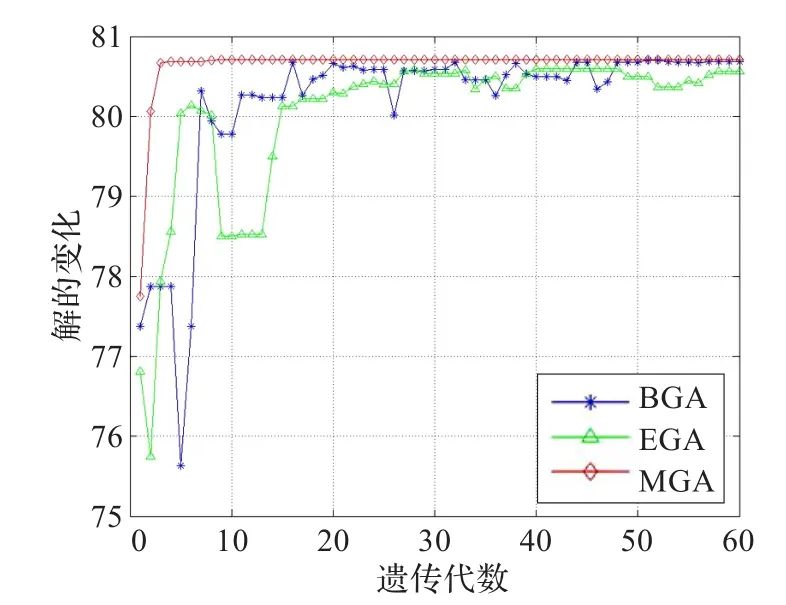
图6 函数f3(x，y)在不同算法下解的变化对比

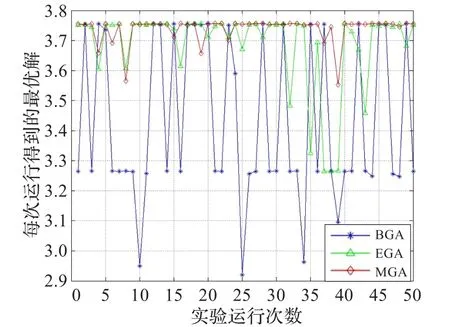
图7 函数f1(x，y)在不同算法下最优解的变动对比

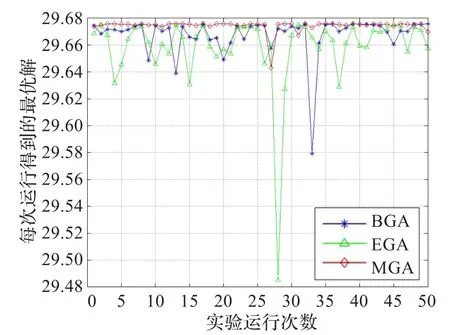
图8 函数f2(x，y)在不同算法下最优解的变动对比

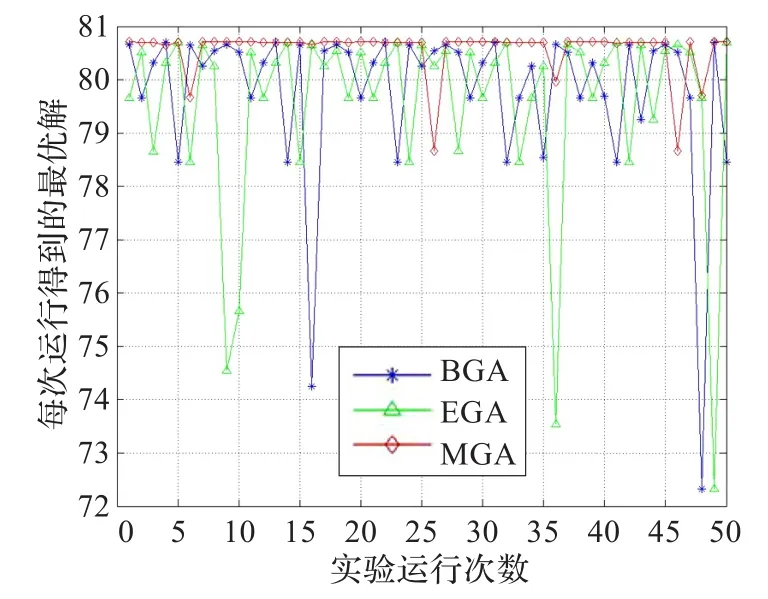
图9 函数f(x，y)在不同算法下最优解的变动对比

对于测试函数f1(x，y)，结合图4和图7，可以得出结论，在收敛速度、收敛精度及收敛稳定性方面，MGA均优于BGA和EGA。对于测试函数f2(x，y)和f3(x，y)，分别结合图5、图6和图8、图9，可以得出如下结论，在收敛速度、收敛精度以及收敛稳定性方面，MGA具有明显优势。

需要特别指出的是，图7和图9相对于图8而言，其最优解的变动明显较大，可能的原因有：（1）测试函数f2(x，y)的局部极大值点太多，且极值相差不大，故对一般的适应度函数较容易找出局部最优解。从图1和图3可以看出，图中极值点相对较少，且差距明显，故设计更好的适应度函数会更容易找到最优解。（2）乘幂变换法对于幂指数及一些相关参数有一定的选择要求，这就需要在程序执行过程中通过分析选取不同的幂指数。

4 结论

寻到较精确最优解；在收敛速度方面，MGA算法明显提高。

（2）对每种算法运行50次，MGA算法运行所得的最优解变动很小，而BGA和EGA算法得到的最优解变动幅度明显，说明在收敛精度和收敛稳定性方面，MGA算法优势明显。

（3）适应度函数标定只是遗传算法优化问题的改进措施之一，还须注重编码方案、遗传操作方式及相关控制参数等。

本文用三种测试函数对改进的遗传算法的性能进行测试，以一般适应度函数（BGA、EGA）遗传算法和改进的乘幂适应度函数（MGA）遗传算法进行性能比较，得到以下结论：

（1）对三种测试函数，MGA算法很快地找到了精确最优解，而BGA和EGA算法基本是在遗传进化后期搜

[1]Holstien R B.Artificial genetic adaptation in computer control systems[D].Ann Arbor：Department of Computer and Communication Sciences，University of Michigan，1971.

[2]De Jong K A.Analysis of the behavior of a class of genetic adaptive systems[D].Ann Arbor：Department of Computer and Communication Sciences，University of Michigan，1975.

[3]Goldberg D E.Genetic algorithms in search，optimization and machine learning[M].Boston，MA，USA：Addison Wesley Publishing Company，1989：117-121.

[4]孙树栋，周明.遗传算法原理及应用[M].北京：国防工业出版社，2002.

[5]雷英杰，张善文，李续武，等.MATLAB遗传算法工具箱及应用[M].西安：西安电子科技大学出版社，2005.

[6]邓洋春，梁昔明.一种改进操作算子的加速收敛遗传算法[J].现代电子技术，2009（2）：36-38.

[7]郭晓原.遗传算法中适应度尺度变换与操作算子的比较研究[D].北京：华北电力大学，2012.

[8]金芬，孙春华.遗传算法中适应度函数的改进[D].江苏苏州：苏州大学，2010.

[9]张思才，张方晓.一种遗传算法适应度函数的改进方法[J].计算机应用与软件，2006，23（2）：146-150.

[10]伊丹丹，姜淑娟，张艳梅.多路径覆盖测试数据生成适应度函数设计方法[J].计算机工程与应用，2012，48（22）：79-83.

[11]代才，王宇平.基于新的适应度函数的多目标进化算法[J].华中科技大学学报，2013，41（7）：56-60.

[12]施泽波.图像增强中优化算法适应度函数设计[J].电光与控制，2010，20（5）：113-117.

[13]王伟，轩红.基于AHP方法的遗传算法适应度函数设计与应用[J].河南科学，2010，28（9）：59-64.

[14]史峰，王辉，郁磊，等.MATLAB智能算法30个案例分析[M].北京：北京航空航天大学出版社，2011.

YANG Shuiqing, YANG Jiaming, SUN Chao

School of Aircraft Engineering, Nanchang Hangkong University, Nanchang 330063, China

It is the main factors for fitness functions to guide the search of the genetic algorithm optimization process. The exponential fitness functions are improved by exponentiation scale transformation.They are used to evaluate several common fitness functions to keep their diversity of population and convergence of the algorithm s.The optimal computation is compared for the usual and the improved fitness functions under the same conditions of genetic manipulation and their parameters in using three typical test functions.Numerical results show that it is significant for the new fitness functions of a power optimal algorithm to improve the overall performance including the accuracy,convergence speed,and convergence stability of the ameliorated genetic algorithm s.

genetic algorithm s;fitness functions;testing functions;optimal computation

YANG Shuiqing, YANG Jiaming, SUN Chao. Improved exponentiation scale transformation in application of genetic algorithm. Computer Engineering and Applications, 2014, 50（17）：40-43.

A

TP18

10.3778/j.issn.1002-8331.1311-0047

航空科学基金（No.2012ZA 56001）；江西省自然科学基金（No.20114BAB202010）。

杨水清（1988—），男，硕士，主要研究方向为数值分析与计算；杨加明（1963—），男，博士，教授，主要研究方向为复合材料结构分析与设计；孙超（1988—），男，硕士，主要研究方向为复合材料结构分析。E-mail：happyeveryday1115@163.com

2013-11-05

2014-02-24

1002-8331（2014）17-0040-04

CNKI网络优先出版：2014-04-01,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1311-0047.htm l