稳健的全阵波束形成方法

汪扬，赵知劲，2，刘晓莉，2

1.杭州电子科技大学通信工程学院，杭州 310018

2.中国电子科技集团第36研究所通信系统信息控制技术国家级重点实验室，浙江嘉兴 314001

稳健的全阵波束形成方法

汪扬1，赵知劲1，2，刘晓莉1，2

1.杭州电子科技大学通信工程学院，杭州 310018

2.中国电子科技集团第36研究所通信系统信息控制技术国家级重点实验室，浙江嘉兴 314001

由于相干干扰和角度估计误差影响波束形成性能，对此提出一种稳健的波束形成方法。采用加权空间平滑算法去除相干性；对期望信号施加约束，保证一定角度估计误差范围内算法的稳健性；进行全阵波束形成变换，避免阵列孔径损失。仿真结果表明，在相干干扰环境中，该算法的方向图在期望信号方向有明显主瓣，有利于接收期望信号；在一定的角度估计误差范围内，该算法可保持比较高的且比较平坦的输出信干噪比；随着输入信噪比的增加，输出信干噪比几乎线性增大。

自适应波束形成；相干干扰；稳健性；阵列孔径

1 引言

在自适应阵列处理中，由于多径效应或人工干扰的存在使期望信号与干扰相干，直接应用常规波束形成将引起期望信号相消[1]，使波束形成性能急剧下降[2-3]，因此存在相干干扰时的自适应波束形成技术已引起人们的广泛关注。有相干干扰时的波束形成方法主要是分子阵波束形成方法与全阵波束形成方法两大类。空间平滑算法[4-7]是克服相干干扰环境下期望信号相消现象的一种经典子阵波束形成方法，由于经典空间平滑算法[8]以恢复信号干扰空间的秩为基础，没有利用期望信号与干扰的互相关函数，所以去相干比较粗糙。加权空间平滑算法（AWSS）[9]从互相关函数出发，以使期望信号与干扰互相关函数为零为准则，从根本上去除相干性。这类方法可以很好地去除相干性，缺点是孔径损失较大，阵列分辨率下降；另外，由于它们未考虑算法的稳健性，即使去除了相干性，但角度估计误差仍会导致最终性能不佳。全阵波束形成方法阵列孔径大、分辨率高，包括对相干干扰施加强约束[10]、对接收数据进行预处理变换[11]、裂相变换[12]或变换投影[13]等方法，它们可以较好地去除相干性，但需要知道期望信号、干扰信号的波达方向，使计算量增加，同时算法对信号角度估计的偏差较敏感。文献[14]（SS-Toeplitz算法）先通过空间平滑子阵波束形成，再利用子阵间相位关系，转为全阵波束形成。该方法去相干性强，阵列孔径大，但对期望信号角度估计敏感。针对以上两类方法存在的问题，本文提出一种稳健的全阵波束形成方法，先通过加权空间平滑很好地去除相干性，然后采用对期望信号角度估计的约束，降低角度估计误差的影响，最后转化到全阵进行波束形成，以保持阵列孔径不变。该算法在相干干扰环境中，稳健性强，有效孔径大。

2 自适应加权空间平滑算法

2.1 信号模型

一个N元等距线阵，间距为d，各阵元均为各向同性，远场处有1+P+K个窄带同频信号以平面波入射，包括一个期望信号、P个相干干扰信号、K个不相干干扰信号，它们的到达角度分别为θ0、θi(i=1，2，…，P)、θi(i=P+1，P+2，…，P+K)，则阵列接收信号为：

式中X(t)为N×1快拍信号矢量，X(t)=[x1(t)，x2(t)，…，xN(t)]T。

si(t)(i=0,1,…,P+K)为信号复包络，α(θi)=[1,ejβi,…, ej(N-1)βi]T，i=0，1，…，P+K为第i个信源的导向矢量，βi=(2π/λ)dsin(θi)。n(t)为N×1的阵列高斯白噪声矢量，n(t)=[n1(t)，n2(t)，…，nN(t)]T与所有信号均不相关，且功率均为。令AN=[α(θ0)α(θ1)…α(θP+K)]，S(t)= [s0(t)s1(t)…sP+K(t)]T，则接收信号可表示为：X(t)= ANS(t)+n(t)[15]。

X(t)的相关矩阵为：

其中RS=E[S(t)SH(t)]为信号干扰相关矩阵，IN为N维单位阵。

2.2 加权空间平滑算法原理

将阵列分为相互重叠的L个子阵，每个子阵的阵元个数为m=N-L+1，设Rk为第k个子阵的协方差矩阵，则加权空间平滑算法的等价m维阵列协方差矩阵为：

其中WS=[w(1)，w(2)，…，w(L)]T为子矩阵的加权矢量，需满足式（4）：

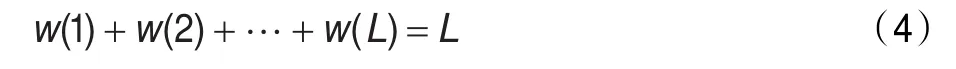
加权空间平滑后等效信号干扰相关矩阵为Rwfs，Rwfs的第(i，j)个元素[9]为：

其中Δβi，j=βi-βj=-Δβj，i。

令α(θV，j)=[1，ejΔβ0，j，…，ej(L-1)Δβ0，j]T，它具有范德蒙结构，可看做是第j个虚拟干扰源的导向矢量，干扰角度为θV,j,Δβ0,j=(2π/λ)dsin(θV,j)，Δβj,0=-Δβ0,j=(2π/λ)dsin(-θV,j)。所以完全去相关条件为：

其中θV，0相当于虚拟期望信号的方向。

求解式（6）最优权向量的问题等效为当虚拟期望信号在0°方向且有2×(P+K)个互不相关干扰从角度θV，j，-θV，j(j=1，2，…，P+K)入射到L元虚拟阵列上时，自适应波束形成最优权值WS_opt的求解问题。

2.3 移相变换与构造镜像干扰

假设L元阵列信号X(t)中期望信号方向θ0已经估计得到，构造移相变换矩阵BL=diag(1,e-jβ0,…,e-j(L-1)β0)，其中β0=(2π/λ)dsin(θ0)。对阵列信号进行如下变换：Y(t)=BLX(t)，则变换后的阵列协方差矩阵为：

Δβj，0=-Δβ0，j=(2π/λ)dsin(-θV，j)。由此可知，移相变换后的阵列信号Y(t)中期望信号在0°方向，干扰在-θV，j方向。若求RY，real=real(RY)，则相当于在阵列信号Y(t)中增加了θV，j方向的干扰。

所以，自适应加权空间平滑算法AWSS步骤如下：

（1）对N元的阵列接收信号X(t)进行空间平滑，子阵元数取为L，得平滑后的阵列协方差矩阵R′（L×L矩阵）。

（2）移相变换和构造镜像干扰，得RY=BLR′BHL，对RY取实部，得RY，real=real(RY)。

（3）由构造出的协方差矩阵RY，real求虚拟波束形成的最优权矢量WS_opt为：

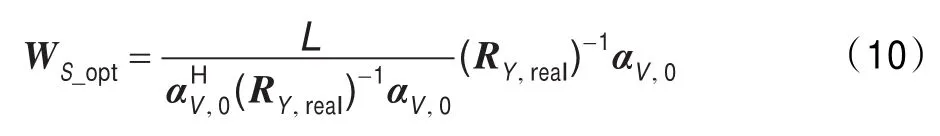
其中α(θV，0)=[1，1，…，1]T（L×1维）。

（4）将式（10）的WS_opt代入式（3）求出等价的m维阵列协方差矩阵Rwf。

（5）将Rwf用于求自适应阵列的m×1维权向量：

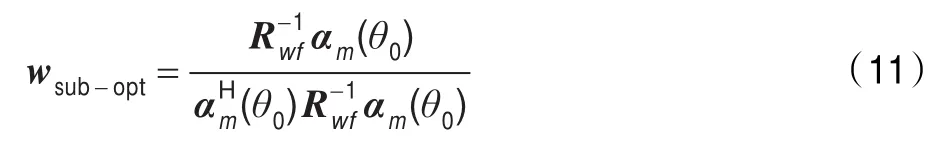
其中αm(θ0)=[1，ejβ0，…，ej(m-1)β0]T。

AWSS算法去除了等价m维阵列协方差矩阵Rwf中的信号相干性，但自适应阵列权向量wsub-opt完全依赖于αm(θ0)，即wsub-opt对期望信号方向θ0估计误差很敏感，算法的稳健性较差；另外，损失了阵列孔径，恶化了分辨率。

3 稳健的全阵波束形成方法

为了提高算法的稳健性和分辨率，保持阵列孔径不减小，本章研究稳健的全阵波束形成方法（RAWSS）。

3.1 最差性能最优的稳健方法

定义期望信号导向矢量为α0，它所属的集合为：

对Α0内的所有导向矢量均约束阵列响应的绝对值大于等于1，可保证即使在最差的条件下，期望信号仍有无失真响应。

最差性能最优的稳健算法[16]优化问题如下：

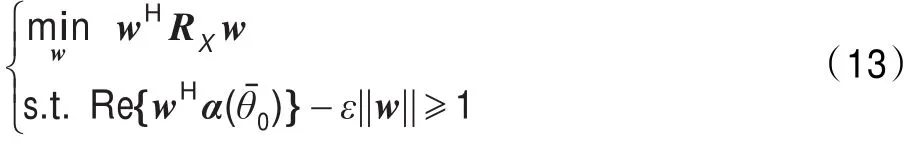
3.2 全阵波束形成

利用文献[14]方法，考虑各子阵之间相位连续递增性，在得到子阵最优权向量wsub-opt后，使用如下的矩阵变换，得到全阵的权向量，以避免孔径损失。

将子阵的m个权值直接赋给全阵的前m个阵元；再把子阵往后移一个阵元，此时对子阵的m个权值作γ的相位递增，将递增后的m个权值赋给全阵从第二个阵元开始的m个阵元；然后再移动子阵，依次类推；直到子阵的最后一个权值对齐并赋给全阵的最后一个阵元。最后将全阵每个阵元上的所有权值相加，即得到用于全阵的权值wfull-opt。

令矩阵：

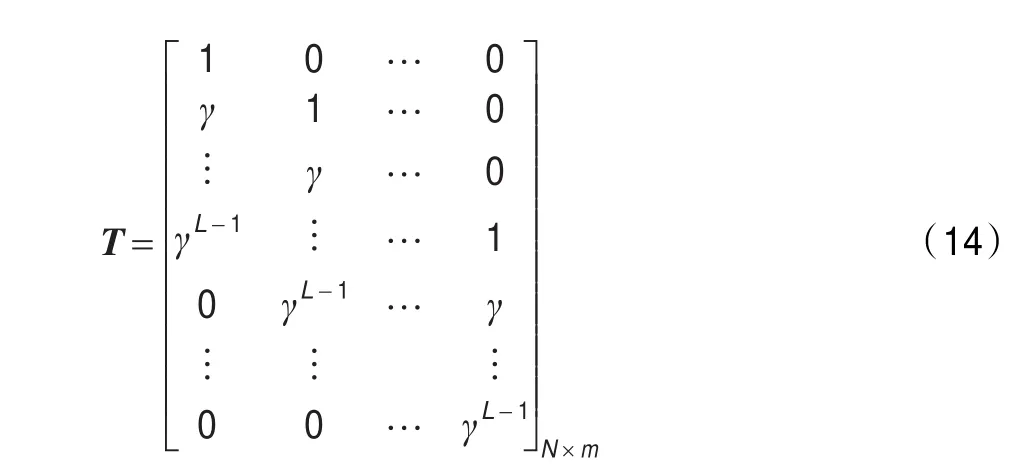
至此，得到的wfull-opt是原始阵列全部阵元的权值。

利用加权空间平滑算法可有效去除信号的相干性、最差性能最优的稳健方法对期望信号角度估计误差的稳健性和全阵波束形成能保持阵列孔径的特性，本文提出了一种稳健的全阵波束形成方法（RAWSS），算法步骤如下：

（1）由AWSS算法的步骤（1）～（4）求Rwf。

（2）由下式求得最佳子阵权值wsub-opt：

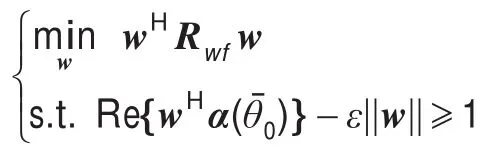
其中ε为自行设定的参数，理论上是取得越大越好。在仿真实验中，由于阵元数有限，ε不宜取得过大。本文中取3。

（3）由式（14）、式（15）求得原始阵列的最佳权值wfull-opt。

该方法保持了原全阵的阵列孔径，具有较强的抗相干干扰能力和对角度估计误差稳健性。

4 仿真分析

设天线阵为16元等距线阵，阵元间距为0.5倍的波长，有一个期望信号、一个相干干扰、一个非相干干扰，角度方向分别为θ0=0°、θ1=-20°、θ2=40°。相干干扰与期望信号完全相干，期望信号的信噪比（下文未特别说明时）为10 dB，非相干干扰的干噪比为30 dB，高斯白噪声的功率σ2n为1，快拍数为512次。期望信号的方向角估计精度范围为[θ0-1°，θ0+1°]，本章分析比较SS-Toeplitz[14]、AWSS[9]、本章提出的RAWSS算法的性能。

信噪比、干噪比、输出信干噪比定义如下：

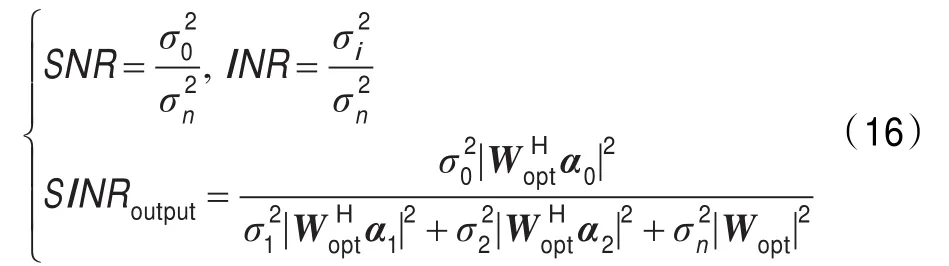
图1 阵列输出SINR随角估计误差的变化

当角度估计误差为1°和2°、SNR为10 dB、ε在[2，3.5]之间变化时，RAWSS算法的阵列输出信干噪比随ε值的变化如图1所示。当ε增加到3.1以后，算法求不出最优权值。这是由于实际中阵元数有限，自由度就有限。当ε值取得越大，用于保证期望信号响应所需的自由度就越多，导致剩下用于约束干扰噪声响应的自由度就越少，从而找不出一个最优权值。由图1（a）可见，当角估计误差较大，随着ε增大，输出信干噪比增大，在ε=3左右，输出信干噪比接近最大。由图1（b）可见，当角估计误差较小，随着ε增大，输出信干噪比先增大后减小，在ε=3左右，输出信干噪比接近最大。因此，在本文RAWSS算法中，选取ε=3。

三种空间平滑算法的方向图如图2所示。由图可见，只有RAWSS算法在期望信号方向0°有主瓣，而另两种算法没有主瓣。

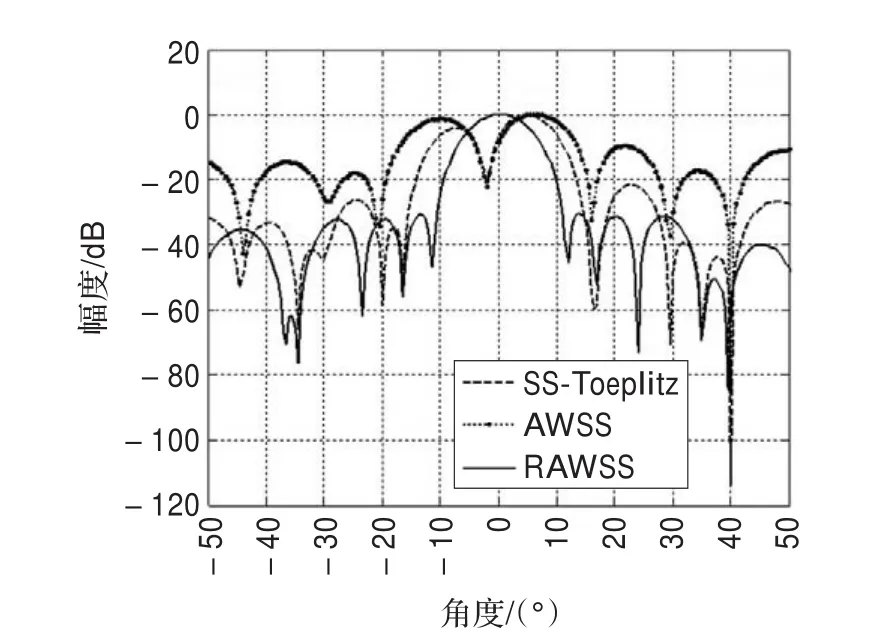
图2 几种空间平滑算法的方向图比较

三种算法的阵列输出信干噪比随角度估计误差的变化如图3所示。由图可见，无论SNR为0 dB或10 dB时，RAWSS算法在角度估计误差[-2°，2°]范围内，输出信干噪比均高于10 dB或20 dB，稳健性较强。而SSToeplitz和AWSS算法只在角度估计没有误差时，才有较高的输出信干噪比，当角度估计误差增大时，输出信干噪比下降迅速，算法的稳健性较差。

三种算法的输出信干噪比（SINR）随输入信噪比（SNR）的变化如图4所示。由图可见，当输入信噪比较小时，三种算法性能比较接近。对于RAWSS算法，由于最差性能最优稳健方法在有效保证期望信号响应同时，使得阵列输出功率最小，故干扰噪声响应很小，即：|WHα1|,|WHα2|<<|WHα0|。由式（16）可得：

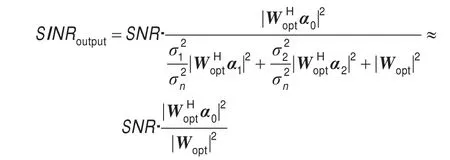
因此，在求出最优权值时，随着SNR的增大，RAWSS算法的输出信干噪比几乎线性增大；但SS-Toeplitz和AWSS算法对期望信号没有响应约束，故在输出信干噪比增大到一定程度时，开始下降。

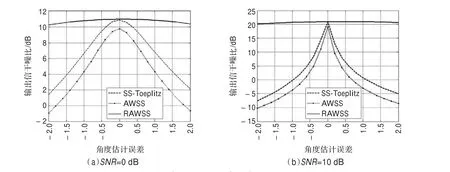
图3 阵列输出SINR随角度估计误差的变化

图4 阵列输出SINR随SNR的变化

5 结束语

针对相干干扰，本文提出了一种稳健的全阵波束形成方法。空间平滑、稳健约束、全阵波束形成多种技术相融合，该方法大大提高了阵列的相干干扰抑制能力，同时稳健性强、有效孔径大。

[1]Widrow B，Duvall K M，Gooch R P，et al.Signal cancellation phenomena in adaptive antennas：causes and cures[J]. IEEE Trans on Antennas and Propagation，1982，30（5）：469-478.

[2]Wax M，Anu Y.Performance analysis of the minimum variance beamformer[J].IEEE Trans on Signal Processing，1996，44（4）：928-937.

[3]Paulraj A，Reddy V，Kailath T.Analysis of signal cancellation due to multipath in optimum beamformers for moving arrays[J].IEEE Journal of Oceanic Engineering，1987，12（1）：163-172.

[4]Shan T J，Wax M，Kailath T.On spatial smoothing for direction-of-arrival estimation of coherent signals[J].IEEE Trans on Acoustics，Speech，and Signal Processing，1985，33（4）：806-811.

[5]Pillai S U，Kwon B H.Forward-backward spatial smoothing techniques for the coherent signal identification[J].IEEE Trans on Acoustics，Speech，and Signal Processing，1989，37（1）：8-15.

[6]Raghunath K J，Reddy V U.A note on spatially weighted subarray covariance averaging schemes[J].IEEE Trans on Antennas and Propagation，1992，40（6）：720-723.

[7]Elmaraazey M.An adaptive spatial smoothing technique for beamforming in the presence of correlated arrivals[C]// Proc of the IEEE International Symposium on Circuits and Systems.Chicago IL：IEEE Press，1993：208-211.

[8]Shan T J，Kailath T.Adaptive beamforming for coherentsignals and interference[J].IEEE Trans on Acoustics，Speech，and Signal Processing，1985，33（3）：527-536.

[9]丁前军，王永良，张永顺，等.一种虚拟波束形成自适应加权空间平滑算法[J].电子与信息学报，2006，28（12）：2263-2268.

[10]Yeh C C，Wang W D.Coherent interference suppression by an antenna array of arbitrary geometry[J].IEEE Trans on Antennas and Propagation，1989，37（10）：1317-1322.

[11]Sung L T，Tsai L T.Coherent interference suppression with complementally transformed adaptive beamformer[J]. IEEE Trans on Antennas and Propagation，1998，46（5）：609-617.

[12]Lu M，He Z Y.Adaptive beamforming using split-polarity transformation for coherent signal and interference[J]. IEEE Trans on Antennas and Propagation，1993，41（3）：314-324.

[13]赵永波，张守宏.存在相干信号时的最优波束形成[J].通信学报，2002，23（2）：113-121.

[14]周围，张德民，吴波，等.相干环境下LCMV自适应阵列抗干扰问题研究[J].电子与信息学报，2007，29（7）：1604-1607.

[15]王永良，丁前军，李荣峰.自适应阵列处理[M].北京：清华大学出版社，2009：177-181.

[16]Yu L，Liu W，Langley R J.Novel robust beamformers for coherent interference suppression with direction-ofarrival estimation errors[J].IET Microwaves Antennas and Propagation，2010，4（9）：1310-1319.

WANG Yang1,ZHAO Zhijin1，2,LIU Xiaoli1，2

1.School of Telecommunication Engineering of Hangzhou Dianzi University,Hangzhou 310018,China
2.State Key Lab of Information Control Technology in Communication System of No.36 Research Institute,China Electronic Technology Corporation,Jiaxing,Zhejiang 314001,China

A robust array beamforming method is proposed,due to the beamforming performance being affected by the coherent interference and angle estimation errors.The weighted spatial smoothing algorithm is used to remove correlation. The constraints on the desired signal are imposed to guarantee the robustness of the algorithm in the certain range of angle estimation errors.The loss of array aperture is avoided by applying full array beamforming transformation.The simulation results show that in coherent interference environment,the pattern of the algorithm has obvious main lobe on desired signal, in favor of receiving the desired signal;the algorithm can maintain higher and flatter Signal to Interference Noise Ratio（SINR）at output in the certain angle estimation errors;as the input Signal to Noise Ratio（SNR）increases,the output SINR of the algorithm increases nearly linearly.

adaptive beamforming;coherent interference;robustness;array aperture

A

TN911.72

10.3778/j.issn.1002-8331.1205-0041

WANG Yang,ZHAO Zhijin,LIU Xiaoli.Robust full array beamforming algorithm.Computer Engineering and Applications,2014,50（6）：205-209.

浙江省青年基金项目（No.Q12F010009）。

汪扬（1990—），男，硕士研究生，主要研究方向：阵列信号处理；赵知劲（1959—），女，博士，教授，博士生导师，主要研究方向：自适应信号处理、认知无线电、压缩感知等；刘晓莉（1984—），女，博士，主要研究方向：阵列信号处理、MIMO雷达参数估计。E-mail：wangyangzhizui@126.com

2012-05-14

2012-06-28

1002-8331（2014）06-0205-05

CNKI网络优先出版：2012-09-07，http://www.cnki.net/kcms/detail/11.2127.TP.20120907.0859.003.html