两级定位-路径问题的变邻域人工蜂群算法

陈久梅，龚英

1.重庆工商大学电子商务及供应链系统重庆市重点实验室，重庆 400067

2.重庆工商大学商务策划学院，重庆 400067

两级定位-路径问题的变邻域人工蜂群算法

陈久梅1，2，龚英1，2

1.重庆工商大学电子商务及供应链系统重庆市重点实验室，重庆 400067

2.重庆工商大学商务策划学院，重庆 400067

建立了两级定位-路径问题的数学模型，提出了一种求解该问题的人工蜂群算法。针对该算法容易出现早熟现象，将近年来国外出现的一种新颖的轨迹式启发式算法——变邻域搜索融入其中，由此提出三种变邻域搜索策略。基于不同变邻域搜索策略的人工蜂群算法和人工鱼群算法的求解效果进行对比仿真。实验结果表明，变邻域人工蜂群算法能有效求解两级定位-路径问题。

两级定位-路径问题；人工蜂群算法；变邻域搜索；物流；配送

1 引言

近年来，物流进城难、成本高、送错货等问题屡见不鲜。为了解决这些问题，提高配送能力，越来越多的企业在城市周边设立中转站，用于进城物品的分拣、拼装和转运。由此形成由“配送中心-中转站-顾客”为节点的两级物流网络。该网络中涉及到的配送中心、中转站的位置、数量，两级网络各节点间的任务分配，以及车辆的调度与配送路径等问题的集成，即两级定位-路径问题（two-Echelon Location-Routing Problem，2E-LRP）[1]。该问题自Jacobsen等[2]提出以来，逐渐成为研究热点。

两级定位-路径问题是一个NP-Hard问题，目前的研究主要集中在启发式求解算法方面。Ambrosino等[3]用大规模邻域搜索算法和重新定位机制求解只有一个配送中心的带异质车队的两级定位-路径问题。Sterle等[4]为设施点有容量限制的两级定位-路径问题建立整数规划模型，使用禁忌搜索算法进行求解。Jin等[5]使用遗传算法和禁忌搜索算法的混合算法求解两级定位-路径问题。Boccia等[6]首先将两级定位-路径问题分解为两个一级定位-路径问题，每个一级定位-路径问题进一步分解为设施定位问题和车辆路径问题，之后使用多阶段迭代嵌入禁忌搜索算法进行求解。王绍仁等[7]针对震后紧急响应阶段应急物流系统优化中的两级定位-路径问题，提出了一种基于两阶段分段思想的“三角”启发式算法进行求解。Nguyen等[8-9]采用贪婪随机自适应搜索、路径重连及学习过程求解两级定位-路径问题。

人工蜂群算法（Artificial Bee Colony，ABC）是由Karaboga[10]于2005年基于蜜蜂觅食原理提出的一种群智能优化算法。它模拟了蜂群依各自分工不同协作采蜜，交换蜜源信息寻找最优蜜源的群体行为。它已被广泛应用于求解旅行商问题、车辆路径问题及设施定位等NP-Hard问题，均取得较好的求解效果。该算法具有良好的求取全局极值能力，并具有对初值、参数选择不敏感、鲁棒性强、简单易实现等优点，但却存在搜索早期过早收敛、搜索后期收敛较慢等问题[10]。近年来，国外出现了一种新颖的轨迹式启发式算法——变邻域搜索（Variable Neighborhood Search，VNS）。该算法的基本思想是在获得局部最优解的基础上，通过系统地改变邻域结构集来拓展搜索范围找到另一个局部最优解。该算法思想简单，容易实现，算法结构与问题无关，适合于各类优化问题，它可被方便地嵌入到其他启发式算法中[11]。在此，针对人工蜂群算法存在的不足，设计嵌入变邻域搜索的人工蜂群算法对两级定位-路径问题进行求解。

2 问题描述及数学建模

2.1 问题描述

两级定位-路径问题是传统定位-路径问题的拓展问题，是两级物流网络中的定位-路径问题，其中涉及到配送中心和中转站两类物流设施的选址、设施与需求点之间的配给以及两级物流网络中车辆的行驶路径。具体可描述如下：由一系列潜在配送中心、潜在中转站及已知顾客所构成的两级物流网络中，物品从配送中心经中转站到达顾客处，在满足设施容量限制、车辆容量限制等约束条件下，确定哪些潜在设施点开放、开放的配送中心应分别为哪些开放的中转站提供物品、开放的中转站应分别为哪些顾客提供物品、两级物流网络中各需多少辆车及每辆车的行驶路线，以实现总成本最小，即两级设施点的开放成本、车辆的使用成本及车辆的运行成本之和最小。该问题的假设条件如下：

（1）两级物流网络中所使用的车辆、两级设施均有容量限制。

（2）每个顾客只能接受来自一个已开放中转站的物品，每个开放的中转站只能接受来自一个已开放配送中心的物品。

（3）二级物流网络中每个顾客只能接受一辆车、一次服务，一级物流网络中每个开放的中转站只能接受一辆车、一次服务。

（4）物品从配送中心出发，必须经过中转站中转才能到达顾客处，不考虑配送中心直接送达顾客的情况，且同级设施之间无货物流动。

（5）物流网络中每辆车仅完成一次旅行，且二级物流网络中车辆从某中转站出发完成行驶路径上所有顾客需求服务后必须回到该中转站，一级物流网络中车辆从某配送中心出发完成行驶路径上所有中转站需求服务后必须回到该配送中心。

（6）车辆行驶成本行驶距离成正比。

2.2 数学建模

2.2.1 符号说明

集合：ND为潜在配送中心集合；NS为潜在中转站集合；NC为顾客集合；E1为一级物流网络边的集合；E2为二级物流网络边的集合；P，R，T⊆ND∪NS∪NC，Z⊆E1∪E2。

参数：QDi为配送中心i的容量；FDi为配送中心i的开放成本；QSi为中转站i的容量；FSi为中转站i的开放成本；QVi为i级物流网络中车辆的容量(i=1，2)；FVi为i级物流网络中车辆的固定使用成本(i=1，2)；cij为边(i，j)上车辆行驶成本；di为顾客i的需求量。

决策变量：uij为一级物流网络中边(i，j)被使用一次为1，否则为0；vij为一级物流网络中边(i，j)被使用两次为1，否则为0；xij为二级物流网络中边(i，j)被使用一次为1，否则为0；yij为二级物流网络中边(i，j)被使用两次为1，否则为0；mij为中转站i分配给顾客j为1，否则为0；nij为配送中心i分配给中转站j为1，否则为0；oi为配送中心i开放为1，否则为0；pi为中转站i开放为1，否则为0。

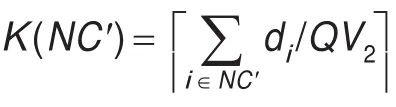
2.2.2 模型建立

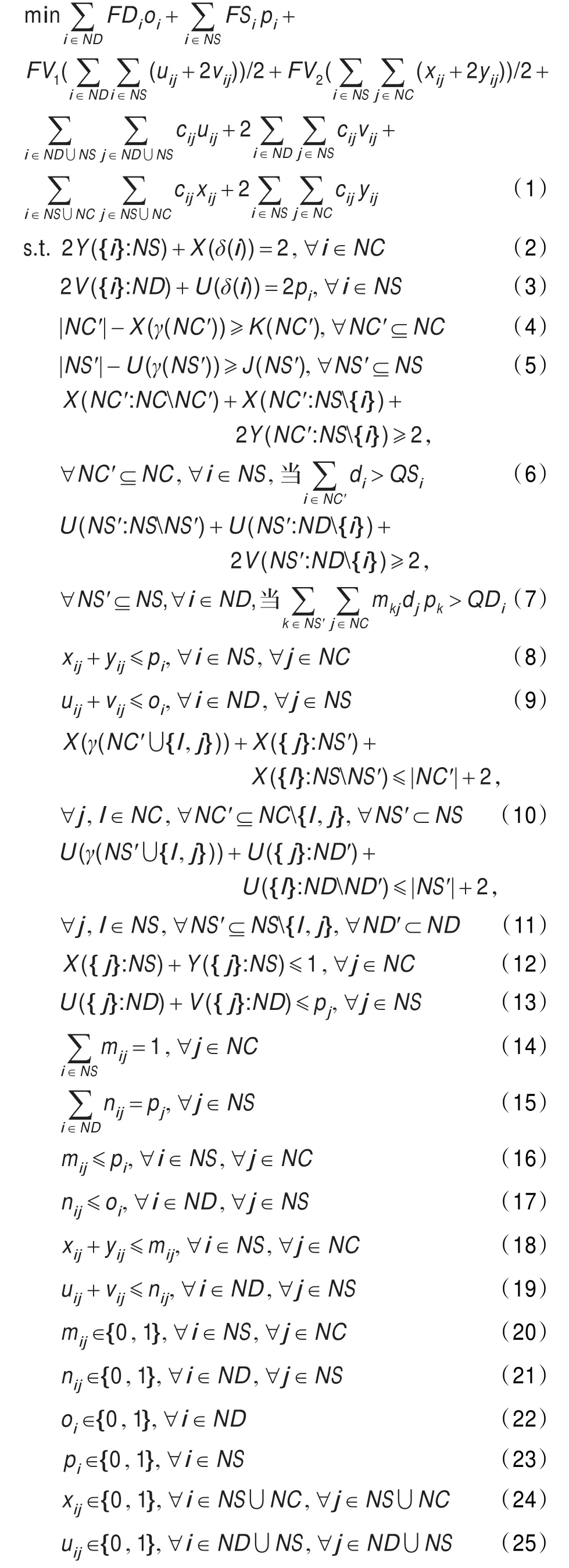
上述模型中，目标函数由八部分组成，其中，第一、二项分别为配送中心和中转站的开放成本，第三、四项分别为一、二级网络中车辆固定使用成本。第五、六项为一级网络中车辆行驶成本，第七、八项为二级网络中车辆行驶成本。

式（2）～（27）为该问题的约束条件，式（2）表示二级物流网络中对任意一个顾客，连接该顾客的边有两条；式（3）表示一级物流网络中如果某中转站开放，那么连接该中转站的边有两条，否则没有边连接该中转站；式（4）表示二级物流网络中车辆运输量不能超过车辆的容量，当K(NC′)=1时，表示子回路消除；式（5）表示一级物流网络中车辆运输量不能超过车辆的容量，当K(NS′)=1时，表示子回路消除；式（6）表示分配给某中转站的顾客需求量之和不超过该中转站的容量；式（7）表示分配给某配送中心的中转站货物量之和不超过该配送中心的容量；式（8）表示二级物流网络中，如果某中转站开放，那么连接该中转站与某顾客的被使用一次和两次的边不能同时存在，否则没有边连接该中转站；式（9）表示一级物流网络中，如果某配送中心开放，那么连接该配送中心与某中转站的用一次和两次的边不能同时存在，否则没有边连接该配送中心；式（10）表示顾客数不小于2的二级物流网络中，从某中转站出发的车辆，完成配送后必须回到该中转站；式（11）表示中转站数不小于2的一级物流网络中，从某配送中心出发的车辆，完成配送后必须回到该配送中心；式（12）表示二级物流网络中对任意顾客，连接该顾客与中转站的被使用一次和两次的边的数量之和小于等于1；式（13）表示一级物流网络中，如果中转站开放，连接该中转站与配送中心的被使用一次和两次的边的数量之和小于等于1，如果中转站不开放，没有边连接；式（14）表示对任意一个顾客，有且仅有一个中转站配给；式（15）表示对任意一个中转站，若开放则有且仅有一个配送中心配给，否则无配送中心配给；式（16）表示如果某中转站分配给某顾客，则该中转站一定开放，如果某中转站未开放，则一定不能分配给任何顾客；式（17）表示如果某配送中心分配给某中转站，则该配送中心一定开放，如果某配送中心未开放，则一定不能分配给任何中转站；式（18）表示若某顾客没有分配给某中转站，则两者之间的边不能被访问，若某顾客分配给某中转站，则连接两者的被使用一次和使用两次的边不能同时存在；式（19）表示若某中转站没有分配给某配送中心，则该两者之间的边不能被访问，若某中转站分配给某配送中心，则连接两者的被使用一次和使用两次的边不能同时存在；式（20）～（27）为决策变量的取值范围。

3 算法设计

人工蜂群算法模拟蜂群的采蜜行为，通过不同角色蜜蜂间的信息交流、角色转换和分工协作来找到问题的最优解。人工蜂群由引领蜂、跟随蜂和侦察蜂组成。引领蜂在蜜源处采蜜并提供所记忆的蜜源信息；跟随蜂以一定的概率选择某个引领蜂去蜜源处采蜜；侦察蜂负责寻找新蜜源。其中蜜源的位置代表优化问题的可行解，蜜源的花蜜含量代表解的质量，称为适应值。

ABC算法工作原理如下：引领蜂寻找蜜源，跟随蜂选择并跟随引领蜂在相应的蜜源位置附近进行邻域搜索，若能搜索到适应值更高的新蜜源，则更新当前蜜源。如果某个蜜源的位置不能在预先设定的循环次数内得到进一步改进，则放弃该蜜源，将其对应的引领蜂转换为侦察蜂。被放弃的蜜源将由侦察蜂找到的新蜜源所取代，此时侦察蜂转换为与新蜜源对应的引领蜂。跟随蜂再次选择引领蜂跟随。如此反复迭代，直到达到结束条件为止。

3.1 算法总体框架

针对两级定位-路径问题，本文在引领蜂及跟随蜂所进行的邻域搜索过程中嵌入变邻域搜索算法，即在邻域搜索过程中系统地改变邻域结构集来拓展搜索范围。具体步骤如下：

步骤1初始化种群参数SN，limit，此时所有蜜蜂为侦察蜂。

步骤2生成SN个初始解，按目标函数值从小到大排序，前一半的解设为当前解，此时一半侦察蜂转换为引领蜂并各自携带一个当前解，一半侦察蜂转换为跟随蜂。

步骤3计算每个引领蜂携带解被选择的概率Pi，引领蜂根据Pi招募跟随蜂。

步骤4每一只引领蜂及其跟随蜂对其携带的当前解进行变邻域搜索，若搜索到比当前解更优的解，则替换当前解；否则，继续进行变邻域搜索，直到达到一定次数limit，若此时仍然未搜索到更优解，则该引领蜂转换为侦察蜂。

步骤5侦察蜂进行全局搜索得到新解，并用新解替换当前解，此时侦察蜂变为引领蜂。

步骤6当所有引领蜂对其携带当前解进行变邻域搜索后，将种群最优解进行保存；若满足程序终止条件，则程序退出，输出种群最优解，否则转步骤3。

3.2 初始解的生成

在此将两级定位-路径问题分为两级，每级进一步划分为设施定位和车辆路径两个子问题。设施定位问题采用随机最近邻策略求解，车辆路径问题采用经典的C-W节约算法进行求解。具体来说，在由中转站与顾客构成的二级网络中，首先随机选择未开放的中转站并将其开放；之后，从距离最近的r个未归给任何中转站的顾客中随机选择某个顾客，并将其归给该中转站，重复此步，直到所有顾客均已归入某中转站或超过该中转站容量限制为止；若存在未归入任意中转站的顾客，则随机选择未开放的中转站并将其开放；按上述方法将相应顾客逐一归入；重复此步，直到所有顾客均归入某相应中转站为止，从而完成二级网络中设施定位问题的求解。按类似的方法，完成由配送中心与中转站构成的一级网络中设施点定位问题的求解。最后，分别针对开放的配送中心、中转站，根据车辆容量限制，使用C-W算法求解两级网络中的车辆路径问题。

3.3 邻域解的产生

两级定位-路径问题，其产生邻域解的考虑对象有两级物流网络中的顾客、中转站及路径三类。以顾客为对象的邻域解采用单个顾客位置的移动（记为N1）及两个顾客之间位置的交换（记为N2）两种方式来产生；以路径为对象的邻域解采用常用的2-opt方式（记为N3）产生；以中转站为对象的邻域解采用单个中转站开放与否的状态改变（记为N4）及两个状态不同的中转站之间进行状态交换（记为N5）两种方式产生。

据此提出三种变邻域搜索策略：

变邻域搜索策略1（记为S1），顺序执行各邻域搜索，若出现比当前解更优的邻域解，则回到N1继续执行，一旦出现比该邻域解更差的邻域解，则继续执行下一步，否则，回到N1继续执行；否则，继续执行下一步，直到结束。

变邻域搜索策略2（记为S2），顺序执行各邻域搜索，若出现比当前解更优的邻域解，则继续用该邻域搜索模块进行搜索，直到比该邻域解更差的解出现，否则，继续执行下一步，直到结束。

变邻域搜索策略3（记为S3），顺序执行各邻域搜索，若出现比当前解更优的邻域解，则结束；否则，继续执行下一步，直到结束。

3.4 选择概率的确定

在此采用人工蜂群算法常用选择概率计算方法，即锦标赛选择策略。锦标赛选择策略是基于局部竞争机制的选择过程，即在种群中随机选择q个个体（竞赛规模）进行比较，适应度值大的被选中，并对其加权值1；如当q=2时，将种群中个体两两比较，并给适应度值好的个体加权值1，对所有个体重复这一操作过程。根据个体权值，由此计算选择概率：

其中，ai为个体i的权值。

该选择策略中选择概率的计算只涉及个体适应度值之间的大小关系，不涉及适应度值的具体取值，能较好避免陷入早熟。

4 算例分析

为分析变邻域人工蜂群算法求解两级定位-路径问题的性能，需用算例进行仿真测试。由于该问题目前缺乏公认的国际算例，本文在文献[12]一级定位-路径问题算例25点、50点、75点基础上，选择前面部分设施点作为两级定位-路径问题的潜在配送中心、剩余设施点作为潜在中转站、顾客点不变产生两级定位-路径问题的算例（算例中各类节点依次编号）。算例需补充和调整的参数如表1所示，其余参数详见文献[12]。

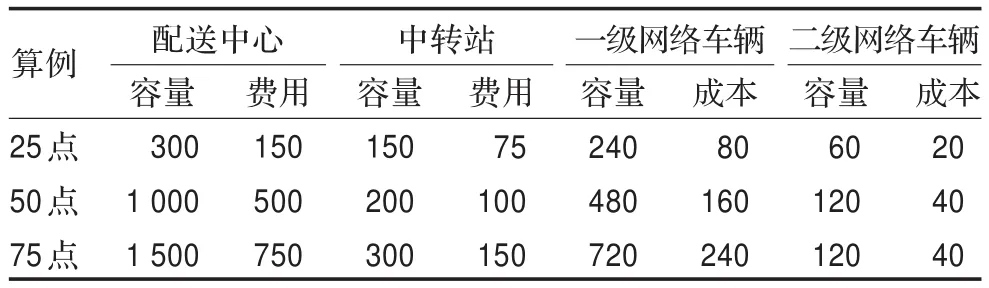
表1 补充、调整的参数

在此使用C sharp编程实现不同变邻域搜索策略下的人工蜂群算法，在Windows XP系统，Pentium®Dual-Core CPU E5700@3.00 GHz、2.00 GB内存的计算环境下，对上述三组不同规模大小的算例进行求解。种群规模SN=50，算法最大迭代次数Tmax=600，邻域搜索最大迭代次数limit=5，初始解生成过程中所用参数r=4，车辆行驶成本与其行驶距离的比例系数取1。

4.1 采用不同变邻域搜索求解效果比较

在此分别采用不同变邻域搜索策略的人工蜂群算法求解两级定位-路径问题的上述算例。随机运行50次的求解结果见表2所示。

由表2可知，采用邻域搜索策略S1求解时，取得的最好解和平均解较优；采用邻域搜索策略S2求解时，取得的最差解较优；采用邻域搜索策略S3求解时，平均计算时间较短。

以下给出分别采用S1、S2、S3三种变邻域搜索策略的人工蜂群算法求解算例“1-4-20”，随机运行50次种群最好解随迭代次数变化趋势图，见图1所示。

从图1可知，采用变邻域搜索策略S1、S2、S3求解时均能较好避免早熟，随着迭代次数的增加，目标函数值不断下降，算法具有较好的收敛性。

4.2 不同算法的求解效果比较

为了进一步了解变邻域人工蜂群算法求解两级定位-路径问题的求解效果，在此采用人工鱼群算法进行对比。借鉴文献[13]的研究成果，将人工鱼群算法的参数设置如下：最大试探次数try-number=5，拥挤度因子σ=0.4，可视范围visual=(Ymax-Ymin)/4，其中Ymax、Ymin为当代种群最好解、最差解对应的目标函数值。人工鱼群算法的运行环境与上述相同。随机运行50次，两种算法求解结果见表3所示。

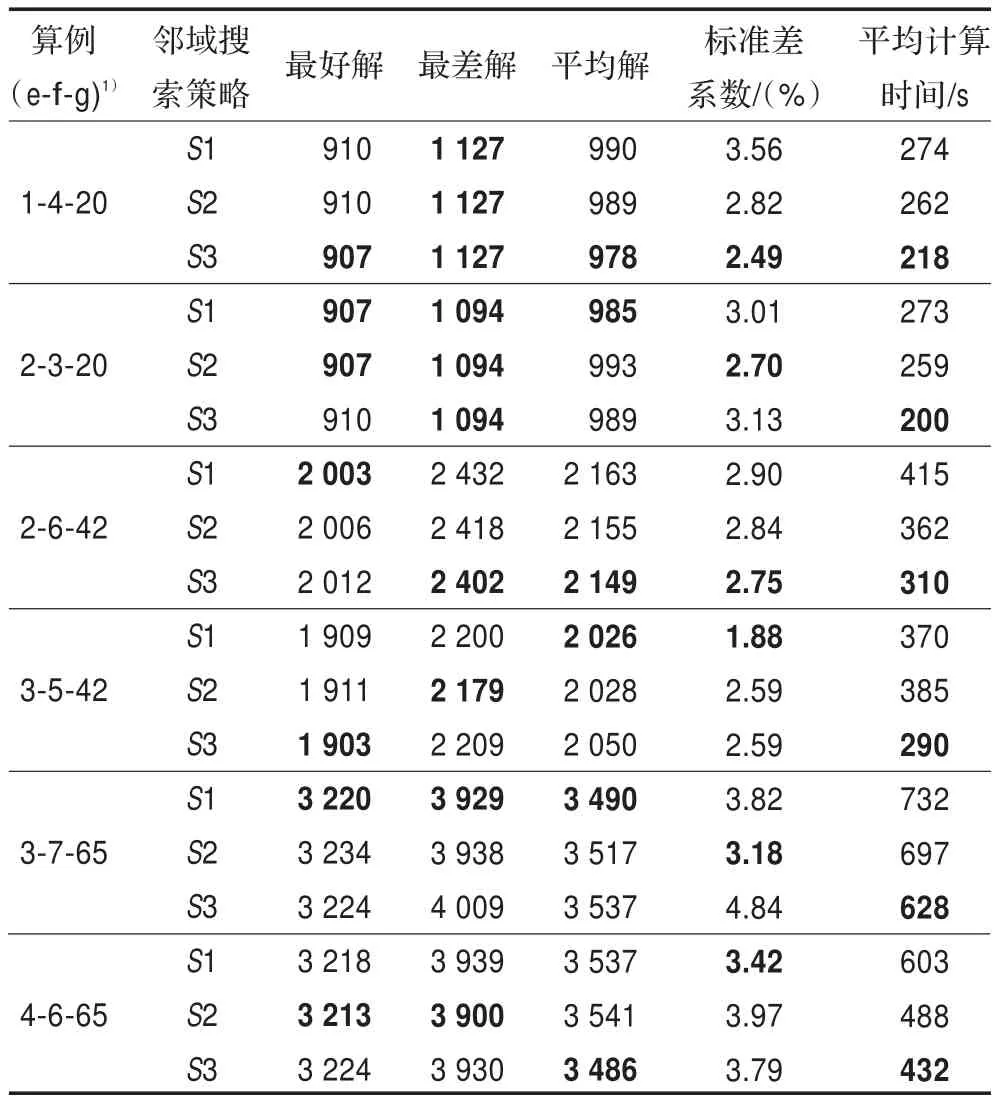
表2 不同邻域搜索策略求解效果比较

图1 种群最好解随迭代次数的变化趋势

由表3可知，人工鱼群算法在最差解及平均解方面较优，变邻域人工蜂群算法在最好解及平均计算时间方面较优。

4.3 算例最好解网络结构

在此，给出算例“3-7-65”最好解“3 220”对应的网络结构图，见图2所示。

从图2可知，潜在的3个配送中心中开放了编号为“1”的1个配送中心，潜在的7个中转站中开放了编号为“1”、“2”、“3”和“7”的4个中转站，从配送中心出发到达各中转站的路径数为2，从各中转站出发到达各顾客点的路径数为12。根据该算例的相关数据，可验证该最好解满足假设条件（1）、（2）、（3）、（4）。由假设条件（5）可知，一级网络车辆数即为2，二级网络车辆数即为12。根据网络中各节点的坐标，采用欧几里德距离计算点与点之间的距离，求和取整得到各条路径的长度，根据假设条件（6）可计算出各条路径车辆行驶成本910（限于篇幅，详细计算过程在此从略）。由此，可计算目标函数=配送中心开放成本750×1+中转站开放成本150×4+一级网络车辆使用成本为240×2+二级网络车辆使用成本40×12+两级网络中车辆行驶成本910=3 220。进一步分析，由文献[12]可计算出该算例的顾客需求量为1 168，结合表1所示参数可知，该最好解开放了最少数量的配送中心、最少的数量中转站，使用了最小数量的车辆。因此，该解的质量较好。

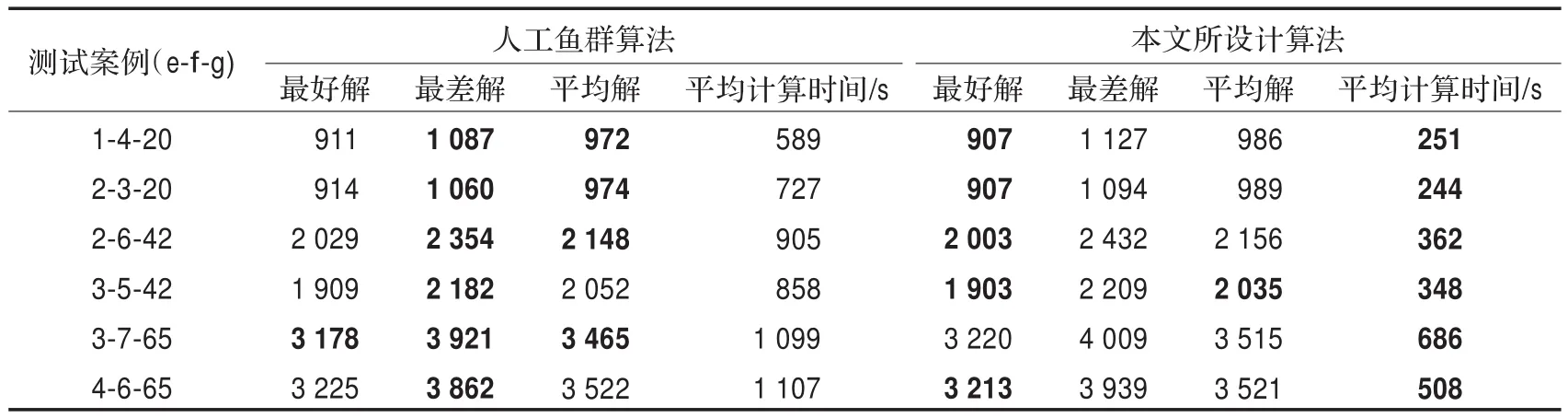
表3 不同算法求解效果比较1）

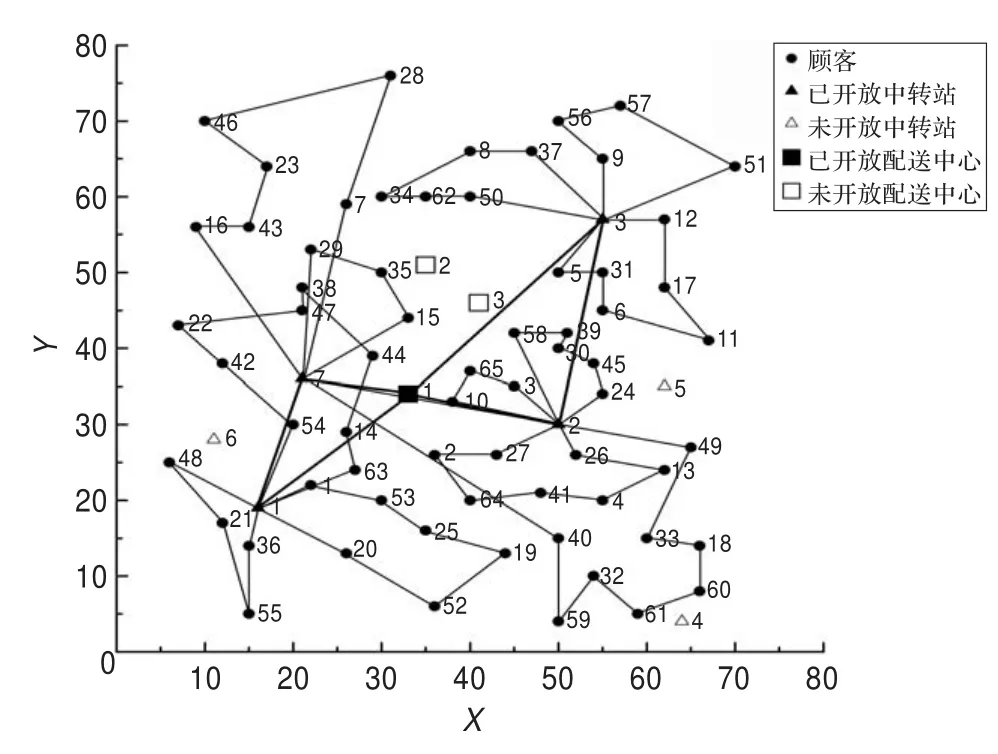
图2 算例“3-7-65”最好解“3 220”的网络结构

5 结束语

针对城市物流配送中的两级定位-路径问题，建立了相应的数学模型，并将求解NP-hard问题效果较好的人工蜂群算法应用于包括多个NP-hard子问题的两级定位-路径问题的求解；针对人工蜂群算法容易出现早熟的问题，在算法的邻域搜索阶段，根据变邻域搜索思想提出了三种变邻域搜索策略。仿真实验结果表明，变邻域人工蜂群算法能有效求解两级定位-路径问题；提出的三种变邻域搜索策略各有优势，可根据实际应用的需要及决策者的个人偏好，选择相应的搜索策略。因此，实际应用时，可根据决策者的风险偏好进行选择。若决策者为风险回避者，应选择基于变邻域搜索策略S2的人工蜂群算法进行求解，以期得到更优的最差解；若决策者为风险中立者或风险追求者，应选择基于变邻域搜索策略S1的人工蜂群算法进行求解，以期得到更优的平均解或最好解。此外，若在某些更关心决策效率的应用情形，如应急物流等，则应选择基于变邻域搜索策略S3的人工蜂群算法进行求解，以期在更短时间内求得满意解。

[1]NagyG，Salhi S.Location-routing：issues，models and methods[J].European Journal of Operational Research，2007，177（2）：649-672.

[2]Jacobsen S K，Madsen O B G.A comparative study of heuristics for a two-level routing-location problem[J].European Journal of Operational Research，1980，5（6）：378-387.

[3]Ambrosino D，Sciomachena A，Scutellàb M G.A heuristic based on multi-exchange techniques for a regional fleet assignment location-routing problem[J].Computers&Operations Research，2009，36（2）：442-460.

[4]Sterle C.Location-routing models and methods for freight distribution and infomobility in city logistics[D].Universita Degli Studi di Napoli“Federico II”，Naples，Italy，2010.

[5]Li Jin，Zhu Y，Shen H，et al.A hybrid genetic algorithm for two-layer location-routing problem[C]//4th International Conference on New Trends in Information Science and Service Science（NISS），2010：642-645.

[6]Boccia M，Crainic T G，Sforza A，et al.A metaheuristic for a two Echelon Location-Routing Problem[C]//Lecture Notes in Computer Science.Berlin Heidelberg：Springer-Verlag，2010：288-301.

[7]王绍仁，马祖军.震害紧急响应阶段应急物流系统中的LRP[J].系统工程理论与实践，2011，31（8）：1497-1507.

[8]Nguyen V P，Prins C，Prodhon C.Solving the two-echelon location routing problem by a GRASP reinforced by a learning process and path relinking[J].European Journal of Operational Research，2012，216（1）：113-126.

[9]Nguyen V P，Prins C，Prodhon C.A multi-start iterated local search with tabu list and path relinking for the two echelon location-routing problem[J].Engineering Applications of Artificial Intelligence，2012，25（1）：56-71.

[10]Karaboga D.An idea based on honey bee swarm for numerical optimization，TR06[R].Kaayseri：Erciyes University，2005.

[11]暴励.人工蜂群算法的混合策略研究[D].太原：太原科技大学，2010.

[12]胡大伟.设施定位和车辆路线问题模型及其启发式算法研究[D].西安：长安大学，2008：129-133.

[13]李晓磊.一种新型的智能优化方法——人工鱼群算法[D].杭州：浙江大学，2003.

[14]董伟.变邻域搜索算法研究及在组合优化中的应用[D].阜新：辽宁工程技术大学，2011：1-2.

CHEN Jiumei1，2,GONG Ying1，2

1.Chongqing Key Laboratory of Electronic Commerce&Supply Chain System,Chongqing Technology and Business University,Chongqing 400067,China
2.Strategical Planning Department,Chongqing Technology and Business University,Chongqing 400067,China

A mathematical model of two-echelon location-routing problem is established.Artificial Bee Colony algorithm is put forward to solve this problem.Since this algorithm usually has premature convergence.Variable neighborhood search, a novel path heuristic algorithm appearing abroad in recent years,is blended in this algorithm.At the same time,three kinds of variable neighborhood search strategy are put forward.The comparison simulation between Artificial Bee Colony algorithm with different variable neighborhood search strategies and artificial fish swarm algorithm has been done.The experimental results show that Artificial Bee Colony algorithm with variable neighborhood search can effectively solve two-echelon location-routing problem.

two-Echelon Location-Routing Problem（2E-LRP）;Artificial Bee Colony（ABC）algorithm;Variable Neighborhood Search（VNS）;logistics;distribution

A

F224.3

10.3778/j.issn.1002-8331.1309-0335

CHEN Jiumei,GONG Ying.Artificial Bee Colony algorithm with variable neighborhood search for two-Echelon Location-Routing Problem.Computer Engineering and Applications,2014,50（6）：25-30.

国家自然科学基金（No.71101159）。

陈久梅（1976—），女，博士，副教授，研究领域为物流系统优化、智能算法等；龚英（1968—），女，教授，研究领域为物流与供应链。E-mail：chenjiumei@163.com

2013-09-23

2013-11-10

1002-8331（2014）06-0025-06

CNKI网络优先出版：2013-11-15，http://www.cnki.net/kcms/detail/11.2127.TP.20131115.1121.009.html