通用几何约束系统统一建模研究

石志良，陈谊，张忠全

武汉理工大学机电工程学院，武汉 430070

通用几何约束系统统一建模研究

石志良，陈谊，张忠全

武汉理工大学机电工程学院，武汉 430070

在几何约束和几何实体的基本约束和欧拉参数表达的基础上，研究了通用几何约束系统的统一建模问题。通过对三维几何实体姿态约束和位置约束解耦性的分析，抽象出球实体、盒体和球盒体三种基本几何实体表达空间几何实体，并以基本约束的组合表达几何约束，形成几何约束模型特有的层次结构；并以有向图管理几何约束系统，可以清晰地反映姿态约束和位置约束的解耦性，实现约束系统的细粒度分解，得到规模更小的求解序列，实现高效求解。方法实现于原型系统WhutVAS中。

几何约束；几何约束求解；约束处理；图分解；欧拉参数

1 引言

在几何约束系统中，几何实体之间的约束关系是非常复杂的，如何建立有效的几何约束系统模型，是几何约束系统研究的基础。理想的几何约束系统应该做到表达、维护和求解的一致性，几何空间的可拓展性及几何上的可解释性。在几何约束系统的研究中，基于变量几何[1-3]的几何约束系统建模方法，以几何实体特征点的参数变量来表达几何实体，以参数变量之间的约束方程来表达几何约束，其局限性是显而易见的。这种采用整体笛卡尔坐标建立系统约束和约束方程的方法虽然从理论上来说可以进行任何类型的约束求解，但它需要建立一个较大的方程组，对于几何约束的表达和求解都很不方便。基于几何实体和图论[4-9]对几何约束系统进行建模，可以直接管理二、三维空间中的几何实体及其关联的几何约束，具备较好的几何空间可拓展性及几何上的可解释性，但是，由于几何约束的多样性，导致几何约束的表达复杂，简洁性不够，而且装配约束的约束度通常大于1，不利于冗余约束的判定。为了解决这些问题，需要研究基础共性的表达问题，彭小波[10]以运动学和动力学的研究为基础，提出采用欧拉参数和基本约束[11]表达几何实体和几何约束，结合有向图，在几何建模的层次上将二、三维几何约束问题以及多刚体系统动力学问题统一起来，并扩展到多刚体系统的分析计算领域，该方法以少量的基本几何约束表达所有的几何约束，模型的抽象和简洁性好，然而，却忽视了欧拉参数表达的几何实体参数结构上具有一定的可解耦性，对几何实体的统一表达没有作进一步的研究和抽象，有向图顶点仍然是通常的几何实体，从而导致求解的规模较大。文献[12]研究了三维实体之间的重合、角度和距离约束的统一几何表达。本文以欧拉参数表达的几何实体的姿态和位置约束的解耦性研究为基础，抽象出球实体、盒体和球盒体三种基本几何实体表达空间几何实体，并采用基本约束的组合表达几何约束，在有向图上清晰地表达几何约束系统的本质特征，基于有向图的几何约束优化匹配算法[13]，为二、三维几何约束求解提供了内在的统一机理，具有很强的理论意义。

2 基于欧拉参数的几何实体和几何约束的表达

几何实体的方位由姿态和位置确定，姿态表示几何实体在空间中的方向，如平面的法向量，直线的方向，刚性体的方向余弦矩阵，可以由附着在几何实体上的局部坐标系的姿态表达；位置由附着在几何实体上的局部坐标系的位置表达，Haug[11]采用欧拉参数表达几何实体的方位，以基本约束dot1、dot2、等X、等Y、等Z和距离条件[10]表达装配约束。由于三维空间复杂于二维空间，二维空间的欧拉参数表达可以看作是三维空间的特例，因而，本文仅给出三维常见装配约束的基本约束表达，如表1所示。

表1 常用装配约束及其位置基本约束表达1）

以共轴约束为例，共轴约束限制4个自由度，如图1 （a）所示，假定P1和P2分别是轴线L1和L2的基点，h1，h2分别是轴线L1，L2的方向矢量，矢量f1，g1，h1正交，假定轴线L1固定，要使L1和L2共轴，需要满足f1⊥h2，g1⊥h2，f1⊥d12和g1⊥d12，f1⊥h2和g1⊥h2决定圆柱体2的姿态，f1⊥d12和g1⊥d12决定圆柱体2的位置，对应的约束方程如图1（b）。

图1 圆柱体共轴约束实例图

3 几何实体姿态和位置的解耦性质

几何实体的姿态和位置具有一定的可解耦性质，有利于求解。因为从几何上来说，存在这样一个事实：移动几何实体不破坏几何实体的姿态，而转动几何实体时却可以破坏几何实体的位置例如，共轴约束含有4个约束分量，约束度是4，在可解耦的情况下，共轴约束的4个约束分量可以分为轴平行的2个姿态约束和点在轴线上的2个位置约束，求解时可以先根据姿态约束确定姿态，然后在确定的姿态下，求解位置约束，反之则不能够求解。当然，也可以采用整体数值求解，需要联立4个方程，效率显然较低。假设以代表基本约束dot1，代表基本约束dot2是指其他的距离约束关系，存在如下性质：

性质1假设刚性体RB参数匹配的约束满足条件

姿态约束和位置约束是可以解耦求解的。刚性体存在三个约束，表明姿态是完整约束的，则不论刚性体是完整约束还是欠约束，一定是可解耦求解的，如3A 3D、3A 2D和3A 1D构型[13]。

性质2如果与刚性体RB参数匹配的和约束满足条件

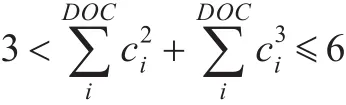
则姿态约束和位置约束一定不可解耦求解。

由于刚性体存在三个移动自由度，如果匹配的和约束数大于3，那么需要通过转动来满足约束，使得姿态和位置约束求解不可解耦。如2A 4D、1A 5D和6D完整约束构型[14]。

如果在可装配的条件下，排除性质1和性质2的情况，处于欠约束情况下的姿态和位置的解耦求解不存在定性，常见的装配约束都是可以解耦的，例如两个刚性体上两个轴线的共轴约束、平行轴相距约束、两个平面的共面约束、面面相距约束等，姿态和位置是可以解耦求解。但是，如果两个刚性体受到一个平行约束和两个距离约束，刚性体初始方位的不同，可能会导致不可解耦求解，需要同时变换刚性体的姿态和位置来满足距离约束。虽然欠约束情况下的姿态和位置的解耦求解不存在定性，但是能够分离出的可解耦情况对几何约束求解是很有意义的。对于欠约束情况下的姿态和位置非定性解耦求解，通常是先求解姿态约束，然后依据位置约束和确定的姿态，判定是否存在解，如果存在，则可解耦，否则不可解耦，采用整体数值求解。

4 几何实体的统一表达

4.1 基本几何实体认定

由几何实体的姿态和位置的解耦性分析，以及姿态约束和位置约束的性质可知，仅匹配几何实体的姿态，和约束可匹配几何实体的姿态和位置，由此可以产生一个很朴素的思想：

几何实体所受的几何约束中，让决定几何实体姿态的基本约束单独求解几何实体的姿态，而决定几何实体位置的基本约束单独求解几何实体的位置，从而将几何实体方位的统一求解分为姿态和位置的独立求解，降低求解的规模。

为了在几何约束图上表达这种关系，需要对几何实体的表达作进一步的研究和抽象，为此，引入球实体、盒体和球盒体三种基本几何实体。球实体是一个只与空间方向相关的抽象实体，由欧拉参数组p=[e0，e1，e2，e3]表达，球实体仅与几何实体的姿态相关，自由度是3；盒体是一个只与空间位置相关的抽象实体，由参数组r=[x，y，z]表达，盒体仅与几何实体的位置相关，自由度是3；球实体和盒体可以表示几何实体的方位，但是，三维空间的球面和圆柱面都存在一个形状自由度，为清晰地表达球面和圆柱面，引入球盒体的概念，球盒体是一个与几何实体的位置和形状参数相关的抽象实体，由参数组r=[x，y，z]和形状参数表达，自由度是4，表2是三种基本几何实体的描述。

表2 三种基本几何实体的描述

4.2 基于基本几何实体的三维几何实体表达

基于基本几何实体，考察三维空间中的点、直线、平面、球面、圆柱面和刚性体，存在如下的表达方式：

（1）点

空间点的边界表示为p(x，y，z)，欧拉参数表示为rp=r+Aps′p，自由度是3，因而以盒体表达。

（2）直线

在三维空间中，设固结在直线上的局部坐标系为o′x′y′z′，直线的位置由局部坐标系原点o′确定，欧拉参数表示为ro=r′+Aos′o；直线的空间姿态由x′y′z′的姿态确定，直线的方向由向量v′表示，欧拉参数表示为v=Avv′，与方向向量正交的向量为h和g，v′、h和g表示局部坐标系o′x′y′z′的姿态，由此可知，直线的姿态可以表示为球实体，直线的位置可以表示为盒体。在三维空间中，直线的自由度是4，球实体和盒体的自由度之和是6，则需要在球实体和盒体之间添加内部约束，以保证直线表达的正确性。取直线上的任意一点rp（不同于原点o′，该点相当于待确定直线上的点），则有rp和o′连线的方向与v′一致的条件成立，由基本约束可知，需添加2个dot2约束

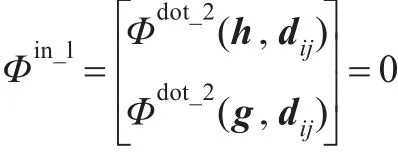
其中dij=rp-ro约束度是2，与三维空间直线的几何意义吻合。

（3）平面

在三维空间中，设固结在平面上的局部坐标系为o′x′y′z′，平面的位置由局部坐标系原点o′确定，欧拉参数表示为ro=r′+Aos′o；平面的空间姿态由x′y′z′的姿态确定，平面的法向由向量v′表示，欧拉参数表示为v=Avv′，与法向量正交的向量为h和g，v′、h和g表示局部坐标系o′x′y′z′的姿态，由此可知，平面的姿态可以表示为球实体，平面的位置可以表示为盒体。在三维空间中，平面的自由度是3，球实体和盒体的自由度之和是6，则需要在球实体和盒体之间添加三个内部约束，以保证平面表达的正确性。取全局坐标原点到平面上的垂足为R，则有R和o′连线的矢量与v′满足垂直约束，由基本约束可知，需添加1个dot2和2个dot1约束：

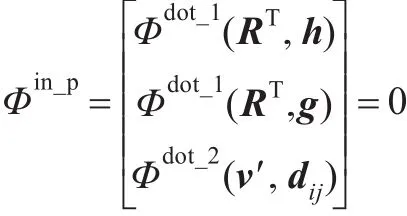
其中dij=R-ro。

（4）球面

在三维空间中，球面的位置由球心的坐标p(x，y，z)确定，由于球面具有空间对称的性质，不具备方向，球面的半径是形状自由度，具有4个自由度，这些性质决定球面可以采用球盒体表达，球面的位置由欧拉参数表示为rp=r+Apsp。

（5）圆柱面

在三维空间中，圆柱面具有4个方位自由度和1个形状自由度，方位自由度由圆柱面的轴线决定，形状自由度表示圆柱面的半径，根据直线的表达可知，圆柱面可以采用球实体和球盒体表达，同样需要对球实体和球盒体添加两个内部dot2约束，约束度为2。

（6）刚性体

三维空间刚性体的自由度是6，3个转动自由度和3个移动自由度，由欧拉参数表达的3个转动自由度由球实体表达，3个移动自由度由球盒体表达，球实体和球盒体之间不存在内部的约束关系。

通过对基本几何约束和基本几何实体的研究可知，装配约束可以由基本约束的组合来表达，几何实体可以由基本几何实体和基本几何约束的组合表达，这使得几何约束模型的表达呈现出其特有的层次结构，如图2所示。

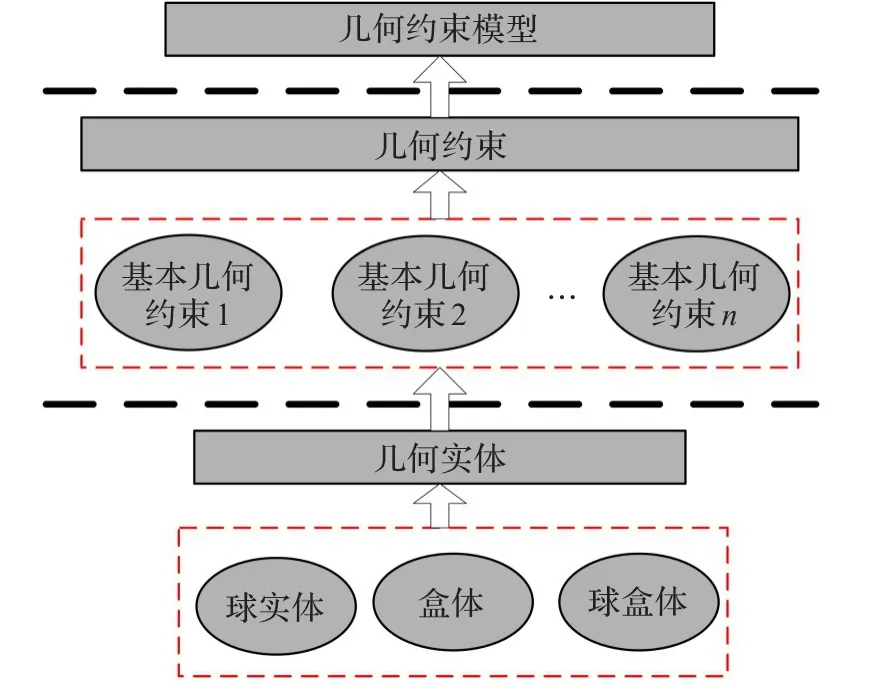
图2 几何约束模型层次结构图

5 几何约束系统建模

基于几何约束模型层次结构，采用有向图G=(V，A)描述几何约束系统，其中V是表达几何约束系统中所有几何实体的顶点集合，以基本几何实体表达几何实体，则V仅由球实体、盒体和球盒体组成的集合。有向弧集合A={a}，一条有向弧表示一个基本约束，具有1个约束度，如果以有向弧直接表示装配约束，而装配约束的约束度通常大于1，则有向弧的权值大于1，导致在有向图上无法清晰地表示冗余约束。

如果与顶点v匹配的约束数m小于其自由度DOF(v)，则称顶点v是自由顶点；如果m等于DOF(v)，则称v是固定顶点。在有向图中，如果顶点v1到v2存在一条路径P，且v1是自由顶点，则称P是从v2到v1的逆向可逆路径，简称可逆路径。路径P所包含的有向弧的条数称为P的长度。如果G为有向无环图，则从顶点v∈V出发的所有路径上的顶点集称为v的传播域，从v出发所有逆向路径上的顶点集称为v的先决域。

构造几何约束有向图G的算法关键在于：在有向图上为新增约束c寻找匹配顶点v，其实质是有向图上的＜c，v＞二部图匹配。简单地说，构造几何约束有向图的过程实际上就是为每条有向弧确定匹配顶点的过程。

构造规则1如果两个相关顶点中有一个顶点为固定顶点，另外一个为自由顶点，则约束与自由顶点匹配。

构造规则2如果不属于同一个强连通分量的两个相关顶点的均为自由顶点，则约束匹配于传播域体积较小的顶点。

构造规则3如果两个相关顶点的剩余自由度都为0，则从两个相关顶点开始，找出一条最短的可逆路径，将这条路径反向，相应顶点的剩余自由度增加，新增约束与之匹配。

以上的三个构造规则是几何约束与顶点匹配的通用规则，在以基本几何实体表达的有向图中，顶点仅由三种基本几何实体组成，添加的装配约束由dot1、dot2和距离等基本几何约束组成，由于基本几何约束的特定的性质，与基本几何实体的匹配具有特殊的特性。

性质3dot1基本几何约束只能够在球实体之间依据构造规则匹配，如果不满足匹配的条件，则该约束冗余。

性质4dot2基本几何约束可以在球实体、盒体和球盒体之间依据构造规则进行匹配；如果待匹配的盒体或球盒体的剩余自由度为0，而该盒体或球盒体对应的球实体是自由顶点，dot2可与球实体匹配，否则，依据构造规则进行匹配。

性质5距离约束在盒体或球盒体之间依据构造规则进行匹配，如果待匹配的盒体或球盒体的剩余自由度为0，而该盒体或球盒体对应的球实体是自由顶点，距离可与球实体匹配，否则，依据构造规则进行匹配。

欠约束情形下的匹配多样性会产生不良的强连通分量，增加求解时间花费。为此采用优化处理方法，文献[13]对此作了详细的阐述，最终得到一个强连通分量体积较优的求解序列。在求解序列中，对于每个几何实体对应的基本几何实体，如果是可解藕的，则先求解姿态和位置约束，然后求解内部约束。

6 实例分析

为验证本文方法的正确性，采用一个回转窑托轮轴装配的实例进行验证。图3（a）为托轮轴装配模型，其中装配部件有中心轴1、托轮2、内挡圈3、轴承4、套筒5、轴承6和外挡圈7，爆炸图如图3（b）所示；装配约束有共轴约束CoLL(1，2)、CoLL(1，3)、CoLL(1，4)、CoLL(1，5)、CoLL(5，6) 和CoLL(6，7)，共面约束有CoFF(1，2)、CoFF(1，3)，CoFF(3，4)、CoFF(4，5)、CoFF(5，6)和CoFF(6，7)。由于装配部件为空间刚体，采用球体Si和盒体Bi分别表示部件i的姿态参数和位置参数，以分别表示部件i的转动和移动，球体Si和盒体Bi分别具有3个转动自由度和3个移动自由度。假设中心轴1的位姿固定，采用基本约束分量表达装配约束，在剔除冗余约束分量后，可得到如图3（c）所示的约束有向图。该约束有向图可采用并行求解，其求解序列如图3（d）所示为{Sq0，Sq1，Sq2，Sq3，Sq4，Sq5，Sq6，Sq7，Sq8，Sq9}，其中Sq1和Sq5内的顶点可并行求解。

图3 托轮轴装配模型及其约束图

7 结论

本文借鉴多体系统分析中的欧拉参数方法，以几何实体和几何约束的欧拉参数表达为基础，通过对欧拉参数表达姿态约束和位置约束的解耦性分析，抽象出球实体、盒体和球盒体三种三维空间的基本几何实体，并以球实体、盒体和球盒体对三维空间中的点、直线、平面、球面、圆柱面和刚性体进行统一表达，以简洁的基本几何实体和基本几何约束，结合有向图对几何约束系统进行建模，描述了几何约束求解的本质特征，可以清晰地表达姿态约束和位置约束的解耦性；本文的方法解决了二维与三维的几何实体和几何约束统一模型问题，为二、三维几何约束求解提供了内在的统一机理，具有很强的理论意义，同时，为后续对姿态约束和位置约束分别采用解析求解，进一步提高求解效率奠定了基础。但本文的表达模型适用于三维空间中的点、直线、平面、球面、圆柱面和刚性体之间的装配关系，是否适用于除圆柱和球以外的二次曲面的表达需要做进一步的研究和完善。

[1]Lin V C，Gossard D C，Light R A.Variational geometry in computer-aided design[J].Compute Graphics，1981，15（3）：171-177.

[2]Serrano D，Gossard D.Constraint management in conceptual design[J].A rtificial Intelligence in Engineering Design，Computational Mechanics Publications，1988.

[3]A it-Aoudia S，Jegou R，Michelucci D.Reduction of constraint systems[C]//Combined Proceedings of EDUGRAPHICS’93 and COMPUGRAPHICS’93，1993：31-40.

[4]Owen J C.Algebraic solution for geometry from dimensional constraints[C]//Proceedings of ACM Symposium on Solid Modeling Foundation，Austin，TX，1991：397-407.

[5]K ramer G.Solving geometric constraints systems：a case study in kinematics[M].Cambridge，MA：M IT Press，1992.

[6]Hoffmann C M，Lomonosov A，Sitharam M.Decomposition plans for geometric constraint systems II new algorithms[J]. Journal of Symbolic Computation，2001，31（4）：408-428.

[7]Gao X S，Lin Q，Zhang G.A C-tree decomposition algorithm for 2D and 3D geometric constraint solving[J].Computer-Aided Design，2006，38（1）：1-13.

[8]董金祥，葛建新，高屹，等.变参绘图系统中约束求解的新思路[J].计算机辅助设计与图形学学报，1997，9（6）：513-519.

[9]李彦涛，胡事民，孙家广.一个几何约束系统分解的新算法[J].计算机辅助设计与图形学学报，2000，12（12）：926-930.

[10]彭小波.二、三维几何约束统一求解器原理与方法研究[D].武汉：华中科技大学，2002.

[11]Haug E J.机械系统的计算机辅助运动学和动力学[M].刘兴祥，译.北京：高等教育出版社，1996.

[12]Haller K，John A L，Sitharam M，et al.Body-and-cad geometric constraint system s[J].Computational Geometry：Theory and Applications，2012，45（8）：385-405.

[14]Gao X S，Lei D L，Liao Q Z，et al.Generalized Stewart-Gough platforms and their direct kinematics[J].IEEE Trans on Robotics，2005，21（2）：141-151.

[13]陈立平，王波兴，彭小波.一种面向欠约束几何系统求解的二部图匹配优化处理方法[J].计算机学报，2000，23（5）：523-530.

SHI Zhiliang,CHEN Yi,ZHANG Zhongquan

School of M echanical and Electronic Engineering,Wuhan University of Technology,Wuhan 430070,China

A united modeling method of generalized geometric constraint system is investigated on the basis of expressing geometric constraints and geometric elements by basic geometric constraints and Euler parameter,respectively.After analyzing the decoupled property of orientation and position constraints related with spatial geometric elements,the basic bodies are summarized into ball,box and ball-box body to express spatial geometric elements,together with assembly constraints expressed by a combination of basic constraints,which forms a particular hierarchy structure of geometric constraint model.The geometric constraint system is coded as a directed geometric constraint graph which describes the relation among the basic geometric elements.The model method can reflect the decoupled property of orientation and position constraints clearly.The smaller solving units and the efficient solving sequence can be obtained.This method has been implemented in prototype system WhutVAS.

geometric constraint;geometric constraint solving;constraint handling;graph decomposition;Euler parameter

A

TP391

10.3778/j.issn.1002-8331.1209-0191

SH I Zhiliang,CHEN Yi,ZHANG Zhongquan.Research on united modeling method of generalized geometric constraint system.Computer Engineering and Applications,2014,50（16）：159-163.

国家自然科学基金（No.50905132）。

石志良（1974—），男，博士，副教授，主要研究方向为约束求解、参数化设计及智能CAD系统；陈谊（1988—），男，硕士研究生，主要研究方向为数字化设计。E-mail：shizhil998@yahoo.com.cn

2012-09-19

2013-01-05

1002-8331（2014）16-0159-05

CNKI网络优先出版：2013-01-18,http://www.cnki.net/kcms/detail/11.2127.TP.20130118.1024.010.htm l