欧拉方程的隐式间断有限元算法研究
2014-07-07段治健
段治健
1.咸阳师范学院数学与信息科学学院,陕西咸阳 712000
2.西北工业大学翼型叶栅空气动力学国防科技重点实验室,西安 710072
欧拉方程的隐式间断有限元算法研究
段治健1,2
1.咸阳师范学院数学与信息科学学院,陕西咸阳 712000
2.西北工业大学翼型叶栅空气动力学国防科技重点实验室,西安 710072
针对Euler方程,设计了适合间断Galerkin有限元方法的LU-SGS、GMRES以及修正LU-SGS隐式算法。采用Roe通量以及Van A lbada限制器技术实现了经典LU-SGS、GMRES算法,引入高阶项误差补偿,发展了修正LU-SGS算法。以NACA 0012、RAE2822翼型为例验证分析了算法的可靠性和高效性。结果表明修正LU-SGS算法存储量较少,程序实现方便,而且计算效率是LU-SGS算法的2.5倍以上,接近于循环GMRES算法。
间断有限元方法;LU-SGS算法;GMRES算法;限制器
1 引言
近年来,间断有限元方法(Discontinuous Galerkin FEM,DGM)[1]在解决含有间断现象的问题中发挥着越来越大的作用,由于DGM保持了有限元法和有限差分法的优点,可以处理复杂区域边界、复杂边界条件,易于实现自适应计算;可以得到任意阶精度的格式;容易实现并行计算;具有良好的稳定性和间断捕捉能力,所以被广泛应用于水动力学、气动力学、波传播等问题[1-4]。尽管DGM具有高精度、收敛快的优点,但对大型问题而言计算效率是一个瓶颈,然而隐式算法是提高计算效率最重要的途径。鉴于隐式格式的高效率和较好的稳定性,以及近年来非结构网格技术的蓬勃发展,许多高性能的隐式算法在计算空气动力学领域中脱颖而出。隐式时间推进格式往往都是无条件稳定的,相对于显式格式,时间步长约束小、总体计算时间短。著名的隐式方法有:ADI方法、LU-SGS方法[5]、GMRES方法[6]等,并得到了进一步发展[7-8]。相比之下,LU-SGS格式占用内存低,计算量小,每步时间推进只需要从前到后、从后到前扫描计算即可。
本文研究了LU-SGS、GMRES、修正LU-SGS隐式时间推进格式,针对NACA 0012、RAE2822翼型比较了三种算法的优劣性,发展了一套高效的双曲守恒律隐式间断有限元方法。
2 间断有限元方法
不考虑体积力和外部热源,笛卡尔坐标系下的Euler方程形式如下:

其中,U为守恒变量,Fj为对应无粘通量,ρ,e,p分别为气体的密度、单位体积总内能及压强。ui是xi方向的速度,δij是K ronecker函数。考虑到理想气体的热力学特性,状态方程如下:

取γ=1.4为比热比。
在式(1)两边乘以测试函数W,在计算域内运用分部积分公式,得到弱形式:

这里Γ是Ω的边界,nj是边界外法向量。
在计算域划分网格上,用近似解Uh,Wh代替解析解U,W,每个单元内:

因为间断有限元方法在区域边界不要求连续,这样数值通量处理方法与有限体积方法相同,如Godunov、Engquist-Osher、HLL/HLLC、LF、LLF、Roe数值通量等。本文采用Van A lbada限制器[9],数值通量采用Roe格式,该格式相对简单,实际计算会更加方便,数值效果良好。
3 GMRES方法
具有平方敛速的共轭梯度法[10]是New ton迭代隐式算法的一种,GMRES算法属于其中一种,因而倍受关注,循环GMRES算法相对于GMRES算法收敛性通常差一些,但是存储量相对较少。因此本文采用循环GMRES算法。对于给定的非对称线性方程组Ax=f,循环GMRES算法如下:
给定K rylov子空间:Km=Span{r0,A r0,…,Am-1r0},而Lm=A Km=Span{A r0,A2r0,…,Amr0},给定误差ε。
(1)选择初始解x0∈Rn,计算残差r0=f-Ax0。

4 LU-SGS方法
当式(4)中取为常数时,则方程变为:

其中,Vi为网格单元i的体积,Δt为时间步长,为第n+1层上的残值,Fij为单元i和单元j的公共网格面上的无粘通量,n为网格面的外法线单位矢量,ΔS为网格面的面积。将式(5)泰勒展开,线化为:

从而得到一个N维的线性方程组(N为网格总数):

将系数矩阵分解为A=D+L+U,式(7)变为:
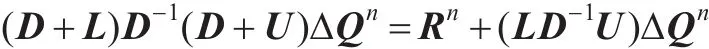
其中,D为对角矩阵,U,L为严格上、下三角矩阵。忽略高阶小量(LD-1U)ΔQn,方程只需两次扫描便可完成求解。忽略了高阶小量虽不会影响精度,但增加了截断误差会影响收敛速度,所以可以将高阶小量进行补偿。具体计算过程如下:


上式计算过程同(1)、(2)。
5 数值算例及结果分析
算例1 NACA 0012翼型跨音速无粘绕流,计算网格节点2 270个,单元数为4 355个。计算状态为Ma=0.8,α=1.25°。
算例2 RAE2822翼型跨音速无粘绕流,计算网格节点2 270个,单元数为4 355个。计算状态为Ma=0.725,α=2.54°。
图1和图2分别为NACA 0012和RAE2822翼型的压力系数分布曲线,数值计算的结果与实验值基本吻合。

图1 NACA 0012翼型表面压力系数对比

图2 RAE2822翼型表面压力系数对比
图3和图4分别为两个算例时间收敛曲线。可以看出,循环GMRES算法计算效率远高于LU-SGS格式。计算效率是LU-SGS格式的3倍左右。修正LU-SGS格式效率接近于循环GMRES算法,且所需存储量较少,单步迭代时间短,计算效率是LU-SGS格式的2.5倍以上。

图3 NACA 0012翼型计算时间曲线

图4 RAE2822翼型计算时间曲线

图5 NACA 0012翼型随CFL数变化计算时间曲线
图5和图6中明显可以看出,克服了显式方法严格的条件限制,CFL数从1变到10时,残值与时间效率提高了近2倍,从100到1 000时,几乎吻合,此时CFL数对于计算效率的影响几乎为0。总体来说,LU-SGS格式的单步计算量最少,收敛迭代步数最多。循环GMRES格式单步计算时间最长,收敛所需的步数最少。修正LU-SGS格式计算效率接近循环GMRES格式,且所需存储量少。

图6 NACA 0012翼型随CFL数变化迭代步数收敛曲线
6 结束语
本文研究了欧拉方程的三种隐式间断有限元算法,显然GMRES格式效率最高,但是其算法复杂,编程实现比较困难,而且对内存的需求较大。修正LU-SGS格式明显优于传统LU-SGS格式,计算效率接近于GMRES算法,显示出了其良好的稳定性和求解效率。当然,线性方程组的并行处理技术[11-12],近年来发展的p、hp多重网格方法[13-14],或者系数矩阵条件数较大时,采用ILU(0)、Block-ILU(0)[15]、Gauss-Seidel、SSOR预处理方法等,都可以很好地提高计算效率。
[1]Reed W H,Hill T R.Triangular mesh methods for the Neutron Transport equation,LA-UR-73-479[R].Los Alamos Scientific Laboratory,1973.
[2]Cockburn B,Shu C-W.Foreword for the special issue on discontinuous Galerkin method[J].Journal of Scientific Computing,2005:22-23.
[3]Luo H,Beaum J D,Lohner R.On the computation of steadystate compressible flow s using a discontinuous Galerkin method[J].International Journal for Numerical Methods in Engineering,2008,73:597-623.
[4]Qiu J X,Liu T,Khoo B C.Runge-Kutta discontinuous Galerkin methods for compressible two-medium flow simulations:One-dimensional case[J].Journal of Computational Physics,2007,222:353-373.
[5]Yoon S,Jameson A.Lower-upper symmetric Gauss-Seidel method for the Euler and Navier-Stoker equations[J]. AIAA Journal,1988,26(9):1025-1026.
[6]Saad Y,Schultz M H.A generalized m inimal residual algorithm for solving nonsymmetric linear system s[J]. SIAM Journal on Scientific and Statistical Computing,1986,7:856-869.
[7]李劲杰,杨青,杨永年.三维非结构网格Euler方程的LU-SGS算法及其改进[J].计算物理,2006,23(6):748-752.
[8]李春娜,叶正寅.基于二维非结构网格的GMRES隐式算法[J].西北工业大学学报,2007,25(5):630-635.
[9]Jawahar P,Kamath H.A high-resolution procedure for Euler and Navier-Stokes computations on unstructured grids[J]. J Comput Phys,2000,164:165-203.
[10]Orkw is P D,George J H.A comparison of CGS preconditioning methods for New ton’s method solvers[C]//AIAA,1993.
[11]段治健,杨永,马欣荣,等.求解带状线性方程组的一种并行算法[J].计算机科学,2010,37(3):242-244.
[12]曹芳芳,吕全义.解非对称块三对角线性方程组的并行算法[J].西北工业大学学报,2011,29(2):318-322.
[13]K rzysztof J F,Todd A O,James L,et al.P-Multigrid solution of high-order discontinuous Galerkin discretizations of the compressible Navier-Stokes equations[J]. Journal of Computational Physics,2005,207:92-113.
[14]Cristian R N,Dim itri J M.H-order discontinuous Galerkin methods using an hp-multigrid approach[J].Journal of Computational Physics,2006,213:330-357.
[15]Laslo T D,David L D.Preconditioning methods for discontinuous Galerkin solutions of the Navier-Stokes equations[J].Journal of Computational Phsics,2009,228:3917-3935.
DUAN Zhijian1,2
1.Department of Mathematics,Xianyang Normal University,Xianyang,Shaanxi 712000,China
2.National Key Laboratory of Aerodynamic Design and Research,Northwestern Polytechnical University,Xi’an 710072,China
The implicit schemes for solving Euler equation are investigated on unstructured grids,including LU-SGS, GMRES and improved LU-SGS schemes.By Roe numerical flux and Van Albada typed limiter,the traditional LU-SGS and GMRES schemes are explored,and the improved LU-SGS scheme is developed by adding the error compensation of high order term.In addition,the transonic inviscid flow around NACA 0012 airfoil and RAE2822 airfoil as the examples are calculated.The numerical experiments indicate that the error compensation LU-SGS algorithm has the advantages of low storage requirements and easy programming,and the computational efficiency is close to GMRES algorithm and more than 2.5 times of LU-SGS one.
discontinuous Galerkin FEM;LU-SGS algorithm;GMRES algorithm;limiter
A
TP301
10.3778/j.issn.1002-8331.1311-0474
DUAN Zhijian.Efficient implicit algorithm s for discontinuous Galerkin finite elem ent method of Eu ler equation. Computer Engineering and Applications,2014,50(16):21-24.
国家自然科学基金(No.11002117);咸阳师范学院科研基金项目(No.09XSYK 204,No.09XSYK 209)。
段治健(1980—),男,博士,讲师,研究领域为理论与计算流体力学、信息处理中的并行算法。E-mail:zhijian_duan@126.com
2013-12-01
2014-01-28
1002-8331(2014)16-0021-04
CNKI网络优先出版:2014-03-03,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1311-0474.htm l
