基于DCT域内拉普拉斯值排序的人脸识别方法

王永茂，王玉琨，赵珊

河南理工大学计算机科学与技术学院，河南焦作 454000

◎博士论坛◎

基于DCT域内拉普拉斯值排序的人脸识别方法

王永茂，王玉琨，赵珊

河南理工大学计算机科学与技术学院，河南焦作 454000

基于DCT域内的人脸识别方法的关键是如何选择有效的DCT系数，提出了一种基于DCT域内拉普拉斯值排序的人脸识别方法。首先将图像划分为若干个大小相同的子块，对每一个子块进行DCT变换，得到分块DCT系数，然后利用拉普拉斯值作为局部保持能力判据选择那些能够很好保持样本流形结构的分块DCT系数，最后对选定的DCT系数执行LPP算法提取识别特征，在ORL和Yale人脸数据库上的实验结果证明了该方法的有效性。

人脸识别；分块离散余弦变换；局部保持投影；拉普拉斯值

1 引言

在人脸识别等应用领域中经常遭遇“高维数据”，需要进行有效的降维，子空间特征提取方法是一种有效的降维手段。主元成分分析（Principle Component Analysis，PCA）[1]和线性判别分析（Linear Discrim iant Analysis，LDA）[2]是两种典型的线性子空间特征提取方法，但不能很好提取数据的非线性特征，有研究表明，人脸图像很可能位于一个低维的非线性流形上[3]。近年来，基于流形的子空间特征提取方法局部保形投影（Locality Preserving Projection，LPP）[4]被广泛应用到人脸识别中，与PCA及LDA相比，LPP在投影时能够保持样本的局部结构，将人脸图像投影到一个反映其本质的流形结构上，其性能与LDA相当，远优于PCA[5]。然而，由于训练样本个数有限，样本维数往往远大于样本的个数，标准的LPP算法通常陷入小样本问题，因此在应用LPP之前往往利用PCA对样本进行降维，这样实际上仅仅利用主元空间内的信息而丢失了其零空间内的大量信息，为此Feng等人提出了直接局部保形投影算法（Direct LPP，DLPP）[6]。LPP与DLPP本质上是非监督算法，为了充分利用样本的鉴别信息，一些基于LPP的监督算法相继提出，Yu等人结合Fisher准则提出了鉴别保局投影算法[7]，Zhu等人提出正交鉴别保局投影算法[8]，Cai等人在图嵌入框架的基础上提出了局部敏感鉴别分析算法[9]。

离散余弦变换（DCT）是信号处理过程中常见的一种时域频域变换，广泛应用于语音及图像数据压缩领域[10]。DCT的数据压缩能力与PCA相当，并具有快速算法，可以大大降低计算复杂度，基于此，一些基于DCT域内的人脸识别方法应运而生[11-13]。基于DCT域内的人脸识别方法的关键是如何选择有效的DCT系数。现有的方法都是按矩形或“Z”字形顺序选择低频DCT系数作为特征进行人脸识别。本文从有效特征选择的角度出发，提出了一种基于DCT域内拉普拉斯值排序的人脸识别方法，以拉普拉斯值作为局部保持能力判据选择那些能够更好反映样本流形结构的分块DCT系数，然后在选定的分块DCT域内执行LPP算法提取人脸特征。

2 局部保形投影

LPP是特征提取的最有效的方法之一，其基本思想为：在识别问题中，两个样本的欧式距离越小，其相似度越高，那么同属一个类别的可能性就越大，因此LPP的目标是寻找一个转换矩阵V将高维空间RD中的数据集X={x1，x2，…，xN}映射为低维空间Rd(d≪D)中的数据集Y={y1，y2，…，yn}，即yi=VTxi，i=1，2，…，N，使得在RD空间内互为近邻的两点经V映射后在Rd空间中仍互为近邻，LPP的目标公式为：

其中，W=[Wij]为权值矩阵，Wij的取值为：

其中，σ为经验值，Nk(xj)表示样本xj的k近邻集合，W的定义体现了样本的局部信息，即与xi和xj是否为近邻点有关。

最小化式（1）可以通过求解广义特征值问题得到：

其中，D为对角矩阵，其对角元素为W的行（或列）元素之和，即D=；L为Laplacian矩阵，L=D-W。v为V的列向量。假定v1，v2，…，vd为式（3）最小的d个特征值对应的特征向量，则最优的转换矩阵Vopt为：

LPP得到的线性映射为：

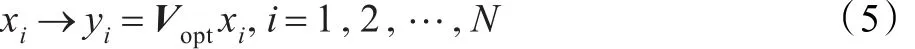
3 分块离散余弦变换

首先讨论一维的情况，对于一个N维向量x，DCT定义为：

DCT可以写成向量形式，即y=CTx，矩阵C∈RN×N的元素cn，k定义为：

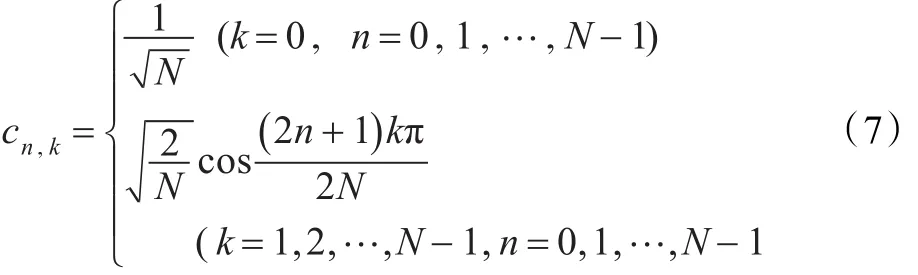
容易证明C为正交矩阵，即有CT=C-1。

下面讨论二维的情况，对于一个M×N的二维矩阵X的DCT结果可以通过在行方向和列方向上进行DCT变换得到，即：

其中CM∈RM×M和CN∈RN×N分别为行方向和列方向上的正交变换矩阵。

二维矩阵X的DCT变换结果为一个与X大小相同的矩阵，称为矩阵X的DCT系数矩阵，图1为一幅人脸图像及其DCT系数矩阵。

图1（b）的DCT系数矩阵很好地体现了其“能量集中”这一特性，即DCT系数矩阵的左上角的数值较大，说明人脸图像主体信息主要集中在DCT系数的低频部分。

图1 人脸图像及DCT系数

在应用LPP算法之前，需要将M×N图像矩阵转换为MN维向量，式（8）可以转换为如式（9）所示的向量形式：

其中ˆ=[x0，0，…，xM-1，N-1]和ˆ=[y0，0，…，yM-1，N-1]为MN维向量，G为MN×MN正交变换矩阵，其值为：

此外，向量ˆ中元素的序列对应于变换矩阵G的列顺序，因此中元素序列的改变不会改变变换矩阵G的正交性。

对于JPEG压缩标准，首先将图像划分为若干个大小为8×8的子块，然后再对各个子块分别执行DCT变换。同样，对于一个大小pn×qn的图像若划分为p×q个大小为n×n的子块，则其分块DCT变换可以表示为：

其中Gij为对每一个子块进行DCT变换时对应的变换矩阵，可知Gij为正交矩阵，即有=，所以有：

可知式（12）对应的块对角变换矩阵同样也为正交矩阵，所以分块DCT系数可以直接应用LPP算法。

对图像进行分块DCT变换得到的分块DCT系数同样也是二维的，在应用LPP时，样本的特征采用一维向量的形式表示，因此需要将分块DCT系数按照一定的次序转换为一维向量形式，通常有两种方式：如图2所示的矩形方式（矩形内的DCT系数按行或列顺序排列，本图中为按行排列）和如图3的“Z”字形方式。

图2 DCT系数选择方法（矩形）

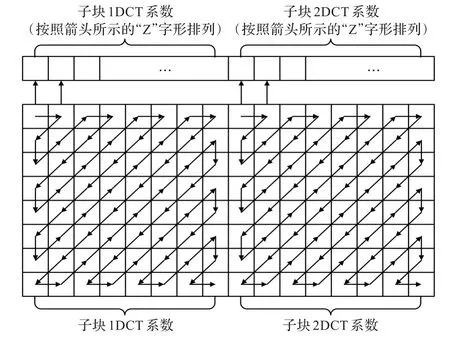
图3 DCT系数选择方法（“Z”字形）

4 基于拉普拉斯值的特征选择算法

从有效特征选择的角度出发提出采用拉普拉斯值（Laplacian Score，LS）作为局部保持能力判据选择能更好刻画样本流形结构的DCT系数。

LS用于评价特征的局部保持能力，本质上与LPP相似[14-15]。令fri为第i个样本xi的第r个特征，i=1，2，…，N，LS计算过程如下：

（1）构造近邻图G：如果样本xi与样本xj互为近邻点，那么xi与xj之间有一条边相连。

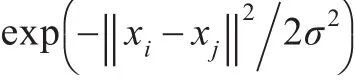
（3）对于第r个特征fr=[fr1，fr2，…，frN]T，其LS值定义为：

其中，Var(fr)为第r个特征的方差，经过简单变形，式（13）变为：

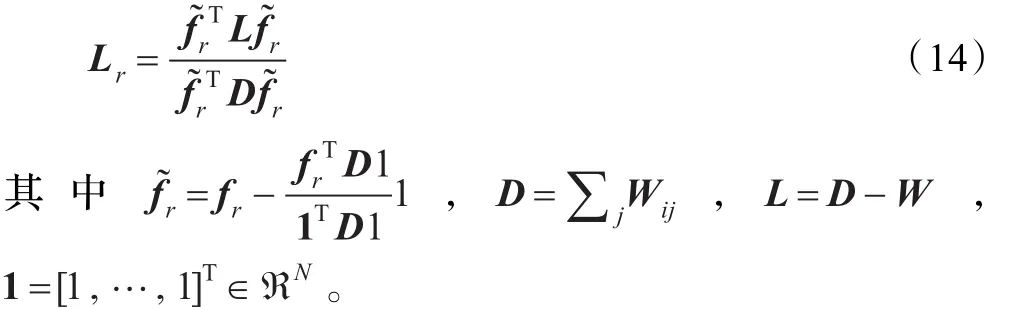
根据式（13）中LS的定义，一个好的特征，应该使得∑ij(fri-frj)Wij最小化，Var(fr)最大化，LS值趋向取较小的值。∑ij(fri-frj)Wij最小化表明该特征具有较强局部信息保持能力，即互为近邻点的两个样本点在该特征上差别最小；Var(fr)最大化表明该特征具有较强样本表示能力。因此可以将LS作为局部保持能力判据，其值越小，表明该特征刻画样本流形结构的能力越强。同样在执行LPP算法之前，将分块DCT变换得到的分块DCT系数按照LS值从小到大的顺序转换为一维向量形式，如图4所示。

图4 基于LS的DCT系数选择

5 提出的方法

本文提出基于DCT域内拉普拉斯值排序的人脸识别方法（DCT/LS+LPP）的流程如图5所示，包括两个阶段：训练阶段和识别阶段。

图5 DCT/LS+LPP的图像识别框图

在训练阶段，首先对训练集中每一幅图像划分若干个大小为n×n的子块，然后对各个子块进行DCT变换，得到分块DCT系数，对于每一个分块DCT系数，在不同频率的DCT系数上计算其LS值作为局部保持能力判据，按LS值从小到大进行排序，最后将每一个分块DCT系数中LS值较小的DCT系数组合成一个一维向量作为图像的特征执行LPP算法，得到最优投影矩阵和训练样本的识别特征。

在识别阶段，对于一幅测试的图像，同样首先将其划分为若干个大小为n×n的子块，然后对每一个子块进行DCT变换，求出其分块DCT系数，然后在每一个子块内依据训练阶段中的次序选择DCT系数，并将每一个子块所选取的DCT系数组成的一维向量在训练阶段获得的最优投影矩阵的投影结果作为图像的识别特征，最后利用欧式距离作为相似度度量的最近邻分类器完成对测试图像的分类。

6 实验与分析

为了验证算法的有效性，本章在ORL和Yale人脸库上进行实验：（1）比较不同的DCT系数选择方法的识别性能；（2）比较PCA+LPP，DLPP和DCT+LPP识别性能。

6.1 ORL人脸数据库的实验

ORL人脸库是由英国剑桥大学建立，共有40个人，每人10张图像，共有400张人脸图像，图像的面部表情和面部细节有着不同程度的变化，人脸姿势也有相当的程度变化，比较充分反映了同一人不同人脸图像的变化和差异。图6是ORL人脸库的部分样本，实验使用的人脸图像经剪切后大小均为32×32，然后将两个人脸库中的每个图像进行标准化。

图6 ORL人脸数据库中的部分人脸图像

实验1首先比较不同的DCT选择方法的识别性能。随机选取每一个人的5幅图像组成训练样本集，剩余的图像组成测试样本集，首先将训练样本集中每一幅图像划分为8×8子块，这样每一幅图像可以得到16幅子块，然后对每一幅子块进行DCT变换，每一幅子块对应64个DCT系数。分别使用三种方法对DCT系数进行选择：一种是如图2所示的选取子图像的DCT系数中低频部分的一个矩形子块，一种是如图3所示的按照“Z”字形顺序选取DCT系数，另一种就是本文提出的根据LS值从小到大顺序进行选择，在计算LS值时，近邻点个数k=4（训练样本集中每一个人的人脸图像个数-1），图7为每一幅子图像从上到下从左到右对应的分块DCT系数的LS值。

从图7可以看出，从低频DCT系数到高频DCT系数，其对应的LS值的变化并不是单调递增的，而呈现出一种“震荡式”变化趋势，也就是说低频的DCT系数的局部保持能力不一定低于高频的DCT系数，因此采用“矩形”或“Z”字形对DCT系数进行选择，并不能将具有较强局部保持能力的DCT系数选择出来。这里根据DCT系数的LS值按照从小到大的顺序进行选择。

在选定DCT系数后，利用基于欧式距离进行相似度度量的最近邻分类器进行分类，上述过程重复10次，将平均识别率作为最终的识别结果，表1为在不同的DCT选择方法下平均识别率随DCT系数个数的变化情况（表中标出为每一个子图像选取的DCT系数对应的个数）。

表1 不同的DCT选择方法的识别率比较（%）

从表1可以看出，对于基于矩形的DCT选择方法，在每一个子图像内选取9个DCT系数时，达到了该方法最高识别率88.7%；对于基于“Z”字形的DCT选择方法，同样也是在每一个子块内选取9个DCT系数时，达到了该方法的最高识别率88.65%；采用本文提出的基于LS值的DCT系数选择方法，在每个子图像内选取4个DCT系数时，就达到了最高识别率89.6%。所以从最高识别率看，本文提出的基于LS的DCT系数选择方法在使用最少的DCT系数的情况下得到了最高的识别率。从整体来看，基于矩形与“Z”字形的DCT选择方法的识别效果相当，而效果最好的是本文提出的基于LS的DCT系数选择方法，其性能在大部分情况下均优于另外两种特征选择方法。

实验2比较PCA+LPP，DLPP，DCT/Z+LPP（利用Z字形进行DCT系数选择），DCT/LS+LPP。实验中，每人分别随机选取5幅图像组成训练样本集，其余图像组成测试样本集，采用最近邻分类器进行分类，重复进行10次，取平均值作为最终的识别结果。在PCA+LPP方法中，PCA阶段保持99%的主元能量，在DCT/Z+LPP和DCT/LS+LPP方法中，DCT系数的个数为实验1中最高识别率对应的DCT系数个数，分别为9和4。表2为LPP在PCA和DCT正交变换域内的平均识别率及其对应的维数。

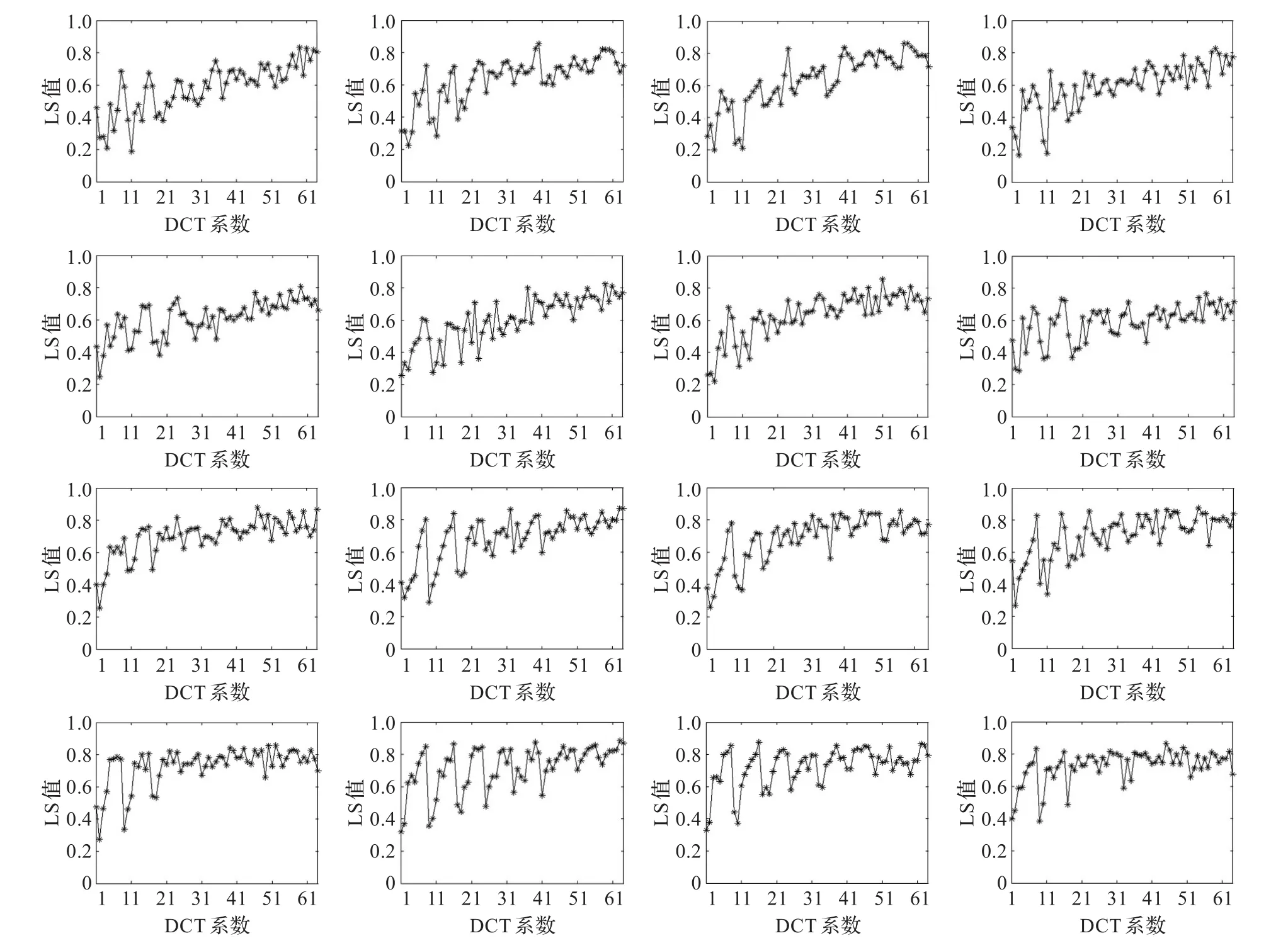
图7 子图像的DCT系数对应的LS值

表2 LPP在PCA和DCT正交变换域内的平均最高识别率

从表2可以看出：（1）在DCT变换域内执行LPP算法的最高识别率高于在PCA变换域内执行LPP算法以及DLPP算法。（2）不管是按照“Z”字形顺序选择DCT系数还是基于LS值进行DCT系数选择，对选定的DCT系数执行LPP算法其识别率均高于直接在DCT变换域内进行识别（结果如表1所示）。

6.2 Yale人脸数据库的实验

Yale人脸库由美国耶鲁大学建立，包含15个人，每人11张图像，共有165张人脸图像，主要包括光照条件的变化，表情的变化及有无眼睛修饰等。图8是Yale人脸库的部分样本，实验使用的人脸图像经剪切后大小均为32×32，然后将两个人脸库中的每个图像进行标准化。

图8 Yale数据库中的部分人脸图像

在实验中，从每类人脸图像中随机选取l（l=3，4，5）张图像组成训练样本集，剩余的图像组成测试样本集，重复进行10次，得到10组不同的训练样本集和测试样本集。分别采用PCA+LPP，DCT/Z+LPP和DCT/LS+ LPP等算法进行特征提取，对于PCA+LPP算法，在PCA阶段保持99%的主元能量，对于DCT/Z+LPP和DCT/ LS+LPP，在计算LS值以及执行LPP算法时，近邻点个数k=l-1，最后利用欧式距离进行相似度度量的最近邻分类器对测试图像进行分类。表3为Yale人脸库的10组不同的人脸图像划分上得到的平均最高识别率以及对应的DCT系数个数和目标维数。

从表3可以看出：从平均最高识别率看，在不同的训练集下，DCT/Z+LPP和DCT/LS+LPP的性能始终优于PCA+LPP与DLPP，另一方面，由于本文提出的算法利用基于LS值的局部保持能力判据选择有效的DCT系数，因此DCT/LS+LPP在使用较少的DCT系数的情况下得到了比DCT/Z+LPP更高的识别率。

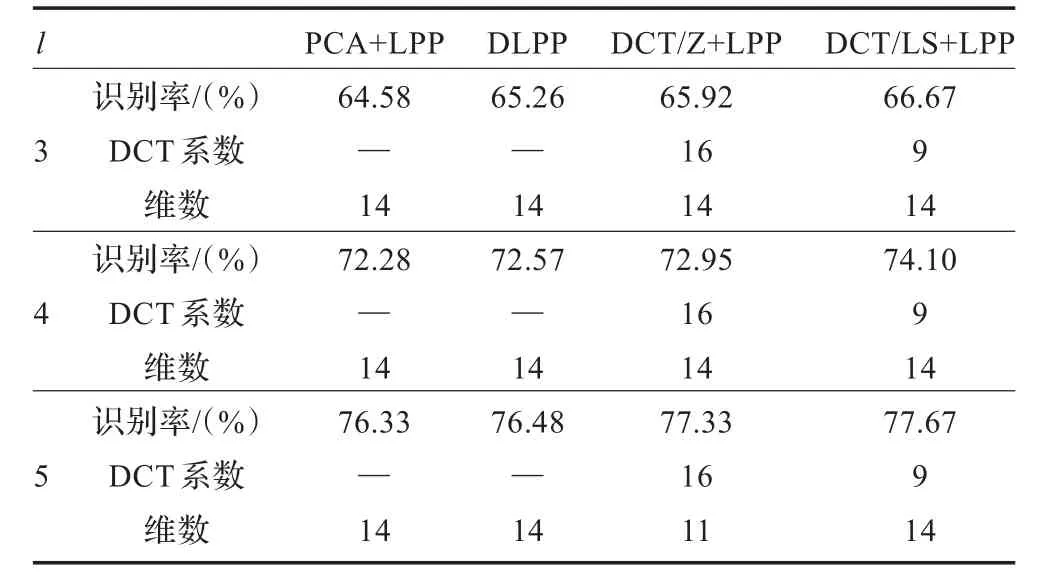
表3 Yale人脸库上的识别性能对比

7 结束语

本文提出了一种DCT域内拉普拉斯值排序的人脸识别方法，利用拉普拉斯值特征选择算法作为局部保持能力判据在DCT域内对分块DCT系数进行选择，进而在选定的DCT系数上执行局部保持投影，实验验证了提出方法的有效性。

[1]Turk M，Pentland A.Eigenfaces for recognition[J].Journal of Cognitive Neuroscience，1991，3（1）：72-86.

[2]Martinez A M，Kak A C.PCA versus LDA[J].IEEE Trans on Pattern Analysis and Machine Intelligence，2001，23（2）：228-233.

[3]Belkin M，Niyogi P.Laplacian eigenmaps for dimensionality reduction and data representation[J].Neural Computation，2003，15（6）：1373-1396.

[4]He XF，Yan SC，Hu YX，et al.Face recognition using Laplacianfaces[J].IEEE Trans on Pattern Analysis and Machine Intelligence，2005，27（3）：328-340.

[5]Bajwa U I，Taj I A，Bhatti Z E.A comprehensive comparative performance analysis of Lap lacianfaces and Eigenfaces for face recognition[J].Imaging Science Journal，2011，59（1）：32-40.

[6]Feng G Y，Hu D W，Zhou Z T.A direct locality preserving projections（DLPP）algorithm for image recognition[J]. Neural Processing Letters，2008，27（3）：247-255.

[7]Yu W W，Teng X L，Liu C Q.Face recognition using discriminant locality preserving projections[J].Image and Vision Computing，2006，24（3）：239-248.

[8]Zhu L，Zhu S A.Face recognition based on orthogonal discriminant locality preserving projections[J].Neurocomputing，2007，70（7）：1543-1546.

[9]Cai D，He X F，Zhou K，et al.Locality sensitive discriminant analysis[C]//International Joint Conference on Artificial Intelligence，Hyderabad，India，2007：708-713.

[10]Ziad M，Martin D.Face recognition using the discrete cosine transforms[J].International Journal of Computer Vision，2001，43（3）：167-188.

[11]Zheng Z L，Zhao J M.Locality preserving projection in orthogonal domain[C]//Congress on Images and Signal processing，Sanya，Hainan，China，2008：613-617.

[12]胡永刚，吴翊，王洪志，等.高维数据降维的DCT变换[J].计算机工程与应用，2006，42（32）：21-30.

[13]Chen Weilong，Er Meng Joo，Wu Shiqian.PCA and LDA in DCT[J].Pattern Recognition Letters，2005，26（15）：2474-2482.

[14]He XF，Cai D，Niyogi P.Lap lacian score for feature selection[C]//Advances in Neural Information Processing System，Vancouver，British Columbia，Canada，2005：507-514.

[15]Huang H，Feng HL，Peng CY.Com plete local fisher discriminant analysis with laplacian score ranking for face recognition[J].Neurocomputing，2012，89（7）：64-77.

WANG Yongmao,WANG Yukun,ZHAO Shan

School of Computer Science and Technology,Henan Polytechnic University,Jiaozuo,Henan 454000,China

The key of face recognition in DCT domain is how to select effective DCT coefficient.For this purpose，a method for face recognition in DCT domain with Laplacian Score ranking is proposed.Firstly，the image is divided into several blocks with the same size.For each block，DCT is used to obtain block DCT coefficient.Then effective block DCT coefficient is selected according to locality preserving power criterion with Laplacian Score.Ultimately，LPP is performed on the selected block DCT coefficients to extract recognition features.The experiments on ORL and Yale face database shows that the improved method is effective.

face recognition;block DCT;locality preserving projection;Laplacian score

A

TP391.4

10.3778/j.issn.1002-8331.1312-0271

WANG Yongmao,WANG Yukun,ZHAO Shan.Face recognition in DCT domain with Lap acian score ranking. Computer Engineering and Applications,2014,50（16）：1-6.

河南省教育厅科学技术研究重点项目（No.12B520021）。

王永茂（1976—），男，博士，副教授，研究领域为图像处理及模式识别；王玉琨（1960—），男，教授，研究方向为计算机图形学；赵珊（1975—），女，博士，副教授，研究方向为图像处理与模式识别。E-mail：w ym yjs2000@hpu.edu.cn

2013-12-19

2014-02-18

1002-8331（2014）16-0001-06

CNKI网络优先出版：2014-02-26,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1312-0271.htm l