伺服系统在连续式飞剪系统中的设计与应用

陈冬玲

（柳州职业技术学院机电工程系，广西柳州545006）

伺服系统在连续式飞剪系统中的设计与应用

陈冬玲

（柳州职业技术学院机电工程系，广西柳州545006）

伺服系统采用先进的数学模型，精确计算飞剪剪切的各项控制参数，实现飞剪的自动剪切、碎断、定位和采样功能。该数学模型包括飞剪剪切长度计算模型与转辙器定位计算模型。应用结果表明，该数学模型能够在运行中获得良好的动态性能，将轧件的平均剪切误差控制在5 cm以内，提高了产品的成材率与产量。

连续式；伺服系统；飞剪；数学模型

精轧飞剪是高线生产工艺线上的关键设备，其工作稳定性及剪切精度和响应速度都将直接影响整条高线的生产，并对产品质量与成材率有很大的影响。近几年来，高速线材生产线上的飞剪都是采用普通的起停式飞剪，该类型飞剪都存在剪切速度不高，剪切精度低下，系统响应慢，传动装置与电机承受较大冲击电流、飞剪定位慢等缺点。针对这些问题，本文采用了一种新型的连续式回转飞剪。该飞剪是以伺服控制器为控制核心，通过剪切长度计算模型与转辙器定位计算模型来进行速度环和位置环的调节，从而进一步提高了系统的控制精度和响应速度。

1 飞剪控制系统原理及剪切过程

飞剪控制系统主要由主剪机、转辙器、热金属检测器HMD、定位编码器、全数字交流调速装置6SE70和S120变频器、PLC、伺服控制器、人机画面HMI等单元组成。图1所示为高线连续式飞剪系统的结构图。

图1 飞剪系统结构图Fig.1 The architecture diagram of flying shear

1.1 飞剪启动过程

飞剪是否满足启动条件，何时达到启动要求以及主剪的速度给定值都是由S7-300 PLC系统判断和计算产生的。主剪启动后，以HMI中设定的超前率乘以出口机架的实际值作为主剪的速度给定值连续旋转，同时定位编码器1将主剪剪刃的位置信息实时反馈到伺服控制器中，转辙器回到等待位并通过定位编码器2将转辙器的位置信息实时反馈到伺服控制器中。

1.2 飞剪切头过程

飞剪自动切头时，在轧件到达HMD1之前，主剪以设定超前速度旋转，转辙器在“等待位”待机。当轧件头部到达HMD1位置时，伺服控制器快速读取主剪剪刃的定位编码器1的位置值，利用数学模型计算出剪刃的所需位置和预计位置，并算出两个位置之间的偏差值，再通过PROFIBUS将该偏差值传至PLC，PLC再根据偏差值对主剪速度值进行调整，使轧件在到达HMD2时的剪刃实际位置值与期望位置值相互一致。当轧件头部到达HMD2位置时，伺服控制器快速读取转辙器的定位编码器2的位置值，利用数学模型计算出转辙器的启动延时时间。延时完成后，伺服控制器向S120传动输出一个模拟量型的速度给定值，转辙器则快速地从等待位经过剪切位到达通过位，在剪切位被剪切的轧件头部被抛向碎断剪进行碎断，在通过位的剩余轧件将进入精轧机。

1.3 飞剪切尾过程

飞剪自动切尾时，主剪以设定滞后速度旋转，转辙器在“通过位”待机。当轧件尾部到达HMD1位置产生下降沿信号时，主剪以类似于切头过程的方式进行速度调整。当轧件尾部到达HMD2位置产生下降沿信号时，转辙器也以类似于切头过程的方式将从等待位快速地经过剪切位到达等待位，在剪切位被剪切的轧件尾部被抛向碎断剪进行碎断，至此飞剪进入到下一个工作周期。

1.4 飞剪碎断过程

飞剪在进入碎断状态时，转辙器将移动至“碎断位”，把轧件送至碎断剪。主剪的碎断速度包含了一个切头速度的超前速度，以防止轧制过程中轧件回头造成堆钢。在碎断状态解除后，转辙器将沿顺时针方向移动至“等待位”待机。

2 飞剪过程控制数学模型

2.1 切头长度计算模型

若轧件头部的速度为vh，头部剪切的超前率为h，则飞剪的切头速度vC为

当轧件头部到达HMD1时，伺服控制器接收到HMD1的一个上升沿信号后，开始预测轧件头部到达HMD2时主剪剪刃的位置，再根据切头长度与HMD2和主剪之间的距离计算出轧件头部到达HMD2时主剪剪刃的期望位置，从而最后计算出主剪剪刃需要调整的位置变化量，并转换为速度调节量。公式如下：

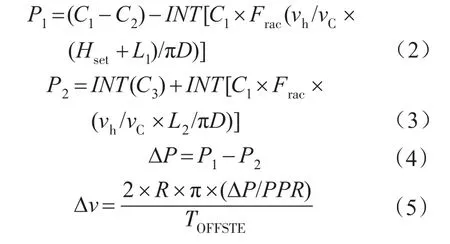
式中：P1为轧件头部到达HMD2时剪刃的期望位置值；P2为预测轧件头部到达HMD2时剪刃的预测位置；ΔP为剪刃需要调整的位置变化量；C1为主剪剪刃转一周时的定位编码器1的位置值；C2为主剪剪切角的位置值；C3为轧件头部到达HMD1时剪刃的实际位置值；Hset为切头长度设定值；L1为HMD2和主剪之间的距离；D为主剪剪刃直径；L2为HMD1与HMD2之间的距离；INT()为取整函数，Frac()为取余函数；Δv为需要调整的速度；R为主剪剪刃半径；PPR为主剪剪刃转一圈的总脉冲数；tOFFSTE为主剪剪刃速度的调节时间。

2.2 切尾长度计算模型

若轧件尾部的速度为vt，尾部剪切的滞后率为q，则飞剪的切尾速度为

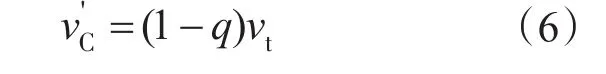
当轧件尾部到达HMD1时，伺服控制器接收到HMD1的一个下降沿信号后，开始预测轧件头部到达HMD2时主剪剪刃的位置，再根据切头长度与HMD2和主剪之间的距离计算出轧件尾部到达HMD2时主剪剪刃的期望位置，从而最后计算出主剪剪刃需要调整的位置变化量。公式如下：

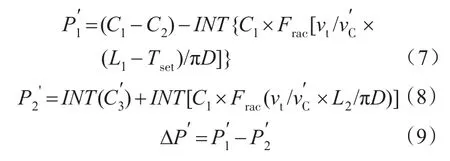
2.3 转辙器定位计算模型

当轧件头部到达HMD2时，伺服控制器接收到HMD2的一个上升沿信号后开始启动计时器，当计时器达到切头延时计算值后，转辙器快速地从等待位经过剪切位到达通过位；当轧件尾部到达HMD2时，伺服控制器接收到HMD2的一个下降沿信号后又开始启动计时器，当计时器达到切尾延时计算值后，转辙器快速地从通过位经过剪切位到达等待位。公式如下：

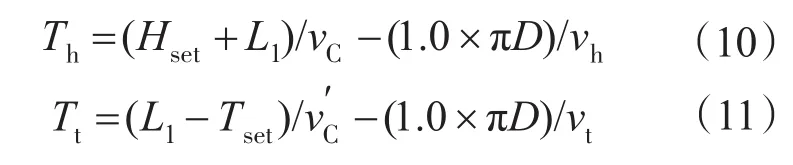
式中：Th为切头延时计算值；Tt为切尾延时计算值。

2.4 转辙器速度计算模型

当轧件头部经过HMD2时，伺服控制器立刻采样主剪的速度作为主轴速度，转辙器伺服电机作为辅轴，并以1∶1的比例跟随主轴速度迅速移动至通过位；当轧件尾部到达HMD2时，伺服控制器仍然以主剪的速度作为主轴速度，转辙器伺服电机作为辅轴，并以1∶1的比例跟随主轴速度迅速移动至碎断位，再以低速从碎断位移至等待位，如图2所示。

图2 飞剪速度追踪曲线Fig.2 Speed trace curve of flying shear

具体公式如下：

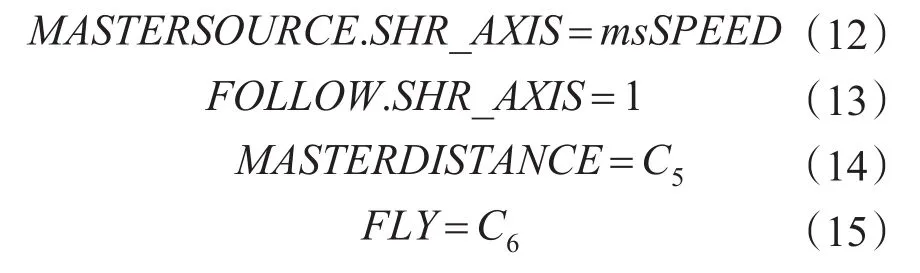
式中：MASTERSOURCE.SHR_AXIS为以主剪为主轴；FOLLOW.SHR_AXIS为主轴与辅轴的比例值；MASTERDISTANCE和FLY为在主轴移动C5的位移量的时间段内，辅轴必须移动C6的位移量。

3 连续式飞剪工程控制应用

本文以柳钢二高连轧生产线上的3#飞剪为研究对象，其数学模型参数为：主剪剪刃直径D= 800 mm，HMD1与HMD2之间的距离L2=17 900 mm，HMD2和主剪之间的距离L1=6 200 mm，切头速度vC和切尾速度控制在25m/s以下，主剪剪刃速度的调节时间TOFFSTE=1 s。该控制系统经过调试后，不仅可靠性高，剪切速度也可以达到20m/s，轧件的平均剪切误差控制在5 cm以内，具有良好的动态特性。剪切过程图如图3、图4所示。

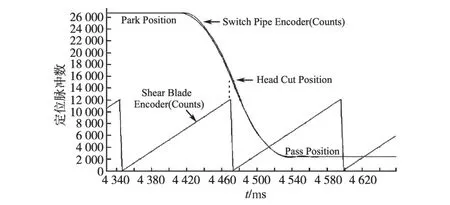
图3 飞剪切头过程图Fig.3 Head cutting diagram of flying shear

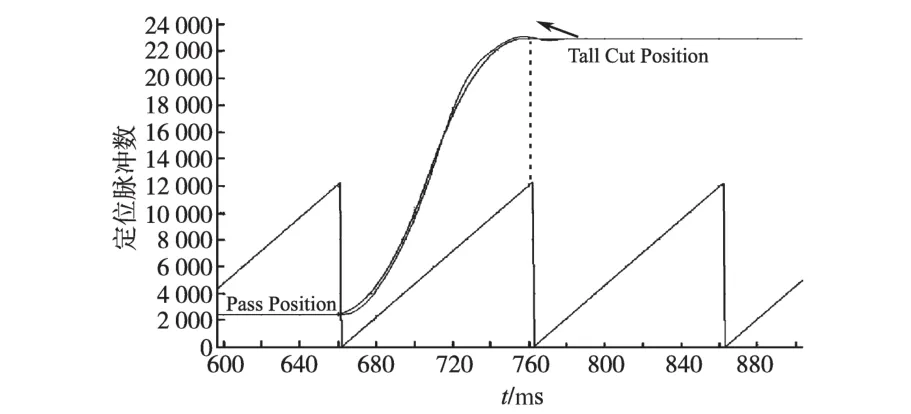
图4 飞剪切尾过程图Fig.4 Tail cutting diagram of flying shear

4 结论

高精度的飞剪控制系统是轧钢电气控制系统中最复杂、最有价值的部分，在提高产品的成材率与产量方面起着重要的作用。本文所设计的飞剪控制系统比传统的起停式飞剪有着更高的剪切精度，更快的系统响应速度和剪切速度柳钢二高线自2010年投产以来，系统运行稳定增强了企业的竞争力。

［1］蔡志军，陈劲松，张磊.高速线材飞剪的自动化控制［J］.安徽机电学院学报，2001，16（4）：61-65.

［2］郎兵，任雪梅.棒材生产线起/停式倍尺飞剪的工作原理［J］.莱钢科技，2003，9（3）：31-33.

［3］张梅，王万新，王庭宽，等.T400剪切工艺板实现飞剪控制［J］.电气传动，2006，36（6）：58-60.

Design and Application of Servo System in the Continuous Flying Shears System

CHEN Dong-ling
（Department of Mechatronics Engineering，Liuzhou Vocational&Technical College，Liuzhou 545006，Guangxi，China）

In servo system，advanced mathematic model was adopted to accurately calculate each control parameter of flying shear，so that automatic cutting，cobbling，positioning and sampling functions of flying shears were achieved.Mathematical model included shearing cutting length calculation and switch pipe positioning calculation. Application results show that the control model can acquire to moving state performance goodly in the movement，and average cutting tolerance of rolled strip is controlled within 5 cm，so that product output and economic benefits is improved.

continuous；servo system；shear；mathematic model

TG334.9

B

2013-12-25

修改稿日期：2014-06-21

广西质量控制工程项目（LGQC-BX-1250）

陈冬玲（1971-），女，硕士研究生，高级工程师，Email：huangbin88888888@163.com