机载单站对运动目标无源定位跟踪算法
2014-07-07李炳荣马强王欣欣
李炳荣,马强,王欣欣
(1.海军航空工程学院a.电子信息工程系;b.训练部,山东烟台264001;2.烟台大学光电学院,山东烟台264005)
机载单站对运动目标无源定位跟踪算法
李炳荣1a,马强1b,王欣欣2
(1.海军航空工程学院a.电子信息工程系;b.训练部,山东烟台264001;2.烟台大学光电学院,山东烟台264005)
针对无源定位系统中,机载单站相对于运动辐射源目标作为状态模型,在测方位角及其变化率基础上,引入多普勒频率变化率参数构建观测模型。常用的扩展卡尔曼滤波(EKF)存在不稳定和精度低的问题,采用修正增益的扩展卡尔曼滤波算法(MGEKF),找出修正函数矩阵,实现定位状态滤波估计。仿真结果表明,MGEKF算法较之EKF算法有较高的定位精度和较快的收敛速度。
单观测站;机载;运动辐射源;无源定位;修正增益卡尔曼滤波算法
无源定位系统一般为非线性系统,因而常用于解决高斯噪声模型下线性系统递推估计的卡尔曼滤波方法无法直接应用。为此,将非线性系统加以线性化,从而采用扩展卡尔曼滤波(EKF),可以得到无源定位问题的解决办法[1-6]。但EKF的应用效果严重地依赖于初始状态估计的精度,并且定位误差较大,常常出现定位估计发散的情况。为了克服EKF的不足,在实用中需要进行相应的改进[7-10]。修正增益的扩展卡尔曼滤波(MGEKF)算法是较为有效的一种改进方法,它利用当前的观测值来修正滤波增益,并改良滤波协方差,从而使估计精度得到提高。将方位测量和多普勒频率测量相结合,运用MGEKF算法进行递推估计,对于机载单站对运动辐射源无源定位与跟踪的问题是一种较好的解决方法。
1 系统的状态模型与观测模型
在三维空间中,利用一个运动平台上安装的接收机,测量信号的到达方位角及其变化率,同时,测量目标到达信号的多普勒频率及其变化率,对目标T的位置进行估计,跟踪其运动轨迹。对于飞行目标处于巡航时的情况,假设其处于匀速直线运动状态,并以扰动加速度反映状态瞬变[11]。
采用相对坐标系,以观测器为原点,记为O,xy平面平行于地平面,z轴垂直于地平面,目标T在三维空间中运动,如图1所示。观测器的状态以矢量XO表示,目标的状态以矢量XT表示,则目标相对于观测器的状态矢量为X=XT-XO。相对坐标系对于构建观测模型较为方便,但状态模型较为复杂,总的来看,应用相对坐标系对于研究运动观测站对运动辐射源的无源定位问题较为有利。

图1 无源定位系统的相对坐标系Fig.1 Relative coordinate of passive location system
图1中,vT为目标速度矢量,vO为观测站速度矢量,rk为k时刻观测站与辐射源的距离矢量,β为相对坐标系下的方位角,ε为相对坐标系下的俯仰角。
1.1 状态模型

于是,无源定位系统的状态方程写成:

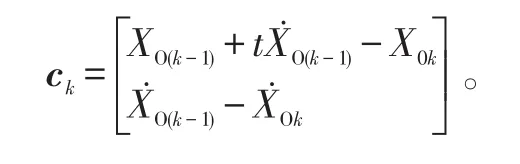
Wk是系统的扰动噪声,其协方差阵为

式(2)的状态方程说明,目标的相对状态与观测器的运动有关,它是通过ck起作用的,因而称ck为控制项。为此,实际状态模型应表示为
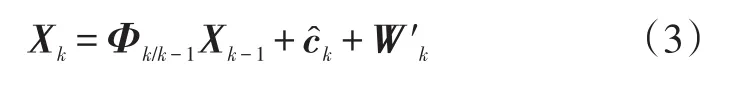
式(3)中,系统误差W′k为式(2)中的误差Wk与控制项ck的估计误差c˜k=ck-c^k之和。
1.2 观测模型
该系统中,观测量包括方位角β、方位角变化率β˙、俯仰角ε、俯仰角变化率ε˙以及多普勒频率变化率f˙d。
根据观测站与目标间的几何关系,有:

当观测站与目标有相对径向速度时,接收到的信号频率是辐射源发射信号频率与多普勒频率之和。假设辐射源发射信号的载波频率固定不变,依据质点运动学原理,可得到多普勒频率变化率的近似表达式为[13]
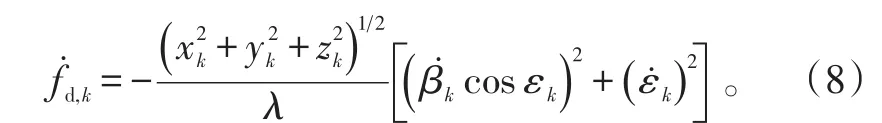
于是,系统的观测方程可以写成:

显然,观测方程式(9)非线性。
2 EKF和MGEKF算法
首先,对式(9)中h(Xk)进行线性化,将其在X^k/k-1展成泰勒级数:


于是,式(9)的观测方程可以表示成下面的线性化形式:

由式(3)和式(12)组成的状态方程和观测方程中,W′k和Vk假定为互不相关的零均值高斯噪声。利用EKF算法进行递推,即可解得目标的状态量,实现无源定位。所使用的递推公式为[14]:

式(13)中,Rk=E[VkVTk]为观测误差的协方差矩阵。
由于EKF算法受观测噪声影响大,且对初值误差敏感,协方差容易出现病态,导致滤波发散,在模型误差较大的情况下,常表现出不稳定性。MGEKF是对EKF的一种改进方法,应用的前提是要解决观测方程中修正函数的问题。
如果存在g(Zk,X^k),使得下式成立:

则称h(Xk)为可修正的,或当Xk→X^k时,上式成立,称h(Xk)为近似可修正的,g(Zk,X^k)就是修正函数矩阵。
为了求得修正函数矩阵g(Zk,X^k),将式(9)中h(Xk)在当前状态估计值X^k处对Xk求偏微分,得:


利用新的滤波增益Kk和状态估计协方差矩阵Pk,求得新的滤波估计值,其精度得到进一步提高。这就是MGEKF算法的优势所在。
从以上过程可以看出,MGEKF算法的计算量大大增加了,它是在EKF计算的基础上,利用其得到的估计值,求得修正增益,然后计算新的Kk和Pk,再用来重新求取状态估计值。所以,MGEKF算法对状态估计性能的提高,实际上是以增大计算量为代价的。
3 计算机仿真
仿真条件:辐射源目标与观测站之间的相对运动速度为(50 m/s,50 m/s,0 m/s),瞬时扰动噪声δx˙=δy˙=δz˙=1 m/s2,δβ=δε=2°,δβ˙=δε˙=0.01(°)/s, δfd=0.3Hz,δf˙d=0.5Hz/s,λ=3cm(f=10 GHz),观测间隔时间t=1 s。分别利用EKF算法和MGEKF算法,在观测站与目标的相对距离为100km时,对相对距离误差和相对速度误差进行估计,并与CRLB进行比较,做100次Monte-Carlo仿真,得到的仿真曲线如图2及图3所示。

图2 相对距离估计误差仿真曲线Fig.2 Simulation curve of estimate error in relative range

图3 相对速度估计误差仿真曲线Fig.3 Simulation curve of estimate error in relative velocity
4 结论
仿真结果表明,利用方位角及其变化率和多普勒频率变化率信息,可以在较短的时间内,估计出运动辐射源目标的位置和速度,利用MGEKF算法,较EKF算法收敛更快,定位跟踪精度更高。因此,在传统的测方位和测频率基础上,利用方位角变化率信息,结合多普勒频率及其变化率的测量,运用MGEKF进行递推和滤波,是解决单个机载观测站对运动辐射源无源定位与跟踪的一种较为理想的方法。
[1]郭福成,孙仲康,安玮.利用方向角及其变化率对固定辐射源的三维单站无源定位[J].电子学报,2002,30(12):1885-1887.GUO FUCHENG,SUN ZHONGKANG,AN WEI.Single observer passive location of 3-D fixed emitter using direction and its rate of changing information[J].Acta Electronics Sinica,2002,30(12):1885-1887.(in Chinese)
[2]SHALOM Y B,LI X R,THIAGALINGAM K.Estimation with applications to tracking and navigation[M]. New York:Wiley,2001:381-394.
[3]单月晖,孙仲康,皇甫堪.单站无源定位跟踪现有方法综述[J].航天电子对抗,2001,17(6):4-7. SHAN YUEHUI,SUN ZHONGKANG,HUANGPU KAN.Passive location and tracking of existing Methods [J].Aerospace Electronic Warfare,2001,17(6):4-7.(in Chinese)
[4]韩令军,田增山,孙冬梅.基于EKF算法的单站无源定位跟踪研究[J].空间电子技术,2009,6(3):39-42. HAN LINGJUN,TIAN ZENGSHAN,SUN DONGMEI. Research for passive location and tracking algorithm of one station based on EKF algorithm[J].Space Electronic Technology,2009,6(3):39-42.(in Chinese)
[5]李莉.伪线性卡尔曼滤波在目标被动跟踪中的应用[J].软件导刊,2009,8(11):30-32. LI LI.The application of pseudo-linear kalman filter in target's passive tracking[J].Software Guide,2009,8(11):30-32.(in Chinese)
[6]王炎滨,袁仁清,杨云志.一种基于扩展卡尔曼滤波的方位跟踪算法[J].电讯技术,2006,46(2):148-151. WANG YANBIN,YUAN RENQING,YANG YUNZHI. An azimuth tracking approach based on extended Kalman filteralgorithm[J].TelecommunicationEngineering,2006,46(2):148-151.(in Chinese)
[7]郭福成,孙仲康,安玮.对运动辐射源的单站无源伪线性定位跟踪算法[J].宇航学报,2002,23(5):28-31. GUO FUCHENG,SUN ZHONGKANG,AN WEI.Passive pseudo-linear location and tracking algorithm of one station for moving radiant point[J].Journal of Astronautics,2002,23(5):28-31.(in Chinese)
[8]王鼎,隋红波,吴瑛.两站基于角度和时差信息的伪线性卡尔曼滤波算法及其改进[J].信号处理,2008,24(2):254-258. WANG DING,SUIHONGBO,WU YING.The pseudolinear Kalman filter algorithm and its improvement based on DOA and TDOA measurements for two stations[J]. Signal Processing,2008,24(2):254-258.(in Chinese)
[9]JULIER S J,UHLMANN J K.A new approach for filtering nonlinear system[C]//Proceedings of the 1995 American Control Conference.Seattle WA,1995:1628-1632.
[10]SONG T L,SPEYER J L.A stochastic analysis of a modified gain extended Kalman filter with applications to estimation with bearings only measurements[J].IEEE Transactions onAutomatic Control,1985,30(10):940-949.
[11]李宗华,肖予钦,周一宇.利用频域和空域信息的单站无源定位跟踪算法[J].系统工程与电子技术,2004,26(5):613-616. LI ZONGHUA,XIAOYUQIN,ZHOU YIYU.Single observation passive location and tracking algorithms using frequency and spatial measurements[J].Systems Engineering and Electronics,2004,26(5):613-616.(in Chinese)
[12]刘延峰,潘泉.干涉仪对辐射源快速精确定位方法研究[J].系统仿真学报,2005,17(6):1525-1527. LIU YANFENG,PAN QUAN.An fast and accurate positioning method for radiation source interferometer[J]. Journal of System Simulation,2005,17(6):1525-1527.(in Chinese)
[13]刁鸣,王越.基于多普勒频率变化率的无源定位算法研究[J].系统工程与电子技术,2006,28(5):696-698. DIAO MING,WANG YUE.Research of passive location based on the doppler changing rate[J].Systems Engineering and Electronics,2006,28(5):696-698.(in Chinese)
[14]孙仲康,郭福成,冯道旺,等.单站无源定位跟踪技术[M].北京:国防工业出版社,2008:114-115. SUN ZHONGKANG,GUO FUCHENG,FENG DAO WANG,et al.Passive location and tracking technology by single observer[M].Beijing:National Defense Industry Press,2008:114-115.(in Chinese)
Abtract:In passive location system,the state model was set up as a airborne single observer moving emitter.The observation model was formed on the base of measuring azimuth angle and its changing rate,and the parameter of Doppler frequency changing rate was introduced.On counter of the instability and low precision in the passive location system with the frequently-used“Extended Kalman Filter”(EKF),“modified function matrix”was calculated,and“Modified Gain EKF”(MGEKF)was adopted.The result of simulation indicated that its precision was higher and its convergence speed was faster.
Tracking Algorithm of Airborne Single Observer to Moving Target Passive Locationn
LI Bing-rong1a,MA Qiang1b,WANG Xin-xin2
(1.Naval Aeronautica and Astronautical University a.Department of Electronic and Information Engineering; b.Department of Training,Yantai Shandong 264001,China; 2.School of Opto-Electronic Information,Yantai University,Yantai Shandong 264005,China)
single observer;airborne;moving emitter;passive location;MGEKF
TN971.+3
A
1673-1522(2014)01-0014-05
10.7682/j.issn.1673-1522.2014.01.004
2013-10-14;
2013-12-10
航空科学基金资助项目(20105584004);泰山学者建设工程专项经费资助项目
李炳荣(1967-),男,副教授,硕士。
