交互多模型PHD滤波跟踪多目标方法
2014-07-07田淑荣孙校书尹付梅张宁
田淑荣,孙校书,尹付梅,张宁
(海军航空工程学院a.基础部;b.科研部;c.训练部,山东烟台264001)
交互多模型PHD滤波跟踪多目标方法
田淑荣a,孙校书b,尹付梅a,张宁c
(海军航空工程学院a.基础部;b.科研部;c.训练部,山东烟台264001)
在机动多目标跟踪问题中,目标数未知或随时间而变化,概率假设密度(PHD)滤波可以在每一时间步估计多目标状态和目标数,但单模型方法不能给出精确的估计。提出了一种交互多模型PHD滤波方法,建立多模型描述多目标运动方式,利用PHD滤波结合多模型跟踪目标运动轨迹。同时,给出了多传感器交互多模型PHD滤波方法,以提高目标跟踪精度。
多目标跟踪;概率假设密度滤波;交互多模型;粒子滤波
多目标跟踪是利用传感器提供的观测值来估计多目标的状态的,由于在监管区域内目标的即时出现和即时消失,可能引起目标数随时间变化。在各时间步,传感器可能以小于1的检测概率提供目标的观测值,也可能提供的是噪声。这就涉及到了集值估计问题,可以用随机有限集建模[1-2]。
概率假设密度(PHD)滤波是基于随机有限集的可行的跟踪多目标方法。通过计算PHD,可以同时估计目标数以及每个目标的状态[3-5]。利用粒子滤波,可以把PHD滤波应用于非线性非高斯问题[6-10]。在机动目标跟踪问题中,由于目标可能改变运动方式,因而运动模型变化的检测和跟踪对于获得正确的多目标状态估计至关重要。对于这类问题,多模型方法可以解决[11],可以利用交互多模型(IMM)PHD粒子滤波跟踪机动多目标。
1 PHD滤波
令γk(xk)表示在k时间步瞬时出现的目标的PHD,bk|k-1(xk|xk-1)表示衍生目标的PHD,fk|k-1(xk|xk-1)为单个目标的转移概率密度,Ps(xk-1)为目标存活概率,gk(zk|xk)是单个目标的似然函数,ck为杂波概率密度,λk为杂波点的泊松平均数,pd为检测概率,Dk-1|k-1(xk-1|Z1:k-1)为k-1时间步的PHD。PHD的预测和更新由下式给出:
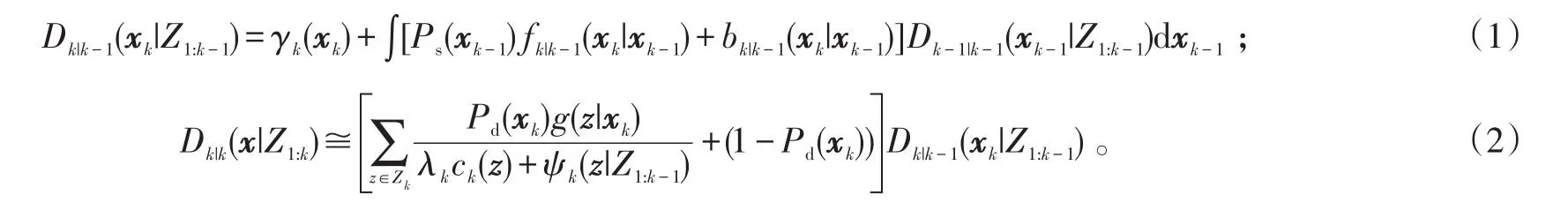
式(1)、(2)中,
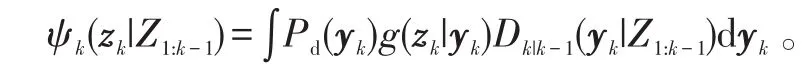
目标数的期望值为
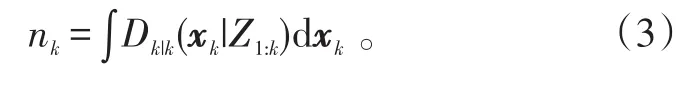
2 IMMPHD滤波
2.1 IMMPHD滤波
假设Nm为运动模型数。在时间步k,运动模型的转移概率为fk|k-1(rk=u|rk-1=v)=hvu,u=1,2,…,Nm,IMMPHDDk|k(xk,rk=u|Z1:k)是依赖于模型的。
IMMPHD滤波过程如下。
在第k(k>1)时间步。
1)混合:
D˜k|k-1(xk-1,rk=u|Z1:k-1)=
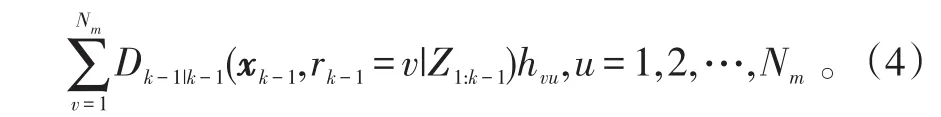
2)预测:
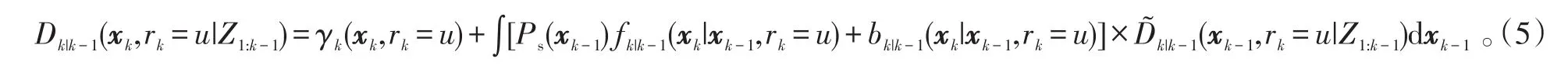
3)更新:
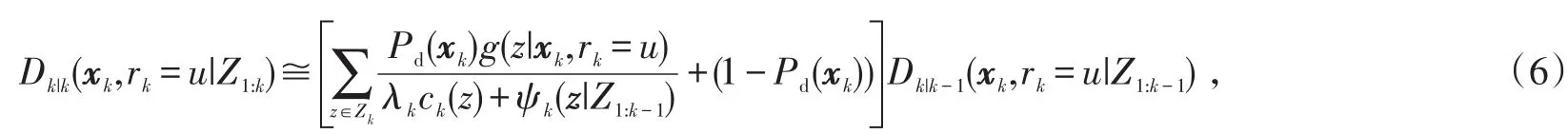
式中,
ψk(z|Zk-1)=∫Pd(xk)g(z|xk,rk=u)Dk|k-1(xk,rk=u|Z1:k-1)dxk。
目标数的期望为
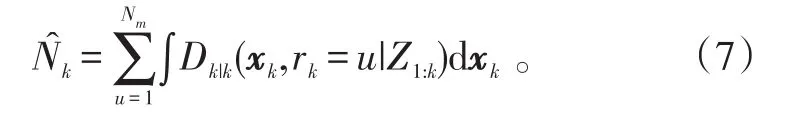
2.2 多传感器IMMPHD粒子滤波
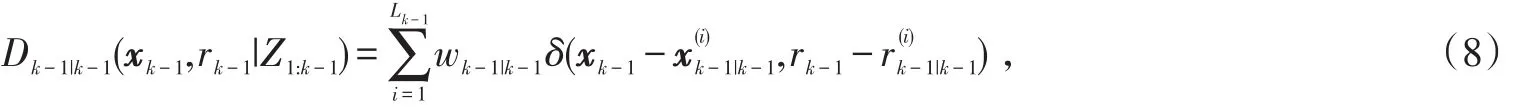
式中,δ(·)为Dirac Delta函数。
在第k(k>1)时间步。
1)混合:
对于i=1,2,…,Lk-1,式中,ρk(rk|rk-1)为指定的模型转移质量函数。
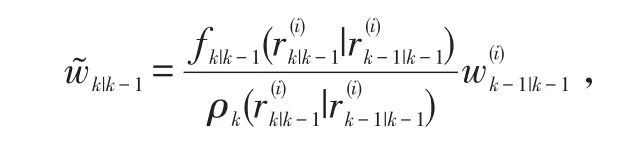
2)预测:
对于i=1,2,…,Lk-1,
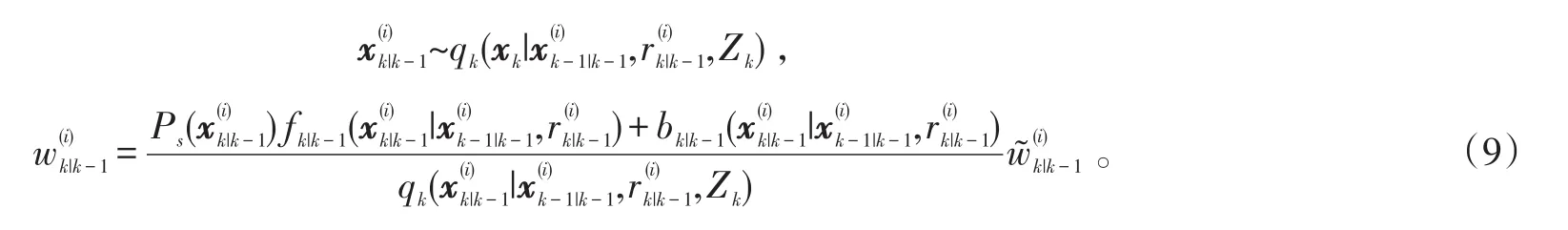
对于i=Lk-1+1,…,Lk-1+Jk,新生目标的粒子
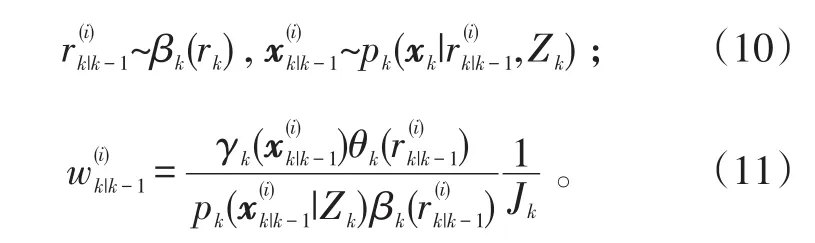
式(10)、(11)中:γk(·)和θk(·)为目标出现的状态密度和模型质量函数,pk(·)和βk(·)为相应的密度和质量函数。
3)更新:
对于i=1,2,…,Lk-1+Jk,以及由ns个传感器获得的观测Zk,1,Zk,2,…,Zk,ns,
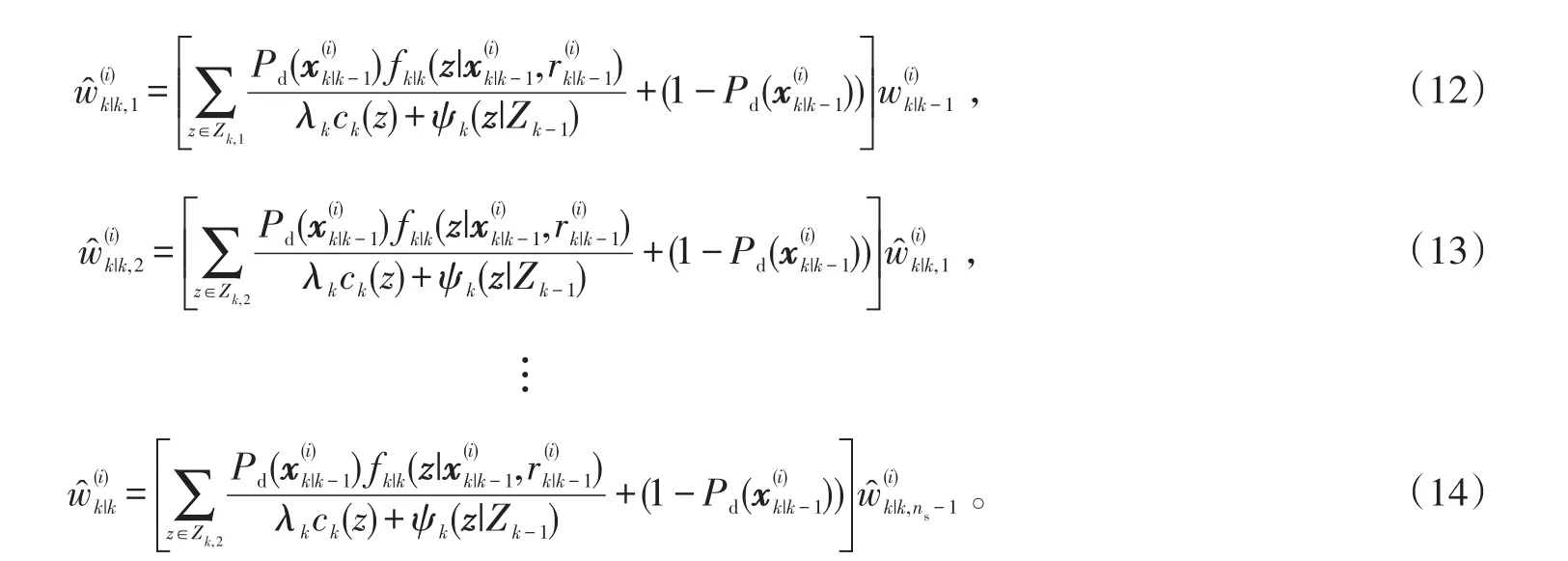
得到期望目标数为

目标数的估计值为N^k=round(nk)。应用标准分类技术可从粒子中提取出N^k个目标的状态估计。
3 仿真实验
一个二维区域内有3个机动目标,初始状态为(-30,0.32,10,0)T、(20,0,25,0.4)T和(-10,0.1,20,0.2)T,分别在时间步k=1、k=3和k=7进入区域,检测概率Pd=0.95。
IMMPHD滤波包含两个模型,模型转移概率矩阵
第1个运动模型:

式(16)中:F1是目标转移矩阵v1.k-1是服从正态分布的过程噪声,其均值为零,协方差阵为Q1,
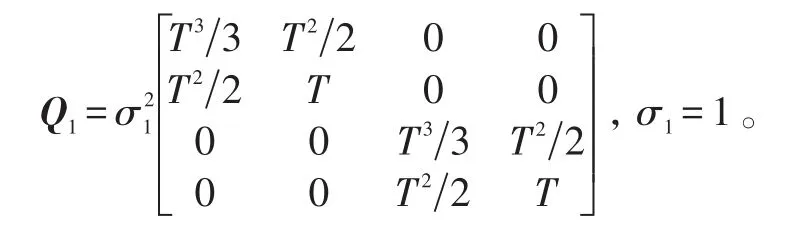
第2个运动模型:

式(17)中:xk=[xk,x˙k,yk,y˙k,αk]T是扩展状态向量,包含k时间步的目标位置[xk,yk]T,目标速度[x˙ky˙k]T和目标弯转率αk;F2是目标转移矩阵,
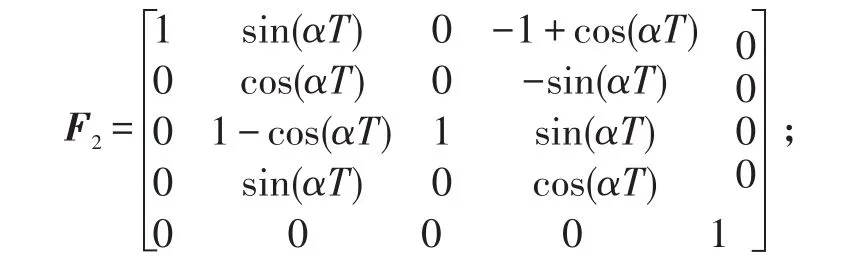
v2.k-1是服从正态分布的过程噪声,其均值为零,协方差阵为Q2,
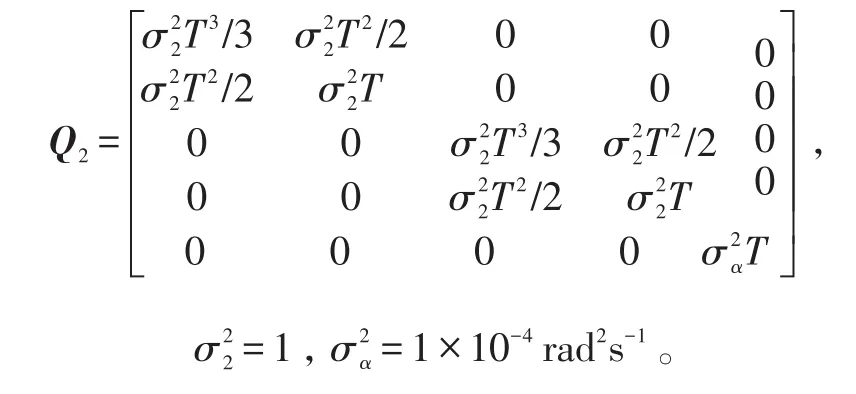
观测模型:zk=(R,θ)T+Vk,R=θ=arctan,2个传感器的位置分别为(xs1,ys1)=(60,60)和(xs2,ys2)=(-20,-20)。采样间隔T=5 s。
杂波在观测空间[0km,50km]×[-π,π]中均匀分布,平均杂波点λk=10。PHD滤波中每个期望目标用1 000个粒子表示,多目标估计误差用Wasserstein距离表示[12]。
目标航迹和目标状态估计如图1所示,目标数和多传感器IMMPHD粒子滤波估计多目标状态的误差如图2所示。由图1、2可以看出,当目标数估计正确时,多目标状态估计误差很小。说明利用多传感器交互多模型PHD滤波方法能在目标机动转换运动模型时正确得到多目标状态估计。
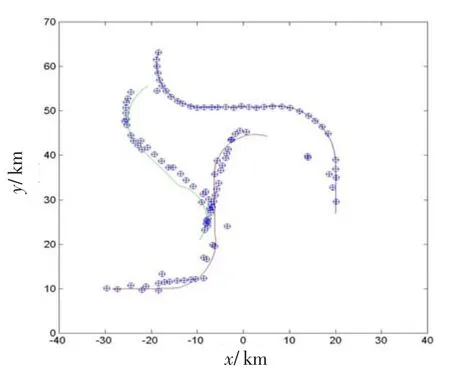
图1 IMMPHD粒子滤波估计目标状态Fig.1 Tracks of targets given by the IMMPHD particle filter
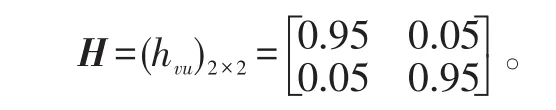
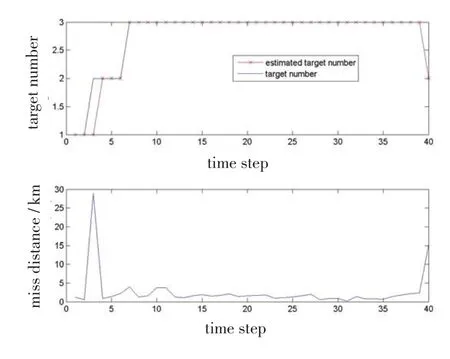
图2 IMMPHD粒子滤波估计目标数及多目标状态误差Fig.2 Multi-target miss distance of the estimates given by the IMMPHD particle filter
4 结论
文中给出了提高机动多目标跟踪精度的交互多模型PHD粒子滤波方法。在2维空间的多目标环境中进行仿真,结果表明该方法能正确跟踪机动多目标。
[1]GOODMAN I,MAHLER R,NGUYEN H.Mathematics of data fusion[M].MA:Kluwer Academic Publishing Co,1997:87-134.
[2]MAHLER R.Statistical multisource-multitarget information fusion[M].Norwood,MA:Artech House,2007:46-60.
[3]MAHLER R,ZAJIC T.Bulk multitarget tracking using a first-order multitarget tracking filter[C]//Kadar I.Signal Processing Sensor Fusion and Target Recognation.XI,Bellingham WA:SPIE,2002:175-186.
[4]MAHLER R.Multitarget bayes filtering via first-order multitarget moments[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(4):1152-1178.
[5]SIDENBLADH H.Multi-target particle filtering for the probability hypothesis density[C]//Proceeding of International Conference Information Fusion.2003:1110-1117.
[6]VO B N,SINGH S,DOUCET A.Sequential Monte Carlo implementation of the PHD filter for multitarget tracking [C]//Proceeding of International Conference Information Fusion.2003:792-799.
[7]VO B N,SINGH S,DOUCET A.Sequential Monte Carlo methods for multitarget filtering with random finite sets [J].IEEE Transactions on Aerospace and Electronic Systems,2005,41(4):1224-1245.
[8]TOBIAS M,LANTERMAN A D.A probability hypothesis density-based multitarget tracker using multiple bistatic range and velocity measurtments[C]//Proceeding of the 36thSoutheastern Symposium on System Theory.Atlanta,2004:205-209.
[9]田淑荣,王国宏,何友.多目标跟踪的概率假设密度粒子滤波[J].海军航空工程学院学报,2007,22(4):417-420. TIAN SHURONG,WANG GUOHONG,HE YOU.Probability Hypothesis Density(PHD)filter for multi-target tracking[J].Journal of Naval Aeronautical Engineering Institute,2007,22(4):417-420.(in Chinese)
[10]TIAN SHURONG,HE YOU,WANG GUOHONG.PHD filter of multi-target tradking with passive radar observations[C]//International Conference on Signal Processing. 2006:2747-2050.
[11]BAR-SHALOM Y,LI X,KIRUBARAJAN T.Estimation with applications to tracking and navigation[M].New York,NY:Wiley,2001:181-193.
[12]HOFFMAN J,MAHLER R.Multitarget miss distance via optimal assignment[J].IEEE Transactions on Aerospace and Electronic Systems,Man and Cybernetics:Part A,2004,34(3):327-336.
Interactive Multi--Modle PHD Filtrr for Multi--Target Tracking
TIAN Shu-ronga,SUN Xiao-shub,YIN Fu-meia,ZHANG Ningc
(Naval Aeronautical and Astronautical University a.Department of Basic Sciences; b.Department of Scientific Research;c.Department of Training,Yantai Shandong 264001,China)
In mameuvering multiple-target tracking problem,the number of targets was unknown or varied with time,probability hypothesis density(PHD)filter can be used to estimate the multi-target state and the number at each time step,but single model method may not provide accurate estimates.In this paper,a interactive multiple model PHD filter was proposed,and then multiple sensor interactive multiple model PHD filter was proposed to improve the tracking of multiple maneuvering targets.PHD particle filter implementation was used to perform the proposed method consisting of multiple mameuvering targets.
multi-target tracking;PHD filter;interactive multi-model;particle filter
TN953
A
1673-1522(2014)01-0029-04
10.7682/j.issn.1673-1522.2014.01.007
2013-10-10;
2013-11-20
2013年度海军航空工程学院基础研究基金资助项目
田淑荣(1970-),女,副教授,博士。
